Undetected infectives in the Covid-19 pandemic

Abstract

Objectives

Epidemiological investigations and mathematical models have revealed that the rapid diffusion of Covid-19 can mostly be attributed to undetected infective individuals who continue to circulate and spread the disease: finding their number would be of great importance in the control of the epidemic.

Methods

The dynamics of an infection can be described by the SIR model, which divides the population into susceptible $\left(S\right)$, infective $\left(\mathit{I}\right)$, and removed $\left(\mathit{R}\right)$ subjects. In particular, we exploited the Kermack-McKendrick epidemic model, which can be applied when the population is much larger than the fraction of infected subjects.

Results

We proved that the fraction of undetected infectives, compared to the total number of infected subjects, is given by $1-\frac{1}{R_0}$, where $R_0$ is the basic reproduction number. The mean value $R_0=2.10\left(2.09-2.11\right)$ for the Covid-19 epidemic in three Italian regions yielded a percentage of undetected infectives of 52.4% (52.2%–52.6%) compared to the total number of infectives.

Conclusions

Our results, straightforwardly obtained from the SIR model, highlight the role of undetected carriers in the transmission and spread of the SARS-CoV-2 infection. Such evidence strongly recommends careful monitoring of the infective population and ongoing adjustment of preventive measures for disease control until a vaccine becomes available for most of the population.

Introduction

A critical issue in the control of an epidemic is to know the exact number of infective subjects. Current estimates of SARS-CoV-2 infection are significantly hampered by the difficulty to perform large-scale diagnostic tests, despite the current awareness that the spread of the Covid-19 pandemic is mostly caused by undetected carriers.

The speed at which an epidemic grows cannot be explained if we only consider the number of recorded infected patients who, supposedly, are immediately removed from the circulating population by hospitalization or isolation at home.

Undetected infectives can be classified into two categories: 1) paucisymptomatic or asymptomatic individuals, who never develop overt symptoms during the course of infection; 2) presymptomatic subjects, who will eventually develop symptoms. Undetected infectives are largely responsible for the rapid increase of the epidemic. To reliably detect their presence, it would be necessary to test the entire population and not just the symptomatic cases.

The dynamics of an epidemic can be described by an epidemiological model known as the SIR model, which divides the whole population into three classes of subjects: susceptible $\left(S\right)$, infective $\left(I\right)$, and removed $\left(R\right)$ individuals. Kermack and McKendrick (1933) developed a SIR model for the study of epidemics in populations much larger than the infected fraction. Under this assumption, which is fully verified in the Covid-19 epidemic, we proved that the total number of infectives, when an epidemic occurs, is approximately $R_0\cdot R$, where $R_0>1$ is the basic reproduction number of the infection and $R$ is the number of infectives who have been removed because of recovery, isolation, hospitalization or death. The number of undetected infectives is then $\left(R_0-1\right)\cdot R$. The fractions of removed and undetected infectives, in comparison to the total number of infectives, are $\frac{1}{R_0}$ and $1-\frac{1}{R_0}$, respectively.

By applying the model described above to the data available on the Covid-19 epidemic in Italy, we calculated that the mean value of the basic reproduction number in three Italian regions (Lombardy, Emilia-Romagna, and Sardinia) was $R_0=2.10$ (95% confidence interval, 2.09–2.11). Consequently, the number of undetected cases turned out to be about $R_0-1=1.1$ times the number of removed cases. More specifically, we found that the percentage of undetected infectives was about $1-\frac{1}{R_0}=52.4\%$(95% confidence interval, 52.2%–52.6%) of the total number of infectives.

Previous investigations found that the percentages of asymptomatic infectives (i.e., subjects without fever, cough, or any other symptoms) were: 43.2% (32.2%–54.7%) in Vo’, a small town near Padua in Italy (Lavezzo et al., 2020); 50.5% (46.5%–54.4%) onboard the Diamond Princess cruise ship in Yokohama, Japan (Mizumoto et al., 2020); 47% (38%–56%) in mainland China (Li et al., 2020b) and 52.0% (including paucisymptomatic infectives) in a large sample (64,660 subjects) of the Italian population (Italian National Institute of Statistics, 2020).

The data provided by the Italian Ministry of Health and Civil Protection Department (2020) up to the 3rd of June 2020 reported about 233,800 removed cases in Italy, including either patients hospitalized or isolated at home or recovered or dead. Based on the result found in the present study, the total number of paucisymptomatic, asymptomatic, and presymptomatic infectives had to be almost 491,000 up to that date. This means that 257,200 individuals were not diagnosed as infected, although they continued to circulate and spread the virus.

This study confirms that undetected infectives can be considered the key culprits for the rapid spread of SARS-CoV-2 within the population. Consequently, interventions to control the infection will need to be maintained until the complete disappearance of the epidemic.

Methods

In the SIR epidemic model, the population is divided into three distinct classes (Murray, 2002): the susceptible subjects, $S$, who can catch the disease; the undetected infectives, $I$, who have the disease and can transmit it; and the removed infected subjects, $R$, namely those with a laboratory diagnosis who are either hospitalized, isolated at home, dead or recovered.

We assume that all the individuals diagnosed as infected – either by nasopharyngeal swab or serological test – are immediately isolated, thus passing from the class of infectives $I$ to that of the removed infectives $R$. On the contrary, the infected subjects without a positive diagnosis are classified as undetected infectives $\left(U\right)$, who are either still infective $\left(I\right)$ or infected but no longer contagious ($U_0$). The total number of undetected infectives $U$ is then given by: $U=I+U_0$.

At any time $t$, the total number of infected subjects $I_{tot}\left(t\right)$ is the sum of the number of removed infectives $R\left(t\right)$ and undetected infectives $U\left(t\right)$: $I_{tot}\left(t\right)=R\left(t\right)+U\left(t\right)$. As discussed in the Introduction, the undetected infective individuals can be asymptomatic, paucisymptomatic, or presymptomatic.

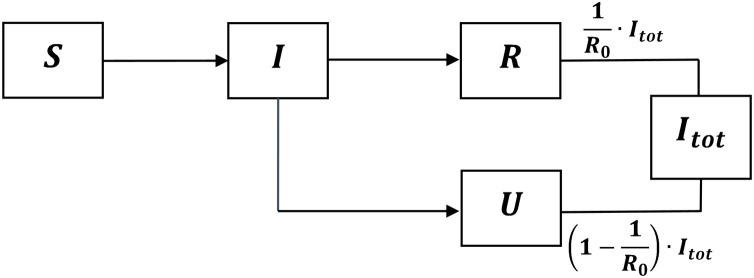
The progression of an individual from the susceptible compartment $S$ to the total infected class $I_{tot}$ is represented by the scheme in Figure 1 .

Figure 1.

Scheme representing the progression of an individual from the susceptible compartment $S$ to the total infected class $I_{tot}$. The fractions of $I_{tot}$ in the $R$ and $U$ compartments are $\frac{1}{R_0}$ and $1-\frac{1}{R_0}$, respectively.

If $S\left(t\right)$ is the number of susceptible individuals at time $t$ and $N$ is the size of the population, the total number of infected subjects $I_{tot}\left(t\right)$ turns out to be

$$I_{tot}\left(t\right)=N-S\left(t\right)$$

By manipulating the differential equations which define the SIR model (Appendix A) and assuming that the initial number $S_0$ of susceptible individuals is close to $N$, i.e., $S_0\cong N$, one obtains

$$\frac{dS}{dR}\cong -\frac{R_0}{N}\cdot S\Rightarrow S\left(t\right)\cong N\cdot e^{-R_0\cdot R\left(t\right)/N}$$

where $R_0$ is the basic reproduction number (discussed in Appendix B). Under the assumption $R_0\cdot R\left(t\right)/N\ll 1$ (a condition which is certainly verified if the population size is much larger than the number of infected subjects), we can approximate $S\left(t\right)$ in the following form:

$$S\left(t\right)\cong N\cdot \left[1-\frac{R_0}{N}\cdot R\left(t\right)+\frac{1}{2}{\left(\frac{R_0}{N}\right)}^2\cdot R{\left(t\right)}^2\right]$$

The total number of infected subjects $I_{tot}\left(t\right)$ at time $t$ then becomes

$$I_{tot}\left(t\right)=N-S\left(t\right)\cong R_0\cdot R\left(t\right)\cdot \left[1-\frac{R_0}{2N}\cdot R\left(t\right)\right]$$

while the undetected infectives $U\left(t\right)$ at time $t$ turn out to be

$$U\left(t\right)=I_{tot}\left(t\right)-R\left(t\right)\cong \left(R_0-1\right)\cdot R\left(t\right)\cdot \left[1-\frac{R_0^2}{2\left(R_0-1\right)N}\cdot R\left(t\right)\right]$$

The ratio between the removed infected subjects $R\left(t\right)$ and $I_{tot}\left(t\right)$ at time $t$ is

$$\frac{R\left(t\right)}{I_{tot}\left(t\right)}\cong \frac{1}{R_0\cdot \left[1-\frac{R_0}{2N}\cdot R\left(t\right)\right]}$$

while the ratio between the undetected infectives $U\left(t\right)$ and $I_{tot}\left(t\right)$ at time $t$ is

$$\frac{U\left(t\right)}{I_{tot}\left(t\right)}=1-\frac{R\left(t\right)}{I_{tot}\left(t\right)}\cong \frac{R_0-1}{R_0}\cdot \frac{1-\frac{R_0^2}{2\left(R_0-1\right)N}\cdot R\left(t\right)}{1-\frac{R_0}{2N}\cdot R\left(t\right)}$$

Being $R_0\cdot R\left(t\right)/N\ll 1$, the previous four equations can be approximated as

$$\begin{gathered} I_{tot}\left(t\right)\cong R_0\cdot R\left(t\right),U\left(t\right)\cong \left(R_0-1\right)\cdot R\left(t\right), \\ \frac{R\left(t\right)}{I_{tot}\left(t\right)}\cong \frac{1}{R_0},\frac{U\left(t\right)}{I_{tot}\left(t\right)}\cong 1-\frac{1}{R_0} \end{gathered}$$

These results are obtained under the assumption $S_0\cong N$, which implies $R_0>1$, i.e., that an epidemic ensues.

The fraction of undetected infectives $U$, compared to the total infectives $I_{tot}$, has been derived straightforwardly from the SIR epidemic model and only depends on the basic reproduction number $R_0$.

Appendix A provides further details on the SIR model, Appendix B shows how the evaluation of the basic reproduction number $R_0$ was performed, Appendix C presents the numerical fit of the data, Appendix D shows how the effective reproduction number $R_{\text{eff}}\left(t\right)$ was computed, Appendix E describes the evaluation of the constants of the fit from the data at the peak of new infectives and Appendix F shows the application of the model to stratified groups.

Results

The data provided by the Italian Ministry of Health and Civil Protection Department (2020), updated to the 3rd of June 2020, were fitted for three Italian regions using a specific code written with Wolfram Mathematica 12.1 (Wolfram, 2020) and based on the Kermack-McKendrick model (Kermack and McKendrick, 1933).

Lombardy, in the north of Italy, has been the region with the highest number of Covid-19 infections, followed by Emilia-Romagna (at the second place from the 29th of February to the 24th of April, at the third place in the other periods of the epidemic). On the contrary, the Island of Sardinia, in the South of Italy, was one of the regions with the lowest number of documented Covid-19 infections and deaths. The population size $N$ in these regions, updated to the 1st of January 2019, were: Lombardy N = 10,060,574, Emilia-Romagna N = 4,459,477, Sardinia N = 1,639,591 (data from the Italian National Institute of Statistics).

In these three Italian regions, our epidemiological model yielded the mean value $R_0=2.10\left(2.09-2.11\right)$ for the basic reproduction number $R_0$ (Appendix B).

Time $t$ was expressed in days since $t_0$ ($t=0$), the day before the date of the first diagnosed patient: 19th of February in Lombardy, 20th of February in Emilia-Romagna, and 2nd of March in Sardinia.

At any time $t$, the mean percentage of removed infectives $R\left(t\right)$ in comparison to the total number of infectives $I_{tot}\left(t\right)$ was about $\frac{1}{R_0}\cong 47.6\%\left(47.4\%-47.8\%\right)$, while the mean percentage of undetected infectives $U\left(t\right)$ was about $1-\frac{1}{R_0}\cong 52.4\%\left(52.2\%-52.6\%\right)$.

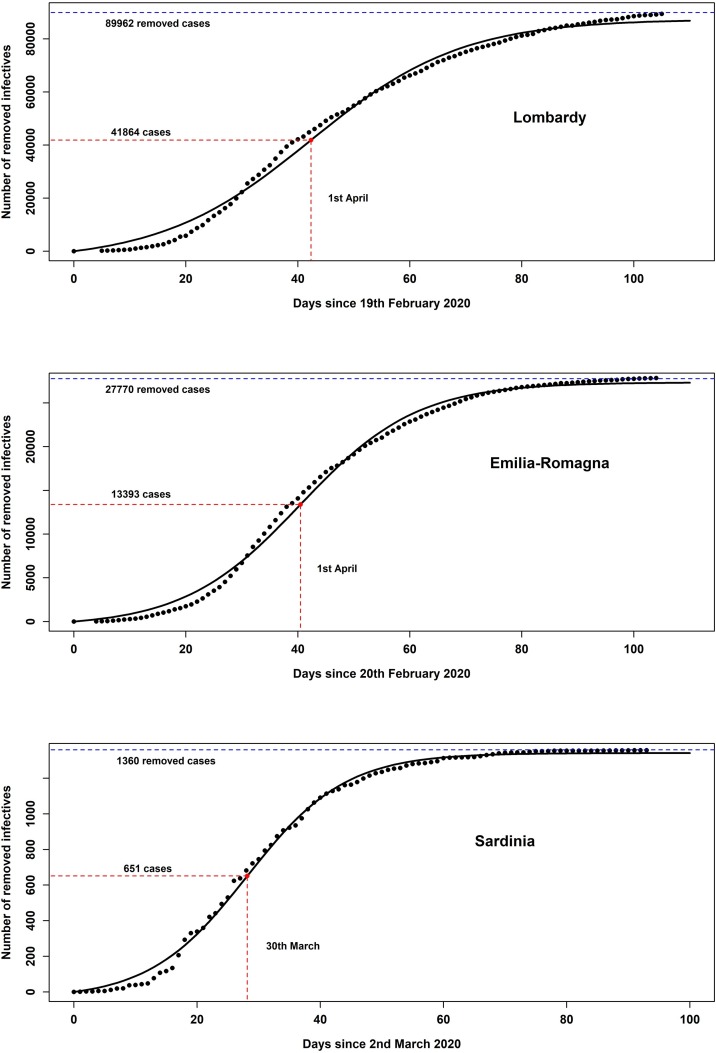
Based on the data provided by the Italian Ministry of Health and Civil Protection Department (2020), Figure 2 represents the number of removed infectives $R\left(t\right)$ in Lombardy, Emilia-Romagna, and Sardinia, fitted by the equation $R\left(t\right)=c_1\cdot \left[\tanh \left(c_{2}t-c_3\right)+\tanh (c_3)\right]$. Further details are discussed in Appendix C.

Figure 2.

The fit of the number of removed infectives $R\left(t\right)$ according to the Kermack-McKendrick model in three Italian regions.

In Appendix D, the Kermack-McKendrick model was also used to compute the effective reproduction number $R_{\text{eff}}\left(t\right)$ and to evaluate the time corresponding to the threshold $R_{\text{eff}}\left(t\right)=1$ at which the epidemic starts to decline.

Table 1 reports the main epidemic parameters of the Covid-19 epidemic in Lombardy, Emilia-Romagna, and Sardinia: the basic reproduction number $R_0$, the final numbers (for $t\to \infty$) of the removed ($R$), undetected ($U$) and total $I_{tot}$ infectives, the percentages $U/I_{tot}$ and $R/I_{tot}$, the day $t_0$ when the epidemic started, the time $t_{\text{peak}}$ (both in days, since $t_0$, and according to calendar date) of the maximum rate $R\text{'}\left(t_{\text{peak}}\right)$ of new cases per day, with the corresponding number of removed infectives $R\left(t_{\text{peak}}\right)$, the constants $c_1$, $c_2$, $c_3$ in the equation $R\left(t\right)=c_1\cdot \left[\tanh \left(c_{2}t-c_3\right)+\tanh (c_3)\right]$, determined by fitting the data on the Covid-19 epidemic with Wolfram Mathematica 12.1 (Wolfram, 2020).

Table 1.

Main epidemic parameters from the fit of the removed infectives $R\left(t\right)$ in Lombardy, Emilia-Romagna, and Sardinia. The 95% confidence intervals are reported between brackets.

Parameters	Lombardy	Emilia-Romagna	Sardinia
$R_0$	2.07 (2.06–2.08)	2.10 (2.09–2.11)	2.13 (2.12–2.14)
$R\left(t\to \infty \right)$	87472 (84982–89962)	27348 (26926–27770)	1341 (1323–1360)
$U\left(t\to \infty \right)$	92036 (88976–95097)	29619 (29022–30216)	1508 (1479–1537)
$I_{tot}\left(t\to \infty \right)$	179508 (173957–185059)	56967 (55948–57986)	2849 (2802–2897)
$U/I_{tot}$ (%)	51.3% (51.1%–51.4%)	52.0% (51.9%–52.1%)	52.9% (52.8%–53.1%)
$R/I_{tot}$ (%)	48.7% (48.6%–48.9%)	48.0% (47.9%–48.1%)	47.1% (46.9%–47.2%)
$t_0$ (date)	19th February 2020	20th February 2020	2nd March 2020
$t_{\text{peak}}$ (days)	42.3 (37.2–47.5)	40.5 (36.7–44.2)	28.2 (25.8–30.5)
$t_{\text{peak}}$ (date)	1 Apr (27 Mar–7 Apr)	1 Apr (28 Mar–4 Apr)	30 Mar (28 Mar–2 Apr)
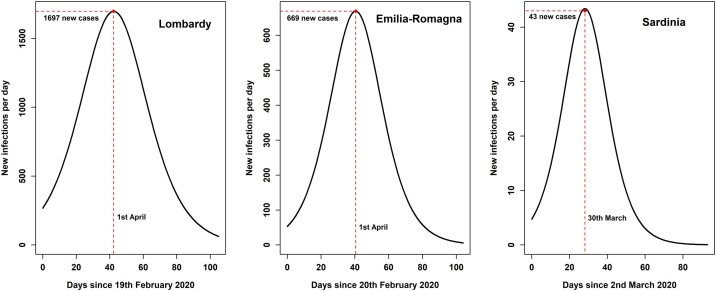
$R\text{'}\left(t_{\text{peak}}\right)$	1697 (1560–1835)	669 (631–708)	43 (41–46)
$R\left(t_{\text{peak}}\right)$	41864 (40308–43421)	13393 (13135–13650)	651 (639–663)
$c_1$	4.561 (4.467–4.654)∙104	1.396 (1.379–1.412)∙104	6.901 (6.837–6.964)∙102
$c_2$	0.037 (0.035 – 0.039)	0.048 (0.046 – 0.050)	0.063 (0.060 – 0.066)
$c_3$	1.576 (1.478–1.673)	1.942 (1.852–2.032)	1.772 (1.694–1.850)

The validity of our model was tested by determining the constants $c_1$, $c_2$, $c_3$ of the fit from the data on $R\left(t_{\text{peak}}\right)$ and $R\text{'}\left(t_{\text{peak}}\right)$, as discussed in Appendix E. The results obtained only differ by a maximum of 3% from the values in Table 1, thereby confirming that our model provides reliable estimates of the main epidemic parameters.

Figure 3 shows the number of newly recorded infectives per day in Lombardy, Emilia-Romagna, and Sardinia. These curves plot the equation $\frac{dR}{dt}=c_1\cdot c_2\cdot {\left[\text{sech}\left(c_{2}t-c_3\right)\right]}^2$ (Appendix C), which yields the rate of newly removed infectives in the Kermack-McKendrick model.

Figure 3.

Rate $\frac{dR}{dt}$ of newly removed infectives per day according to the Kermack-McKendrick model in three Italian regions.

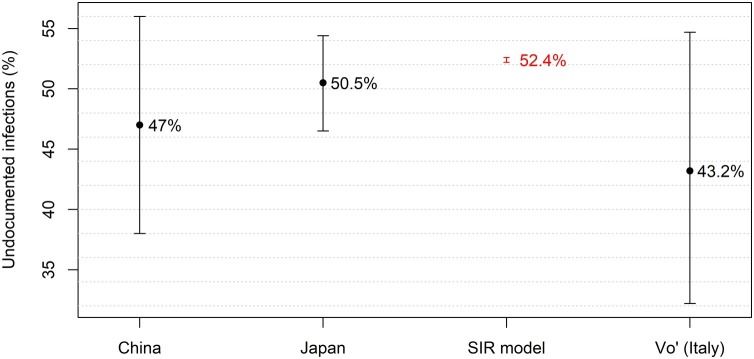
Figure 4 compares the percentages of asymptomatic infectives found in three previous investigations, conducted in Vo’ (Lavezzo et al., 2020), Japan (Mizumoto et al., 2020), and China (Li et al., 2020b), with the percentage of undetected infectives in Lombardy, Emilia-Romagna and Sardinia obtained in this study through the SIR model.

Figure 4.

Comparison between the percentage of undetected infectives obtained using the SIR model and the percentages of asymptomatic infectives in three previous investigations conducted in China, Japan, and Vo' (Italy). The error bars represent the 95% confidence intervals.

The serological investigation conducted in Italy on 64,660 subjects from the 15th of May to the 15th of July 2020 revealed that the percentage of paucisymptomatic infectives was 24.7% and that of asymptomatic infectives was 27.3%. Therefore, the total percentage of paucisymptomatic and asymptomatic infectives was 52.0%, as discussed in the preliminary report released by the Italian National Institute of Statistics (2020).

The result obtained with the SIR model (shown in Figure 4) seems to be affected by a relatively small error compared to the errors of other studies. The reason is that the 95% confidence interval associated with our finding only represents the uncertainty intrinsic to the mathematical model, excluding the error in the data provided by the Italian Ministry of Health and Civil Protection Department (2020) for removed infectives $R\left(t\right)$ at time $t$. These data were probably underestimated because of the difficulty to administer swabs or serological tests to all the suspect cases or even to subjects with overt symptoms. However, we only considered the errors associated with the statistical goodness of fit in our model, being unable to evaluate the uncertainty of the data on removed infectives.

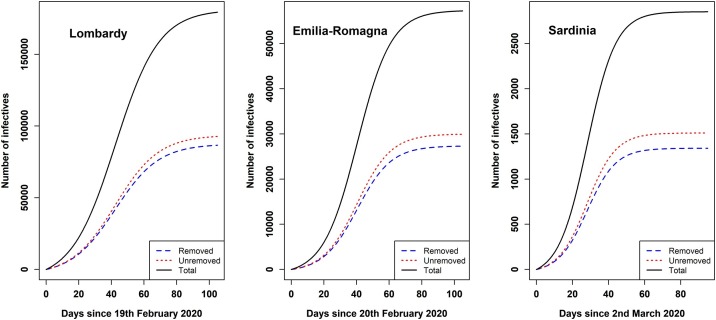
Figure 5 shows the plots against time $t$ of the number of removed, undetected and total infectives in three Italian regions according to the Kermack-McKendrick model, i.e., $R\left(t\right)=c_1\cdot \left[\tanh \left(c_{2}t-c_3\right)+\tanh (c_3)\right]$ (with $c_1$, $c_2$, $c_3$ given in Table 1), $U\left(t\right)=\left(R_0-1\right)\cdot R\left(t\right)$ and $I_{tot}\left(t\right)=R_0\cdot R\left(t\right)$, respectively.

Figure 5.

Plots against time $t$ of the number of removed, undetected and total infectives in Lombardy, Emilia-Romagna, and Sardinia according to the Kermack-McKendrick model.

The assumption that the population size must be larger than the number of infected subjects corresponds to an approximated relative error $\frac{R_0\cdot R\left(t\right)}{2N}$ on the undetected fraction of infectives, i.e., a percent error lower than 0.9% in Lombardy, 0.6% in Emilia-Romagna, and 0.1% in Sardinia.

Our model can be applied to a sample of infected individuals stratified into two groups by a specific characteristic, e.g., age or gender (Appendix F). The stratification of the undetected infectives $U$ in the two groups turns out to approach that of the whole sample of infected subjects $I_{tot}$, i.e., $\frac{U_1}{U_2}\cong \frac{I_{tot;1}}{I_{tot;2}}$. This conclusion was confirmed by exploiting the data of the investigation conducted in Vo' (Lavezzo et al., 2020).

Discussion

The speed at which an infection spreads is strongly influenced by the number of undetected infected individuals who contribute to disseminate the virus without being diagnosed as positive. This study proved that in any epidemic the fraction of undetected infectives, compared to the total number of infections, is given by the approximated expression $1-\frac{1}{R_0}$, which only depends on the basic reproduction number $R_0$.

The analytical expression of $R_0$ found in Appendix B was exploited to compute the basic reproduction number in three Italian regions (Lombardy, Emilia-Romagna, and Sardinia); the corresponding mean value $R_0=2.10$ (95% confidence interval, 2.09–2.11) overlaps well with the result $R_0=2.2\left(1.4-3.9\right)$ found in China (Li et al., 2020a) and the result $R_0=$ 2.28 (2.06–2.52) obtained in Japan from the data collected onboard a cruise ship (Zhanga et al., 2020).

In Appendix D, the Kermack-McKendrick model was also used to compute the effective reproduction number $R_{\text{eff}}\left(t\right)$, as previously defined, e.g., by Nishiura and Chowell (2009).

By exploiting the aforesaid mean value of $R_0$, we found that the percentage of undetected infectives was $1-\frac{1}{R_0}\cong 52.4\%$ (95% confidence interval, 52.2%–52.6%) of the total infectives.

The assumption that the population size must be larger than the number of infected subjects corresponds to a percent error lower than 1% on the undetected fraction of infectives.

As shown in Figure 4, the percentage of undetected infectives obtained in this study overlaps well with the percentages of asymptomatic infectives found in previous investigations (Lavezzo et al., 2020, Mizumoto et al., 2020, Li et al., 2020b), confirming that the fraction of undetected infectives is considerable and is likely to have a strong influence on the dynamics of the epidemic.

In a study conducted in Vo’ (Lavezzo et al., 2020), a small town in Veneto (Italy), most inhabitants were tested through nasopharyngeal swabs in two consecutive surveys; the mean percentage of asymptomatic infectives corresponded to 43.2% (32.2%–54.7%) of the total SARS-CoV-2 infections. Notably, the nasopharyngeal swabs performed in this study showed no statistically significant differences between the viral load of symptomatic and asymptomatic infections. Moreover, the viral load tended to peak in the large majority of participants around the day of symptom onset, suggesting an essential role for presymptomatic transmission in the spread of the virus. Therefore, both asymptomatic and presymptomatic transmission represent a major threat to epidemiologic control and containment of the infection (Lavezzo et al., 2020).

An investigation performed on the passengers of the Diamond Princess (Mizumoto et al., 2020), a cruise ship in Yokohama (Japan), revealed that from the start of the epidemic the percentage of asymptomatic infectives on board the ship was 50.5% (46.5%–54.4%) of the total infectives.

One of the first studies (Li et al., 2020b) to reveal the crucial role of undetected infections in the Covid-19 pandemic estimated the undetected fraction of infectives on the basis of a mathematical model connecting mobility data and observations of reported infections within China. The percentage of undetected infectives turned out to be $U=86.2\%\left(81.6\%–89.8\%\right)$ of the total number of positive cases. However, in this study the transmission rate of undetected infectives was assumed to be $\mu =55\%\left(46\%-62\%\right)$ of the transmission rate of symptomatic infectives. On the contrary, we assumed that all infected subjects – with or without symptoms – may present an elevated viral load and transmit the virus at the same rate, as confirmed by the investigation in Vo’ (Lavezzo et al., 2020) and the systematic literature search conducted by Walsh et al. (2020). Under this assumption, the effective percentage $U_{\text{eff}}$ of undetected infectives is given by $U_{\text{eff}}=\mu \cdot U=47\%\left(38\%-56\%\right).$

Another study (Yusef et al., 2020) investigated 350 attendees of a wedding in Jordan, 76 of whom tested positive for SARS-CoV-2. Among them, 36 individuals were asymptomatic, i.e., 47.4% (35.8%–59.2%) of the total number of infected subjects.

The studies by Lavezzo et al. (2020), Mizumoto et al. (2020) and Yusef et al. (2020) were based on laboratory tests performed in small communities (the inhabitants of Vo’ in Italy, the passengers of a cruise ship in Japan, and the attendees of a wedding in Jordan, respectively) where the Covid-19 infection had spread. On the contrary, the study in China (Li et al., 2020b) was based on a mathematical model comparing mobility data and infection diffusion in mainland China after the start of the Covid-19 epidemic.

A serological investigation in the Italian population conducted by the Italian National Institute of Statistics (2020) on 64,660 subjects revealed that the percentage of paucisymptomatic and asymptomatic infectives up to mid-July 2020 was 52.0%.

A Review by Oran and Topol (2020) of the available evidence on asymptomatic SARS-CoV-2 infectives found that asymptomatic subjects accounted for approximately 40%–45% of the total number of infections and could transmit the virus to others. The authors of the Review also pointed out that the high frequency of asymptomatic infections could at least partly explain the rapid spread of the virus, since infected subjects who feel and look well are likely to have more social interaction compared to symptomatic infectives.

The results obtained in the previous investigations (Lavezzo et al., 2020, Mizumoto et al., 2020, Yusef et al., 2020, Oran and Topol, 2020) concerned asymptomatic infected subjects, while the results found in our study included all the undetected infectives, both asymptomatic subjects, and paucisymptomatic or presymptomatic individuals. This can explain why the percentages of asymptomatic infected subjects in those studies turned out to be a bit lower than the percentage we found for all the undetected infectives.

The 95% confidence intervals of the epidemiological parameters reported in Table 1 were only associated with the error intrinsic to the mathematical model used in this study, while the uncertainty of the data concerning removed infectives was not included, although the recorded positive cases were probably underestimated as a consequence of the low efficiency in administering swabs and serological tests to the population in most Italian regions.

Conclusions

Our derivation of the percentage of undetected infectives only relied on the SIR model, a cornerstone in the study of infectious disease dynamics. Despite its simplicity, the SIR model describes the global dynamics of an epidemic and allows for the evaluation of several epidemiological parameters. However, more complex and realistic generalizations of the SIR model could be introduced to further refine and improve the true picture of an epidemic.

The general expression of the percentage of undetected infectives found in this study only requires knowledge of the basic reproduction number $R_0$. Other methods involve numerous variables in order to achieve a more accurate description of an epidemic. However, these methods require specific assumptions about unknown parameters of the underlying mathematical framework.

The main conclusion which can be drawn from the results obtained in this study is that undetected infections play a crucial role in the transmission of SARS-CoV-2. The high percentage of undetected infections poses a major challenge for the control of Covid-19 and highlights the necessity to carefully monitor and adjust social distancing and other preventive measures until a sufficiently high vaccination rate is reached.

Authors’ contributions

The authors contributed equally to the article.

Conflicts of interest

None declare.

Funding

None declare.

Ethical approval

Not applicable.

Appendix A. Supplementary data

The following is Supplementary data to this article: