Abstract
Solution-processed quantum dot (QD) lasers are one of the holy grails of nanoscience. They are not yet commercialized because the lasing threshold is too high: one needs >1 exciton per QD, which is difficult to achieve because of fast nonradiative Auger recombination. The threshold can, however, be reduced by electronic doping of the QDs, which decreases the absorption near the band-edge, such that the stimulated emission (SE) can easily outcompete absorption. Here, we show that by electrochemically doping films of CdSe/CdS/ZnS QDs, we achieve quantitative control over the gain threshold. We obtain stable and reversible doping of more than two electrons per QD. We quantify the gain threshold and the charge carrier dynamics using ultrafast spectroelectrochemistry and achieve quantitative agreement between experiments and theory, including a vanishingly low gain threshold for doubly doped QDs. Over a range of wavelengths with appreciable gain coefficients, the gain thresholds reach record-low values of ∼1 × 10–5 excitons per QD. These results demonstrate a high level of control over the gain threshold in doped QD solids, opening a new route for the creation of cheap, solution-processable, low-threshold QD lasers.
Keywords: ultrafast spectroelectrochemistry, quantum-dots, doping, optical gain, electrochemistry, transient absorption spectroscopy
Introduction
Colloidal semiconductor quantum dots (QDs) are attractive materials for solution-processable and color-tunable lasers.1−4 Additionally, as they have discrete electronic states with finite degeneracy, QDs are ideal systems to achieve low threshold optical gain, promising a reduction of the threshold current in lasers. However, the larger-than-unity degeneracy of the conduction and valence-band levels implies that multiexcitons are required to achieve population inversion in QDs, i.e., for stimulated emission (SE) to outcompete absorption. Because Auger recombination is efficient in QDs,5 multiexcitons have short lifetimes, typically <100 ps, implying that it is difficult to achieve/maintain a population sufficient for gain. Additionally, ultrafast charge-carrier trapping can compete with the buildup of optical gain when the trapping rates are similar to the time for the QDs to achieve population inversion.6
Prolonged Auger lifetimes up to a nanosecond have been achieved in QD heterostructures to overcome these limitations.7,8 Moreover, in CdSe QDs, the band-edge hole degeneracy can be decreased in the presence of strain,9 reducing the number of excitons needed to achieve population inversion to ∼1. Subsingle-exciton optical gain has been realized in type II heterostructures10 and in HgTe QDs,11 which show a large shift of the SE to wavelengths where there is little absorption, at the cost of lower gain coefficients.
A potentially more controllable method to suppress absorption employs QD charging.12−14 In 2004, pioneering work on electrochemical charging by the group of Guyot-Sionnest showed a reduction in the threshold for amplified stimulated emission (ASE).15 Recently, Wu et al. demonstrated nearly thresholdless optical gain using photochemical doping as a strategy to charge the QDs,7 which when coupled to a distributed feedback grating shows subsingle exciton lasing.16 Although these recent results show the promise of QD charging for lasing, there is limited and only temporary control over the charge density and as a result, thresholdless gain has not been achieved. Electrochemical doping has the advantage that the electrochemical potential can be fixed and held constant over a QD film. When the QDs are sufficiently passivated with stable shells, this results in a stable and homogeneous doping density of the QD film.17,18
In the current work, we seek to get quantitative understanding and control over the gain properties of QD films when doped with electrons. We combined spectroelectrochemistry with ultrafast transient absorption (TA) spectroscopy, characterizing material gain as a function of electrochemical doping density and optical excitation density. We measured the number of photogenerated excitons per QD to produce optical gain as a function of the average number of electrochemically injected electrons into the 1S(e) conduction band state. In a broad wavelength range, we achieve vanishingly low optical gain thresholds (<1 × 10–3 to 1 × 10–5 excitons per QDs). Modeling the effect of state filling, stimulated emission and carrier relaxation on optical gain, we get good agreement between the predicted and experimentally determined gain threshold and gain lifetime as a function of ⟨n1S(e)⟩. This demonstrates that we have quantitative control over the optical gain in these QD solids.
Results and Discussion
We synthesized wurtzite core–shell–shell CdSe/CdS/ZnS QDs for the experiments presented here. Details regarding the synthesis19−21 and characterization are presented in the Methods. The steady-state absorption and photoluminescence (PL) spectra and a representative transmission electron microscopy image are shown in Figure 1a). The epitaxial shells increase the absorption cross-section of the QDs at the excitation wavelength, boost the electrochemical stability of the QDs,17 and lead to a PL quantum yield of 81% in solution (see Methods).
Figure 1.
Benchmarking the neutral CdSe/CdS/ZnS QDs in solution. (a) Steady-state absorption and PL spectra of the CdSe/CdS/ZnS QDs used throughout this work. The insets show a TEM micrograph of the QDs, which have a diameter of 10.9 ± 1.0 nm, and a schematic of the QDs. (b) 2D TA image for a pump wavelength of 400 nm and excitation density of ⟨NX⟩ = 7.9. The black dotted line shows the steady-state absorption spectrum. (c) Time-dependent excited-state absorption spectrum (or gain-map), obtained from b, where all the positive absorption is colored black, and the negative absorption (gain) is colored following the scale bar. (d) Spectral slices at a pump–probe delay time of 5 ps for increasing pump-fluence. The left image displays the differential absorption spectra, whereas the right image shows the excited-state absorption spectra. (e) Quantification of the optical gain threshold in solution, showing −ΔA (@ 5 ps pump–probe delay time) versus ⟨NX⟩ The red line indicates a heuristic fit (increasing exponential function) to the data, used to determine the gain threshold. (f) Schematic of the mechanism for low threshold optical gain in undoped and doped QDs. Upon above-bandgap excitation, both the electron and hole will cool down to the band edges. In the n-doped QDs, the 1S absorption transition is already blocked. Hence, stimulated emission does not have to compensate for the absorption process, which leads to zero-threshold optical gain.
To benchmark these QDs we first measure the optical gain threshold in solution. We determine the absorption cross section (σ = 3.6 ± 0.2 × 10–14 cm2 at the 400 nm pump wavelength) of the QDs, from the fluence dependence of Auger recombination6,22 (see the Supporting Information). Using the measured photon fluence J, we determine the average number of photogenerated excitons per QD, ⟨NX⟩ = Jσ. Figure 1b shows a color map of a TA measurement on the QDs. By adding the steady-state absorption, A0, to the transient absorption, we obtain a gain map, as shown in Figure 1c, showing in color the region of the spectrum characterized by negative absorption in the excited state, i.e., optical gain. To quantify the gain spectra and gain threshold, we take spectral slices at 5 ps, after thermalization of hot carriers, which is shown in Figure 1d. The gain of the lowest the energy transition ((1S(e) – 1S3/2(h), the 1S transition) starts red-shifted compared to the steady-state absorption spectrum but shows a distinct blueshift with increasing excitation fluence (to a maximum of 20 meV). This is in agreement with models by Bisschop et al.,23 who showed that the biexciton binding energy becomes repulsive when thick CdS shells are grown around the QDs.
The electronic transitions leading to optical gain in intrinsic and doped QDs are schematically depicted in Figure 1f. After photoexcitation above the band gap of the CdSe core, hot carriers rapidly cool to the conduction and valence band edges of the QD. Once thermalized, a second photon with an energy equal to the band gap energy can either lead to absorption or stimulated emission. Depending on the excitation density, the QDs either remain absorptive, become transparent, or show optical gain.
To quantitatively evaluate the optical gain, we spectrally average the TA spectrum over the band-edge transition at 5 ps time delay (dashed vertical lines in Figure 1d). Comparing the averaged bleach, presented in Figure 1e, with the average absorption over the same wavelength range (horizontal dashed line), we determined the 1S gain-threshold ⟨Ngain,1S⟩ to be 1.55 ± 0.07 excitons per QD. This is in quantitative agreement with the theoretical value of ⟨Ngain,1S⟩ of 1.54 for a 2-fold 1S(e) and 4-fold 1S3/2(h) degeneracy, determined considering a Poissonian distribution of excitons over the QD (section 1.1 in the Supporting Information).24 Furthermore, we observe that the absorption of the 1S transition is completely inverted at 5 ps for the highest pump fluence (⟨NX⟩ = 9.1). At high pump fluences (⟨NX⟩ ≥ 3.5), the second transition (1S(e) – 2S3/2(h), the 2S transition) shows optical gain. These results show that the neutral QDs behave nearly ideally and their gain properties are understood quantitatively.
Electrochemical Doping of QD Films
To quantify the relationship between optical gain and electronic doping, we need precise control over the doping density inside the QD film. Using spectroelectrochemical (SEC) measurements, we controllably inject carriers into the QD films, monitoring changes in the photoluminescence and absorption of the film to determine the doping density. We prepared QD films by spin-coating a QD dispersion in toluene on a conductive ITO-on-glass substrate, followed by cross-linking the QDs with 1,7-diaminoheptane, to ensure the films have a good electron mobility (see Methods).
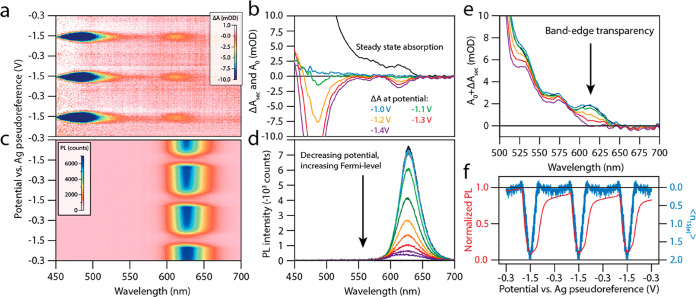
Figure 2a shows SEC differential absorption (ΔASEC) measurements. We sweep the potential between the open circuit potential (−0.30 V vs. the Ag pseudoreference electrode (PRE), i.e. −0.77 V vs. Fc/Fc+, see the Supporting Information) and −1.50 V (i.e., −1.97 V vs. Fc/Fc+), while measuring the change in absorption of the QD film. Upon electron injection into the conduction band of the QD film, we observe a decrease of several absorption transitions as a result of state filling of the 1S(e) conduction band level. Figure 2a shows three electrochemical cycles, highlighting the excellent reversibility of ΔASEC. ΔASEC-spectra at selected potentials are shown in Figure 2b. The magnitude of the band-edge bleach is equal to the ground state absorption (A0) at roughly −1.4 V, indicating that the 1S(e) level is completely filled. Figure 2c shows the corresponding SEC photoluminescence spectra as a function of applied potential. The PL intensity drops severely upon electron injection into the conduction band, an expected consequence of increased Auger decay in the n-doped QDs.17Figure 2d shows PL spectra at different potentials.
Figure 2.
Spectroelectrochemistry on a film of CdSe/CdS/ZnS QDs. The potential during all SEC measurements was swept three times between the open circuit potential and −1.5 V to check for sample stability. (a) SEC absorption measurements. Injection of electrons into the conduction band of the QDs is observed by bleaching of the band-edge (around 615 nm) and CdS shell (<550 nm) transitions. (b) ΔASEC spectra at different potentials. Charge injection starts around −1.1 V. Note that the band-edge bleach amplitude at the most negative potentials equals the amplitude of the absorption spectrum. (c) SEC PL measurements. As electrons are injected into the conduction band of the QDs, the PL quenches due to Auger recombination. (d) PL spectra at different potentials. The PL amplitude decreases because of enhanced Auger recombination. (e) Total absorption of the QD film, i.e., ΔASEC+A0. The band-edge transition becomes transparent at −1.4 V. (f) Normalized PL and amplitude of the band-edge bleach as a function of applied potential. The drop in PL coincides with the injection of charges into the conduction band of the QDs, indicating a relatively trap-free QD film. The number of electrochemically injected 1S(e) electrons oscillates between zero and two.
Figure 2e shows the absorption spectra of the charged QD films, i.e., the sum of the ΔASEC spectra and the ground-state absorption spectrum. The 1S transition becomes transparent at −1.4 V.
To quantify the charge density, we fitted a Gaussian to the 1S absorption bleach feature at every potential, as well as to the 1S feature in the ground-state absorption spectrum. The average number of electrochemically injected electrons in the 1S(e) level is given by ⟨n1S(e)⟩ = 2ΔA1S(e)/A0,1S(e), where we use the Gaussian amplitudes of the fitted 1S absorption and absorption bleach.13 The resulting values of ⟨n1S(e)⟩ at each potential are shown, together with the normalized PL intensity, in Figure 2f. Charging and discharging of the QD film is fully reversible, as the number of electrochemically injected electrons into the 1S(e) level oscillates between zero and two. Furthermore, we observe that the absorption bleach increases at the same potential as the PL starts to quench, a good indication of trap-free and electrochemically stable QDs.17,25
Ultrafast Spectroelectrochemistry
To characterize the gain response of n-doped QD films, we performed fs transient absorption (fsTA) measurements while electrochemically controlling the doping density, which we refer to as ultrafast spectroelectrochemistry. The differential absorption signal, ΔATA, can be added to the steady-state absorption spectrum of the sample to obtain the excited state absorption. The gain threshold is defined as the first excitation fluence resulting in a negative excited-state absorption.
Figure 3 presents excited-state absorption spectra for 400 nm excitation as a function of pump–probe delay time for various electrochemical doping densities ranging from ⟨n1S(e)⟩ = 0 to 2 and excitation fluences ranging from ⟨NX⟩ = 0–6.6. As optical excitation of a thin film of semiconductor material results in changes in both the absorption and reflection of the film, all TA spectra are corrected for changes in reflectivity of the sample after photoexcitation.26 The procedure for correcting the as-measured “transient-extinction” signal of the QD film is outlined in the Supporting Information.
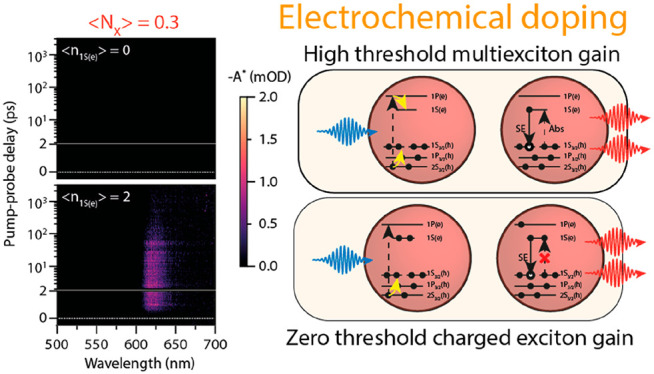
Figure 3.
Reduced threshold optical gain upon doping the QD solid with two electrons per QD. Excited-state absorption maps (excitation at 400 nm) as a function wavelength and pump–probe delay time. The upper panels show absorbance of the undoped QD solid (⟨n1S(e)⟩ = 0), whereas the bottom panels show the doped QD solid (⟨n1S(e)⟩ ∼ 2). (a) Low fluence data (⟨NX⟩ = 0.3) were multiplied by 10 for clarity. The doped QD solid already shows optical gain around 620 nm at the lowest excitation fluence. (b) For ⟨NX⟩ = 1.3, slightly below the theoretical threshold of ⟨Ngain⟩ = 1.54 for the undoped QDs, no signature of optical gain is observed in the undoped QDs, whereas the gain amplitude is increased for the doped solid. (c) For ⟨NX⟩ = 1.9 a small amount of optical gain for the undoped QDs is observed. (d) For high photoexcitation density, resulting in ⟨NX⟩ = 5.9, both the undoped and doped QD solid show full inversion of the 1S transition, and a shorter-lived gain signal originating from the 2S transition.
The top row of Figure 3 shows gain maps for the undoped film, i.e., ⟨n1S(e)⟩ = 0 (−0.3 V vs. Ag. PRE), whereas the bottom row shows gain maps are for ⟨n1S(e)⟩ = 2 (at −1.5 V vs. Ag PRE). From left to right, the excitation density increases. Figure 3a shows the excited state absorption map for ⟨NX⟩ = 0.3. For clarity, the signal amplitude is multiplied by 10. For the undoped QD film, we do not observe any optical gain over the measured spectral window. Upon increasing the excitation fluence to ⟨NX⟩ = 1.9, we start to observe gain from the 1S transition in Figure 3c. At the highest fluence presented here, ⟨NX⟩ = 5.9, we also observe optical gain from the 2S transition. In stark contrast, at a doping density of ⟨n1S(e)⟩ = 2, we observe light amplification of the 1S transition even for the lowest excitation fluence, as shown in the bottom panel of Figure 3a. Upon increasing the fluence, the optical gain amplitude increases, and we again observe optical gain from the 2S transition at ⟨NX⟩ = 5.9. The data qualitatively show that electrochemical doping can drastically reduce the optical gain threshold. In the remainder of the manuscript, we will quantify the relationship between optical gain, density of electrochemically injected carriers, and density of excitons.
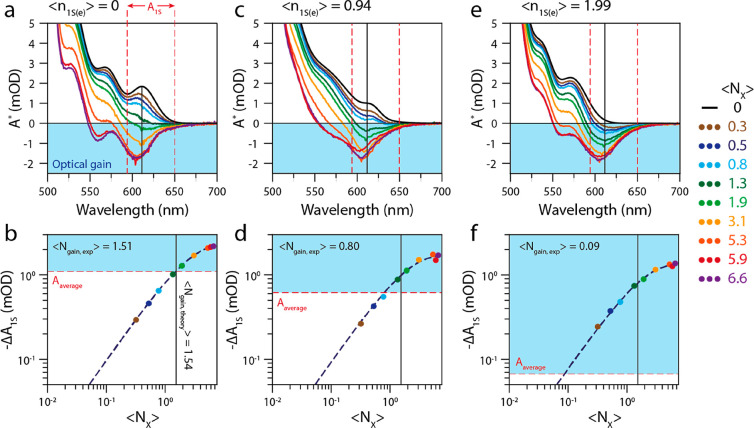
For every doping density, we determine the average number of excitons required to reach transparency of the averaged 1S transition, ⟨Ngain,1S⟩. The data for the undoped film, and the film doped with ⟨n1S(e)⟩ = 0.94 and ⟨n1S(e)⟩= 1.99 are presented in Figure 4. The upper panels of the figure show the excited-state absorption (i.e., A0 + ΔASEC + ΔATA) at a pump–probe delay time of 5 ps. The bottom panels show the gain-threshold determination (similar to Figure 1e).
Figure 4.
Gain threshold determination for different doping densities. Spectra were recorded at an excitation wavelength of 400 nm and a pump–probe delay time of 5 ps. (a) Excited-state absorption spectra at open circuit potential, where ⟨n1S(e)⟩ = 0, and for varying excitation densities. At ⟨NX⟩ = 1.9, we start to see negative absorption. For the two highest excitation densities, we also observed optical gain originating from the 2S transition. The dashed red lines show the region in between which the absorption (and bleach) amplitude is averaged. (b) Bleach amplitude (−ΔA1S) versus the excitation density ⟨NX⟩ for the 1S transition in the uncharged QD solid. The dashed red line shows the average absorption of the 1S transition above which the QD film shows optical gain. The fitted gain threshold of ⟨Ngain,1S⟩ = 1.51 agrees well with the theoretically expected gain threshold of 1.54 excitons per QD. (c) Excited-state absorption spectra at a doping density of ⟨n1S(e)⟩ = 0.94. (d) Determination of the gain threshold for ⟨n1S(e)⟩ = 0.94. The steady-state absorption at the band-edge transition is reduced, resulting in ⟨Ngain, 1S⟩ = 0.80. (e) Excited-state absorption spectra at a doping density of ⟨n1S(e)⟩ = 1.99. (f) Determination of the gain threshold for ⟨n1S(e)⟩ = 1.99. The band-edge absorption transition is transparent because of the electrochemically injected electrons, reducing ⟨Ngain,1S⟩ to 0.09 excitons per QD.
The gain properties of the undoped film (Figure 4a, b) are nearly identical to those of the QDs in solution, shown in Figure 1. We determine a spectrally averaged gain threshold of ⟨Ngain,1S⟩ = 1.51. The the QD film with a doping density ⟨n1S(e)⟩ ∼ 1 shows a reduced threshold of ⟨Ngain,1S⟩ = 0.80 (Figure 4 c, d). At the highest doping density, ⟨n1S(e)⟩ ∼ 2 (Figures 4e, f) the optical gain threshold for the integrated 1S transition is reduced to ⟨Ngain,1S⟩ = 0.09 ± 0.09 excitons/QD. For all doping densities, increasing the fluence leads to saturation of the optical gain, reaching similar maximum values for different doping densities.
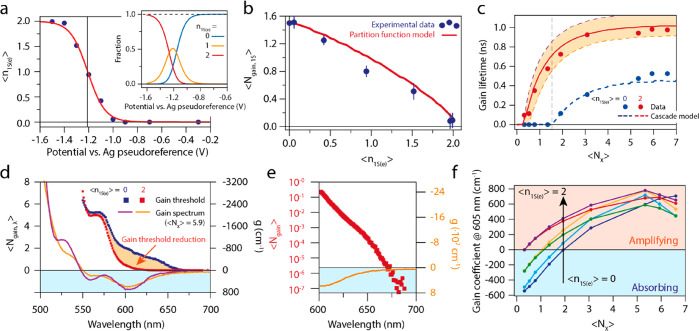
Finally, we combine all experiments shown above to develop a model that quantitatively describes optical gain in doped QDs. We model the excited-state absorption in a QD film using the transition model counting model discussed in section 1.1–1.5 in the Supporting Information, and in ref (6). As inputs, we need to know the distribution of electrons and excitons over the QDs at each potential. First, fitting a Fermi–Dirac distribution for a 2-fold degenerate level to ⟨n1S(e)⟩ as a function of the applied potential, shown in Figure 5a, we obtain the fraction of neutral, singly charged, and doubly charged QDs at each potential (see section 1.3 in the Supporting Information). Combined with a Poisson distribution of ⟨NX⟩ at each fluence this allows us to predict the gain threshold ⟨Ngain,1S⟩ as a function of ⟨n1S(e)⟩. The modeled excited-state absorption is
| 1 |
with P(⟨NX ⟩,N) a Poisson distribution for the exciton density and f(⟨n1S(e)⟩) a Fermi–Dirac function describing electrochemical state-filling of the 1S(e) level (seesection S1 in the Supporting Information). Equation 1 is numerically solved to determine the value ⟨NX⟩ where A*ensemble = 0. The prediction from this model is shown as the red solid line in Figure 5b.
Figure 5.
Quantification and modeling of measured optical gain and determination of device-relevant parameters. (a) ⟨n1S(e)⟩ versus the applied electrochemical potential. Blue data points represent the experimentally determined charge density, the red solid line is a Fermi–Dirac fit. The inset shows the distribution of neutral, singly charged, and doubly charged QDs vs applied potential as extracted from the fit. (b) Gain threshold ⟨gain,1S⟩ versus the average number of electrochemically injected electrons per QD ⟨n1S(e)⟩. The blue data points represent the experimentally determined threshold and the solid red line is a model based on Poisson statistics for photon excitation, Fermi–Dirac statistics for electron filling, and transition counting to estimate the absorption cross section of the band-edge transition. (c) Gain lifetimes as a function of ⟨NX⟩ for the neutral and doubly charged QD film. The blue and red dots are experimental data points, and the lines represent a model based on coupled rate-equations (with ⟨n1S(e)⟩ = 1.95, 1.9, and 1.85 going from top to bottom). (d) Single wavelength gain threshold ⟨Ngain,λ⟩ vs. wavelength for the neutral and ⟨n1S(e)⟩ = 2 doped QD films, shown as the blue and red squares, respectively. For comparison, we also show the excited-state absorption spectrum for the neutral and charged film for ⟨NX⟩ = 5.9 (blue and red solid lines, respectively), to demonstrate that the optical gain threshold vanishes at wavelengths where there is an appreciable gain coefficient. (e) Zoom-in of d, the spectral region from 600 to 700 nm, plotted on a logarithmic scale. We observe ⟨Ngain,λ⟩ = 1 × 10–3 to 1 × 10–5 in regions with significant negative absorption. (f) Gain coefficient at 605 nm for various doping densities. The gain coefficients saturate around 800 cm–1.
The data points in Figure 5b show the measured gain threshold ⟨Ngain,1S⟩ as a function of ⟨n1S(e)⟩, showing a decrease in threshold with increasing ⟨n1S(e)⟩. Note that the red solid line is not a fit to the data, but a predication based on independent experimental observables (i.e., the absorption cross section from fluence dependent Auger recombination data (Figure S12), and the Fermi–Dirac distribution from SEC absorption measurements, Figure 5a). The match between the experimental gain thresholds and the model prediction is excellent, demonstrating that we have quantitative control over the gain threshold, both experimentally and theoretically.
In Figure 5c, we present the lifetime of the optical gain signal for the neutral QD film (⟨n1S(e)⟩ = 0, blue data points), and the QD film with on average two electrons per QD (red data points). We define the optical gain lifetime as the amount of time after photoexcitation that the average excited state 1S absorption remains negative. The extracted gain lifetimes increase with both increasing ⟨NX⟩ and with increasing ⟨n1S(e)⟩. For undoped QD films, the highest gain lifetime is ∼0.5 ns, whereas for doped QD, it reaches ∼1 ns. To model the gain dynamics, we set up a system of coupled differential equations that take Auger decay of (charged) multiexcitons into account (see section S1.5 in the Supporting Information). From the fluence-dependent fsTA data, we extract a biexciton lifetime of 310 ps (see the Supporting Information). We assume that Auger rates scale with the number of electrons and holes as outlined by the group of Klimov,5,27,28 which allows us to model the cascade of Auger processes controlling excitonic decay. As shown in Figure 5c, we get good quantitative agreement with the experimental data.
These results demonstrate the possibility to use our analytical model to accurately describe the relationship between the carrier population and optical gain in QD solids. Furthermore, complementing the transition counting model with a description of excitonic decay allows a precise prediction of the gain lifetime. Having been validated on this data set, the model provides useful insight on the lasing characteristics of different QD materials of known band-edge degeneracies and Auger lifetimes and can be used to direct the development of laser devices based on QDs with different band-edge degeneracies and different decay rates.
So far, we have focused on the spectrally averaged
gain threshold
⟨Ngain,1S⟩, as this is most
insightful to study the effects of state filling on absorption and
stimulated emission, without complications from spectral shifts that
result from doping or optical excitation. However, for practical applications,
a more relevant value is the gain threshold at a single wavelength
where light amplification is to take place, ⟨Ngain,λ⟩. In Figure 5d, we plot ⟨Ngain,λ⟩ as a function of wavelength
for the undoped (blue squares) and the ⟨n1S(e)⟩ = 2 charged (red squares) QD film. The decrease
in the optical gain threshold is clearly visible for the 1S transition,
highlighted with the yellow area in the graph. For comparison, the
gain coefficient spectra (at a fluence of ⟨NX⟩ = 5.9) are also plotted in the same figure.
These are obtained from the excited state absorption spectra and the
film thickness d = 116 ± 13 nm (see Methods), as 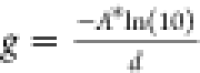 .
.
Figure 5e shows a zoom of Figure 5d, but on a logarithmic scale. We observe that the threshold practically vanished for the doped film over a significant wavelength range. It becomes clear that, defined at a single wavelength, the gain threshold is somewhat arbitrary. In addition to a low threshold, it is important that there is a significant gain coefficient at the amplified wavelength, at least large enough to compensate for losses that occur for the optical mode that is amplified. A typical loss coefficient in InGaAs/GaAs/AlGaAs laser diode arrays >50 cm–1.29 Taking this gain coefficient as the threshold for amplification we observe a record-low single-wavelength thresholds of 2.5 × 10–5 excitons per QD, corresponding to a 400 nm pump fluence of 0.4 nJ/(pulse cm2).
Figure 5f shows the gain coefficient at 605 nm as a function of ⟨NX⟩ and for various doping densities. At a fixed value of ⟨NX⟩, the gain coefficient is always significantly higher for doped QD films than for the neutral film. The maximum gain coefficient for the doped QD film is ∼800 cm–1, which is similar to the intrinsic gain coefficient of colloidal QDs in solution and III–V epitaxial semiconductors (1 × 103 cm–1).23,30 This demonstrates the great promise of electrochemically doped QD films for use as low-threshold gain media with strong light amplification. The next step, currently underway in our lab, is to employ electrochemically doped QD films in devices such as DFB gratings,16,31−34 microdisk lasers,35 and ring resonators.36
Conclusions
We have demonstrated precise experimental and theoretical control over the optical gain threshold in QD solids, via controlled and reversible electrochemical doping. After electrochemically injecting on average two electrons per QD into the 1S(e) electron level, we showed that the spectrally integrated 1S gain threshold is as low as 0.09 excitons per QD. We achieved record low single wavelength gain thresholds down to ∼1 × 10–5 excitons per QD, gain coefficients up to 800 cm–1, and a gain lifetime of ∼1 ns. Furthermore, we were able to model the gain threshold reduction for the electrochemical charging and the resulting gain lifetimes quantitatively. These results demonstrate electrochemical doping as a method to achieve optically pumped QD lasers operating at low excitation fluences.37
Methods
Synthesis of CdSe Core Nanocrystals (NCs)
The CdSe core nanocrystals were synthesized according to a method by Chen et al.20 To a 50 mL three-necked flask were added 60 mg of CdO, 280 mg of octadecylphosphonic acid (ODPA), 3 g of trioctylphosphineoxide (TOPO), and a magnetic stirring bean. This mixture of powders was heated under a vacuum to 150 °C, where the mixture melts. The mixture was slowly stirred (it prevents the CdO from creeping up the inside of the flask) and degassed at this temperature for 1 h. The mixture was heated up to 320 °C, where the liquid turned into a clear and colorless solution. Note that depending on the batch of QDs, the time it took for the solution to become clear varied from 20 min to 4 h; this has likely something to do with the impurities in one of the chemicals. One milliliter of trioctylphosphine (TOP) was added to the solution, and the temperature was raised to 380 °C, at which point 0.5 mL of a Se-precursor solution (60 mg of Se in 0.5 mL of TOP) was swiftly injected. After a specific growth time, the reaction mixture was cooled with an airgun to room temperature. For the CdSe cores in this work, we used a growth time of ±25 s. The crude product was washed once by addition of a 1:1 volume ratio of methyl acetate, followed by centrifugation at 3000 rpm and redispersion into hexane. The solution was then filtered through several Millipore filters (the polymerized ligands clog the filters easily) with a pore diameter of 0.2 μm. The filtered solution was washed and centrifuged again as described above and redispersed in hexane, and the resulting sample was stored in a nitrogen-purged glovebox for further use.
Synthesis of Cd-Oleate and Zn-Oleate for CdS and ZnS Shell Growth
For the Cd-oleate synthesis, 1.32 g of Cd-(acetate)2 was dissolved in 52.4 g of ODE and 7.4 g of OA. The mixture was heated up under a vacuum to 120 °C and left there for 3 h. Afterward, the reaction was cooled to room temperature and the Cd-oleate solution was stored in a nitrogen-purged glovebox for further use.
The Zn-oleate was made in a similar fashion. Zn(II)-(acetate)2 was mixed with 1 g of OA, 1.6 mL of ODE, and 1.6 mL of OLAM. The oleylamine serves as a stabilizing ligand for the Zn-oleate, because this has the tendency to solidify out of solution at room temperature otherwise. The mixture was heated up in a 20 mL vial inside a nitrogen-purged glovebox to 130 °C and stored there for further use. Note that the Zn-oleate solution is extremely viscous and should be handled with care when placed into a syringe.
Shell Growth of CdS and ZnS
The shell growth of CdSe QDs into core–shell–shell CdSe/CdS/ZnS nanocrystals was done according to an method adapted from Chen et al.,20 Boldt et al.,21 and Hanafi et al.19
For the CdS shell growth, 50 nmol of CdSe cores, 3.0 mL of octadecene (ODE), and NO oleylamine (OLAM, after recent work by Hanafi et al.19) were added to a 100 mL three-necked flask and degassed for 1 h at room-temperature (21 °C) and for 2 h at 120 °C to completely remove hexane, oxygen, and water. After that, the reaction solution was heated up to 310 °C under a nitrogen flow and magnetic stirring. During the heating, when the temperature reached 240 °C, a desired amount of Cd-oleate (diluted in ODE) and 1-octanethiol (diluted in 8 mL ODE) were injected dropwise into the growth solution at a rate of half a CdS monolayer per hour using a syringe pump. We define one CdS monolayer as one full layer of Cd and one full layer of S on the NC surface (i.e., half a unit cell). After the addition of the CdS shell precursors was finished, but before the growth of the ZnS shell, the core–shell QDs containing solution was degassed at a pressure of 0.5 mbar for 1 h at 120 °C.
For the ZnS shell-growth, the sulfur precursor consisted again out of 1-octanethiol diluted in ODE. The solution with freshly grown CdSe/CdS QDs was heated up to 280 °C under nitrogen flow. When the solution reached 210 °C, a desired amount of Zn-oleate and 1-octanethiol in 4 mL of ODE (in two separate syringes) was injected at a rate of 2 mL/h (roughly one monolayers of ZnS per hour). After addition of the precursors, the solution was cooled to room temperature by removing the heat with an airgun.
The solution was washed twice by addition of methanol:butanol (1:2), centrifuged at 3000 rpm for 10 min, and washed once with methyl acetate followed by centrifugation at 3000 rpm. The precipitate was each time redispersed in hexane. Finally, the solution was filtered through Millipore filters with a pore diameter of 0.2 μm and stored in a nitrogen-purged glovebox for further use.
Using the above methods, we synthesized several batches of core–shell–shell CdSe/8CdS/2ZnS QDs.
QDs-on-ITO Film Preparation
We prepared a concentrated solution (roughly 20 mg/mL) of QDs in toluene. Before spin-coating, the ITO slide is cleaned by sonication in isopropanol and rinsed with ethanol and acetone, followed by drying with an airgun. The slide is placed inside a UV-ozone cleaner for 30 min prior to spin-coating to increase the wetting of the QD solution on the ITO. The spin-coating was performed by gently dropcasting 40 μL of the QD dispersion on the ITO slide, followed by spin-coating for 1 min at 1000 rpm (with a ramp rate of 200 rpm/s). The film is taken inside a nitrogen-purged glovebox, where we dropcast a solution of 0.5 M 1,7-diaminoheptane in methanol on top of the ITO slide, letting the methanol of this solution evaporate, followed by submerging the substrate into clean methanol. This ligand exchange/stripping procedure is repeated two more times, to ensure proper ligand exchange/stripping. Without performing this treatment, we are not able to electrochemically inject any electrons into the 1S(e) conduction band state of the QD film, as the film is not conductive enough and the electrons cannot hop from QD to QD.
Steady-State Absorption and Photoluminescence Measurements
Absorption spectra were measured on a double-beam PerkinElmer Lambda 1050 UV/vis spectrometer; in case of the QD films on ITO, the sample was measured inside an integrating sphere and an empty ITO was measured separately for background correction. Photoluminescence spectra were recorded on an Edinburgh Instruments FLS980 spectrofluorimeter equipped with double grating monochromators for both excitation and emission paths and a 450 W xenon lamp as an excitation source.
Transmission Electron Microscopy (TEM)
TEM images were acquired using a JEOL JEM-1400 plus TEM microscope operating at 120 kV. Samples for TEM imaging were prepared by dropcasting a dilute solution of QDs onto a Formvar and carbon-coated copper (400-mesh) TEM grid.
fs-Transient Absorption (TA) Spectroscopy
fs-TA measurements are performed on solutions of the CdSe(/CdS/ZnS) QDs in hexane or toluene loaded inside an airtight cuvette inside a nitrogen-purged glovebox. A Yb-KGW oscillator (Light Conversion, Pharos SP) is used to produce 180 fs photon pulses with a wavelength of 1028 nm and at a frequency of 5 kHz. The pump beam is obtained by sending the fundamental beam through an optical parametric amplifier (OPA) equipped with a second harmonic module (Light Conversion, Orpheus), performing nonlinear frequency mixing and producing an output beam whose wavelength can be tuned in the 310–1330 nm window. A small fraction of the fundamental beam power is used to produce a broadband probe spectrum (480–1600 nm), by supercontinuum generation in a sapphire crystal. The pump beam is transmitted through a mechanical chopper operating at 2.5 kHz, allowing one in every two pump pulses to be transmitted. Pump and probe beam overlap at the sample position with a small angle (roughly 8°), and with a relative time delay controlled by an automated delay stage. After transmission through the sample, the pump beam is dumped while the probe is collected at a detector (Ultrafast Systems, Helios). During the experiments, we make sure the pump and probe beam have orthogonal polarizations (i.e., one of them is vertically polarized, the other horizontally), to reduce the influence of pump scattering into our detector. The differential absorbance is obtained via ΔA = 10log(Ion/ Ioff), where I is the probe light incident on the detector with either pump on or pump off. TA data are corrected for probe-chirp via a polynomial correction to the coherent artifact. Pump photon fluence was estimated by measuring the pump beam transmission through a 1 mm-radius pinhole with a thermopile sensor (Coherent, PS19Q).
We also measure transient reflection (TR) spectra to obtain the true change in absorption in transient transmission experiments. The correction method is outlined in the Supporting Information.
Photoluminescence Quantum Yield (PLQY) Measurements
We measured the PLQY of the NC dispersions with respect to a rhodamine 101 solution in ethanol. The PLQY was calculated using the following equation:
Where PLQYrhodamine 101 is set to be 95%, IPL is the intensity of the photoluminescence signal of either the QD solution or the rhodamine 101 solution, nhexane/ethanol is the refractive index of hexane or ethanol at 530 nm (1.377 and 1.3630), and fx is the fraction of absorbed light of species x, calculated as fx = 1–10–ODx), where ODx is the optical density of the solution containing either the QDs or the rhodamine 101. We determined the PLQY of the CdSe/8CdS/2ZnS core–shell–shell QDs to be 81%.
Spectroelectrochemical (SEC) Measurements
The SEC measurements were all performed in a nitrogen-purged glovebox. As an electrolyte, we used an 0.1 M LiClO4 solution in acetonitrile, which was dried with an Innovative Technology PureSolv Micro column. The QD film was immersed in the electrolyte solution, together with a Ag wire pseudoreference electrode and a Pt sheet counter electrode. The potential of the NC film on ITO was controlled with a PGSTAT128N Autolab potentiostat. Changes in the absorption or PL of the NC film as a function of applied potential were recorded simultaneously with a cyclic voltammogram with a fiber-based UV–vis spectrometer (USB2000, Ocean Optics). For the film, the measurements were started at the open-circuit potential (VOC = −0.3 V w.r.t. Ag wire, i.e., −0.77 V vs. Fc/Fc+, see the Supporting Information)) while scanning with a rate of 20 mV/s. Unless stated otherwise, all potentials are given w.r.t. the Ag pseudoreference. For SEC measurements combined with fsTA, we loaded the samples inside a nitrogen purged glovebox into a leak-tight sample holder (see the Supporting Information for more information).
Acknowledgments
A.J.H., J.J.G., S.G., and W.v.d.S. gratefully acknowledge financial support from the European Research Council Horizon 2020 ERC Grant Agreement 678004 (Doping on Demand). G.G. acknowledges financial support from NWO-TTW (Project 13903, Stable and Non-Toxic Nanocrystal Solar Cells). We gratefully acknowledge fruitful discussions with Dr. Freddy Rabouw, Stijn Hinterding, and Sander Vonk (Utrecht University) on modelling the electrochemical electron injection into QDs.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.0c07365.
Data analysis: all acquired data, derivation of and the correction for changes in reflection upon photoexcitation, simulating the gain threshold and gain lifetime using a Fermi–Dirac type model; the data that support the findings of this study and the codes used to analyze them (Python) are also available from the corresponding authors upon reasonable request. (PDF)
Author Present Address
† G.G. is currently at Center for Nanophotonics, AMOLF, Science Park 104, Amsterdam 1098 XG, The Netherlands.
Author Present Address
‡ W.v.d.S. is currently at Inorganic Chemistry and Catalysis, Debye Institute for Nanomaterials Science, Utrecht University, Universiteitsweg 99, Utrecht 3584 CG, The Netherlands.
The authors declare no competing financial interest.
Supplementary Material
References
- Kovalenko M. V.; Manna L.; Cabot A.; Hens Z.; Talapin D. V.; Kagan C. R.; Klimov V. I.; Rogach A. L.; Reiss P.; Milliron D. J.; et al. Prospects of Nanoscience with Nanocrystals. ACS Nano 2015, 9, 1012–1057. 10.1021/nn506223h. [DOI] [PubMed] [Google Scholar]
- Geiregat P.; Van Thourhout D.; Hens Z. A Bright Future for Colloidal Quantum Dot Lasers. NPG Asia Mater. 2019, 11, 41. 10.1038/s41427-019-0141-y. [DOI] [Google Scholar]
- Klimov V. I.; Mikhailovsky A. A.; Xu S.; Malko A.; Hollingsworth J. A.; Leatherdale C. A.; Eisler H. J.; Bawendi M. G. Optical Gain and Stimulated Emission in Nanocrystal Quantum Dots. Science (Washington, DC, U. S.) 2000, 290, 314–317. 10.1126/science.290.5490.314. [DOI] [PubMed] [Google Scholar]
- Kagan C. R.; Lifshitz E.; Sargent E. H.; Talapin D. V. Building Devices from Colloidal Quantum Dots. Science 2016, 353, 545–610. 10.1126/science.aac5523. [DOI] [PubMed] [Google Scholar]
- Klimov V. I.; Mikhailovsky A. A.; McBranch D. W.; Leatherdale C. A.; Bawendi M. G. Quantization of Multiparticle Auger Rates in Semiconductor Quantum Dots. Science (Washington, DC, U. S.) 2000, 287, 1011–1013. 10.1126/science.287.5455.1011. [DOI] [PubMed] [Google Scholar]
- Grimaldi G.; Geuchies J. J.; van der Stam W.; du Fossé I.; Brynjarsson B.; Kirkwood N.; Kinge S.; Siebbeles L. D. A.; Houtepen A. J. Spectroscopic Evidence for the Contribution of Holes to the Bleach of Cd-Chalcogenide Quantum Dots. Nano Lett. 2019, 19, 3002–3010. 10.1021/acs.nanolett.9b00164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu K.; Park Y.-S.; Lim J.; Klimov V. I. Towards Zero-Threshold Optical Gain Using Charged Semiconductor Quantum Dots. Nat. Nanotechnol. 2017, 12, 1140–1147. 10.1038/nnano.2017.189. [DOI] [PubMed] [Google Scholar]
- Lim J.; Park Y. S.; Wu K.; Yun H. J.; Klimov V. I. Droop-Free Colloidal Quantum Dot Light-Emitting Diodes. Nano Lett. 2018, 18, 6645–6653. 10.1021/acs.nanolett.8b03457. [DOI] [PubMed] [Google Scholar]
- Fan F.; Voznyy O.; Sabatini R. P.; Bicanic K. T.; Adachi M. M.; McBride J. R.; Reid K. R.; Park Y.-S.; Li X.; Jain A.; Quintero-Bermudez R.; Saravanapavanantham M.; Liu M.; Korkusinski M.; Hawrylak P.; Klimov V. I.; Rosenthal S. J.; Hoogland S.; Sargent E. H. Continuous-Wave Lasing in Colloidal Quantum Dot Solids Enabled by Facet-Selective Epitaxy. Nature 2017, 544, 75–79. 10.1038/nature21424. [DOI] [PubMed] [Google Scholar]
- Klimov V. I.; Ivanov S. A.; Nanda J.; Achermann M.; Bezel I.; McGuire J. A.; Piryatinski A. Single-Exciton Optical Gain in Semiconductor Nanocrystals. Nature 2007, 447, 441–446. 10.1038/nature05839. [DOI] [PubMed] [Google Scholar]
- Geiregat P.; Houtepen A. J.; Sagar L. K.; Infante I.; Zapata F.; Grigel V.; Allan G.; Delerue C.; Van Thourhout D.; Hens Z. Continuous-Wave Infrared Optical Gain and Amplified Spontaneous Emission at Ultralow Threshold by Colloidal HgTe Quantum Dots. Nat. Mater. 2018, 17, 35–42. 10.1038/nmat5000. [DOI] [PubMed] [Google Scholar]
- Shim M.; Guyot-Sionnest P. N-Type Colloidal Semiconductor Nanocrystals. Nature 2000, 407, 981–983. 10.1038/35039577. [DOI] [PubMed] [Google Scholar]
- Wang C.; Shim M.; Guyot-Sionnest P. Electrochromic Nanocrystal Quantum Dots. Science (Washington, DC, U. S.) 2001, 291, 2390–2392. 10.1126/science.291.5512.2390. [DOI] [PubMed] [Google Scholar]
- Yu D.; Wang C.; Guyot-Sionnest P. N-Type Conducting CdSe Nanocrystal Solids. Science (Washington, DC, U. S.) 2003, 300, 1277–1280. 10.1126/science.1084424. [DOI] [PubMed] [Google Scholar]
- Wang C.; Wehrenberg B. L.; Woo C. Y.; Guyot-Sionnest P. Light Emission and Amplification in Charged CdSe Quantum Dots. J. Phys. Chem. B 2004, 108, 9027–9031. 10.1021/jp0489830. [DOI] [Google Scholar]
- Kozlov O. V.; Park Y. S.; Roh J.; Fedin I.; Nakotte T.; Klimov V. I. Sub-Single-Exciton Lasing Using Charged Quantum Dots Coupled to a Distributed Feedback Cavity. Science (Washington, DC, U. S.) 2019, 365, 672–675. 10.1126/science.aax3489. [DOI] [PubMed] [Google Scholar]
- Van Der Stam W.; Grimaldi G.; Geuchies J. J.; Gudjonsdottir S.; Van Uffelen P. T.; Van Overeem M.; Brynjarsson B.; Kirkwood N.; Houtepen A. J. Electrochemical Modulation of the Photophysics of Surface-Localized Trap States in Core/Shell/(Shell) Quantum Dot Films. Chem. Mater. 2019, 31, 8484–8493. 10.1021/acs.chemmater.9b02908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanmaekelbergh D.; Houtepen A. J.; Kelly J. J. Electrochemical Gating: A Method to Tune and Monitor the (Opto)Electronic Properties of Functional Materials. Electrochim. Acta 2007, 53, 1140–1149. 10.1016/j.electacta.2007.02.045. [DOI] [Google Scholar]
- Hanifi D. A.; Bronstein N. D.; Koscher B. A.; Nett Z.; Swabeck J. K.; Takano K.; Schwartzberg A. M.; Maserati L.; Vandewal K.; van de Burgt Y.; Salleo A.; Alivisatos P. A. Redefining Near-Unity Luminescence in Quantum Dots with Photothermal Threshold Quantum Yield. Science 2019, 363, 1199–1202. 10.1126/science.aat3803. [DOI] [PubMed] [Google Scholar]
- Chen O.; Zhao J.; Chauhan V. P.; Cui J.; Wong C.; Harris D. K.; Wei H.; Han H.-S.; Fukumura D.; Jain R. K.; Bawendi M. G. Compact High-Quality CdSe-CdS Core-Shell Nanocrystals with Narrow Emission Linewidths and Suppressed Blinking. Nat. Mater. 2013, 12, 445–451. 10.1038/nmat3539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boldt K.; Kirkwood N.; Beane G. A.; Mulvaney P. Synthesis of Highly Luminescent and Photo-Stable, Graded Shell CdSe/Cd x Zn 1-x S Nanoparticles by in Situ Alloying. Chem. Mater. 2013, 25, 4731–4738. 10.1021/cm402645r. [DOI] [Google Scholar]
- Makarov N. S.; Guo S.; Isaienko O.; Liu W.; Robel I.; Klimov V. I. Spectral and Dynamical Properties of Single Excitons, Biexcitons, and Trions in Cesium-Lead-Halide Perovskite Quantum Dots. Nano Lett. 2016, 16, 2349–2362. 10.1021/acs.nanolett.5b05077. [DOI] [PubMed] [Google Scholar]
- Bisschop S.; Geiregat P.; Aubert T.; Hens Z. The Impact of Core/Shell Sizes on the Optical Gain Characteristics of CdSe/CdS Quantum Dots. ACS Nano 2018, 12, 9011–9021. 10.1021/acsnano.8b02493. [DOI] [PubMed] [Google Scholar]
- Efros A. L.; Rosen M.; Kuno M.; Nirmal M.; Norris D.; Bawendi M. Band-Edge Exciton in Quantum Dots of Semiconductors with a Degenerate Valence Band: Dark and Bright Exciton States. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 4843–4856. 10.1103/PhysRevB.54.4843. [DOI] [PubMed] [Google Scholar]
- Jha P. P.; Guyot-Sionnest P. Photoluminescence Switching of Charged Quantum Dot Films. J. Phys. Chem. C 2007, 111, 15440–15445. 10.1021/jp075042p. [DOI] [Google Scholar]
- Ghosh T.; Aharon S.; Shpatz A.; Etgar L.; Ruhman S. Reflectivity Effects on Pump-Probe Spectra of Lead Halide Perovskites: Comparing Thin Films versus Nanocrystals. ACS Nano 2018, 12, 5719–5725. 10.1021/acsnano.8b01570. [DOI] [PubMed] [Google Scholar]
- Klimov V. I.; McGuire J. A.; Schaller R. D.; Rupasov V. I. Scaling of Multiexciton Lifetimes in Semiconductor Nanocrystals. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 77, 195324. 10.1103/PhysRevB.77.195324. [DOI] [Google Scholar]
- García-Santamaría F.; Brovelli S.; Viswanatha R.; Hollingsworth J. A.; Htoon H.; Crooker S. A.; Klimov V. I. Breakdown of Volume Scaling in Auger Recombination in CdSe/CdS Heteronanocrystals: The Role of the Core-Shell Interface. Nano Lett. 2011, 11, 687–693. 10.1021/nl103801e. [DOI] [PubMed] [Google Scholar]
- Kabanov V. V.; Lebiadok Y. V.; Ramanenka A. A.; Ryabtsev A. G.; Ryabtsev G. I.; Smal A. S.; Mehta S. K. Loss Coefficient for Amplified Luminescence of Laser Diode Arrays. J. Appl. Spectrosc. 2011, 77, 810–816. 10.1007/s10812-011-9406-0. [DOI] [Google Scholar]
- Pietryga J. M.; Park Y.-S.; Lim J.; Fidler A. F.; Bae W. K.; Brovelli S.; Klimov V. I. Spectroscopic and Device Aspects of Nanocrystal Quantum Dots. Chem. Rev. 2016, 116, 10513–10622. 10.1021/acs.chemrev.6b00169. [DOI] [PubMed] [Google Scholar]
- Prins F.; Kim D. K.; Cui J.; De Leo E.; Spiegel L. L.; McPeak K. M.; Norris D. J. Direct Patterning of Colloidal Quantum-Dot Thin Films for Enhanced and Spectrally Selective Out-Coupling of Emission. Nano Lett. 2017, 17, 1319–1325. 10.1021/acs.nanolett.6b03212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y.; Guilhabert B.; Herrnsdorf J.; Zhang Y.; Mackintosh A. R.; Pethrick R. A.; Gu E.; Laurand N.; Dawson M. D. Flexible Distributed-Feedback Colloidal Quantum Dot Laser. Appl. Phys. Lett. 2011, 99, 241103. 10.1063/1.3659305. [DOI] [Google Scholar]
- Roh K.; Dang C.; Lee J.; Chen S.; Steckel J. S.; Coe-Sullivan S.; Nurmikko A. Surface-Emitting Red, Green, and Blue Colloidal Quantum Dot Distributed Feedback Lasers. Opt. Express 2014, 22, 18800. 10.1364/OE.22.018800. [DOI] [PubMed] [Google Scholar]
- Roh J.; Park Y.-S.; Lim J.; Klimov V. I. Optically Pumped Colloidal-Quantum-Dot Lasing in LED-like Devices with an Integrated Optical Cavity. Nat. Commun. 2020, 11, 271. 10.1038/s41467-019-14014-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Y.; Xie W.; Bisschop S.; Aubert T.; Brainis E.; Geiregat P.; Hens Z.; Van Thourhout D. On-Chip Single-Mode Distributed Feedback Colloidal Quantum Dot Laser under Nanosecond Pumping. ACS Photonics 2017, 4, 2446–2452. 10.1021/acsphotonics.7b00644. [DOI] [Google Scholar]
- Le Feber B.; Prins F.; De Leo E.; Rabouw F. T.; Norris D. J. Colloidal-Quantum-Dot Ring Lasers with Active Color Control. Nano Lett. 2018, 18, 1028–1034. 10.1021/acs.nanolett.7b04495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geuchies J. J.; Brynjarsson B.; Grimaldi G.; Gudjonsdottir S.; van der Stam W.; Evers W. H.; Houtepen A. J.. Quantitative Electrochemical Control over Optical Gain in Quantum-Dot Solids. Arxiv (cond-mat.mtrl-sci), June 19, 2020, Ver. 2. https://arxiv.org/abs/2006.10647 [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.