Fig 3. 1D admixture scenario.

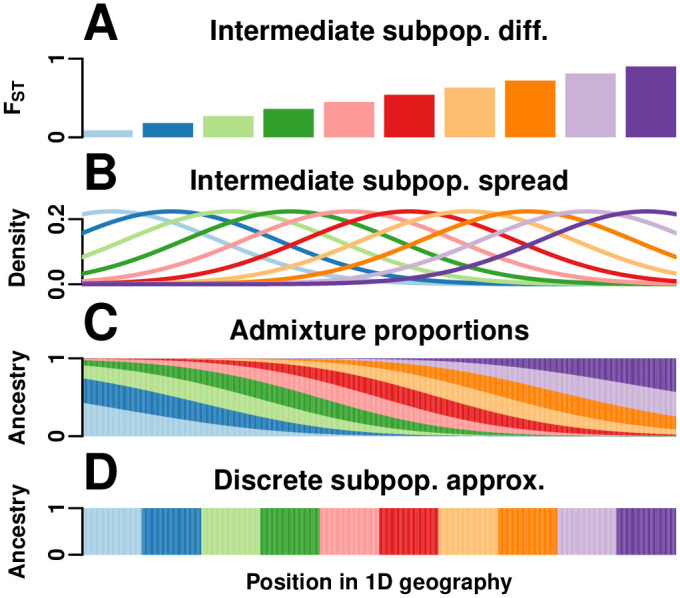
We model a 1D geography population that departs strongly from the independent subpopulations model. (A) K = 10 intermediate subpopulations, evenly spaced on a line, evolved independently in the past with F_ST increasing with distance, which models a sequence of increasing founder effects (from left to right) to mimic the global human population. (B) Once differentiated, individuals in these intermediate subpopulations spread by random walk modeled by Normal densities. (C) n = 1000 individuals, sampled evenly in the same geographical range, are admixed proportionally to the previous Normal densities. Thus, each individual draws most of its alleles from the closest intermediate subpopulation, and draws the fewest alleles from the most distant populations. Long-distance random walks of intermediate subpopulation individuals results in kinship for admixed individuals that decays smoothly with distance in Fig 2B. (D) For F_ST estimators that require a partition of individuals into subpopulations, individuals are clustered by geographical position (K = 10).