Summary
The false discovery rate (FDR) measures the proportion of false discoveries among a set of hypothesis tests called significant. This quantity is typically estimated based on p-values or test statistics. In some scenarios, there is additional information available that may be used to more accurately estimate the FDR. We develop a new framework for formulating and estimating FDRs and q-values when an additional piece of information, which we call an “informative variable”, is available. For a given test, the informative variable provides information about the prior probability a null hypothesis is true or the power of that particular test. The FDR is then treated as a function of this informative variable. We consider two applications in genomics. Our first application is a genetics of gene expression (eQTL) experiment in yeast where every genetic marker and gene expression trait pair are tested for associations. The informative variable in this case is the distance between each genetic marker and gene. Our second application is to detect differentially expressed genes in an RNA-seq study carried out in mice. The informative variable in this study is the per-gene read depth. The framework we develop is quite general, and it should be useful in a broad range of scientific applications.
Keywords: eQTL, FDR, Functional data analysis, Genetics of gene expression, Kernel density estimation, Local false discovery rate, Multiple hypothesis testing, q-value, RNA-seq, Sequencing depth
1. Introduction
Multiple testing is now routinely conducted in many scientific areas. For example, in genomics, RNA-seq technology is often utilized to test thousands of genes for differential expression among two or more biological conditions. In expression quantitative trait loci (eQTL) studies, all pairs of genetic markers and gene expression traits can be tested for associations, which often involves millions or more hypothesis tests. The false discovery rate (FDR, Benjamini and Hochberg, 1995) and the q-value (Storey, 2002, 2003) are often employed to determine significance thresholds and quantify the overall error rate when testing a large number of hypotheses simultaneously. Therefore, improving the accuracy in estimating FDRs and q-values remains an important problem.
In many emerging applications, additional information on the status of a null hypothesis or the power of a test may be available to help better estimate the FDR and q-value. For example, in eQTL studies, gene–single nucleotide polymorphism (SNP) basepair distance informs the prior probability of association between a gene–SNP pair, with local associations generally more likely than distal associations (Brem and others, 2002; Doss and others, 2005; Ronald and others, 2005). A second example comes from RNA-seq studies, for which per-gene read depth informs the statistical power to detect differential gene expression (Tarazona and others, 2011; Cai and others, 2012) or the prior probability of differential gene expression (Robinson and others, 2015). Genes with more sequencing reads mapped to them (i.e., higher per-gene read depth) have greater ability to detect differential expression or may be more likely to be differentially expressed than do low depth genes.
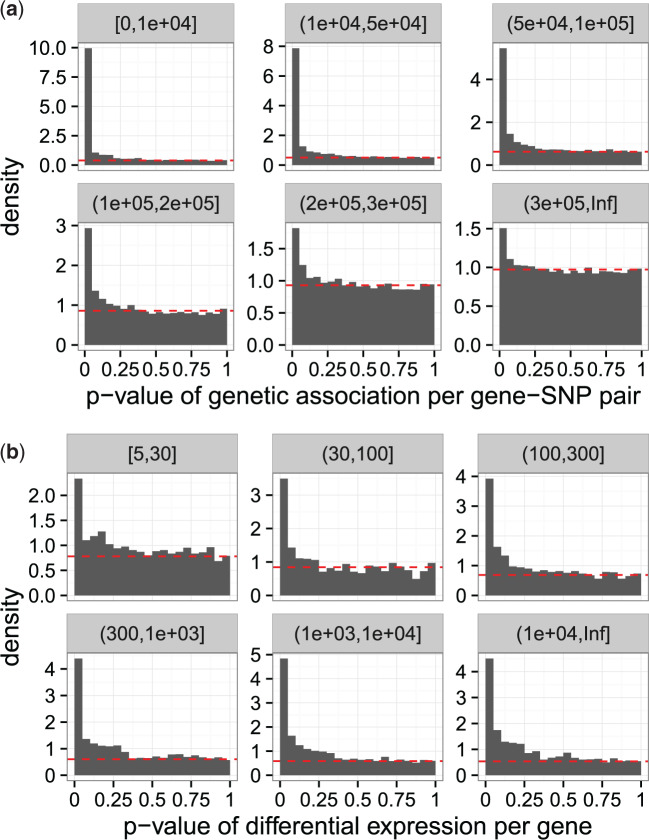
Figure 1 shows results from multiple testing on a genetics of gene expression study (Smith and Kruglyak, 2008) and an RNA-seq differential expression study (Bottomly and others, 2011). In the genetics of gene expression study, the p-values are subdivided according to six different gene–SNP basepair distance strata. In the RNA-seq study, the p-values are subdivided into six different strata of per-gene read depth. It can be seen in both cases that the proportion of true null hypotheses and the power to identify significant tests vary in a systematic manner across the strata. The goal of this article is to take advantage of this phenomenon so that we may improve the accuracy of calling tests significant and do so without having to create artificial strata as in Figure 1.
Fig. 1.
(a) P-value histograms of Wilcoxon tests for genetic association between genes and SNPs for the eQTL experiment in Smith and Kruglyak (2008), divided into six strata based on the gene–SNP basepair distance indicated by the strip names. The null hypothesis is “no association between a gene–SNP pair”. (b) P-value histograms for assessing differential gene expression in the RNA-seq study in Bottomly and others (2011), divided into six strata based on per-gene read depth indicated by the strip names. The null hypothesis is “no differential expression (for a gene) between two conditions”. In each subplot, the estimated proportion of true null hypotheses for all hypotheses in the corresponding stratum is based on Storey (2002) and indicated by the horizontal dashed line. It can be seen that gene–SNP genetic distance or per-gene read depth affects the prior probability of a gene–SNP association or differential gene expression.
We propose the functional FDR (fFDR) methodology that efficiently incorporates additional quantitative information for estimating the FDR and q-values. Specifically, we code additional information into a quantitative informative variable and extend the Bayesian framework for FDR pioneered in Storey (2003) to incorporate this informative variable. This leads to a functional proportion of true null hypotheses (or “functional null proportion” for short) and a functional power function. From this, we derive the optimal decision rule utilizing the informative variable. We then provide estimates of functional FDRs, functional local FDRs, and functional q-values to utilize in practice.
Related ideas have been developed, such as p-value weighting (Genovese and others, 2006; Roquain and van de Wiel, 2009; Hu and others, 2010; Ignatiadis and others, 2016; Ignatiadis and Huber, 2018), stratified FDR control (Sun and others, 2006), stratified local FDR thresholding (Ochoa and others, 2015), and covariate-adjusted conditional FDR estimation (Boca and Leek, 2018). Stratified FDR and local FDR rely on clearly defined strata, which may not always be available or make the best use of information. Covariate-adjusted conditional FDR estimation focuses on only one component of the FDR. P-value weighting has been a successful strategy. The methods in Genovese and others (2006) and Roquain and van de Wiel (2009) regard each hypothesis as a group and assign a weight to the p-value associated with a hypothesis, whereas those in Hu and others (2010), Ignatiadis and others (2016), and Ignatiadis and Huber (2018) partition hypotheses in groups and assign a weight to all p-values in a group. In particular, weights for the “independent hypothesis weighting (IHW)” method proposed by Ignatiadis and others (2016) and Ignatiadis and Huber (2018) are derived from non-trivial optimization algorithms. However, for a p-value weighting method, it remains challenging to derive weights that indeed result in improved power subject to a target FDR level, and how to obtain optimal weights under different optimality criteria is still an open problem. Furthermore, for a p-value weighting procedure that is also based on partitioning hypotheses into groups, its inferential results can be considerably affected by how the groups are formed.
Our methodology serves as an alternative to p-value weighting. We are motivated by similar scientific applications as the IHW method which employs a covariate to improve the power of multiple testing and is based on partitioning hypotheses into groups and p-value weighting. The authors of the IHW method have shown that this method has advantages over several existing methods including those of Benjamini and Hochberg (1995), Hu and others (2010), Scott and others (2015), and Cai and Sun (2009). However, our approach is distinct from the IHW method since the latter is a weighted version of the Benjamini–Hochberg procedure (Benjamini and Hochberg, 1995). In contrast, we work with a Bayesian model developed in Storey (2003), provide direct calculations of optimal significance thresholds, and take an empirical Bayes strategy to estimate several FDR quantities. As earlier frequentist and Bayesian approaches to the FDR in the standard scenario both proved to be important, our contribution here should serve to complement the p-value weighting strategy.
To demonstrate the effectiveness of our proposed methodology, we conduct simulations and analyze two genomics studies, an RNA-seq differential expression study and a genetics of gene expression study. In doing so, we uncover important operating characteristics of the fFDR methodology and we also provide several strategies for visualizing and interpreting results. Although our applications are focused on genomics, we anticipate the framework presented here will be useful in a wide range of scientific problems.
This rest of the article is organized as follows. We formulate the fFDR methodology in Section 2 and provide its implementation in Section 3. Two applications of the methodology are given in Section 4. We end the article with a discussion in Section 5.
2. The functional FDR framework
In this section, we formulate the fFDR theory and methodology. To this end, we first introduce our model, provide formulas for the positive false discovery rate (pFDR), positive false non-discovery rate (pFNR), and q-value, and then describe the significance rule based on the q-value.
2.1. Joint model for p-value, hypothesis status, and informative variable
Let 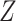 be the informative variable that is uniformly distributed on the interval
be the informative variable that is uniformly distributed on the interval 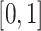 , i.e.,
, i.e., 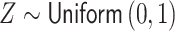 . For example,
. For example, 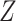 can denote the quantiles of the per-gene read depths in an RNA-seq study or the quantiles of the genomic distances in an eQTL experiment. Denote the status of the null hypothesis by
can denote the quantiles of the per-gene read depths in an RNA-seq study or the quantiles of the genomic distances in an eQTL experiment. Denote the status of the null hypothesis by 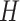 , such that
, such that 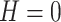 when the null hypothesis is true and
when the null hypothesis is true and 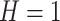 when the alternative hypothesis is true. We assume that conditional on
when the alternative hypothesis is true. We assume that conditional on 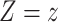 the null hypothesis is a priori true with probability
the null hypothesis is a priori true with probability 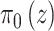 , i.e.,
, i.e.,
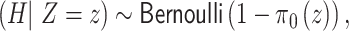 |
(2.1) |
where the function 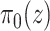 ranges in
ranges in 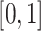 . We call
. We call 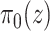 the “prior probability of the null hypothesis”, “functional proportion of true null hypotheses”, or “functional null proportion.” When
the “prior probability of the null hypothesis”, “functional proportion of true null hypotheses”, or “functional null proportion.” When 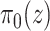 is constant, it will be simply denoted by
is constant, it will be simply denoted by 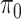 .
.
To formulate the distribution of the p-value, 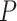 , we assume the following: (i) when the null hypothesis is true,
, we assume the following: (i) when the null hypothesis is true, 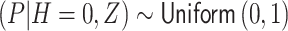 regardless of the value of
regardless of the value of 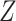 ; (ii) when the null hypothesis is false, the conditional density of
; (ii) when the null hypothesis is false, the conditional density of 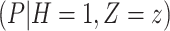 is
is 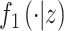 . The conditional density of
. The conditional density of 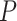 given
given 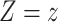 is then
is then
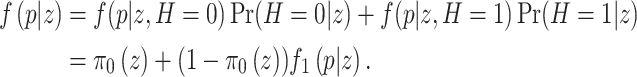 |
(2.2) |
Since 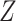 has constant density
has constant density 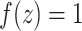 , the joint density
, the joint density 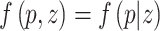 for all
for all 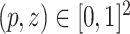 so that
so that
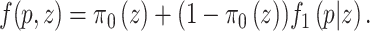 |
(2.3) |
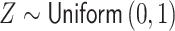 and the representation in equation (2.3) are important since they enable more straightforward estimation of
and the representation in equation (2.3) are important since they enable more straightforward estimation of 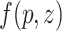 than
than 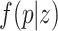 .
.
2.2. Optimal statistic
Now suppose there are  hypothesis tests, with
hypothesis tests, with 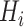 for
for 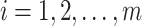 indicating the status of each hypothesis test as above. For example,
indicating the status of each hypothesis test as above. For example, 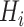 can denote whether gene
can denote whether gene 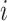 is differentially expressed or not, or whether there is an association between the
is differentially expressed or not, or whether there is an association between the 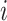 th gene–SNP pair. For the
th gene–SNP pair. For the 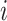 th hypothesis test, let its calculated p-value be
th hypothesis test, let its calculated p-value be 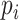 and its measured informative variable be
and its measured informative variable be 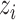 ; additionally, let
; additionally, let 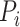 and
and 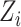 be their respective random variable representations.
be their respective random variable representations.
Let 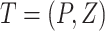 and
and 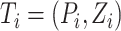 for
for 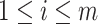 . Suppose the triples
. Suppose the triples 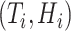 are independent and identically distributed (i.i.d.) as
are independent and identically distributed (i.i.d.) as 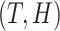 . If the same significance region
. If the same significance region 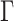 in
in 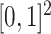 is used for the
is used for the 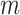 hypothesis tests, then identical arguments in the proof of Theorem 1 in Storey (2003) imply that
hypothesis tests, then identical arguments in the proof of Theorem 1 in Storey (2003) imply that 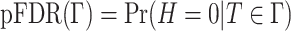 and
and 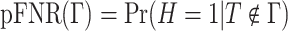 , where pFDR is the positive false discovery rate and pFNR is the false non-discovery rate as defined in Storey (2003). The bivariate function
, where pFDR is the positive false discovery rate and pFNR is the false non-discovery rate as defined in Storey (2003). The bivariate function
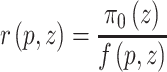 |
(2.4) |
defined on 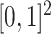 is the posterior probability that the null hypothesis is true given the observed pair
is the posterior probability that the null hypothesis is true given the observed pair 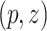 of p-value and informative variable. Note that
of p-value and informative variable. Note that 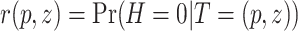 . So,
. So, 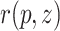 is an extension of the local FDR (Efron and others, 2001; Storey, 2003) also known as the posterior error probability (Kall and others, 2008). Straightforward calculation shows that
is an extension of the local FDR (Efron and others, 2001; Storey, 2003) also known as the posterior error probability (Kall and others, 2008). Straightforward calculation shows that
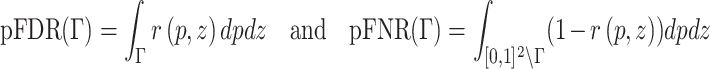 |
(2.5) |
Define significance regions 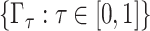 with
with
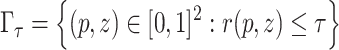 |
(2.6) |
such that test  is statistically significant if and only if
is statistically significant if and only if  . Then by identical arguments in Section 6 leading up to Corollary 4 in Storey (2003),
. Then by identical arguments in Section 6 leading up to Corollary 4 in Storey (2003), 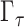 gives the Bayes rule for the Bayes error
gives the Bayes rule for the Bayes error
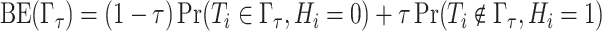 |
(2.7) |
for each 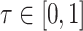 . Therefore, by arguments analogous to those in Storey (2003),
. Therefore, by arguments analogous to those in Storey (2003), 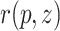 is the optimal statistic for the Bayes rule with Bayes error (2.7).
is the optimal statistic for the Bayes rule with Bayes error (2.7).
2.3. Q-value based decision rule
With the statistic 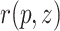 in (2.4) and nested significance regions
in (2.4) and nested significance regions 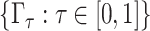 with
with 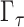 defined by (2.6), the definition of q-value in Storey (2003) implies that the q-value for the observed statistic
defined by (2.6), the definition of q-value in Storey (2003) implies that the q-value for the observed statistic 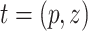 is
is
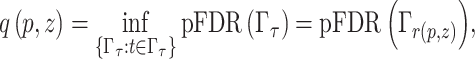 |
(2.8) |
where the second equality follows from Theorem 2 in Storey (2003), noting that 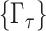 are constructed from the posterior probabilities
are constructed from the posterior probabilities 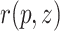 . Estimating the q-value in (2.8) will be discussed in Section 3.3.
. Estimating the q-value in (2.8) will be discussed in Section 3.3.
Let 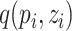 denote the q-value of
denote the q-value of 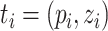 for the
for the 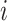 th null hypothesis
th null hypothesis 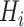 . At a target pFDR level
. At a target pFDR level 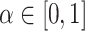 , the following significance rule
, the following significance rule
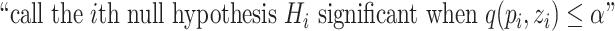 |
(2.9) |
has pFDR no larger than 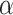 . Note that this significance rule is identical to the significance regions
. Note that this significance rule is identical to the significance regions 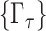 from above, so significance rule (2.9) also achieves the Bayes optimality for the loss function (2.7). We refer to (2.9) as the “Oracle”, which will be estimated by a procedure detailed below in Section 3. When only p-values
from above, so significance rule (2.9) also achieves the Bayes optimality for the loss function (2.7). We refer to (2.9) as the “Oracle”, which will be estimated by a procedure detailed below in Section 3. When only p-values 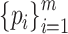 are used, the above significance rule becomes
are used, the above significance rule becomes
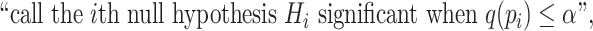 |
(2.10) |
where 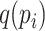 is the original q-value for
is the original q-value for 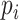 as developed in Storey (2002) and Storey (2003).
as developed in Storey (2002) and Storey (2003).
3. Implementation of the fFDR methodology
We aim to implement the decision rule in (2.9) for the fFDR methodology by a plug-in estimation procedure. For this, we need to estimate the two components of the statistic 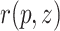 given in (2.4): the functional null proportion
given in (2.4): the functional null proportion 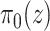 and the joint density
and the joint density 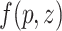 with support on
with support on 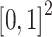 . We also need to estimate the q-value defined in (2.8). We will provide in Section 3.1 three complementary methods to estimate
. We also need to estimate the q-value defined in (2.8). We will provide in Section 3.1 three complementary methods to estimate 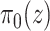 , in Section 3.2 a kernel-based method to estimate
, in Section 3.2 a kernel-based method to estimate 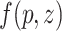 , and in Section 3.3 the estimation of q-values and the plug-in procedure.
, and in Section 3.3 the estimation of q-values and the plug-in procedure.
3.1. Estimating the functional null proportion
Our proposed approaches to estimate the functional null proportion 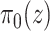 are based on an extension of the approach taken in Storey (2002). Recalling that
are based on an extension of the approach taken in Storey (2002). Recalling that 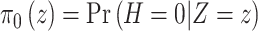 , it follows that for each
, it follows that for each 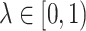 ,
,
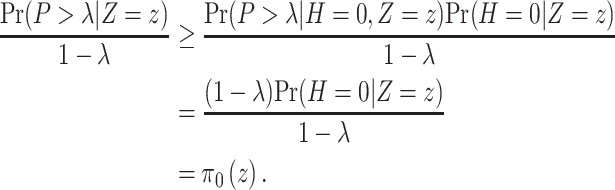 |
If we define the indicator function 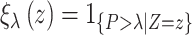 , then
, then
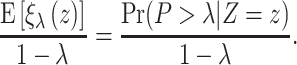 |
(3.11) |
Therefore, 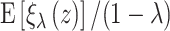 is a conservative estimate of
is a conservative estimate of 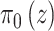 and it will form the basis of our estimate of
and it will form the basis of our estimate of 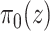 .
.
Our first method to estimate 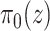 is referred to as the “GLM method” since it estimates
is referred to as the “GLM method” since it estimates 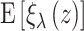 using generalized linear models (GLMs). For each
using generalized linear models (GLMs). For each 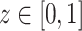 , we let
, we let 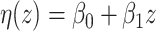 and
and
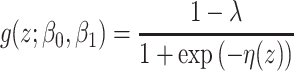 |
(3.12) |
for two parameters 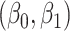 , and then fit
, and then fit
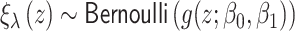 |
(3.13) |
to obtain an estimate 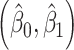 of
of 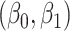 using the paired realizations
using the paired realizations 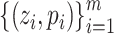 . We then estimate
. We then estimate 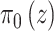 by
by
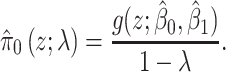 |
(3.14) |
Our second method to estimate 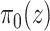 is referred to as the “GAM method” since it estimates
is referred to as the “GAM method” since it estimates 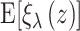 using generalized additive models (GAMs). Specifically, we model
using generalized additive models (GAMs). Specifically, we model 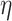 in the GLM method as a nonlinear function of
in the GLM method as a nonlinear function of 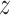 via GAM, while keeping the functional form of
via GAM, while keeping the functional form of 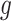 in (3.12) and the estimator (3.14). For example,
in (3.12) and the estimator (3.14). For example, 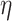 can be modeled by B-splines (Hastie and Tibshirani, 1986; Wahba, 1990) whose degree can be chosen, e.g., by generalized cross-validation (GCV) (Craven and Wahba, 1978). The GAM method removes the restriction induced by the GLM method that
can be modeled by B-splines (Hastie and Tibshirani, 1986; Wahba, 1990) whose degree can be chosen, e.g., by generalized cross-validation (GCV) (Craven and Wahba, 1978). The GAM method removes the restriction induced by the GLM method that 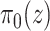 be a monotone function of
be a monotone function of 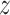 .
.
Our third method to estimate 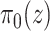 is referred to as the “Kernel method” since it estimates
is referred to as the “Kernel method” since it estimates 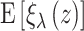 via kernel density estimation (KDE). Since
via kernel density estimation (KDE). Since 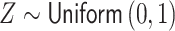 , it follows that
, it follows that
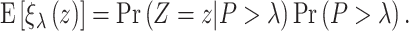 |
(3.15) |
To estimate 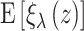 , we estimate the two factors in the right-hand side of (3.15) separately. It is straightforward to see that the estimator from Storey (2002),
, we estimate the two factors in the right-hand side of (3.15) separately. It is straightforward to see that the estimator from Storey (2002),
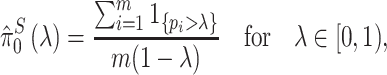 |
(3.16) |
is a conservative estimator of 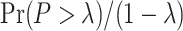 . Further, if we let
. Further, if we let 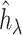 be a conservative estimator of the density of the
be a conservative estimator of the density of the 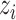 ’s whose corresponding p-values are greater than
’s whose corresponding p-values are greater than 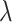 , then
, then 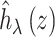 conservatively estimates
conservatively estimates 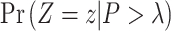 . Correspondingly,
. Correspondingly,
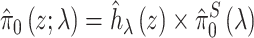 |
(3.17) |
is a conservative estimator of 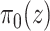 . In the implementation, we obtain
. In the implementation, we obtain 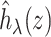 using the methods in Geenens (2014) since
using the methods in Geenens (2014) since 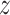 ranges in the unit interval. Note that (3.17) is essentially a nonparametric alternative to (3.14) since
ranges in the unit interval. Note that (3.17) is essentially a nonparametric alternative to (3.14) since 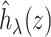 does not have the constraint on its shape that
does not have the constraint on its shape that 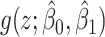 does.
does.
To maintain a concise notation, we write 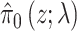 as
as 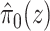 . If no information on the shape of
. If no information on the shape of 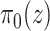 is available, we recommend using the Kernel or GAM method to estimate
is available, we recommend using the Kernel or GAM method to estimate 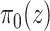 ; if
; if 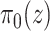 is monotonic in
is monotonic in 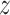 , then the GLM method is preferred. An approach for automatically handling the tuning parameter
, then the GLM method is preferred. An approach for automatically handling the tuning parameter 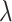 for the estimators is provided in Section 2 of the supplementary material available at Biostatistics online.
for the estimators is provided in Section 2 of the supplementary material available at Biostatistics online.
3.2. Estimating the joint density 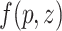
The estimation of the joint density 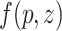 of the p-value
of the p-value 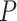 and informative variable
and informative variable 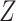 involves two challenges: (i)
involves two challenges: (i) 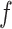 is a density function defined on the compact set
is a density function defined on the compact set 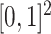 ; (ii)
; (ii) 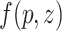 may be monotonic in
may be monotonic in 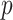 for each fixed
for each fixed 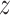 , requiring its estimate to also be monotonic. In fact, in the simulation study in Section 1 of the supplementary material available at Biostatistics online,
, requiring its estimate to also be monotonic. In fact, in the simulation study in Section 1 of the supplementary material available at Biostatistics online, 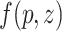 is monotonic in
is monotonic in 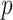 . To deal with these challenges, we estimate
. To deal with these challenges, we estimate 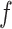 in a two-step procedure as follows. Firstly, to address the challenge of density estimation on a compact set, we use a local likelihood KDE method with a probit density transformation (Geenens, 2014) to obtain an estimate
in a two-step procedure as follows. Firstly, to address the challenge of density estimation on a compact set, we use a local likelihood KDE method with a probit density transformation (Geenens, 2014) to obtain an estimate 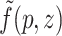 of
of 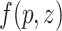 , where an adaptive nearest-neighbor bandwidth is chosen via GCV. Secondly, if
, where an adaptive nearest-neighbor bandwidth is chosen via GCV. Secondly, if 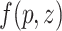 is known to be monotonic in
is known to be monotonic in 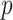 for each fixed
for each fixed 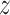 , then we utilize the algorithm in Section 3 of the supplementary material available at Biostatistics online to produce an estimated density
, then we utilize the algorithm in Section 3 of the supplementary material available at Biostatistics online to produce an estimated density 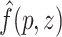 that has the same monotonicity property as
that has the same monotonicity property as 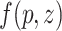 at the observations
at the observations 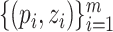 .
.
3.3. FDR and q-value estimation
With the estimates 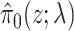 and
and 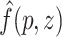 , respectively for
, respectively for 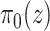 and
and 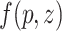 , the functional posterior error probability (or local FDR) statistic
, the functional posterior error probability (or local FDR) statistic 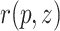 in (2.4) is estimated by
in (2.4) is estimated by
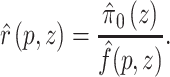 |
(3.18) |
For a threshold 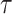 , Storey and others (2005) proposed the following pFDR estimate
, Storey and others (2005) proposed the following pFDR estimate
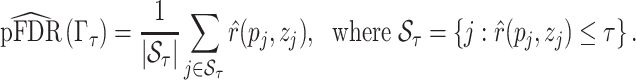 |
The rationale for this estimate is that the numerator is the expected number of false positives given the posterior distribution 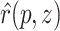 and the denominator is the expected number of total discoveries given
and the denominator is the expected number of total discoveries given 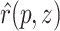 (which is directly observed). This is related to a semiparametric Bayesian procedure detailed in Newton and others (2004). Given this, the functional q-value
(which is directly observed). This is related to a semiparametric Bayesian procedure detailed in Newton and others (2004). Given this, the functional q-value 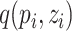 of
of 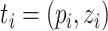 corresponding to the
corresponding to the 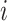 th null hypothesis
th null hypothesis 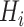 is estimated by:
is estimated by:
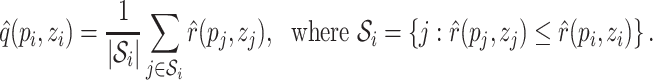 |
(3.19) |
The plug-in decision rule is to call the null hypothesis 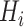 significant whenever
significant whenever 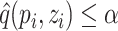 at a target pFDR level
at a target pFDR level 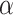 . In this work, we refer to this rule as the “functional FDR (fFDR) method”.
. In this work, we refer to this rule as the “functional FDR (fFDR) method”.
Recall that an estimate of 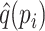 of the q-value
of the q-value 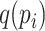 for
for 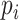 can be obtained by the q-value package (Storey and others, 2019). Then the plug-in decision rule based on
can be obtained by the q-value package (Storey and others, 2019). Then the plug-in decision rule based on 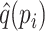 is to call the null hypothesis
is to call the null hypothesis 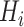 significant whenever
significant whenever 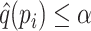 . This rule is referred to as the “standard FDR method” in this work. In Section 1 of the supplementary material available online at Biostatistics, we carry out a simulation study to demonstrate the accuracy of our estimator and compare its power to existing methods.
. This rule is referred to as the “standard FDR method” in this work. In Section 1 of the supplementary material available online at Biostatistics, we carry out a simulation study to demonstrate the accuracy of our estimator and compare its power to existing methods.
4. Applications in genomics
In this section, we apply the fFDR method to analyze data from two studies, one in a genetics of gene expression (eQTL) study on baker’s yeast and the other in an RNA-seq differential expression analysis on two inbred mouse strains. We will provide a brief background on the studies and then present the analysis results for both data sets.
4.1. Background on the eQTL experiment
The experiment on baker’s yeast (Sacchromyces cerevisiae) has been performed by Smith and Kruglyak (2008), where genome-wide gene expression was measured in each of the 109 genotyped strains under two conditions, glucose and ethanol. Here, we aim to identify genetic associations (technically, genetic linkage in this case) between pairings of expressed genes and SNPs among the samples grown on glucose. In this setting, the null hypothesis is “no association between a gene-SNP pair”, and the functional null proportion denotes the prior probability that the null hypothesis is true. The data set from this experiment is referred to as the “eQTL dataset”.
To keep the application straightforward, we consider only intra-chromosomal pairs, for which the genomic distances can be defined and are quantile normalized to give the informative variable 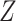 . (Note that the fFDR framework can be used to consider all gene–SNP pairs by estimating a standard
. (Note that the fFDR framework can be used to consider all gene–SNP pairs by estimating a standard 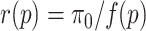 for all inter-chromosomal pairs and then combining these with the estimated
for all inter-chromosomal pairs and then combining these with the estimated 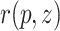 from the intra-chromosomal pairs to form the significance regions given in (2.6).) In this application, the genomic distance is calculated as the nucleotide basepair distance between the center of the gene and the SNP, the Wilcoxon test of association between gene expression and the allele at each SNP is used, and the p-values of such tests are obtained. We emphasize that the difference in the p-value histograms for the six strata shown in Figure 1a shows that a functional null proportion
from the intra-chromosomal pairs to form the significance regions given in (2.6).) In this application, the genomic distance is calculated as the nucleotide basepair distance between the center of the gene and the SNP, the Wilcoxon test of association between gene expression and the allele at each SNP is used, and the p-values of such tests are obtained. We emphasize that the difference in the p-value histograms for the six strata shown in Figure 1a shows that a functional null proportion 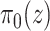 is more appropriate.
is more appropriate.
4.2. Background on the RNA-seq study
A common goal in gene expression studies is to identify genes that are differentially expressed across varying biological conditions. In RNA-seq based differential expression studies, this goal is to detect genes that are differentially expressed based on counts of reads mapped to each gene. The null hypothesis is “no differential expression (for a gene) between the two conditions”, and the functional null proportion denotes the prior probability that the null hypothesis is true. For an RNA-seq study, the quantile normalized per-gene read depth is the informative variable 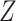 that we utilized, which affects the power of the involved test statistics (Tarazona and others, 2011) or the prior probability of differential expression (Robinson and others, 2015).
that we utilized, which affects the power of the involved test statistics (Tarazona and others, 2011) or the prior probability of differential expression (Robinson and others, 2015).
We utilized the RNA-seq data studied in Bottomly and others (2011), due to its availability in the ReCount database (Frazee and others, 2011) and because it had previously been examined in a comparison of differential expression methods (Soneson and Delorenzi, 2013). The data set, referred to as the “RNA-seq dataset”, contains 102.98 million mapped RNA-seq reads in 21 individuals from two inbred mouse strains. As proposed in Law and others (2014), we normalized the data using the voom R package, fitted a weighted linear least squares model to each gene expression variable, and then obtained a p-value for each gene based on a t-test of the coefficient corresponding to mouse strain.
4.3. Estimating the functional null proportion in the two studies
We applied to these two data sets our estimator 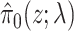 of the functional null proportion
of the functional null proportion 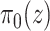 utilizing the GLM, GAM, and Kernel methods. Figure 2 shows
utilizing the GLM, GAM, and Kernel methods. Figure 2 shows 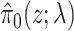 for these two data sets, and the tuning parameter
for these two data sets, and the tuning parameter 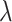 has been chosen to be the one that minimizes the mean integrated squared error of the function
has been chosen to be the one that minimizes the mean integrated squared error of the function 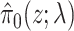 ; see Section 2 of the supplementary material available at Biostatistics online for details on choosing
; see Section 2 of the supplementary material available at Biostatistics online for details on choosing 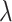 . In both data sets,
. In both data sets, 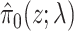 based on the GAM and Kernel methods give very similar estimates, with the one based on the GLM method more distinct, likely because the latter puts stricter constraints on the shape of
based on the GAM and Kernel methods give very similar estimates, with the one based on the GLM method more distinct, likely because the latter puts stricter constraints on the shape of 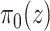 . By comparing Figure 2 to the results in Figure 4 (for estimating a constant
. By comparing Figure 2 to the results in Figure 4 (for estimating a constant 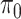 ) of the supplementary material available at Biostatistics online, we see that in this RNA-seq study the read depths appear to affect the prior probability of differential expression,
) of the supplementary material available at Biostatistics online, we see that in this RNA-seq study the read depths appear to affect the prior probability of differential expression, 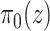 .
.
Fig. 2.
Estimate 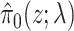 of the functional null proportion
of the functional null proportion 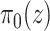 for the eQTL and RNA-seq studies, using the GLM, GAM, or Kernel method. Each plot shows the estimate
for the eQTL and RNA-seq studies, using the GLM, GAM, or Kernel method. Each plot shows the estimate 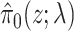 for different values of the tuning parameter
for different values of the tuning parameter 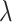 , where the solid curve corresponds to the chosen tuning parameter value. The tuning parameter is chosen to balance the trade-off between the integrated bias and variance of the function
, where the solid curve corresponds to the chosen tuning parameter value. The tuning parameter is chosen to balance the trade-off between the integrated bias and variance of the function 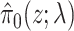 ; details on how to choose
; details on how to choose 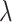 are given in Section 2 of the supplementary material available at Biostatistics online.
are given in Section 2 of the supplementary material available at Biostatistics online.
As expected, the estimator 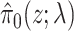 for the eQTL data set increases with genomic distance, indicating that a distal gene–SNP association is less likely than local association. Using the GAM and Kernel methods,
for the eQTL data set increases with genomic distance, indicating that a distal gene–SNP association is less likely than local association. Using the GAM and Kernel methods, 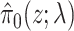 ranges from about
ranges from about 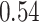 for very local associations to about
for very local associations to about 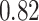 for distant gene–SNP pairs. In the RNA-seq data set,
for distant gene–SNP pairs. In the RNA-seq data set, 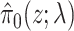 obtained by the GAM and Kernel methods decreases from around
obtained by the GAM and Kernel methods decreases from around 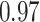 to around
to around 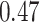 as read depth increases.
as read depth increases.
In the eQTL data set, 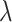 values from
values from 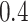 to
to 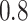 led to very similar shapes of
led to very similar shapes of  (see Figure 2), and the integrated bias of
(see Figure 2), and the integrated bias of 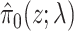 is always low compared with its integrated variance, leading to the choice of
is always low compared with its integrated variance, leading to the choice of 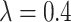 for all three methods. This likely indicates that the test statistics implemented in this experiment have high power, leading to low bias in estimating
for all three methods. This likely indicates that the test statistics implemented in this experiment have high power, leading to low bias in estimating 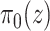 . In contrast, in the RNA-seq data set, the integrated bias of
. In contrast, in the RNA-seq data set, the integrated bias of 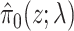 does decrease as
does decrease as 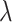 increases, leading to a choice of a higher
increases, leading to a choice of a higher 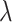 . While the choice of
. While the choice of 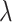 for
for 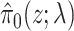 may deserve further study, it is clear from these applications that the choice of
may deserve further study, it is clear from these applications that the choice of 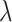 has a small effect on
has a small effect on 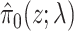 and that it is beneficial to employ a functional
and that it is beneficial to employ a functional 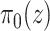 of the informative variable rather than a constant
of the informative variable rather than a constant 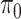 .
.
4.4. Application of fFDR method in the two studies
For the eQTL analysis described in Section 4.1, 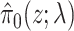 based on the GAM method is used (see Figure 2), and the fFDR method is applied to the p-values of the tests of associations and the quantile normalized genomic distances. At the target FDR of
based on the GAM method is used (see Figure 2), and the fFDR method is applied to the p-values of the tests of associations and the quantile normalized genomic distances. At the target FDR of 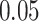 , the fFDR method found
, the fFDR method found 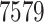 associated gene–SNP pairs, the standard FDR method
associated gene–SNP pairs, the standard FDR method 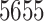 , and the two methods shared
, and the two methods shared 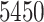 discoveries. Figure 3a shows that, at all target FDR levels, the fFDR method has higher power than the standard FDR method. In addition, Figure 3b reveals that the significance region of the fFDR method is greatly influenced by the gene–SNP distance, as the p-value cutoff for significance is higher for close gene–SNP pairs and lower for distant gene–SNP pairs. This, together with Figure 3c, means that some q-values
discoveries. Figure 3a shows that, at all target FDR levels, the fFDR method has higher power than the standard FDR method. In addition, Figure 3b reveals that the significance region of the fFDR method is greatly influenced by the gene–SNP distance, as the p-value cutoff for significance is higher for close gene–SNP pairs and lower for distant gene–SNP pairs. This, together with Figure 3c, means that some q-values 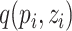 for the fFDR method can be larger than the q-values
for the fFDR method can be larger than the q-values 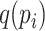 of the standard FDR method. Thus, the use of an informative variable by the fFDR method changes the significance ranking of the null hypotheses and increases the power of multiple testing at the same target FDR level.
of the standard FDR method. Thus, the use of an informative variable by the fFDR method changes the significance ranking of the null hypotheses and increases the power of multiple testing at the same target FDR level.
Fig. 3.
The fFDR method applied for multiple testing in the eQTL and RNA-seq analyses. (a) Number of significant hypothesis tests at various target FDRs. The fFDR method (func FDR) has more significant tests than the standard FDR method (std FDR) at all target FDRs. (b) The significance regions of the fFDR method for various target FDRs, indicated by scatter plots of the p-values and informative variable. The horizontal lines indicate the significance thresholds that would be used by the standard FDR method at the same target FDRs. Clearly, these lines do not take the informative variable into account. (c) A scatter plot comparing the q-values for the standard FDR method (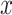 axis) to the q-values for the fFDR method (
axis) to the q-values for the fFDR method (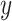 axis), colored based on the informative variable
axis), colored based on the informative variable 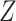 with reference line
with reference line 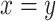 in red. It is clear that the fFDR method re-ranks the significance of hypotheses tests.
in red. It is clear that the fFDR method re-ranks the significance of hypotheses tests.
For the RNA-seq analysis, the estimator 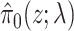 based on the GAM method is used (see Figure 2), and the fFDR method is applied to the p-values of the tests for differential expression and the quantiles of the read depths. Similar to the eQTL analysis, the fFDR method has a larger number of significant hypothesis tests at all target FDR levels; see Figure 3a. At the target FDR of
based on the GAM method is used (see Figure 2), and the fFDR method is applied to the p-values of the tests for differential expression and the quantiles of the read depths. Similar to the eQTL analysis, the fFDR method has a larger number of significant hypothesis tests at all target FDR levels; see Figure 3a. At the target FDR of 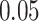 , the fFDR method found
, the fFDR method found 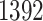 genes to be differentially expressed, while the standard FDR method found
genes to be differentially expressed, while the standard FDR method found 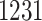 , and the two methods shared
, and the two methods shared 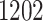 discoveries. In this RNA-seq analysis, the fFDR method has a smaller improvement in power (see Figure 3a), the differences between the q-values for the fFDR method and those for the standard FDR method are smaller (see Figure 3c), and the significance region of the fFDR method is less affected by the informative variable
discoveries. In this RNA-seq analysis, the fFDR method has a smaller improvement in power (see Figure 3a), the differences between the q-values for the fFDR method and those for the standard FDR method are smaller (see Figure 3c), and the significance region of the fFDR method is less affected by the informative variable 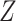 (see Figure 3b). This may be because the total number of differentially expressed genes in the RNA-seq study was small or the test statistics applied in this experiment were already powerful.
(see Figure 3b). This may be because the total number of differentially expressed genes in the RNA-seq study was small or the test statistics applied in this experiment were already powerful.
5. Discussion
We have proposed the fFDR methodology to utilize additional information on the prior probability of a null hypothesis being true or the power of the family of test statistics in multiple testing. It employs a functional null proportion of true null hypotheses and a joint density for the p-values and informative variable. Our simulation studies have demonstrated that the fFDR methodology is more accurate and informative than the standard FDR method, that the former does not perform worse than the latter when the informative variable is in fact non-informative, and that the fFDR methodology is more powerful than the IHW method. (see Section 1 of the supplementary material available at Biostatistics online).
Besides the eQTL and RNA-seq analyses demonstrated here, the fFDR methodology is applicable to multiple testing in other studies. For example, it can be applied to genome-wide association studies such as those conducted in Dalmasso and others (2008) and Roeder and others (2006), where an informative variable can incorporate differing minor allele frequencies or information on the prior probability of a gene–SNP association obtained from previous genome linkage scans. It can also be used in brain imaging studies, e.g., those conducted or reviewed in Benjamini and Heller (2007) and Chumbley and Friston (2009), to integrate as the informative variable spatial-temporal information on the voxel measurements.
We recommend using domain knowledge to determine and choose an informative variable. In essence, any random variable that does not affect the null distribution of p-value is a legitimate candidate for an informative variable. On the other hand, when the informative variable is actually non-informative on the prior of a null hypothesis being true or the power of an individual test, the fFDR method reduces to the standard FDR method, and there is no loss of power employing the fFDR method (compared with the standard FDR method). It would also be useful to develop a formal statistical test to check if a random variable is informative.
Finally, the fFDR methodology can be extended to the case where p-values or the status of null hypotheses are dependent on each other. In this setting, the corresponding decision rule may be different from that obtained here. On the other hand, the methodology can be extended to incorporate a vector of informative variables. This could be especially appropriate when additional information cannot be compressed into a univariate informative variable. Briefly, let 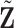 be a
be a 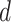 -dimensional random vector. We can transform
-dimensional random vector. We can transform 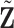 into
into 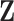 such that
such that 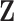 is approximately uniformly distributed on the
is approximately uniformly distributed on the 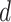 -dimensional unit cube
-dimensional unit cube 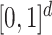 . Assume
. Assume  and maintain the notation for p-value and status of a hypothesis used in Section 2. Then the extended model has the following components: (i)
and maintain the notation for p-value and status of a hypothesis used in Section 2. Then the extended model has the following components: (i) 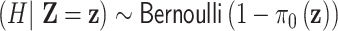 , where the function
, where the function 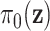 ranges in
ranges in 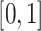 ; (ii) when the null hypothesis is true,
; (ii) when the null hypothesis is true, 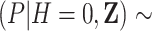 Uniform(0,1) regardless of the value of
Uniform(0,1) regardless of the value of 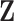 ; (iii) when the null hypothesis is false, the conditional density of
; (iii) when the null hypothesis is false, the conditional density of 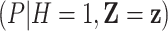 is
is 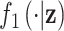 . Consequently, the conditional density of
. Consequently, the conditional density of 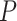 given
given 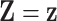 is
is 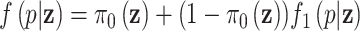 , and the joint density
, and the joint density 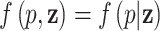 for all
for all 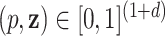 . The estimation procedures and significance rule we have proposed can be extended accordingly.
. The estimation procedures and significance rule we have proposed can be extended accordingly.
6. Software
The methods described in this article are available in the fFDR R package, available at https://github.com/StoreyLab/fFDR (most recent version), which will also be made available on CRAN.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Funding
This research was supported in part by National Institutes of Health [R01 HG002913 and R01 HG006448] and Office of Naval Research [N00014-12-1-0764].
References
- Benjamini, Y. and Heller, R. (2007). False discovery rates for spatial signals. Journal of the American Statistical Association 102, 1272–1281. [Google Scholar]
- Benjamini, Y. and Hochberg, Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B 57, 289–300. [Google Scholar]
- Boca, S. M. and Leek, J. T. (2018). A direct approach to estimating false discovery rates conditional on covariates. PeerJ 6: e6035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bottomly, D., Walter, N. A. R., Hunter, J. E., Darakjian, P., Kawane, S., Buck, K. J., Searles, R. P., Mooney, M., McWeeney, S. K. and Hitzemann, R. (2011). Evaluating gene expression in C57BL/6J and DBA/2J mouse striatum using RNA-Seq and microarrays. PLoS One 6, e17820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brem, R. B., Yvert, G., Clinton, R. and Kruglyak, L. (2002). Genetic dissection of transcriptional regulation in budding yeast. Science 296, 752–755. [DOI] [PubMed] [Google Scholar]
- Cai, G., Li, H., Lu, Y., Huang, X., Lee, J., Müller, P., Ji, Y. and Liang, S. (2012). Accuracy of RNA-Seq and its dependence on sequencing depth. BMC Bioinformatics 13, S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai, T. T. and Sun, W. (2009). Simultaneous testing of grouped hypotheses: finding needles in multiple haystacks. Journal of the American Statistical Association 104, 1467–1481. [Google Scholar]
- Chumbley, J. and Friston, K. (2009). False discovery rate revisited: FDR and topological inference using Gaussian random fields. Neuroimage 44, 62–70. [DOI] [PubMed] [Google Scholar]
- Craven, P. and Wahba, G. (1978). Smoothing noisy data with spline functions. Numerische Mathematik 31, 377–403. [Google Scholar]
- Dalmasso, C., Génin, E. and Trégouet, D.-A. (2008). A weighted-Holm procedure accounting for allele frequencies in genomewide association studies. Genetics 180, 697–702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doss, S., Schadt, E. E., Drake, T. A. and Lusis, A. J. (2005). Cis-acting expression quantitative trait loci in mice. Genome Research 15, 681–691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron, B., Tibshirani, R., Storey, J. D. and Tusher, V. (2001). Empirical Bayes analysis of a microarray experiment. Journal of the American Statistical Association 96, 1151–1160. [Google Scholar]
- Frazee, A. C., Langmead, B. and Leek, J. T. (2011). ReCount: a multi-experiment resource of analysis-ready RNA-seq gene count datasets. BMC Bioinformatics 12, 449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geenens, G. (2014). Probit transformation for nonparametric kernel estimation on the unit interval. Journal of the American Statistical Society 109, 346–358. [Google Scholar]
- Genovese, C. R., Roeder, K. and Wasserman, L. (2006). False discovery control with p-value weighting. Biometrika 93, 509–524. [Google Scholar]
- Hastie, T. and Tibshirani, R. (1986). Generalized additive models. Statistical Science 1, 297–310. [DOI] [PubMed] [Google Scholar]
- Hu, J. X., Zhao, H. and Zhou, H. H. (2010). False discovery rate control with groups. Journal of the American Statistical Association 105, 1215–1227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ignatiadis, N. and Huber, W. (2018). Covariate powered cross-weighted multiple testing with false discovery rate control. arXiv:1701.05179. [Google Scholar]
- Ignatiadis, N., Klaus, B., Zaugg, J. B. and Huber, W. (2016). Data-driven hypothesis weighting increases detection power in genome-scale multiple testing. Nature Methods 13, 577–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kall, L., Storey, J. D., MacCoss, M. J. and Noble, W. S. (2008). Posterior error probabilities and false discovery rates: two sides of the same coin. Journal of Proteome Research 7, 40–44. [DOI] [PubMed] [Google Scholar]
- Law, C. W., Chen, Y., Shi, W. and Smyth, G. K. (2014). Voom: precision weights unlock linear model analysis tools for RNA-seq read counts. Genome Biology 15, R29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newton, M. A., Noueiry, A., Sarkar, D. and Ahlquist, P. (2004). Detecting differential gene expression with a semiparametric hierarchical mixture method. Biostatistics (Oxford, England) 5, 155–176. [DOI] [PubMed] [Google Scholar]
- Ochoa, A., Storey, J. D., Llinás, M. and Singh, M. (2015). Beyond the E-value: stratified statistics for protein domain prediction. PLoS Computational Biology 11, e1004509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson, D. G., Wang, J. Y. and Storey, J. D. (2015). A nested parallel experiment demonstrates differences in intensity-dependence between rna-seq and microarrays. Nucleic Acids Research 43, e131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roeder, K., Bacanu, S.-A., Wasserman, L. and Devlin, B. (2006). Using linkage genome scans to improve power of association in genome scans. American Journal of Human Genetics 78, 243–252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ronald, J., Brem, R. B., Whittle, J. and Kruglyak, L. (2005). Local regulatory variation in Saccharomyces cerevisiae. PLoS Genetics 1, e25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roquain, E. and van de Wiel, M. A. (2009). Optimal weighting for false discovery rate control. Electronic Journal of Statistics 3, 678–711. [Google Scholar]
- Scott, J. G., Kelly, R. C., Smith, M. A., Zhou, P. and Kass, R. E. (2015). False discovery rate regression: An application to neural synchrony detection in primary visual cortex. Journal of the American Statistical Association 110, 459–471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, E. N. and Kruglyak, L. (2008). Gene-environment interaction in yeast gene expression. PLoS Biology 6, e83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soneson, C. and Delorenzi, M. (2013). A comparison of methods for differential expression analysis of RNA-seq data. BMC Bioinformatics 14, 91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey, J. D. (2002). A direct approach to false discovery rates. Journal of the Royal Statistical Society, Series B 64, 479–498. [Google Scholar]
- Storey, J. D. (2003). The positive false discovery rate: a Bayesian intepretation and the q-value. Annals of Statistics 3, 2013–2035. [Google Scholar]
- Storey, J. D., Akey, J. M. and Kruglyak, L. (2005). Multiple locus linkage analysis of genomewide expression in yeast. PLoS Biology 3, e267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey, J. D., Bass, A. J., Dabney, A. R. and Robinson, D. (2019). qvalue: Q-value Estimation for False Discovery Rate Control. R package version 2.16.0 [Google Scholar]
- Sun, L., Craiu, R. V., Paterson, A. D. and Bull, S. B. (2006). Stratified false discovery control for large-scale hypothesis testing with application to genome-wide association studies. Genetic Epidemiology 30, 519–530. [DOI] [PubMed] [Google Scholar]
- Tarazona, S., García-Alcalde, F., Dopazo, J., Ferrer, A. and Conesa, A. (2011). Differential expression in RNA-seq: a matter of depth. Genome Research 21, 2213–2223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wahba, G. (1990). Spline Models for Observational Data. CBMS-NSF Regional Conference Series in Applied Mathematics (Book 59) SIAM: Society for Industrial and Applied Mathematics; Philadelphia, PA. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.