Summary
The goal of expression quantitative trait loci (eQTL) studies is to identify the genetic variants that influence the expression levels of the genes in an organism. High throughput technology has made such studies possible: in a given tissue sample, it enables us to quantify the expression levels of approximately 20 000 genes and to record the alleles present at millions of genetic polymorphisms. While obtaining this data is relatively cheap once a specimen is at hand, obtaining human tissue remains a costly endeavor: eQTL studies continue to be based on relatively small sample sizes, with this limitation particularly serious for tissues as brain, liver, etc.—often the organs of most immediate medical relevance. Given the high-dimensional nature of these datasets and the large number of hypotheses tested, the scientific community has adopted early on multiplicity adjustment procedures. These testing procedures primarily control the false discoveries rate for the identification of genetic variants with influence on the expression levels. In contrast, a problem that has not received much attention to date is that of providing estimates of the effect sizes associated with these variants, in a way that accounts for the considerable amount of selection. Yet, given the difficulty of procuring additional samples, this challenge is of practical importance. We illustrate in this work how the recently developed conditional inference approach can be deployed to obtain confidence intervals for the eQTL effect sizes with reliable coverage. The procedure we propose is based on a randomized hierarchical strategy with a 2-fold contribution: (1) it reflects the selection steps typically adopted in state of the art investigations and (2) it introduces the use of randomness instead of data-splitting to maximize the use of available data. Analysis of the GTEx Liver dataset (v6) suggests that naively obtained confidence intervals would likely not cover the true values of effect sizes and that the number of local genetic polymorphisms influencing the expression level of genes might be underestimated.
Keywords: Conditional inference, Confidence intervals, Effect size estimation, eQTL, Randomization, Selection bias, Winner’s curse
1. Introduction
The goal of an expression quantitative trait loci (eQTL) study is to identify the genetic variants that regulate the expression of genes in different biological contexts and quantify their effects. Using statistical terminology, the outcome variables (typically on the order of 20 000) are molecular measurements of the gene expression and the predictors are genotypes for single nucleotide polymorphisms (SNP; typically on the order of 1 000 000). The variants that are discovered to regulate gene expression are referred as eVariants and careful estimation of their effect sizes is often deferred to follow-up studies. One commonly studied sub-type of eVariants are those referred to as cis-eQTL: the DNA variants in the neighborhood of a gene that influence its expression directly. The majority of eQTL investigations have focused on detecting these cis variants owing to their simple biological interpretation as well as the fact that restricting attention to this subset of gene and variant pairs reduces the number of tested hypotheses and leads to improved power. Still, when concentrating on cis regulation, eQTL studies face a formidable multiplicity problem and also, a subsequent winner’s curse during effect size estimation of discovered associations, with approximately 20 000 genes and an average of 7500 variants in each cis region.
Since the first studies (Schadt and others, 2003), the eQTL research community has recognized the false discovery rate (FDR) as a relevant global error rate and adopted corresponding controlling strategies. As the density of SNP genotyping increased over time, it became apparent that naive application of FDR controlling strategies (Benjamini and Hochberg, 1995; Storey, 2003) might lead to excessive false discoveries. To address this difficulty, more recent works (Ongen and others, 2015; Lonsdale and others, 2013) adopt a hierarchical strategy. First, for each gene one tests the null hypothesis of no association with any local variants and the p-values corresponding to these tests are passed to an FDR controlling procedure. Second, for those genes for which this null is rejected (eGenes), scientists proceed to identify which among the cis variants have an effect (eVariants). To this end, both marginal testing and multivariate regression models have been used to report the cis variants with significant association with eGenes.
Once eVariants have been detected, the logical next step is to attempt to estimate their effect sizes; and given the scarcity of biological samples, it is tempting to do so using the data at hand. However, since these discoveries have been selected out of a large number of possible associations, naive estimators based on the same data used for selection would result in inaccurate estimates. Indeed, this is a situation similar to that of genome-wide association study, where this problem of “winner’s curse” has been noted before (Zhong and Prentice, 2008). One clear way out, of course, is offered by the classical concept of data-splitting. However, in settings where the sample size is already small, reserving a hold-out data set for inference is beyond affordability. This is often the case in human eQTL studies: for tissues other than the easily accessible blood and skin, the relations between 20 000 genes and millions of SNPs are typically studied with a number of specimens in the hundreds at best. The same difficulties that lead to small sample sizes, make it unrealistic to simply defer the task of estimating effects to a new dataset. In this work, we explore the potential for this problem in light of recent developments in the statistical literature: specifically, the notion of conditional inference after selection and the power of randomization strategies. We offer a pipeline for the identification of eVariants and estimation of their effect sizes that mimics the hierarchical analysis, representing the state of the art in eQTL studies. Comparing the results of our pipeline with alternative strategies in simulations and real data analysis helps us understand the severity of the challenges of inference after selection in the context of eQTL. Our contribution supports investigators in their choice of optimal use of limited samples in a single study, balancing the need to efficiently discover relations with that of making inference on the effect sizes of the discoveries.
1.1. Approach: a randomized conditional perspective
Our methods build upon a conditional inference perspective, introduced in Lee and others (2016). The central idea is that, to counter selection bias, inference on the parameters (effect sizes, in the case of eQTL analysis) should be based on an adjusted likelihood, obtained by conditioning the data generative model on the selection event. Conditioning has the effect of discarding the information in the data used in selecting the eVariants, so that effect sizes are estimated on “unused data.” In addition, we capitalize on the observation that it is possible to generalize data-splitting in a manner that allows one to make a more efficient use of the information in the sample by introducing randomization during selection (Tian and others, 2018).
The 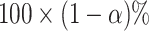 selection-adjusted confidence intervals are such that the probability with which each of them does not cover its target population parameter is at most
selection-adjusted confidence intervals are such that the probability with which each of them does not cover its target population parameter is at most 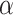 , conditional on selection. This guarantee is first described in Lee and others (2016), where it is called selective false-coverage rate control. As a point estimator, we employ the maximum likelihood estimator (MLE) calculated from the conditional law, introduced in Panigrahi and others (2016). We call this estimator the selection-adjusted MLE: this serves as a quantification of the strengths of the discovered associations.
, conditional on selection. This guarantee is first described in Lee and others (2016), where it is called selective false-coverage rate control. As a point estimator, we employ the maximum likelihood estimator (MLE) calculated from the conditional law, introduced in Panigrahi and others (2016). We call this estimator the selection-adjusted MLE: this serves as a quantification of the strengths of the discovered associations.
We follow the introduction with examples of the challenges presented by selection and of how the conditional inference approach addresses them in Section 2: this gives us the opportunity to introduce terminology as well as to discuss the concepts of randomization, target of inference, and statistical model in this context. The rest of the article deals with the more complicated hierarchical setting of eQTL research, which requires novel methodological results and is organized as follows. Section 3 describes the randomized selection pipeline that we employ as the eQTL identification strategy; Section 4 presents our proposal for selection-adjusted inference; Section 5 contains the results of a simulation study and the concluding section presents the analysis of data from GTEx.
2. Motivating examples
While the substantial contribution of the present work is to design a selection and inference pipeline that adapts to the hierarchical strategy typically adopted in eQTL studies, we start by considering a couple of “cartoon” examples that illustrate the effect of selection bias and motivate the overall sprit of our strategy, bypassing the complications associated to eGene selection. We focus on one gene, and imagine that the entire goal of the study is to find which of its cis variants influence its expression and with what effect sizes. We consider two selection strategies: the first (1) consists in choosing the DNA variant that is most strongly associated with the gene (see Ongen and others 2015); the second (2) uses the LASSO to identify a set of variants. In both cases, we are interested in inferring the effect sizes of the selected variants.
Introducing some notation, let 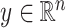 be the response and
be the response and 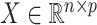 be a matrix collecting the values of predictors. Assume, without any loss of generality, that
be a matrix collecting the values of predictors. Assume, without any loss of generality, that 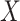 is both centered and scaled to have columns of norm
is both centered and scaled to have columns of norm 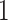 . Strategy (1) identifies the variant with the greatest marginal t-statistic. Let this variant correspond to the
. Strategy (1) identifies the variant with the greatest marginal t-statistic. Let this variant correspond to the 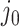 th column of
th column of 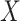 , denoted as
, denoted as 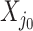 which satisfies
which satisfies 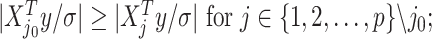
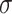 being the noise-variance in the outcome variable, here assumed known. For strategy (2), we consider a LASSO selection with a small ridge penalty
being the noise-variance in the outcome variable, here assumed known. For strategy (2), we consider a LASSO selection with a small ridge penalty  (for numerical stability) given by
(for numerical stability) given by 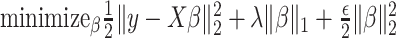 . We choose the tuning parameter as
. We choose the tuning parameter as 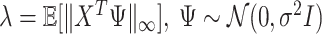 , a theoretical value adopted from Negahban and others (2009).
, a theoretical value adopted from Negahban and others (2009).
We will be introducing randomization schemes for both strategies, which perturb the selection with the addition of some Gaussian noise 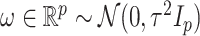 . Specifically, the randomized version of strategy (1) leads to the identification of variant
. Specifically, the randomized version of strategy (1) leads to the identification of variant 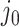 when it satisfies:
when it satisfies: 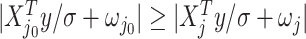
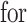
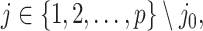 and the randomized version of strategy (2) solves the following modified optimization problem:
and the randomized version of strategy (2) solves the following modified optimization problem: 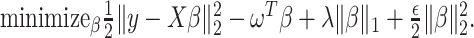
2.1. Model and target
For the problem of inference following these selections, we note that we need to (a) specify a model for the data with respect to which evaluate the properties of estimators and (b) we need to formally identify the target parameters. Of course, (a) is challenging in a context of model selection, where by definition we do not know what is the “true” model. Nevertheless it makes sense to work with what we might term the “full model,” where mean of response variable 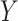 is parameterized by a
is parameterized by a 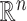 vector
vector 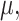 without specifying a relation with
without specifying a relation with 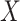 and
and 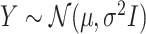 : this is also the choice made in Berk and others (2013); Lee and others (2016).
: this is also the choice made in Berk and others (2013); Lee and others (2016).
While this full model allows us to talk precisely about the distribution of 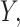 the target of inference (b) in both these examples is not
the target of inference (b) in both these examples is not 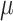 , but depends on the outcome of selection. This adaptive target can be described as the projection of
, but depends on the outcome of selection. This adaptive target can be described as the projection of 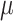 on the space spanned by the selected variables. For the marginal example, the adaptive target is given by
on the space spanned by the selected variables. For the marginal example, the adaptive target is given by 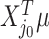 . Denoting
. Denoting 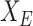 as the selected sub-matrix, this target for the LASSO is given by
as the selected sub-matrix, this target for the LASSO is given by 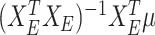 , the partial regression coefficients that are obtained by fitting a linear model to the selected set of variables
, the partial regression coefficients that are obtained by fitting a linear model to the selected set of variables 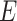 .
.
2.2. Methods
We are now ready to explore via simulations the performance of four different inferential methods. The first (i) is “Vanilla” inference that ignores selection and relies on the estimates for the adaptive targets that one would use if these were specified in advance: in the first example, this is simply the largest t-statistic, and for the second example, this is the least squared estimator with the corresponding intervals centered around these point estimates. Second, (ii) we consider the adjusted inference described in Lee and others (2016) (“Lee et al.”) which corrects for selection bias based on a screening without randomization [note that Lee and others (2016) does not provide a selection-adjusted point estimate, but gives a recipe for confidence intervals]. The third approach (iii) is in the spirit of the methods we develop in the rest of the article: we condition on the outcome of randomized selection and provide adjusted confidence intervals and point estimates (“Proposed”). Finally, to provide a benchmark comparison with a more well-adopted practice of data-splitting, and (iv) we include the method of splitting (“Split”) that computes selection on a random fraction of the data and uses the remaining samples for inference.
2.3. Simulations
In our simulations, 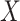 is fixed and a response vector
is fixed and a response vector 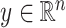 is generated in each round from
is generated in each round from 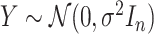 ,
, 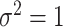 , independently of
, independently of 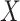 . The perturbation
. The perturbation 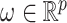 is generated from
is generated from 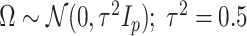 , independently of
, independently of 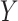 . We simulate
. We simulate 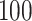 such instances and compare the inferential procedures in terms of coverage, length of the confidence intervals, and risk of the point estimates. The risk metric we use is the averaged squared error deviation of the point estimates from the respective adaptive targets, described above for the two selection strategies. To implement splitting, we consider a split of data that is directly comparable to our randomization scheme. Formalized in Panigrahi (2018), data-splitting is equivalent to a randomized selection with the randomization variance
such instances and compare the inferential procedures in terms of coverage, length of the confidence intervals, and risk of the point estimates. The risk metric we use is the averaged squared error deviation of the point estimates from the respective adaptive targets, described above for the two selection strategies. To implement splitting, we consider a split of data that is directly comparable to our randomization scheme. Formalized in Panigrahi (2018), data-splitting is equivalent to a randomized selection with the randomization variance 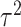 corresponding to
corresponding to 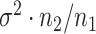 , where
, where 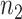 and
and 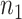 are the number of samples used for inference and selection, respectively;
are the number of samples used for inference and selection, respectively; 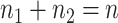 . Thus, in the comparisons that follow, we choose the splitting ratio for “Split” as
. Thus, in the comparisons that follow, we choose the splitting ratio for “Split” as 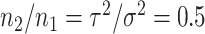 ;
;  and
and 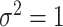 .
.
2.4. Results and insights
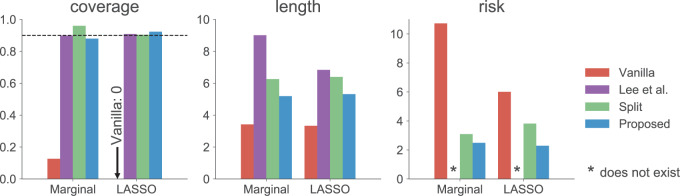
The results are summarized in Figure 1. As expected, the unadjusted intervals based on “Vanilla” inference fall way short of coverage highlighting the extent of “winner’s curse.” The adjusted intervals from “Split” inference and in the form described in Lee and others (2016) and in the present work, based on randomization, all achieve the target coverage. These adjusted methods, however, differ in terms of interval length: while the “Proposed” intervals are 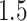 times longer than the unadjusted intervals (a price we pay for selection), they are much shorter than the exact intervals post non-randomized screenings in Lee and others (2016) and the “Split” intervals. This is the advantage of randomization at the selection stage: there is more “left-over” information available at the time of inference. The risks of the “Vanilla” and “Split” point-estimate post a non-randomized screening is also seen to be higher than the adjusted MLE, considered as a point estimate for effect sizes in this article.
times longer than the unadjusted intervals (a price we pay for selection), they are much shorter than the exact intervals post non-randomized screenings in Lee and others (2016) and the “Split” intervals. This is the advantage of randomization at the selection stage: there is more “left-over” information available at the time of inference. The risks of the “Vanilla” and “Split” point-estimate post a non-randomized screening is also seen to be higher than the adjusted MLE, considered as a point estimate for effect sizes in this article.
Fig. 1.
The left most panel compares the coverages of the confidence intervals, where the dotted black line represents the target 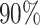 coverage. The central panel in the plot gives an indication of the power of statistical inference through lengths of these intervals. Finally, the right most panel compares the empirical risks of the adjusted and unadjusted point estimates with respect to a squared error loss. On the
coverage. The central panel in the plot gives an indication of the power of statistical inference through lengths of these intervals. Finally, the right most panel compares the empirical risks of the adjusted and unadjusted point estimates with respect to a squared error loss. On the 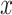 -axes, “Marginal” denotes the inference following selection strategy (1): a marginal screening analysis based on a marginal t-statistic; and “LASSO” indicates the inferential results following selection strategy (2): screenings by LASSO. The performances of the four inferential strategies compared are indicated using different colors, as in the legend.
-axes, “Marginal” denotes the inference following selection strategy (1): a marginal screening analysis based on a marginal t-statistic; and “LASSO” indicates the inferential results following selection strategy (2): screenings by LASSO. The performances of the four inferential strategies compared are indicated using different colors, as in the legend.
Additionally, we provide in Figure 1 of supplementary material available at Biostatistics online comparisons between an equivalent “Split” and “Proposed” at different scales of randomization and an equivalent split proportion. The critical take-away from this analysis is a uniform domination in inferential powers in adopting our proposal over the prevalent approach of splitting. In inferring about the adaptive target post-selection, “Proposed” interval estimates are shorter than “Split” by roughly  at split proportions
at split proportions 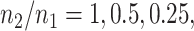 respectively. Consistent with expectations of an efficient utilization of left-over information from the selection stage, this gain in inferential power becomes more pronounced as more data are used for selection, leaving lesser information for inference.
respectively. Consistent with expectations of an efficient utilization of left-over information from the selection stage, this gain in inferential power becomes more pronounced as more data are used for selection, leaving lesser information for inference.
3. Randomized hierarchical screening to identify interesting eQTL effects
Our data will include measurements on the expression levels of 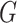 genes and
genes and 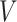 variants in
variants in 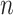 subjects. We denote the outcome variables using
subjects. We denote the outcome variables using 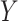 :
: 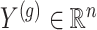 is the vector of gene-expression levels for gene
is the vector of gene-expression levels for gene 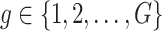 . Let
. Let 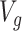 be the number of variants measured within a defined cis window around gene
be the number of variants measured within a defined cis window around gene 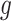 : we indicate the matrix of the corresponding potential explanatory variables with
: we indicate the matrix of the corresponding potential explanatory variables with 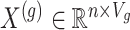 . We assume, without loss of generality, that
. We assume, without loss of generality, that 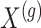 is centered and the columns are scaled to have norm
is centered and the columns are scaled to have norm 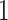 . Denote the variance in gene-expression response
. Denote the variance in gene-expression response 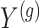 by
by 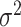 . In this section, we are going to outline a randomized selection procedure that mimics the hierarchical strategy often adopted in the literature (Lonsdale and others, 2013) and specify the derived “target of inference.”
. In this section, we are going to outline a randomized selection procedure that mimics the hierarchical strategy often adopted in the literature (Lonsdale and others, 2013) and specify the derived “target of inference.”
3.1. A hierarchical randomized selection
Following the practice in eQTL studies, we want to first identify a set 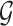 of genes that appear likely to be cis regulated, and then, for each of the genes
of genes that appear likely to be cis regulated, and then, for each of the genes 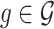 identify a set of potential e-variants
identify a set of potential e-variants 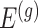 belonging to the cis region and appearing to have an effect on the expression of gene
belonging to the cis region and appearing to have an effect on the expression of gene 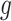 . In order to both use the entire sample
. In order to both use the entire sample 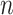 to guide our selection and, at the same time, reserve enough information for the following inference on the effect size, we explore the potential of a selection strategy that includes randomization in both these stages. The “cartoon” examples with which we concluded the previous section illustrate the advantages of randomization. For a more comprehensive discussion, please see Tian and others (2018) and Dwork and others (2015), which place this into the context of data re-use.
to guide our selection and, at the same time, reserve enough information for the following inference on the effect size, we explore the potential of a selection strategy that includes randomization in both these stages. The “cartoon” examples with which we concluded the previous section illustrate the advantages of randomization. For a more comprehensive discussion, please see Tian and others (2018) and Dwork and others (2015), which place this into the context of data re-use.
Stage-I: Randomized selection of eGenes To discover promising genes, we test the global nulls that the expression of gene 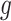 is not influenced by any of the cis variants
is not influenced by any of the cis variants 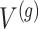 :
: 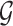 collects the set of genes for which we reject this null controlling FDR at level q. The p-values for these global null hypotheses are calculated with randomization.
collects the set of genes for which we reject this null controlling FDR at level q. The p-values for these global null hypotheses are calculated with randomization.
Step 1. Compute for each gene 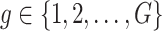 , a univariate t-test statistic based on marginal correlation of local variant
, a univariate t-test statistic based on marginal correlation of local variant 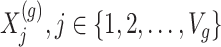 with gene expression
with gene expression 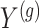 and added Gaussian randomization
and added Gaussian randomization 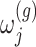 . The perturbed t-statistic (z-statistic for a known
. The perturbed t-statistic (z-statistic for a known 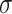 ) is given by
) is given by
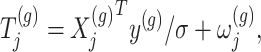 |
(3.1) |
where 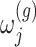 is a realization of a Gaussian random variable
is a realization of a Gaussian random variable 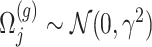 with
with 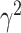 controlling the amount of perturbation. Further, perturbations
controlling the amount of perturbation. Further, perturbations 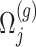 are independent for
are independent for 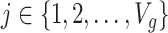 and also, independent across all genes
and also, independent across all genes 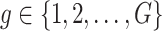 . For settings where
. For settings where 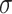 is unknown, we use a marginal estimate of
is unknown, we use a marginal estimate of 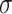 ; see Remark 3.2.
; see Remark 3.2.
Step 2. Compute a global p-value based on Bonferroni 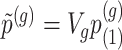 , where
, where
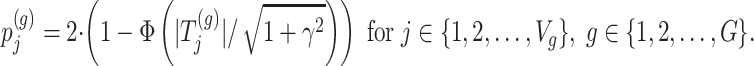 |
Step 3. We apply a Benjamini–Hochberg (BH-q) procedure at level 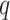 to the global p-values
to the global p-values 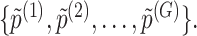 Based on the rejection set of BH, we report
Based on the rejection set of BH, we report 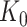 eGenes with the number of rejections calculated as
eGenes with the number of rejections calculated as 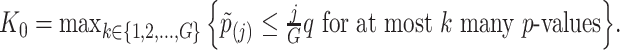 This set of identified genes is denoted as
This set of identified genes is denoted as 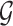 . The analogous non-randomized selection procedure is based on t-statistics in (3.1) with no added perturbation.
. The analogous non-randomized selection procedure is based on t-statistics in (3.1) with no added perturbation.
Stage-II: Randomized selection of potential eVariants The second stage identifies promising variants 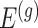 for each of the eGenes
for each of the eGenes 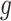 in
in 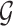 . We use a randomized version of penalized regression (Zou and Hastie, 2005), where the
. We use a randomized version of penalized regression (Zou and Hastie, 2005), where the 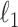 penalty induces sparsity (selection) and a small
penalty induces sparsity (selection) and a small 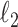 penalty is used to regularize the problem. The set
penalty is used to regularize the problem. The set 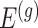 is identified by solving:
is identified by solving:
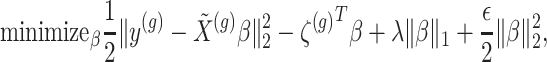 |
(3.2) |
where 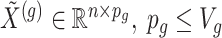 indicate a pruned set of cis variants. The value of
indicate a pruned set of cis variants. The value of 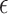 is small, with the only goal of ensuring the existence of a well-defined solution, while
is small, with the only goal of ensuring the existence of a well-defined solution, while 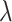 is set to be the theoretical value considered in Section 2. In the same spirit as the randomized screening of eGenes,
is set to be the theoretical value considered in Section 2. In the same spirit as the randomized screening of eGenes, 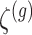 is based on a Gaussian variable
is based on a Gaussian variable 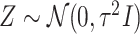 .
.
Note that 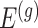 indicates the set of active variants for the problem (3.2) for gene
indicates the set of active variants for the problem (3.2) for gene 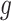 : this is the result of our selection step. However, the final results of our analysis will consist of a set
: this is the result of our selection step. However, the final results of our analysis will consist of a set 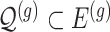 , corresponding to the subset of variants with significant selection-adjusted p-values at a chosen level of selective Type-I control
, corresponding to the subset of variants with significant selection-adjusted p-values at a chosen level of selective Type-I control 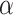 .
.
Remark 3.1
We noted that problem (3.2) is defined on pruned set of variants. The variants in the cis region of a gene can be highly correlated in the sample. This makes it hard for any multi-regression analysis like the LASSO to recover the set of variables truly associated and hence, pruning becomes essential; prior works Hastie and others (2000) and Reid and Tibshirani (2016) have recognized these challenges. We give details of an unsupervised pruning of variants using a hierarchical clustering scheme, based on the empirical correlations between variants as a distance measure in Section A of supplementary material available at Biostatistics online.
Remark 3.2
In real data analysis, the variance of gene expressions is not known: we use a plug-in estimate and refer to Tian and others (2018) that justifies this choice through a consistency result. For the marginal screening step, we consider a marginal estimate of variance to compute a t-statistic for the association between variant
and outcome. For the randomized LASSO screening, we use an estimate of
from a refitted least squared regression post the LASSO.
Remark 3.3
The variation of perturbation controls the amount of randomization in the selection pipeline and determines the tradeoff between selection quality and inferential performance. We choose the perturbation-to-noise ratio
,
being an estimate of the noise level, in both stages of eGene and eVariant selections. To see that this is a reasonable choice for the perturbation variance, we point our readers to the GTEx Liver data analysis in Section 5.2, where we select
of the eGenes and subsequently,
of the eVariants for these eGenes discovered by (a closely replicated version of) the GTEx pipeline (Lonsdale and others, 2013). Further, at this scale of randomization variance, we observe a significant reduction of average lengths of the “Proposed” intervals by
in comparison to non-randomized selective inference by Lee and others (2016)—thus achieving high inferential power at a satisfactory selection performance.
3.2. Model and adaptive target
To proceed with inference post a hierarchical screening, we assume a full Gaussian model for gene expression, as in the motivating examples:
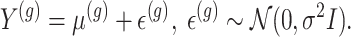 |
(3.3) |
The generative law in this framework parameterizes the Gaussian mean as 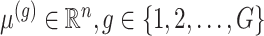 . In addition, we assume that errors
. In addition, we assume that errors 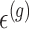 are independent across genes.
are independent across genes.
Remark 3.4
Gene-expression measurements and genotype data often are affected by confounding factors, including gender, demography, platform etc. For the purposes of this article, we assume that the data have undergone preprocessing that eliminates the effects of hidden confounding factors and measured covariates. This allows us to assume that the noise is approximately independent across genes. Details on how these confounding factors are regressed out from the real data we analyze is provided in Section C of supplementary material available at Biostatistics online.
Having described a model, we define the adaptive target of inference as the projection of the model parameters onto the space spanned by 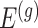 for each gene
for each gene 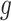 :
:
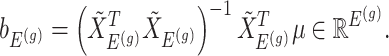 |
(3.4) |
Denoting the 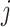 th component of the adaptive partial regression coefficient
th component of the adaptive partial regression coefficient 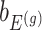 as
as 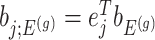 , we note that unadjusted inference for
, we note that unadjusted inference for 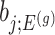 would be based on the
would be based on the 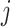 th least squared estimator:
th least squared estimator: 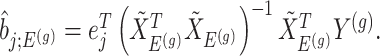 Under an independent Gaussian noise model,
Under an independent Gaussian noise model, 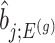 is the MLE for
is the MLE for 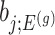 and naive confidence intervals for the same target are centered around
and naive confidence intervals for the same target are centered around 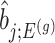 with a length of
with a length of 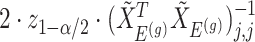 ;
; 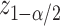 being the standard normal quantile. In the next section, we will describe alternative point and interval estimates for these quantities that take into account the selection we have described.
being the standard normal quantile. In the next section, we will describe alternative point and interval estimates for these quantities that take into account the selection we have described.
4. Selection-adjusted inference for eVariants effects
We outline a recipe to provide selection-adjusted inference for the adaptive partial regression coefficients in (3.4) in a coordinate-wise manner. That is, we provide the steps to get a tractable selection-adjusted law: 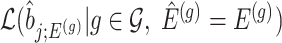 , the conditional law of the
, the conditional law of the 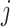 th component of the least squared estimator conditioned upon the event that gene
th component of the least squared estimator conditioned upon the event that gene 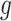 was screened marginally in Stage-I and
was screened marginally in Stage-I and 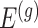 was screened by randomized LASSO in Stage-II. We start again by listing the notation and terminology we will use. Then, we give an outline of the steps that provide a practical selection adjustment for inference.
was screened by randomized LASSO in Stage-II. We start again by listing the notation and terminology we will use. Then, we give an outline of the steps that provide a practical selection adjustment for inference.
Data and randomization At the core of the adjustment for selection is the calculation of a conditional likelihood. Because of the randomization we introduced, the relevant likelihood includes both the original data and the outcome of the randomization. The observed data
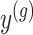 and randomizations
and randomizations 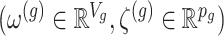 are realizations of the random variables
are realizations of the random variables 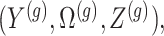 respectively;
respectively; 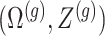 represent the random variables for Gaussian randomizations used in both stages of selection. The entire data across all genes are denoted by
represent the random variables for Gaussian randomizations used in both stages of selection. The entire data across all genes are denoted by 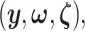 where
where 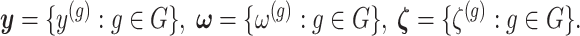
Parameters in model In providing coordinate-wise inference, we note that the target parameter in our case is
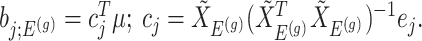 Based on (3.3), there are nuisance parameters that are given by
Based on (3.3), there are nuisance parameters that are given by 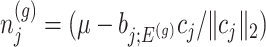 . In a nutshell,
. In a nutshell, 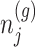 are parameters that we are not interested in inferring about while providing inference for
are parameters that we are not interested in inferring about while providing inference for 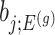 .
.Target and null statistic A target statistic is a statistic that can be used to make inference on the target parameter
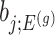 . Specifically, we will consider the
. Specifically, we will consider the 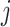 th coordinate of the least squared estimator, denoted by
th coordinate of the least squared estimator, denoted by 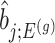 as the target statistic for target parameter—
as the target statistic for target parameter—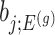 . Note that
. Note that 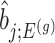 also, serves as the target statistic for naive (unadjusted) inference for
also, serves as the target statistic for naive (unadjusted) inference for 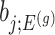 . Except now, the law of this target statistic is no longer a Gaussian distribution centered around
. Except now, the law of this target statistic is no longer a Gaussian distribution centered around 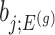 : the goal of the remaining section is to provide a tractable selection-adjusted law for
: the goal of the remaining section is to provide a tractable selection-adjusted law for 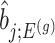 . The null statistic according to model (3.3) is a data vector that is orthogonal to
. The null statistic according to model (3.3) is a data vector that is orthogonal to 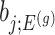 based on decomposition
based on decomposition 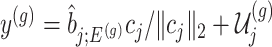 . In model (3.3), the mean of the null statistic is the nuisance parameter, defined as
. In model (3.3), the mean of the null statistic is the nuisance parameter, defined as 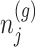 . Conditioning out the null statistics in the selection-adjusted law eliminates the nuisance parameters in the model.
. Conditioning out the null statistics in the selection-adjusted law eliminates the nuisance parameters in the model.Variance of target and null statistic Finally, denote as
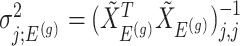 , the variance of
, the variance of 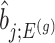 and the variance of
and the variance of 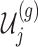 as
as 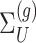 under (3.3).
under (3.3).
4.1. An outline of conditional inference after randomized selection in eQTL
In order to successfully apply conditional inference, we need to be able to efficiently compute with the selection-adjusted law. To achieve this goal in the eQTL inference problem that we have described, we take the following steps.
I. A selection-adjusted law across the genome The randomized selection 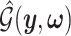 of eGenes and of promising variants for each eGene
of eGenes and of promising variants for each eGene 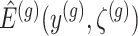 define a selection event
define a selection event 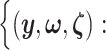
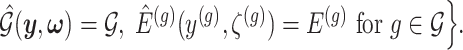 Conditioning on this event modifies the law of data and randomizations:
Conditioning on this event modifies the law of data and randomizations: 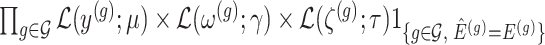 , where
, where 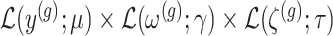 is the unadjusted law of
is the unadjusted law of 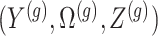 .
.
The above conditional law results from the fact that we infer about target (3.4) for a gene  only if it has been screened in the set of eGenes and the set
only if it has been screened in the set of eGenes and the set  of variants are chosen by a randomized version of LASSO. We point out to our readers that the selection of gene
of variants are chosen by a randomized version of LASSO. We point out to our readers that the selection of gene 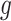 as an eGene depends not only on the data specific to gene
as an eGene depends not only on the data specific to gene 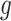 , but also on data for all other genes. This leads to a complicated selection event, which simplifies to a great extent when we condition additionally on some more information beyond knowing the set of eGenes:
, but also on data for all other genes. This leads to a complicated selection event, which simplifies to a great extent when we condition additionally on some more information beyond knowing the set of eGenes: 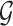 and the respective active variants
and the respective active variants 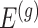 , chosen in the next stage. This extra information includes signs of t-statistics for the selected genes, the signs of Lasso coefficients, the total number of eGenes
, chosen in the next stage. This extra information includes signs of t-statistics for the selected genes, the signs of Lasso coefficients, the total number of eGenes 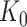 , etc.
, etc.
II. A simplified adjusted law across eGenes We obtain a simplified selection event 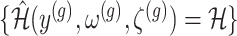 by conditioning on some additional information together with the selection of eGene
by conditioning on some additional information together with the selection of eGene 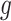 and variants
and variants 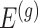 selected by LASSO. Such an event is easier to handle in the sense that it is described only in terms of data specific to gene
selected by LASSO. Such an event is easier to handle in the sense that it is described only in terms of data specific to gene 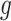 and thereby, allows a decoupling of the joint law above into an adjusted law for each gene in
and thereby, allows a decoupling of the joint law above into an adjusted law for each gene in 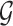 . A full description of the conditioning event, a superset of the event
. A full description of the conditioning event, a superset of the event 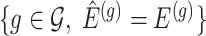 is available in Section B.1 of supplementary material available at Biostatistics online.
is available in Section B.1 of supplementary material available at Biostatistics online.
Under (3.3) and Gaussian randomizations, the simplified selection-adjusted density for each eGene 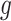 in terms of target and null statistic
in terms of target and null statistic 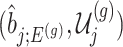 , randomizations
, randomizations 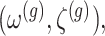 and an observed selection
and an observed selection 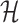 , is given by
, is given by
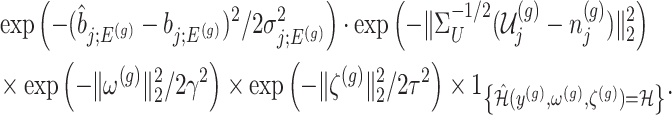 |
(4.5) |
III. Selection-adjusted interval and point estimates Since, we are interested in the selection-adjusted law of the target statistic 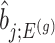 , we marginalize over the randomizations in the joint law in (4.5) and condition on nuisance statistics
, we marginalize over the randomizations in the joint law in (4.5) and condition on nuisance statistics 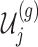 in order to eliminate nuisance parameters
in order to eliminate nuisance parameters 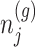 . This finally, leads to a selection-adjusted density for the target statistic
. This finally, leads to a selection-adjusted density for the target statistic 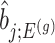 , proportional to
, proportional to
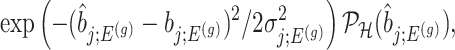 |
(4.6) |
where 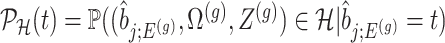 is the conditional probability of selection given
is the conditional probability of selection given 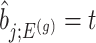 . This is the adjusted density to carry out inference on the effect sizes of eVariants.
. This is the adjusted density to carry out inference on the effect sizes of eVariants.
Using the corrected law of the target statistic to define 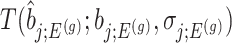 that equals
that equals
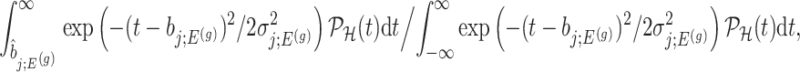 |
an adjusted (two-sided) p-value can be computed as:
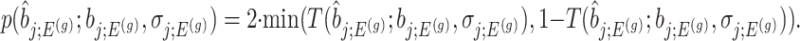 |
Confidence intervals for 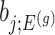 with target coverage
with target coverage 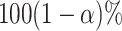 are constructed as
are constructed as
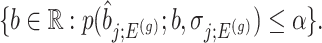 |
(4.7) |
And, a MLE is obtained solving
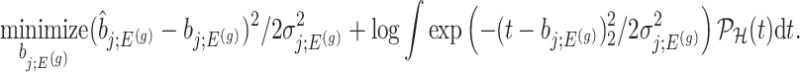 |
(4.8) |
IV. Approximate and tractable inference Even though, we derived a selection-adjusted law in (4.6), the term 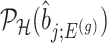 , the conditional selection probability in (4.6), lacks a tractable closed form expression. This contributes to the computational bottleneck in constructing intervals or solving a MLE problem based on the adjusted law of
, the conditional selection probability in (4.6), lacks a tractable closed form expression. This contributes to the computational bottleneck in constructing intervals or solving a MLE problem based on the adjusted law of 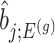 . For a single selection query cast on the data, an approximation for the adjusted law is proposed in Panigrahi and others (2017). To offer tractable inference based on (4.6), we provide an approximation for
. For a single selection query cast on the data, an approximation for the adjusted law is proposed in Panigrahi and others (2017). To offer tractable inference based on (4.6), we provide an approximation for 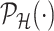 . Details on the approximation are given in Section B.2 of supplementary material available at Biostatistics online. Approximate inference in the form of interval and point estimates is based on plugging
. Details on the approximation are given in Section B.2 of supplementary material available at Biostatistics online. Approximate inference in the form of interval and point estimates is based on plugging 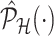 in (4.7) and (4.8). We make precise the steps involved in obtaining the simplified conditional law (II) and the approximation of the marginal adjusted law (IV) in Section B of supplementary material available at Biostatistics online.
in (4.7) and (4.8). We make precise the steps involved in obtaining the simplified conditional law (II) and the approximation of the marginal adjusted law (IV) in Section B of supplementary material available at Biostatistics online.
5. Performance in a cis-eQTL study
In this section and the next, we examine the properties of the proposed pipeline by testing its performance on data collected in one eQTL study (Lonsdale and others, 2013) and comparing its results with those of two other “benchmark” procedures. We first rely on simulations of the outcome variables according to a known model based on genotype data in order to evaluate a number of performance metrics and then turn to the analysis of the real data. The dataset we analyze is the collection of liver samples in V6p of the GTEx study (Lonsdale and others, 2013). It comprises 97 individuals, with genotypes for 7 207 740 variants (these variants are obtained as the output of the default imputation pipeline implemented in Lonsdale and others (2013)) and expression quantification for 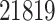 genes. Details on data acquisition and preprocessing are provided in the Section C of supplementary material available at Biostatistics online.
genes. Details on data acquisition and preprocessing are provided in the Section C of supplementary material available at Biostatistics online.
In studying the performance of the proposed pipeline, we compare it with (i) a slightly modified version of the analysis strategy in the original GTEx paper, followed by a naive construction of the confidence interval for the effect sizes of the identified eVariant (GTEx+vanilla); (ii) a strategy that uses “out-of-the-box” selective inference tools and employs no randomization during the selection steps (Bonf+Lasso+Lee et al.). Specifically,
GTEx+vanilla (G.V.) The selection of eGenes is done controlling FDR at level 0.1 with the BH procedure applied to p-values for the global null obtained via the Simes’ combination rule Simes (1986). We note that this differs from the original GTEx paper in two minor ways: the p-values for the global null for eGene discoveries are obtained via Simes rather than permutations in Lonsdale and others (2013), and the adopted FDR controlling procedure at this stage is BH rather than Storey’s procedure referred in the GTEx paper. In the second stage, the eVariants are selected by an adaptive forward–backward selection: a variable is added to the regression only if it p-value is lower than the largest p-value for global nulls in the set of discovered eGenes [with details given in Lonsdale and others (2013)]. To estimate effect size, we fit the least squared estimator on the selected model for the point estimate and use the normal quantiles to construct intervals, thereby “naively” ignoring the selection in the two screening stages.
Bonf+Lasso+Lee et al. (B.L.L.) The screening is conducted in a two-stage procedure similar to our proposed pipeline, with the exception that there is no randomization in the t-statistics or in the second stage selection of eVariants. The confidence intervals for effect sizes are constructed using the adjustments for the LASSO detailed in Lee and others (2016). We note that this approach only accounts for the eVariant selection the second stage, but not for eGene selection in the first stage. Further, Lee and others (2016) does not give a selection-adjusted point estimate, so we report the unadjusted least squared estimator on the selected variants as a point-estimate.
Comparing our proposed procedure with these two alternatives, therefore, enables us to study how its performance relates to that of (i) a state-of-the-art method for the identification of eVariants that does not take into account at all the effect of selection at the inferential stage, and to that of (2) an approach to correct for selection that relies on out-of-the-box tools, without fully capturing the hierarchical identification of eVariants and not capitalizing on the possible power increases due to randomization.
5.1. Simulation study
We start with a simulation study to explore the performance of the different procedures: using the genotypes from the GTEx liver sample, we generate artificial gene-expression values and investigate how the three approaches reconstruct the effect sizes of eVariants.
5.1.1. Data generation
In choosing a strategy to simulate gene-expression values, we followed the following principles: (i) the selection strategy in G.V. should lead to a number of eGene and eVariant discoveries similar to those detected in the real data in Lonsdale and others (2013); (ii) there should be some genes that are not true eGenes, so that it is sensible to consider “false discoveries”; (iii) there should be eGenes regulated by multiple eVariants; and (iv) the model should be as simple as possible, to make the interpretation of the results straightforward. After experimenting with a few models, that satisfied criteria (ii)–(iv), we found the following to be the one that gave results closer to those in Lonsdale and others (2013) and adopted it. For each gene 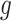 for which gene expression is available in the real data, and for which
for which gene expression is available in the real data, and for which 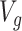 cis variants have been genotyped, we generate a vector
cis variants have been genotyped, we generate a vector 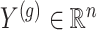 of synthetic gene expression as follows.
of synthetic gene expression as follows.
i. We randomly set the number of causal variants
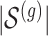 from
from 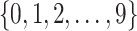 according to the distribution in Figure 2 of supplementary material available at Biostatistics online, so that approximately a third of genes contain at least one true signal.
according to the distribution in Figure 2 of supplementary material available at Biostatistics online, so that approximately a third of genes contain at least one true signal.ii. A set
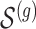 of causal variants of the selected size is drown randomly from the variants in the cis region. To assure, however, that the desired number of “independent” signals is present, we want to make sure that
of causal variants of the selected size is drown randomly from the variants in the cis region. To assure, however, that the desired number of “independent” signals is present, we want to make sure that 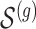 does not contain variants that are closely correlated and whose contribution to the gene-expression value would be indistinguishable. To achieve this goal, we subject the genotyped variants to hierarchical clustering with minimax linkage (an unsupervised pruning technique detailed in Section A of supplementary material available at Biostatistics online): we randomly select
does not contain variants that are closely correlated and whose contribution to the gene-expression value would be indistinguishable. To achieve this goal, we subject the genotyped variants to hierarchical clustering with minimax linkage (an unsupervised pruning technique detailed in Section A of supplementary material available at Biostatistics online): we randomly select 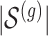 clusters, and randomly assign an element in the cluster to be a causal variant. We also rely on this same clustering to identify a “pruned” set of variants that will constitute the input of the penalized regression, which needs to work on non-collinear variables. From each of these clusters, we choose a representative, correlated by at least
clusters, and randomly assign an element in the cluster to be a causal variant. We also rely on this same clustering to identify a “pruned” set of variants that will constitute the input of the penalized regression, which needs to work on non-collinear variables. From each of these clusters, we choose a representative, correlated by at least 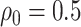 with all members of that cluster. We remark that the cluster representative and the possible causal variant residing in the cluster do not necessarily coincide.
with all members of that cluster. We remark that the cluster representative and the possible causal variant residing in the cluster do not necessarily coincide.iii. The expression values
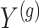 are generated according to the following model
are generated according to the following model 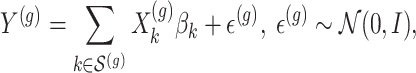 where the noise vector
where the noise vector 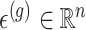 is independently sampled for each gene, each
is independently sampled for each gene, each 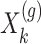 is standardized with mean zero and unit variance, and true effect sizes are
is standardized with mean zero and unit variance, and true effect sizes are 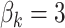 .
.
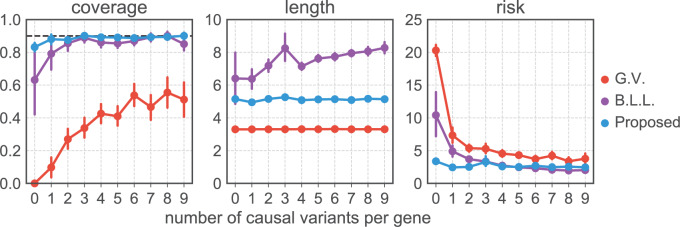
Fig. 2.
Comparison of coverages (a) and lengths (b) of confidence intervals and risk (c) of the MLE for the adaptive targets resulting from three different methods: GTEx+vanilla (G.V., red), Bonf+Lasso+Lee et al. (B.L.L., purple), and our proposed pipeline (blue). The values are averaged across all the selected genes with the same true number of causal variants, reported on the 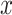 -axis. The target coverage is 0.9, corresponding to the dotted horizontal line in the first panel. The dots represent the averages across all eGenes within a signal regime, and the vertical bars represent one standard deviation in both directions.
-axis. The target coverage is 0.9, corresponding to the dotted horizontal line in the first panel. The dots represent the averages across all eGenes within a signal regime, and the vertical bars represent one standard deviation in both directions.
5.1.2. Evaluation metrics
Because of the computational costs associated to the analysis methods, we do not repeat the data generating process multiple times for a given gene, rather we interpret our results by aggregating across genes with the same number of causal variants. The focus of this work is to provide methods that allow correct inference for the adaptive target defined in (3.4), dependent on the selection of variants associated with each eGene. To evaluate the performance of the three approaches with this respects, we rely on three quantities: the coverage of the confidence intervals, their lengths, and the average empirical risk of the point estimate computed with respect to a quadratic loss function. Note that the parameters to be estimated in the loss metric for risk evaluation are the adaptive targets.
At the same time, given that the three procedures differ in their selection steps, to interpret appropriately the results, it is useful to also compare them at the level of selection. In keeping with the hierarchical structure of the selection, there are two levels at which it makes sense to talk about FDR and power: the eGene level and the eVariant level, for selected eGenes. FDR and power are easily defined for eGenes. To explore the performance at the level of eVariants, we are going to focus on the eVariants for selected eGenes (therefore, eVariants for erroneously missed eGenes are not going to be considered in our power evaluation). Our proposed pipeline and B.L.L. receive as input only cluster representative SNPs and therefore can only identify these as eVariants: we consider their discoveries correct if they correspond to a cluster that contains a true causal variants; likewise we consider a causal variant discovered if the cluster that contains it has been selected. We further note that the selection-adjusted confidence intervals can be used to refine the selection of eVariants: while regularized regression might estimate a coefficient as different from zero, if the corresponding adjusted confidence interval covers zero, it make sense to discard the eVariant from the discovery set. Therefore, it seems appropriate to evaluate FDR and power on the basis of this final post-inference set.
5.1.3. Results and insights
Figures 2 and 3 summarize the results of the simulations, the first focusing on the inference on effect sizes, which is the object of the present article, and the second anchoring these results in the context of FDR and Power. Figure 2 clearly illustrates that our pipeline succeeds in producing confidence intervals with the correct empirical coverages, and that the lengths of these confidence intervals are not unduly large. The failure of G.V. to produce confidence intervals with the right coverage is expected: the interest of our results is in showing the extent of the departure. While adjusting for eVariant selection as in B.L.L. improves coverage, the approach still falls short of the target for variances in erroneously selected eGenes and for eGenes with a small number of causal variants. Moreover, the lengths of these adjusted confidence intervals are substantially longer than the ones we propose, which are just 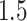 times longer than the naive—this is the advantage of randomization.
times longer than the naive—this is the advantage of randomization.
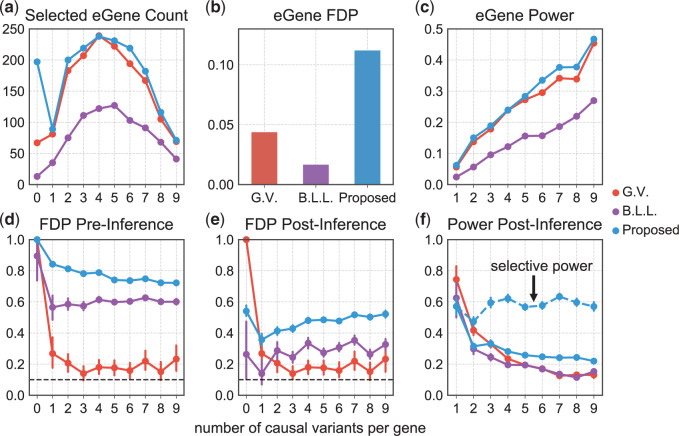
Fig. 3.
Summary of FDR (at level 0.1) and power for eGene and eVariants. The top row refers to eGenes and reports (a) the total number of discovered eGenes, (b) the FDR, and (c) power. The bottom row, (d), (e), and (f) refers to eVariants and focuses only on the eVariants relative to the discovered eGenes for each method. (d) It calculates FDR for each of the gene categories on the basis of the results of the selection procedures; (e) it shows how these results change once parameters whose adjusted confidence intervals cover zero are eliminated; and (f) it illustrates the power corresponding to the selection in (e). (a), (c), (d), (e), and (f) These are tabulated for each of the ten categories of genes, defined by their true number of causal variants.
Figure 3 puts these results in context of the selection outputs of the three different methods. Looking at eGene selections, we can see that B.L.L. is unduly conservative at the eGene level as its FDR is much lower than that of our procedure. It is reassuring to note that Proposed has slightly higher power than the benchmark G.V. at the eGene selection level, while controlling for FDR at the level of 0.1. At the eVariant selection stage, we report the FDR of the screening procedure standard (used in B.L.L.) and randomized regularized regression (used in Proposed) and the forward–backward selection (used in G.V.). The average number of eVariants per eGenes reported by the methods are shown in Table 1 of supplementary material available at Biostatistics online. Because the number of declared eVariants (post-inference) are determined by whether their intervals cover 0 or not among the screened evariants (pre-inference) for both B.L.L. and Proposed, we see the decrease in the average number of reported variants with the exception of forward–backward selection. In G.V., the eVariants (reported variants) are selected by an adaptive forward–backward selection and this report is not impacted by inference; thereby, the false discovery proportion (FDP) curve is the same both pre- and post-inference for G.V. Both the standard and randomized regularized regression do not appear to control the FDR (Figure 3(d)): correction based on the adjusted confidence intervals (see Figure 3(e)) reduces false discoveries from (d) by about 20–45%. Note that the FDR level with the proposal is significantly better for genes that have 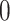 signals, but declared as eGenes, which G.V. does not redeem for at all in the second stage of screening. The performance at eGenes, however still is inferior to the one of G.V. It is rather reassuring that the selections of G.V., which practically coincide with those reported in Lonsdale and others (2013), have low FDR at eGenes: this documents the efforts of a large community of scientists whose focus was precisely the selection of eVariants. The overall worse FDR control with the proposed pipeline is ascribable to the property of the selection procedure itself, in this case the LASSO which does not have screening guarantees in terms of FDR. Still, evident from Figure 3(e), our results are encouraging as the inference step contributes to decreasing the FDP considerably, mitigating the worse performance of the selection step to some extent. See an example in Section D of supplementary material available at Biostatistics online on the discrepancy between FDR control and selective false coverage rate control.
signals, but declared as eGenes, which G.V. does not redeem for at all in the second stage of screening. The performance at eGenes, however still is inferior to the one of G.V. It is rather reassuring that the selections of G.V., which practically coincide with those reported in Lonsdale and others (2013), have low FDR at eGenes: this documents the efforts of a large community of scientists whose focus was precisely the selection of eVariants. The overall worse FDR control with the proposed pipeline is ascribable to the property of the selection procedure itself, in this case the LASSO which does not have screening guarantees in terms of FDR. Still, evident from Figure 3(e), our results are encouraging as the inference step contributes to decreasing the FDP considerably, mitigating the worse performance of the selection step to some extent. See an example in Section D of supplementary material available at Biostatistics online on the discrepancy between FDR control and selective false coverage rate control.
Table 1.
Comparison of total number of reported eVariants between two methods
| Across common eGenes | Across all eGenes | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Proposed | Proposed | |||||||||
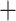
|

|
Total |
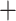
|

|
Total | |||||
| GTEx benchmark |
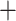
|
1224 | 439 | 1663 | GTEx benchmark |
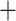
|
1224 | 837 | 2061 | |

|
4584 |

|
8175 | |||||||
| Total | 5808 | Total | 9399 | |||||||
To highlight the power associated exclusively with the randomized conditional strategy to inference, we include a power metric for the proposed approach that computes the proportion of true signals discovered divided by the number of true signals screened. The broken line in Panel (f) depicts the conditional power, recording as high as 60–65% success rate of detecting a signal post our proposed inference, conditional on the signal being screened by the selection procedure. Thus, adopting selection strategies that mimic more closely the eVariant screening in the second stage in GTEx will lead to improved and comparable FDR metrics while deploying our inferential pipeline post such a selection will provide reliable effect size estimates for the identified eVariants with a promisingly high power of detection.
We conclude this analysis section by providing the link to the code developed for our methods in a simulation prototype at https://github.com/snigdhagit/selective-inference/tree/simulation_prototype/selection/simulation_prototype. Details of the simulation setting and the coding pipeline are provided in Section E of supplementary material available at Biostatistics online.
5.2. Effect sizes in GTEx liver data
We now turn to the analysis of the real expression data available for liver in Lonsdale and others (2013). We analyze the data using the three procedures we compared via simulation, reporting the eVariants whose adjusted-interval estimates does not cover 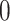 .
.
Our pipeline identified 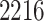 eGenes, with
eGenes, with 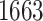 in common with the G.V., which detects
in common with the G.V., which detects 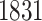 eGenes in all. The B.L.L. selects
eGenes in all. The B.L.L. selects 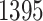 eGenes,
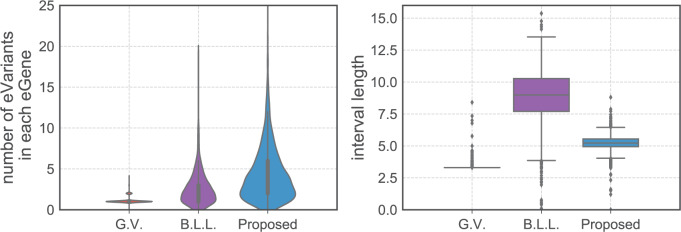
eGenes, 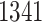 of which are also identified by our proposal. Figure 4 illustrates the eVariants results: the number of detected eVariants and distribution of the lengths of their confidence intervals. The pipeline we have constructed detects an average of
of which are also identified by our proposal. Figure 4 illustrates the eVariants results: the number of detected eVariants and distribution of the lengths of their confidence intervals. The pipeline we have constructed detects an average of 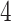 –
–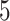 eVariants per gene, while B.L.L. reports
eVariants per gene, while B.L.L. reports 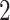 –
–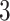 eVariants on an average and G.V.
eVariants on an average and G.V.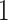 eVariant on average per eGene. Our simulations indicate that both our proposed procedure and B.L.L. tend to have higher FDR than G.V., so that we cannot assume all the additional discoveries to be valid ones. Nevertheless, even assuming a false discovery rate as high as 50%, the number of extra discoveries is such that we can expect that B.L.L. and our proposed method do allow the identification of a considerable number of additional true discoveries, or, in other words, that G.V underestimates the number of eVariants. In fact, this is corroborated by Table 1 that compares the total number of eVariant findings between G.V. and the proposed pipeline. The table in the left panel gives the number of common and exclusive eVariants reported by each procedure across the common eGenes; a total of
eVariant on average per eGene. Our simulations indicate that both our proposed procedure and B.L.L. tend to have higher FDR than G.V., so that we cannot assume all the additional discoveries to be valid ones. Nevertheless, even assuming a false discovery rate as high as 50%, the number of extra discoveries is such that we can expect that B.L.L. and our proposed method do allow the identification of a considerable number of additional true discoveries, or, in other words, that G.V underestimates the number of eVariants. In fact, this is corroborated by Table 1 that compares the total number of eVariant findings between G.V. and the proposed pipeline. The table in the left panel gives the number of common and exclusive eVariants reported by each procedure across the common eGenes; a total of 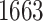 eGenes are reported by both. The table in the right panel compares the eVariant findings across all eGenes reported by any of these proposals.
eGenes are reported by both. The table in the right panel compares the eVariant findings across all eGenes reported by any of these proposals.
Fig. 4.
Left panel gives the distribution of the number of eVariants per eGene as reported by the three methods of inference. Right panel plots average lengths of intervals using the interval estimates based on the same.
6. Discussion
In many genomic studies, the first step of data analysis identifies interesting associations between variables. Inference of parameters governing these associations is attempted only in a second stage. Naive estimates, that rely on standard methods using the same data that suggested importance of these associations, do not enjoy reliable statistical properties. When the studies, however, rely on scarce biological samples, data-splitting (or deferring to a new sample for inference) is not a viable option. The studies of genetic regulation of gene expression in hard-to-access human tissues are a perfect exemplification of these challenges. In this work, we have explored the extent to which the conceptual framework of conditional inference after selection can be brought to provide researchers with reliable tools to estimate the effect size associated to DNA variants, associated with variation in gene expression. Following the standard practice in the eQTL community, we have described a two-stage process for the selection of relevant cis variants: first genes under cis regulations are identified, and then the subset of important variants in their vicinity.
Deriving appropriate conditional inference in this setting presented a number of challenges. In addition to accounting for a two-staged selection process, calculation of interval and point estimates is more involved post-randomization unlike the easy computation of intervals based on a truncated Gaussian law in Lee and others (2016). To bypass the fact that the exact selection-adjusted law lacks a closed form expression, we introduce an approximation strategy that is likely to be useful in other contexts. A simulation study on the scale of real data underscored the dangers of ignoring selection at the inferential stage: naive confidence intervals for effect sizes of variants identified with a published strategy missed the target coverage by a wide margin. The offered pipeline leads to confidence intervals with correct coverage and lengths, appreciably shorter than those obtained with out-of-the-box tools for conditional inference. While these results are encouraging, we also noted that the selection procedure in our pipeline has appreciably worse performance that state-of-the-art variant selection strategies in terms of FDR. Specifically, we observe that the regularized regression we adopted does not enjoy FDR control. In fact, we realize that the techniques in this work are amenable to a more general framework of convex learning programs, with the proposed mining pipeline as a specific example in this broader class of selection schemes. This paves way for interesting future directions to study if computation for conditional inference can be carried out for other selection strategies with better FDR control, as SLOPE, the knockoffs, etc. We conclude with the hope to take on these challenges in other biological contexts with this work as a first attempt of tractably addressing the issue of selection bias in effect size estimation in eQTL.
Supplementary Material
Acknowledgments
The authors acknowledge that data for the gene-expression analysis was acquired using dbGaP accession number phs000424.v6.p1. S.P. would like to thank Jonathan Taylor for several helpful discussions regarding this project. The authors thank the anonymous reviewers for their helpful comments that have led to improvements in the draft.
Conflict of Interest: None declared.
Funding
Stanford Graduate Fellowship to J.Z.; NSF DMS (1712800 J.Z. to C.S.); and NIH (R01MH101782 to C.S.).
References
- Benjamini, Y. and Hochberg, Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society: Series B (Methodological) 57, 289–300. [Google Scholar]
- Berk, R.,, Brown, L.,, Buja, A.,, Zhang, K.,, Zhao, L. (2013). Valid post-selection inference. The Annals of Statistics 41, 802–837. [Google Scholar]
- Dwork, C., Feldman, V., Hardt, M., Pitassi, T., Reingold, O. and Roth, A. L. (2015). Preserving statistical validity in adaptive data analysis. In: Proceedings of the Forty-Seventh Annual ACM Symposium on Theory of Computing. ACM, pp. 117–126. [Google Scholar]
- Lonsdale, J.,, Thomas, J.,, Salvatore, M.,, Phillips, R.,, Lo, E.,, Shad, S.,, Hasz, R.,, Walters, G.,, Garcia, F.,, Young, N. and others (2013). The genotype-tissue expression (GTEx) project. Nature Genetics 45, 580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastie, T., Tibshirani, R., Eisen, M. B., Alizadeh, A., Levy, R., Staudt, L., Chan, W. C., Botstein, D. and Brown, P. (2000). ‘Gene shaving’ as a method for identifying distinct sets of genes with similar expression patterns. Genome Biology 1, research0003–1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee, J. D., Sun, D. L., Sun, Y. and Taylor, J. E. (2016). Exact post-selection inference with the lasso. The Annals of Statistics 44, 907–927. [Google Scholar]
-
Negahban, S., Yu, B., Wainwright, M. J. and Ravikumar, P. K. (2009). A unified framework for high-dimensional analysis of
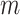 -estimators with decomposable regularizers. In: Advances in Neural Information Processing Systems. pp. 1348–1356. [Google Scholar]
-estimators with decomposable regularizers. In: Advances in Neural Information Processing Systems. pp. 1348–1356. [Google Scholar] - Ongen, H., Buil, A., Brown, A. A., Dermitzakis, E. T. and Delaneau, O. (2015). Fast and efficient QTL mapper for thousands of molecular phenotypes. Bioinformatics 32, 1479–1485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panigrahi, S. (2018). Carving model-free inference. arXiv preprint, arXiv:1811.03142. [Google Scholar]
- Panigrahi, S., Taylor, J. and Weinstein, A. (2016). Pliable methods for post-selection inference under convex constraints. arXiv preprint, arXiv:1605.08824. [Google Scholar]
- Panigrahi, S., Markovic, J. and Taylor, J. (2017). An MCMC-free approach to post-selective inference. arXiv preprint, arXiv:1703.06154. [Google Scholar]
- Reid, S. and Tibshirani, R. (2016). Sparse regression and marginal testing using cluster prototypes. Biostatistics 17, 364–376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schadt, E. E.,, Monks, S. A.,, Drake, T. A.,, Lusis, A. J.,, Che, N.,, Colinayo, V.,, Ruff, T. G.,, Milligan, S. B.,, Lamb, J. R.,, Cavet, G. and others (2003). Genetics of gene expression surveyed in maize, mouse and man. Nature 422, 297. [DOI] [PubMed] [Google Scholar]
- Simes, R. J. (1986). An improved Bonferroni procedure for multiple tests of significance. Biometrika 73, 751–754. [Google Scholar]
- Storey, J. D. (2003). The positive false discovery rate: a Bayesian interpretation and the q-value. The Annals of Statistics 31, 2013–2035. [Google Scholar]
- Tian, X.,, Taylor, J. (2018). Selective inference with a randomized response. The Annals of Statistics 46, 679–710. [Google Scholar]
- Zhong, H. and Prentice, R. L. (2008). Bias-reduced estimators and confidence intervals for odds ratios in genome-wide association studies. Biostatistics 9, 621–634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou, H. and Hastie, T. (2005). Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society: Series B 67, 301–320. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.