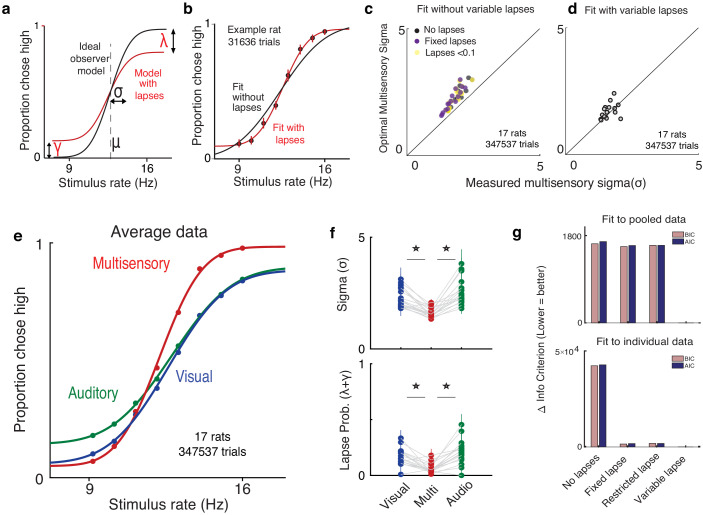
Figure 2. Deviations from ideal observer reflect lapses in judgment.

(a) Schematic psychometric performance of an ideal observer (black) vs. a model that includes lapses (red). The ideal observer model includes two parameters: midpoint (μ) and inverse slope (σ). The four-parameter model includes μ, σ, and lapse probabilities for low-rate (γ) and high-rate choices (λ). Dotted line shows the true category boundary (12.5 Hz). (b) Subject data was fit with a two-parameter model without lapses (black) and a four-parameter model with lapses (red). (c and d) Ideal observer predictions vs. measured multisensory sigma for fits with and without variable lapses across conditions. (c) Multisensory integration seems supra-optimal if lapses are not accounted for (no lapses, black), fixed across conditions (fixed lapses, purple), or assumed to be less than 0.1 (restricted lapses, yellow). (d) Optimal multisensory integration is restored when allowing lapses to vary freely across conditions (n = 17 rats. Points represent individual rats. Data points that lie on the unity line represent cases in which the measured sigma was equal to the optimal prediction). (e) Rats’ psychometric curves on auditory (green), visual (blue), and multisensory (red) trials. Points represent data pooled across 17 rats, and lines represent separate four-parameter fits to each condition. (f) Fit values of sigma (top) and lapse parameters (bottom) on unisensory and multisensory conditions. Both parameters showed significant reduction on the multisensory conditions (paired t-test, p<0.05); n = 17 rats (347,537 trials). (g) Model comparison using Bayes Information Criterion (pink) and Akaike Information Criterion (blue) for fits to pooled data across subjects (top) and to individual subject data (bottom). Lower scores indicate better fits. Both metrics favor a model where lapses are allowed to vary freely across conditions (‘Variable lapse’) over one without lapses (‘No lapses’), one with a fixed probability of lapses (‘Fixed lapse’), or where the lapses are restricted to being less than 0.1 (‘Restricted lapse’).