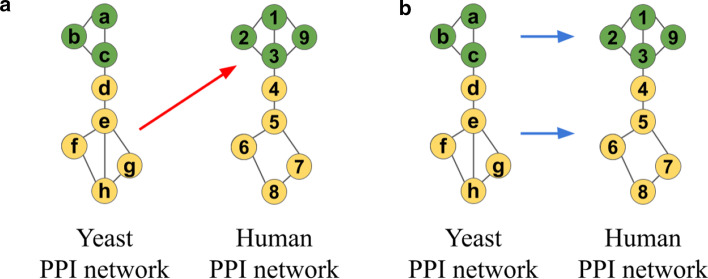
Fig. 1.
Illustration of topological similarity versus relatedness. Suppose that: (i) PPI networks of yeast and human are being aligned, (ii) the toy networks shown are parts of the full networks, (iii) each node performs either the “green” or “yellow” function, and (iv) because of incompleteness/noisiness of PPI network data or molecular evolutionary events such as gene mutation, duplication or deletion the green functional module in human (nodes 1, 2, 3, and 9) has an extra protein compared to the green module in yeast (nodes a, b, and c), and the yellow module in yeast has an extra interaction compared to the yellow module in human. a A topological similarity-based NA method will align yellow nodes e, f, g, and h in yeast to green nodes 1, 2, 3, and 9 in human, because both node sets form the same subgraph—a square with a diagonal, i.e., because the set of yellow nodes in yeast are topologically more similar to the set of green nodes in human than to the set of yellow nodes in human. However, this alignment is functionally incorrect because yellow and green nodes perform different functions. b Instead, our NA framework based on topological relatedness will use the topological and functional data to learn that a triangle in yeast (a, b, and c) should be aligned to a square-with-diagonal in human (1, 2, 3, and 9) because both perform the same function (green), and that a square-with-diagonal in yeast (e, f, g, and h) should be aligned to a square in human (5, 6, 7, and 8) because both perform the same function (yellow). Then, in other parts of the networks, our framework will try to align these learned patterns, to transfer knowledge between them