Functional survival forests for multivariate longitudinal outcomes: Dynamic prediction of Alzheimer’s disease progression

Abstract

The random survival forest (RSF) is a non-parametric alternative to the Cox proportional hazards model in modeling time-to-event data. In this article, we developed a modeling framework to incorporate multivariate longitudinal data in the model building process to enhance the predictive performance of RSF. To extract the essential features of the multivariate longitudinal outcomes, two methods were adopted and compared: multivariate functional principal component analysis and multivariate fast covariance estimation for sparse functional data. These resulting features, which capture the trajectories of the multiple longitudinal outcomes, are then included as time-independent predictors in the subsequent RSF model. This non-parametric modeling framework, denoted as functional survival forests, is better at capturing the various trends in both the longitudinal outcomes and the survival model which may be difficult to model using only parametric approaches. These advantages are demonstrated through simulations and applications to the Alzheimer’s Disease Neuroimaging Initiative.

1. Introduction

Alzheimer’s disease (AD) is a progressive, neurodegenerative disease leading to the inhibition of memory and other mental functions.^1,2 At present, no cure exists for AD, however, medications and other treatments may temporarily improve the symptoms when administered early in the disease process.¹ Mild cognitive impairment (MCI) is often regarded as a risk state of AD with 32% of patients diagnosed with MCI progressing to Alzheimer’s dementia within five years.^3,4 As such, it is of interest to build prognostic models that are robust in predicting conversion of MCI to AD prior to complete disease onset, as this would allow physicians to adopt earlier intervention strategies. In this study, we examine the Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset, which is a longitudinal study effort to collect clinical, imaging, genetic, and other biomarker data to track the progression of AD patients.

Modeling of AD progression based on accumulated longitudinal information leads to notable improvement in predicting survival risk as shown in multiple studies. For example, the joint modeling (JM) framework for longitudinal and survival data was used to show that the Alzheimer’s Disease Assessment Scale-Cognitive 13 (ADAS-Cog13) subtest is an important indicator of conversion from MCI to AD in the context of dynamic prediction.⁵ Using dynamic prediction allows for model assessment at different points in time as new longitudinal measurements become available. It demonstrates the advantage of including the most current information in making more accurate disease prognosis.⁶ A JM approach can also be used when considering multiple longitudinal outcomes, however, this may be computationally challenging as the number of longitudinal outcomes increases.⁷ Li and Luo⁸ proposed a two-staged model named MFPCCox which achieves better predictive performance compared to JM and has significantly faster computational times. In the first step, they considered the multivariate longitudinal outcomes as functional data and applied multivariate functional principal component analysis (MFPCA).⁹ The principal component scores extracted by MFPCA act as orthogonal features of the longitudinal outcomes, which addresses autocorrelation within a longitudinal outcome as well as potential correlation between multiple longitudinal outcomes. In the subsequent step, the principal component scores were included as time-independent covariates with other baseline measurements in a Cox proportional hazards model.

However, the MFPCCox framework could be improved in several aspects. To deal with sparse functional data, Li et al.¹⁰ proposed a multivariate fast covariance estimation (mFACEs) method which also extracts features from multiple longitudinal outcomes. They suggested that when the data are not sufficiently dense, MFPCA may not fully capture the cross-correlation between outcomes. This is because MFPCA estimates the cross-correlation between outcomes from the scores of univariate FPCA which are shrunk toward zero as the data become sparse. In addition, the Cox proportional hazards model may not be appropriate when the assumption of proportional hazards is not met. In contrast, fully non-parametric survival models are not restricted by this assumption and may be more robust to model misspecification. Many non-parametric machine learning algorithms, including random forests, have been extended to the survival setting.^11,12 The random survival forest (RSF) implemented by Ishwaran et al.¹² is an ensemble method for survival analysis that is constructed by averaging over the predicted hazards of many decision trees. They demonstrated that survival ensembles remain stable in the high-dimensional setting and have consistent prediction error even in the presence of additional noise covariates. In comparison, the prediction error of the Cox model grew progressively higher as additional noise covariates increased the dimensionality. RSF was also shown to be more robust in detecting unspecified interactions¹³ and patterns of non-linearity in the covariates.¹⁴ Although random forests have been well studied in cross-sectional data, less work has been done in incorporating longitudinal data into the random forest model. Some recent approaches include a semi-parametric mixed-effects model where the non-parametric part is modeled using random forests.¹⁵ To the best of our knowledge, no prior research has considered multiple longitudinal outcomes in random forests for survival analysis.

In this article, we developed a functional survival forests framework to incorporate multiple longitudinal outcomes by first extracting features of the longitudinal outcomes using functional principal component analysis methods. The features will be included as covariates in the proceeding survival model. Both mFACEs and RSF are investigated as alternatives to each of the steps of the two-stage model used in MFPCCox. We demonstrate that this framework performs better than parametric models in capturing the various trends in both the longitudinal outcomes and the survival model. A major aim of this study is to use functional survival forests to refine the predictive modeling of AD progression by making use of the longitudinal information available from the ADNI dataset.

This article is organized as follows. In Section 2, we describe the MFPCA and mFACEs methods for feature extraction from multiple longitudinal markers. Then, we compare the RSF and Cox models. We also establish the details of the dynamic prediction setting for the simulation and real data analysis sections. In Section 3, we conduct a simulation study to assess the performance of the RSF and Cox models in conjunction with the MFPCA and mFACEs methods for incorporating multiple longitudinal outcomes. In Section 4, we apply the proposed functional survival forest to the ADNI dataset. In Section 5, we discuss the results and make some concluding remarks.

2. Methods

Consider a study setting where I patients are enrolled. Each ith (i = 1, …, I) patient is followed from the start of the study for J_i visits until their observed event time $T_i^{*}=\text{min}\left(T_i,C_i\right)$, where T_i is the true event time, and C_i is the censoring time independent from T_i and the patients’ covariates. The event indicator, δ_i = I(T_i ≤ C_i), denotes whether or not the observed time was censored. Baseline (time-independent) covariates were collected from each patient at the study onset. Denote this set of P covariates by the matrix Z_I×P. In addition, at each follow-up visit, Q longitudinal measures were also collected from each patient. Let Y_iq(t_ij) refer to the observed values for the qth measure for subject i at visit number j.

2.1. Longitudinal data analysis

2.1.1. Multivariate functional principal component analysis

First, we briefly describe the formulation of the univariate and multivariate FPCA methods.^9,16 Consider a single longitudinal outcome q with trajectory X_iq(t). Denote its unknown smoothed mean function as μ_q(t) and autocorrelation between time points t and t′ as the covariance function Σ_q(t, t′) = cov{X_iq(t), X_iq(t′)}. The covariance function can be rewritten using spectral decomposition as ${\Sigma }_q\left(t,t^{\prime }\right)=\sum _{m=1}^{\infty }{\lambda }_{qm}{\varphi }_{qm}(t){\varphi }_{qm}\left(t^{\prime }\right)$, where {λ_qm} is the set of non-increasing eigenvalues and {ϕ_qm(t)} are the corresponding eigenfunctions. The Karhunen–Loeve theorem gives the following expansion of X_iq(t)

$$X_{iq}(t)={\mu }_q(t)+\sum _{m=1}^{\infty }{\xi }_{iqm}{\varphi }_{qm}(t)$$ (1)

where ξ_iqm is the set of uncorrelated functional principal component scores with mean zero and variance λ_qm. Furthermore, the longitudinal trajectory (1) can be sufficiently approximated using the first M_q eigenfunctions, $X_{iq}(t)\approx {\mu }_q(t)+{\sum }_{m=1}^{M_q}{\xi }_{iqm}{\varphi }_{qm}(t)$. The value of M_q can be selected based on a predetermined percentage of variance explained (PVE).¹⁶ In practice, we do not observe X_iq(t) but instead observe Y_iq(t_ij) = X_iq(t_ij) + ϵ_iq(t_ij) at each jth visit, where ϵ_iq(t_ij) is noise assumed to be normally distributed. Therefore, the univariate FPCA is conducted using the Principal Analysis by Conditional Estimation (PACE) algorithm.¹⁶ The PACE algorithm is able to estimate the mean function ${\widehat{\mu }}_q(t)$, error variance ${\widehat{\sigma }}_q$, covariance function ${\widehat{\Sigma }}_q\left(t,t^{\prime }\right)$, eigenvalues ${\widehat{\lambda }}_{qm}$, and eigenfunctions ${\widehat{\varphi }}_{qm}(t)$. Using these estimated values, we can calculate the estimated FPC scores of a given subject by

$${\widehat{\xi }}_{iqm}={\widehat{\lambda }}_{qm}{\left({\widehat{\varphi }}_{iqm}\right)}^T{\widehat{\Sigma }}_{Y_{iq}}^{-1}\left(Y_{iq}-{\widehat{\mu }}_q\right)$$ (2)

where $Y_{iq}={\left\{Y_{iq}\left(t_{ij}\right)\right\}}_{j=1,\dots ,J_i}$, ${\widehat{\mu }}_{iq}={\left\{{\widehat{\mu }}_{iq}\left(t_{ij}\right)\right\}}_{j=1,\dots ,J_i}$, ${\widehat{\varphi }}_{iqm}={\left\{{\widehat{\varphi }}_{iqm}\left(t_{ij}\right)\right\}}_{j=1,\dots ,J_i}$, and ${\widehat{\Sigma }}_{Y_{iq}}$ is a J_i × J_i matrix with the (j,j′) entry defined as ${\left({\widehat{\Sigma }}_{Y_{iq}}\right)}_{j{j}^{\prime }}={\widehat{\Sigma }}_q\left(t_{ij},t_{i{j}^{\prime }}\right)+{\widehat{\sigma }}_q^2{\delta }_{j{j}^{\prime }},{\delta }_{j{j}^{\prime }}=1$ for j = j′ and 0 otherwise.

However, in the multivariate case, there exists non-negligible correlation that arises among longitudinal outcomes. Therefore, the set of scores derived for each longitudinal outcome (2) may be inter-correlated. MFPCA extends the univariate FPCA methodology in a second step by modeling the correlations between FPC scores for each of the Q longitudinal outcomes. Denote the total number of univariate FPC scores as $M_{+}={\sum }_{q=1}^Q{M}_q$. Let Θ be the I × M₊ matrix where each row is a subject-specific vector concatenating the univariate FPC scores for each outcome. Performing eigenanalysis on the matrix $H_{M_{+}\times M_{+}}={(n-1)}^{-1}{\Theta }^T\Theta$ gives the resulting orthonormal eigenvectors ${\left\{{\widehat{c}}_k\right\}}_{k=1,\dots ,M_{+}}$ and respective eigenvalues ${\left\{{\widehat{v}}_k\right\}}_{k=1,\dots ,M_{+}}$. The estimated multivariate eigenfunctions is given by ${\widehat{\psi }}_{qk}(t)=\sum _{m=1}^{M_q}{\left[{\widehat{c}}_k\right]}_m^{(q)}{\widehat{\varphi }}_{qm}(t)$. Then, the estimated MFPC scores for the ith subject can be calculated using the univariate FPC scores and the qth block of ${\widehat{c}}_k$ denoted ${\left[{\widehat{c}}_k\right]}^{(q)}$ by the following

$${\widehat{\rho }}_{ik}=\sum _{q=1}^Q\sum _{m=1}^{M_q}{\left[{\widehat{c}}_k\right]}_m^{(q)}{\widehat{\xi }}_{iqm}$$ (3)

Lastly, the qth longitudinal outcome, X_iq(t), can be sufficiently approximated by

$${\widehat{X}}_{iq}(t)\approx {\widehat{\mu }}_q(t)+\sum _{k=1}^D{\widehat{\rho }}_{ik}{\widehat{\psi }}_{qk}(t)$$ (4)

where D < M₊ is selected based on PVE or other information criteria.

2.1.2. mFACEs for sparse functional data

Next, we introduce the mFACEs method to generate scores from the multiple longitudinal outcomes.¹⁰ The main idea of mFACEs is to estimate the covariance functions C_qq′ (s, t) = cov{X_iq(s), X_iq′(t)} by using bivariate penalized splines. Note that Cqq_′ simultaneously accounts for both autocorrelation within an outcome as well as cross-correlation between outcomes. This contrasts with the two-step MFPCA approach in Section 2.1.1 which accounts for the autocorrelation of each individual longitudinal outcome in the first step and the correlation between univariate FPC scores in the second step. When functional data are sparse, the univariate FPC scores are shrunk toward zero.¹⁰ Therefore, MFPCA may not sufficiently capture the cross-correlation between outcomes. In comparison, mFACEs estimates the covariance within and between outcomes in the same step, leading to better covariance estimates in the presence of sparse functional data.

To estimate C_qq′, first define the residuals as $r_{ij}^{(q)}=Y_q\left(t_{ij}\right)-{\mu }_q\left(t_{ij}\right)$. Let the auxiliary variables be defined as $C_{i{j}_1{j}_2}^{\left(q{q}^{\prime }\right)}=r_{i{j}_1}^{(q)}{r}_{i{j}_2}^{\left(q^{\prime }\right)}$. In practice, the mean functions, μ_q(t), are not known and are estimated using P-splines with the penalties selected using leave-one-out cross-validation.¹⁷ Thus, with the estimated mean ${\widehat{\mu }}_q(t)$, we have ${\widehat{r}}_{ij}^{(q)}=Y_q\left(t_{ij}\right)-{\widehat{\mu }}_q\left(t_{ij}\right)$ and ${\widehat{C}}_{i{j}_1{j}_2}^{\left(q{q}^{\prime }\right)}={\widehat{r}}_{i{j}_1}^{(q)}{\widehat{r}}_{i{j}_2}^{\left(q^{\prime }\right)}$. The auxiliary variables are noisy but unbiased estimates of the covariance functions whenever q ≠ q′ and j₁ ≠ j₂, that is, $\mathbb{E}\left(C_{i{j}_1{j}_2}^{\left(q{q}^{\prime }\right)}\right)=C_{q{q}^{\prime }}\left(t_{i{j}_1}^q,t_{i{j}_2}^{q^{\prime }}\right)+{\sigma }_q^2{1}_{\left(q=q^{\prime },j_{1=}{j}_2\right)}$. Next, the noisy auxiliary variables are smoothed using bivariate P-splines¹⁸ to get estimates of the covariance functions. Lastly, all the estimates of the individual covariance functions are pooled together and eigendecomposition is applied to obtain a properly defined (positive semi-definite) covariance operator.

The bivariate P-splines model C_qq′(s, t) uses tensor-product splines defined as

$$G_{q{q}^{\prime }}(s,t)=\sum _{1\le {\gamma }_1,{\gamma }_2\le c}{\theta }_{{\gamma }_1,{\gamma }_2}^{q{q}^{\prime }}{B}_{{\gamma }_1}(s)B_{{\gamma }_2}(t)$$

where ${\Theta }_{q{q}^{\prime }}={\left[{\theta }_{{\gamma }_1,{\gamma }_2}^{q{q}^{\prime }}\right]}_{1\le {\gamma }_1,{\gamma }_2\le c}$ is the coefficient matrix and B is the collection of B-spline basis functions. Denote c as the number of knots plus order of the B-splines.

The estimate $\widehat{\Theta }$ which minimizes the penalized least squares is used to estimate the coefficient matrix of the cross-covariance function, Θ_qq′, and the auto-covariance function, Θ_qq. The penalized least squares for Θ_qq′ is given by

$$\sum _{i=1}^n\sum _{j_1=1}^{m_{iq}}\sum _{j_2=1}^{m_{i{q}^{\prime }}}{\left\{G_{q{q}^{\prime }}\left(t_{i{j}_1}^{(q)},t_{i{j}_2}^{\left(q^{\prime }\right)}\right)-{\widehat{C}}_{i{j}_1{j}_2}^{\left(q{q}^{\prime }\right)}\right\}}^2+{\lambda }_{q{q}^{\prime }1}{\Vert D{\Theta }_{q{q}^{\prime }}\Vert }^2+{\lambda }_{q{q}^{\prime }2}{\Vert D{\Theta }_{q{q}^{\prime }}^T\Vert }^2$$

Here, λ_qq′1 and λ_qq′2 are non-negative smoothing parameters. An algorithm for the automatic selection of these smoothing parameters is described.¹⁰ The column and row penalties, ∥DΘ_qq′∥² and ${\Vert D{\Theta }_{q{q}^{\prime }}^T\Vert }^2$, respectively, penalize the second order partial derivatives of G_qq′(s, t) along the s and t directions, with the two smoothing parameters controlling the different levels of smoothness in these directions.

The penalized least squares for the auto-covariance function Θ_qq is defined similarly by the following. Note that the penalty terms are the same when Θ_qq is symmetric so only one smoothing parameter is required

$$\sum _{i=1}^n\sum _{j_1=1}^{m_{iq}}\sum _{j_2=1}^{m_{iq}}{\left\{G_{qq}\left(t_{i{j}_1}^{(q)},t_{i{j}_2}^{(q)}\right)+{\sigma }_q^2{1}_{\left\{j_1=j_2\right\}}-{\widehat{C}}_{i{j}_1{j}_2}^{(qq)}\right\}}^2+{\lambda }_q{\Vert D{\Theta }_{qq}\Vert }^2$$

Proposition 1 in Li et al.¹⁰ shows that obtaining the estimate ${\widehat{\Theta }}_{q{q}^{\prime }}$ is sufficient for deriving the principal component scores for the ith subject. Similar to MFPCA, the first D ≥ 1 scores, ${\widehat{\rho }}_{ik}$, where k = 1, …, D can be selected as an approximation, using PVE as a cutoff criterion.

We denote the principal component scores vector for both MFPCA and mFACEs as ${\widehat{\rho }}_i=\left\{{\widehat{\rho }}_{i1},\dots ,{\widehat{\rho }}_{iD}\right\}$.

2.2. Survival data analysis

In the second step, several survival models were built using the scores derived from the longitudinal data. The estimated scores, ${\widehat{\rho }}_i$, are included into the models as time-independent covariates. We focused on the Cox model and the RSF¹² to estimate the risk of disease progression. In the Cox model, the hazard function for the ith subject is defined as

$$h_i(t)=h_0(t)\text{exp}\left\{Z_i^T\gamma +{\widehat{\rho }}_i^T\beta \right\}$$

where Z_i are the baseline/time-independent covariates with corresponding regression coefficients γ_p×1, and ${\widehat{\rho }}_i$ are the scores derived from longitudinal outcomes with corresponding regression coefficients β_D×1. While the Cox model is flexible due to its baseline hazard function which can take any form, it must satisfy the proportional hazards assumption.

In comparison, the RSF is a non-parametric survival model constructed by aggregating an ensemble of survival trees. To define the hazard function for the RSF, we first outline its construction. To begin, B bootstrap samples are drawn with replacement from the original data. Each bootstrap sample is drawn to the same size as the original data and on average excludes 37% of the data. The excluded data are called “out-of-bag” (OOB) data and may be set aside for testing purposes later. For each of the B samples, a survival tree is grown. At each node, a fixed number of candidate variables are randomly selected from the union of the time-independent covariates, Z, and the scores of the longitudinal outcomes, $\widehat{\rho }$. The node is split using the variable and split value that maximizes the survival difference between daughter nodes. Thus, as the tree is grown, dissimilar cases are pushed apart. Survival difference can be quantified in several ways. Here, we split nodes based on the log-rank test statistic.^19,20 Another option is to use the standardized log-rank score statistic proposed by Hothorn and Lausen.²¹ The tree is grown by repeating this step until the condition that each terminal node should have at least d₀ > 0 unique deaths is satisfied. These procedures result in a tree with terminal nodes populated by subjects who have relatively homogeneous survival outcomes. The cumulative hazard function (CHF) for the kth terminal node of a single survival tree is given by the Nelson–Aalen estimator and every member of the terminal node shares the same hazard. The CHF is ${\widehat{H}}_k(t)={\sum }_{t_{jk}\le t}\frac{d_{jk}}{R_{jk}}$, where d_jk is the number of events at time t_jk and R_jk is the number of individuals at risk at time t_jk. The ensemble CHF for the ith subject can be found by dropping the subject through all B trees and averaging the hazard obtained from each tree. Denote the ensemble CHF as H_e(t|x_i) and the CHF from the bth bootstrap tree as H_b(t|x_i). Then, the ensemble CHF is given by

$$H_e\left(t\mid x_i\right)=\frac{1}{B}\sum _{b=1}^B{H}_b\left(t\mid x_i\right)$$ (5)

with its corresponding survival function S(t) = e^−CHF.

While the RSF algorithm allows for the mapping of covariates to survival time in a non-linear fashion, this complexity also makes the interpretation of covariates more difficult in comparison to the Cox model. To this end, variable importance (VIMP) is a metric that can be calculated for forest-like structures to still allow for the identification and ranking of variables based on predictive ability. For a particular variable x, the VIMP for RSF is calculated by randomly permuting the values of x, breaking up its relationship with the survival outcome. Each subject is subsequently dropped down the trees where they are OOB. The CHF from each tree is calculated from the procedure detailed above. Thus, if a variable contributes significantly to the model, this would be reflected in a difference in the CHF as its values would be shuffled. The VIMP for variable x is defined as the difference between the prediction error (estimated by the concordance index or c-index) of the original ensemble and the prediction error of the ensemble that permutes the values of x. One should be cautious not to interpret VIMP as the effect of x on the prediction error when it is shuffled, but as the change in prediction error of a new subject if x were to be made uninformative.

2.3. Dynamic predictions

Prognosis is usually given in terms of the probability that an event will occur in a given prediction window. We evaluate the performance of the survival models using dynamic prediction which allows for updating the prognosis as new longitudinal measurements are made available. First, the dataset was split into training and testing sets. The full longitudinal trajectories and baseline values of subjects in the training set were used to build the model. Model performance was assessed using the testing set at landmark times of clinical interest. For each subject, still event-free at landmark time t, define ${\widehat{\rho }}_i^{(t)}$ as the scores of their longitudinal outcomes calculated based on their observations up to time t using the functional principal component transformations determined from the training set. The scores ${\widehat{\rho }}_i^{(t)}$ and their baseline measurements were passed to the fitted survival model to determine subject’s risk. Let t′ = t + Δt be a future prediction time of interest and recall that S(t) = e^−CHF. To calculate the predicted risk of an event occurring within the window (t, t′], we determine the conditional probability of being event-free at time t′ given that the subject was event-free at time t, denoted by ${\widehat{\pi }}_i\left(t^{\prime }\mid t\right)=p\left(T_i^{*}\ge t^{\prime }\mid T_i^{*}\ge t,Z_i,{\widehat{\rho }}_i^{(t)}\right)=\frac{S_i\left(t^{\prime }\right)}{S_i(t)}$.

Model performance is evaluated in terms of both discrimination and calibration. Discrimination refers to how well the model identifies the subjects who experienced the event versus the subjects who did not experience the event. This was measured using the time-dependent area under the curve (AUC).^22,23 Although the concordance index (c-index) is another popular discrimination measure for survival data, the time-dependent AUC has been shown to be a more proper scoring metric for t-year predicted risks.²⁴ The c-index does not give a value for a specific time horizon of prediction and is therefore unable to determine if a model performs better at a certain time horizon versus another. Calibration refers to the agreement between the predicted risks and true risks. Both discrimination and calibration are measured by the dynamic expected Brier score (BS).²² To adjust for right censoring, the Kaplan–Meier method was used as the inverse probability of censoring weights estimator. Better predictive performance is indicated by a higher AUC and lower BS. AUC and BS are calculated for different combinations of t and Δt.

These methods are implemented in R. Example code is provided in the supplementary material to facilitate easy implementation.

3. Simulation study

The performance of the proposed methods was evaluated using simulated data emulating the ADNI dataset analyzed in Section 4. In this section, we assess the predictive performance of functional survival forests by comparing MFPCA versus mFACEs to handle the longitudinal outcomes and RSF versus Cox to model the survival outcome.

We simulated 100 datasets each with a sample size of I = 300 subjects. Each subject had Q = 3 longitudinal covariates with a maximum of J_i = 21 visits from times [0, 10] with a time interval of 0.5. The longitudinal measurements, denoted Y_iq(t_ij), were simulated from the following longitudinal submodels

$$Y_{iq}\left(t_{ij}\right)=X_{iq}\left(t_{ij}\right)+{ϵ}_{iq}\left(t_{ij}\right),\text{\hspace{1em} where }{X}_{iq}\left(t_{ij}\right)={\beta }_{0q}+{\beta }_{1q}{x}_{iq}+{\beta }_{tq}{t}_{ij}+b_{iq}\text{\hspace{1em} and \hspace{1em}}j=1\dots J$$

We set β_0q = [1.5, 2, 0.5], β_1q = [2, −1, 1], and β_tq = [1.5, −1, 0.6]. The scalar covariate was generated from x_iq~N(3, 1). The subject-specific random effects b_iq were generated from the multivariate normal distribution, MVN(0, Σ), where

$$\Sigma =\left[\begin{array}{ccc}{\sigma }_1^2& {\eta }_{12}{\sigma }_1{\sigma }_2& {\eta }_{13}{\sigma }_1{\sigma }_3\\ & {\sigma }_2^2& {\eta }_{23}{\sigma }_2{\sigma }_3\\ & & {\sigma }_3^2\end{array}\right]$$

We set [σ₁, σ₂, σ₃] = [1, 1.5, 2] and [η₁₂, η₁₃, η₂₃] = [−0.2, 0.1, −0.3]. Lastly, ϵ_iq(t_ij) was generated from N(0, 1).

We define the survival submodel by the following hazard function

$$h_i(t)=h_0(t)\text{exp}\left[\gamma Z_i+\sum _{q=1}^3{\alpha }_q{X}_{iq}\left(t_{ij}\right)\right]$$ (6)

where h₀(t) = exp(−7). We set γ = [−4,−2] and generated two time-independent covariates, Z_i = [z_i1, z_i2], where z₁~Bin(p = 0.5) and z₂~N(0, 1). Lastly, the coefficients for the true longitudinal trajectories, α, were set as [0.2, −0.2, 0.4]. The survival function is given by $S_i(t)=\text{exp}\left[-{\int }_0^t{h}_i(u)du\right]$. Then, the survival times can be generated by passing the standard uniform distribution through the inverse probability integral transformation of the survival function. Censoring times were simulated independent of survival times from a uniform distribution, U(1, 22), resulting in a censoring rate of approximately 30%.

In each simulated dataset, we randomly selected 200 patients for training the model and reserved the remaining 100 for testing and evaluating the model performance. The simulated longitudinal trajectories, Y_iq(t_ij), were analyzed using both the MFPCA and mFACEs methods. Three principal components were chosen to account for 95% of the variation in the longitudinal outcomes. The scores obtained from these methods were then used as predictors together with other time-independent covariates in the RSF and Cox models. The RSF was built using 1000 trees and the following default parameters. At each node, the number of predictors considered for the split was set to the square root of the total number of predictors. The tree was grown until each terminal node contained at least 15 patients. We denote this simulation setting as Scenario 1.

In Scenario 2, we illustrated how the predictive performance may be affected under model misspecification. We added the interaction, Z_i = [z_i1, z_i2, z_i1 · z_i2], as an additional baseline variable in simulating event times and set the coefficients as γ = [−4, −2, 4]. The interaction term was omitted when specifying the predictors to be included in the RSF and Cox models. Scenario 2 evaluates the models’ capability to capture the interaction effect without it being explicitly stated.

After fitting the proposed models on the training set, dynamic prediction was performed using the testing set. For each subject in the testing set, the longitudinal data up until the landmark time t were used to estimate the FPC scores, which were used in the fitted model to predict the subject-specific survival probability ${\widehat{\pi }}_i(t+\Delta t\mid t)$ at some future time point, t + Δt. In our analysis, we considered Δt = [1, 2] at time points t = [1, 2, 3, 4]. The predictive performance was evaluated at each time point using the time-dependent AUC to assess discrimination and the time-dependent BS to assess calibration. For comparison, the true AUC was calculated at each t + Δt from the true cumulative hazard values derived by integrating⁶ over time.

In Scenario 1 (Table 1), the AUC from the Cox model closely matches the true AUC, suggesting that both MFPCA and mFACEs can successfully extract the predictive features of the multivariate longitudinal trajectories. In comparison, the RSF model has AUC that is close to the true AUC and BS slightly higher than the BS from the Cox model counterpart. This is expected as the true survival submodel in the data simulation process was specified using the Cox model. However, in Scenario 2 (Table 2), the AUC of the Cox model drops dramatically when the model was purposefully misspecified to not include the interaction term. The BS is also higher in comparison to its RSF counterpart. The AUC from RSF remains close to the true AUC despite the model misspecification. These results suggest that RSF is able to account for interaction effects not explicitly specified in the model. The better results of RSF in terms of AUC and BS in Table 2 suggest that RSF is able to account for non-linear relationships between covariates, leading to more robust predictive performance under model misspecification. Models that used MFPCA to obtain scores also seemed to perform slightly better than models that used mFACEs in both scenarios. A graphical comparison of the AUC is provided in Figures S1 and S2 of the supplementary material.

Table 1.

Scenario 1: survival data were simulated from a joint model with two baseline covariates and three longitudinal outcomes.

			RSF		Cox
t	Δt	True AUC	AUC	BS	AUC	BS
MFPCA
1	1	0.929(0.050)	0.898(0.060)	0.054(0.017)	0.927(0.050)	0.044(0.016)
1	2	0.938(0.033)	0.906(0.046)	0.087(0.019)	0.934(0.034)	0.067(0.020)
2	1	0.924(0.050)	0.878(0.066)	0.062(0.021)	0.920(0.051)	0.051(0.019)
2	2	0.930(0.045)	0.892(0.053)	0.101(0.022)	0.927(0.045)	0.077(0.023)
3	1	0.915(0.056)	0.871(0.072)	0.072(0.022)	0.915(0.059)	0.059(0.019)
3	2	0.923(0.036)	0.879(0.045)	0.119(0.028)	0.920(0.037)	0.090(0.025)
4	1	0.903(0.055)	0.832(0.089)	0.086(0.029)	0.899(0.056)	0.070(0.025)
4	2	0.918(0.042)	0.867(0.057)	0.140(0.031)	0.914(0.042)	0.106(0.031)
mFACEs
1	1	0.929(0.050)	0.890(0.064)	0.056(0.017)	0.926(0.051)	0.045(0.016)
1	2	0.938(0.033)	0.896(0.050)	0.092(0.019)	0.934(0.035)	0.067(0.020)
2	1	0.924(0.050)	0.865(0.076)	0.063(0.021)	0.919(0.052)	0.051(0.020)
2	2	0.930(0.045)	0.872(0.066)	0.109(0.024)	0.925(0.048)	0.079(0.024)
3	1	0.915(0.056)	0.843(0.097)	0.076(0.022)	0.913(0.063)	0.061(0.020)
3	2	0.923(0.036)	0.859(0.062)	0.130(0.031)	0.918(0.039)	0.094(0.027)
4	1	0.903(0.055)	0.812(0.095)	0.090(0.029)	0.896(0.055)	0.073(0.026)
4	2	0.918(0.042)	0.846(0.069)	0.152(0.033)	0.910(0.044)	0.111(0.031)

AUC and BS are averaged across 100 simulated datasets with standard deviations provided in subscripts.

RSF, random survival forest; AUC, area under the curve; BS, Brier score; MFPCA, multivariate functional principal component analysis; mFACEs, multivariate fast covariance estimation.

Table 2.

Scenario 2: survival data were simulated from a joint model with two baseline covariates with their interaction and three longitudinal outcomes.

			RSF		Cox
t	Δt	True AUC	AUC	BS	AUC	BS
MFPCA
1	1	0.930(0.047)	0.880(0.084)	0.052(0.016)	0.849(0.096)	0.057(0.018)
1	2	0.940(0.034)	0.905(0.052)	0.081(0.019)	0.857(0.073)	0.093(0.020)
2	1	0.924(0.061)	0.877(0.082)	0.058(0.020)	0.838(0.123)	0.061(0.020)
2	2	0.932(0.047)	0.899(0.057)	0.095(0.023)	0.833(0.075)	0.108(0.024)
3	1	0.916(0.057)	0.865(0.093)	0.071(0.022)	0.808(0.108)	0.075(0.024)
3	2	0.925(0.039)	0.886(0.050)	0.113(0.029)	0.807(0.074)	0.128(0.031)
4	1	0.906(0.056)	0.846(0.077)	0.083(0.028)	0.774(0.125)	0.087(0.028)
4	2	0.916(0.039)	0.869(0.048)	0.132(0.028)	0.773(0.084)	0.151(0.035)
mFACEs
1	1	0.930(0.047)	0.863(0.090)	0.056(0.017)	0.837(0.093)	0.058(0.018)
1	2	0.940(0.034)	0.886(0.058)	0.093(0.021)	0.845(0.077)	0.097(0.023)
2	1	0.924(0.061)	0.856(0.103)	0.062(0.020)	0.827(0.126)	0.063(0.020)
2	2	0.932(0.047)	0.874(0.056)	0.111(0.023)	0.825(0.074)	0.116(0.028)
3	1	0.916(0.057)	0.843(0.085)	0.078(0.022)	0.803(0.102)	0.080(0.026)
3	2	0.925(0.039)	0.859(0.061)	0.132(0.030)	0.796(0.077)	0.143(0.040)
4	1	0.906(0.056)	0.821(0.088)	0.089(0.029)	0.760(0.125)	0.096(0.034)
4	2	0.916(0.039)	0.842(0.060)	0.154(0.033)	0.767(0.086)	0.175(0.052)

The interaction term was not specified in the model. AUC and BS are averaged across 100 simulated datasets with standard deviations provided in subscripts.

RSF, random survival forest; AUC, area under the curve; BS, Brier score; MFPCA, multivariate functional principal component analysis; mFACEs, multivariate fast covariance estimation.

4. Application to the ADNI study

The ADNI is a longitudinal study collecting neuroimaging data, biological and genetic markers, and clinical assessments to better measure the progression of AD. Currently, ADNI is on its third phase, ADNI 3, while previous phases include ADNI 1, Go, and 2. More information on the ADNI study can be found at their website (http://adni.loni.ucla.edu). In our study, we examine the combined subjects from all the previous phases of ADNI (ADNI 1, Go, and 2). In addition, we only included subjects without missing baseline measurements and had at least two observations for all longitudinal covariates. In total, 511 MCI patients met these criteria, of which 153 progressed to AD. Patients were typically reassessed at every six-month interval with an average number of visits of 8.11 (SD: 2.99, range: 2–21).

We focused on incorporating the results of longitudinal clinical assessments into our analysis. More specifically, we examined five important cognitive and functional assessments predictive of AD progression:⁵ the ADAS-Cog13 items, the Rey Auditory Verbal Learning Tests (immediate and learning scores), the Mini Mental State Examination, and the Functional Assessment Questionnaire. In addition, other available demographic variables, biomarkers, and imaging data collected at baseline which may be prognostic of AD progression were also included. The following demographic variables were included: baseline age, gender, years of education (Edu), marriage status (married/not married), race (white/other), ethnicity (Hispanic/non-Hispanic), and the presence of at least one apolipoprotein E allele (APOE4). In addition, the following baseline biomarker and imaging data were included: tau, ptau, and amyloid-beta proteins, total intracranial volume (TCV), hippocampal volume, whole brain volume, and glucose metabolism in the brain measured by FDG-PET.

Ten-fold cross-validation was applied to the ADNI data, and the risk was predicted for subjects in the test set of each fold. The predicted risk for all subjects was pooled together before calculating the AUC and BS. MFPCA and mFACEs were used to extract scores from the five longitudinal clinical assessments. Five principal components were chosen to account for 95% of the total variation present in the longitudinal outcomes. These scores were then included as covariates with the other demographic and baseline measurements in both the RSF and Cox models. The proportional hazards assumption for the baseline covariates were checked using Schoenfeld residuals (Figure S4). The residual plots did not show extreme non-linearity and the individual and global tests for non-zero slopes were not significant, which suggests that the proportional hazards assumption is reasonably satisfied.

Landmark times were chosen at t = [1, 2, 3] years. Survival predictions were made at Δt = [1, 2] years after each landmark time. In Table 3, the results are presented and summarized. These results show that RSF with either MFPCA or mFACEs performs better than Cox with higher AUC and smaller BS. Specifically, when Δt is fixed to be a smaller prediction interval (one year), RSF has comparable or better AUC than Cox at different landmark times. This continues to be the case when Δt is increased to two years. Furthermore, as the prediction interval is increased, the BS naturally increases as well. However, for all combinations of t and Δt’s, the BSs for RSF were lower than the BSs for Cox. These results suggest that the functional survival forests framework has better predictive performance in both discrimination and calibration when considering prediction windows of different lengths.

Table 3.

Comparison of RSF and Cox as survival submodels in the ADNI study.

		RSF		Cox
t	Δt	AUC	BS	AUC	BS
MFPCA
1	1	0.860	0.076	0.878	0.085
1	2	0.923	0.150	0.912	0.163
2	1	0.942	0.086	0.911	0.096
2	2	0.922	0.128	0.903	0.136
3	1	0.844	0.052	0.865	0.058
3	2	0.899	0.097	0.902	0.106
mFACEs
1	1	0.871	0.079	0.871	0.085
1	2	0.922	0.160	0.907	0.176
2	1	0.935	0.089	0.897	0.098
2	2	0.924	0.131	0.900	0.142
3	1	0.848	0.051	0.857	0.056
3	2	0.912	0.097	0.871	0.103

RSF, random survival forest; AUC, area under the curve; BS, Brier score; MFPCA, multivariate functional principal component analysis; mFACEs, multivariate fast covariance estimation.

An advantage of the functional survival forest is being able to update personalized predictions as new longitudinal data become available. We demonstrate how personalized dynamic predictions can be made for two individuals in the ADNI study using the MFPCA-RSF model built using all the data except for these two patients. The first patient is a 70-year-old male with one copy of the APOE4 gene. The second patient is an 82-year-old female with no copies of the APOE4 gene. The dynamic prediction setting and its corresponding predicted survival probabilities are displayed graphically in Figure 1. Here, each patient is examined in the time window of 0–7 years starting from enrollment. The patient survival is updated annually at each landmark time, starting from the first year and ending with the fourth. Predicted survival probabilities are made for the remainder of the seven years with survival curves plotted from the cubic spline smoothed trajectories. Although not investigated in the simulation study, we also provide the 95% confidence intervals for the survival probabilities which are calculated from 100 bootstrap samples of the data. As the landmark time increases, more follow-up measurements from the patients are included in the model leading to updated survival probabilities and narrower confidence intervals. Both patients have risk factors associated with AD. Patient A carries a copy of the APOE4 gene while patient B is female and more advanced in age. However, the predicted survival from Figure 1 shows that patient A is in relatively stable condition with narrow confidence intervals and low risk of disease progression. In comparison, patient B experiences a greater drop and higher uncertainty in event-free probability. These results suggest that patient B is at a higher risk for progressing to AD should be carefully monitored.

Figure 1.

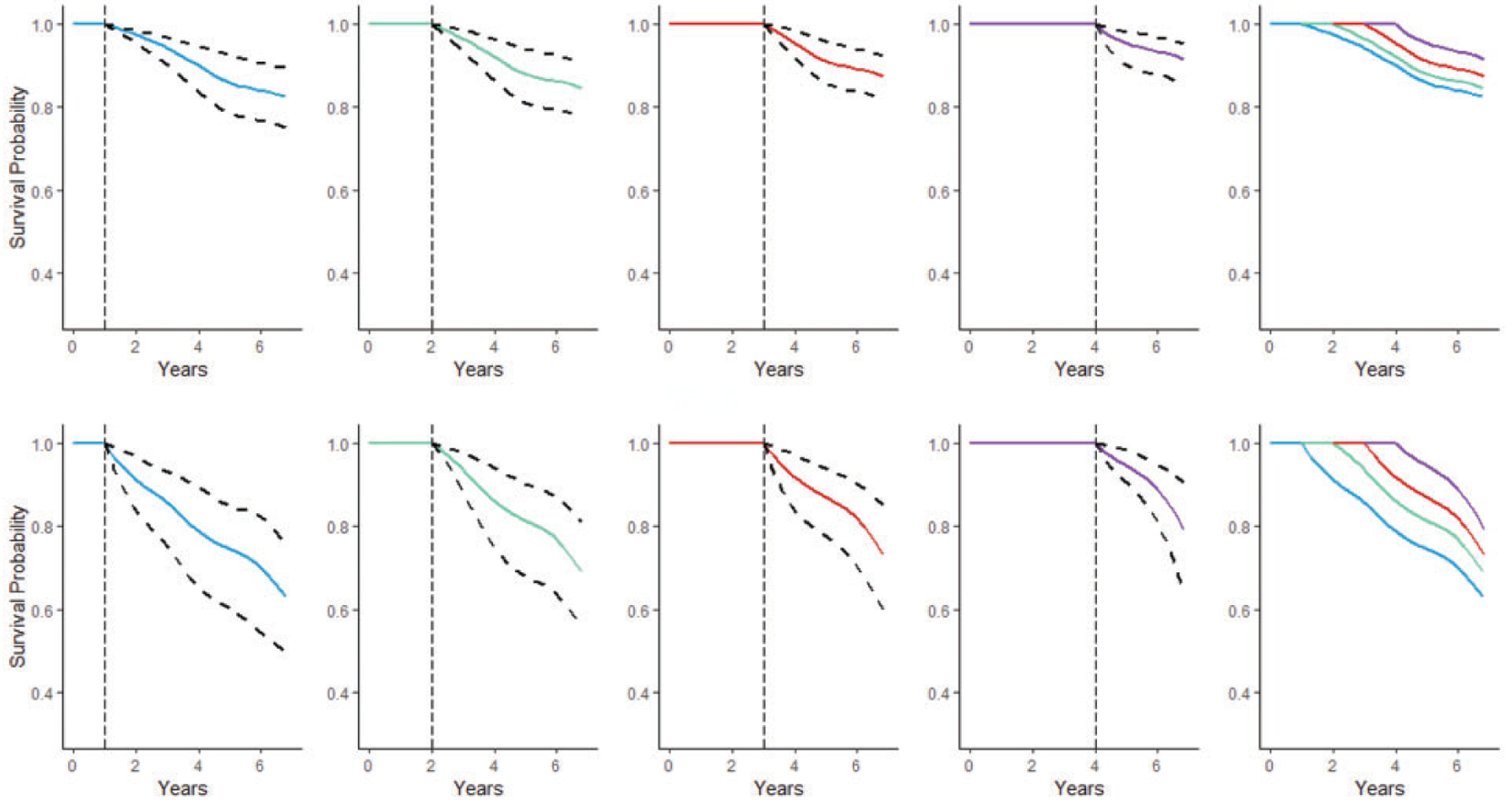
Dynamic progression-free probabilities with 95% bootstrap confidence intervals for patient A (upper panels) and patient B (lower panels). Landmark times are represented by vertical dashed lines. Survival curves are overlaid in the final column.

VIMP was also calculated for the MFPCA-RSF model built using all the ADNI data to assess the significance of each variable. Figure 2 displays the relative importance of the 10 most important variables ranked by VIMP. First, the longitudinal outcomes contribute highly to the performance of the model in predicting AD progression with the first principal component score (PVE = 0.826) having a large VIMP relative to other covariates. The scores of the second principal component (PVE = 0.119) and fifth principal component (PVE = 0.004) also important, ranking seventh and third, respectively. VIMP also identified several other key baseline variables derived from imaging scans and cerebrospinal fluid proteins. Of these variables, FDG-PET, which is used to visualize the level of glucose metabolism in the brain, was the most informative, as areas with hypometabolism are a strong indicator of neurodegeneration and cognitive decline.²⁵ Hippocampal volume was the only volumetric scan identified in this list, which agrees with studies showing that hippocampal volume is a more informative predictor of AD progression compared to whole brain volume.²⁶ Baseline levels of Amyloid-beta, Tau, and pTau proteins are also notable predictors.²⁷ The results from Figure 2 suggest that in addition to well documented baseline risk factors, the five longitudinal outcomes are strong predictors of AD diagnosis.

Figure 2.

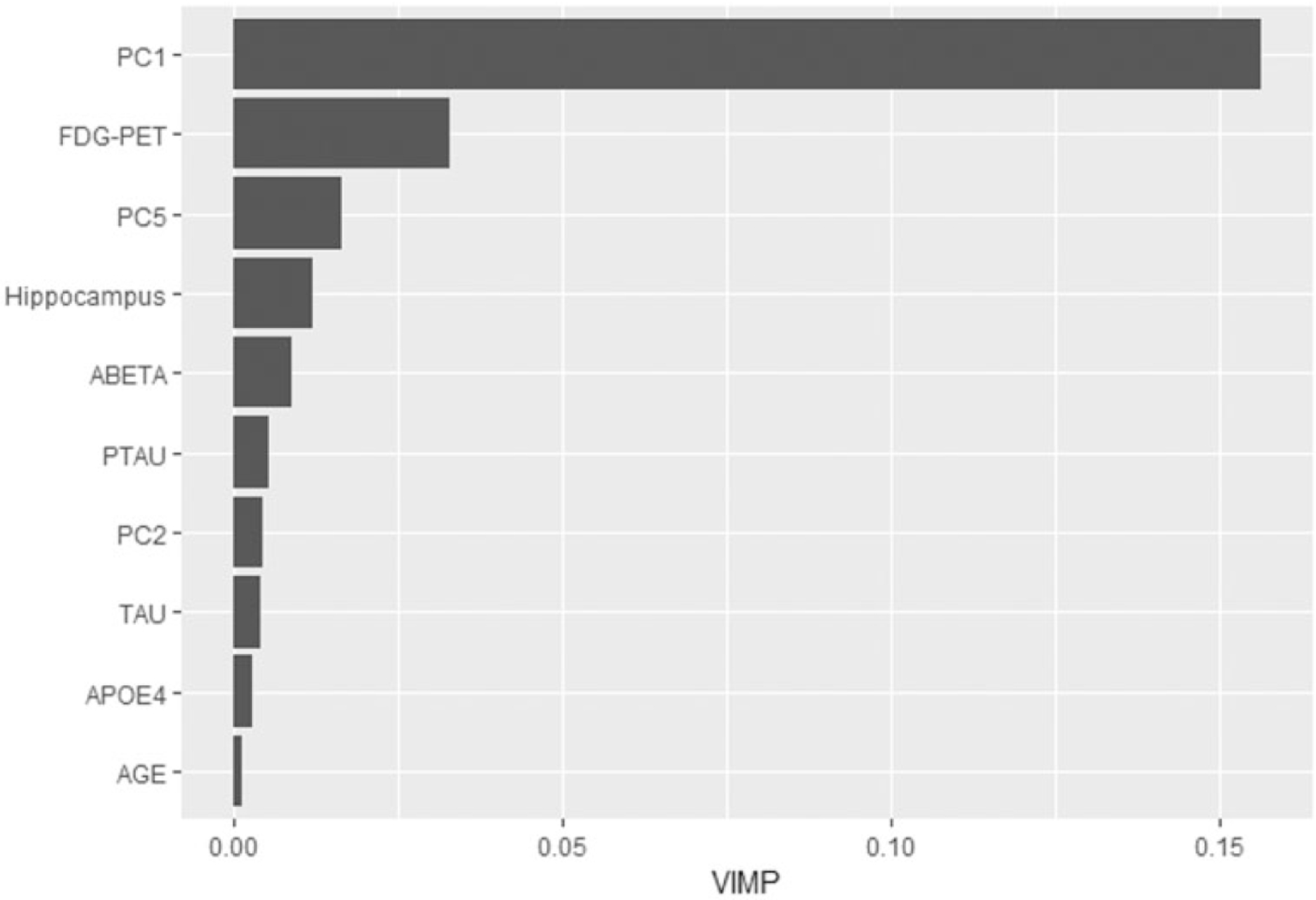
First 10 covariates ranked by variable importance: PC1, first principal component; FDG-PET, average FDG-PET of angular, temporal, and posterior cingulate at baseline; PC5, fifth principal component; Hippocampus, baseline hippocampus; ABETA, baseline Amyloid Beta; PTAU, baseline phosphorylated Tau protein; PC2, second principal component; TAU, baseline Tau protein; APOE4, apolipoprotein E4 allele; AGE, baseline age.

5. Discussion

We have developed a functional survival forests framework that is capable of incorporating longitudinal information. Multivariate functional principal component methods, MFPCA and mFACEs, were used to extract informative features from the trajectories of longitudinal outcomes. These methods are able to deal with both temporal correlation within patients’ repeated measures and correlation between different longitudinal outcomes. The resulting MFPC scores were then included as covariates in the RSF. Because RSF is non-parametric and makes no assumptions about the underlying distribution, it is more robust when considering scenarios with non-linear effects. Through simulation, RSF was shown to be able to handle cases where the model was not fully specified. Being able to identify interactions between variables without having to explicitly model them is often advantageous as the effects of these interactions are not always apparent. In addition, as the number of variables increases, it is not realistic to consider all possible interactions, which often leads to interactions being included subjectively or through stepwise selection. This flexibility allows RSF to have more robust discrimination and calibration metrics in dynamic prediction. Furthermore, both functional principal component methods, MFPCA and mFACEs, have performed well in extracting features. While Li et al.¹⁰ have suggested that mFACEs is better at reconstructing and predicting the longitudinal outcomes when the functional data are sparse, we did not detect a noticeable difference in dynamic prediction between mFACEs and MFPCA in the scenarios that we considered.

When applying our method to the ADNI dataset, the results suggested that the functional survival forest model is able to better identify patterns in the data, leading to higher predictive power for the progression of AD compared to its Cox counterpart. As such, RSF may hold an advantage over Cox as the dimensionality of the data increases, partially due to the potential for more noisy covariates being included, but also because more complex interactions between covariates may occur as well. The longitudinal outcomes play an important role in prediction as indicated by the higher rank of principal components in VIMP. We note that a limitation of applying VIMP to our method is the inability to assess the contribution of each individual longitudinal outcome to the high importance of the principal components. Despite this, VIMP still identified several other important baseline imaging and biomarker variables: FDG-PET, Hippocampus, ABeta, PTau, and Tau. While repeated measures of imaging and CSF markers are more scarce, capturing their longitudinal evolution rather than just their baseline values may provide valuable insight to AD progression.

Further improvements to the model may be achieved by automated tuning of parameters. RSF has a number of important parameters such as the number of predictors considered for each split and the number of cases in a terminal node which may vary the results depending on the parameter settings. In this article, the forest was built on the recommended default settings which are suggested to perform well in general.¹² However, Hastie et al.²⁸ also suggest that optimal values for these parameters differ depending on the problem and parameter tuning may result in better model performance.

Another consideration for RSF is the problem of interval censoring. Especially for longitudinal studies, patients often return for follow-up visits in regular intervals. Therefore, the true event time is only known to lie within an interval between visits and the exact time is obscured. Multiple studies have shown that ignoring interval censoring may lead to biased estimates for the survival outcome.^29,30 Methodology for modeling interval-censored data has been well developed for the Cox model.³⁰ While some ensemble-based methods such as the ICcforest³¹ and transformation forests³² have been adapted to address the issue of interval censoring, it is still an area of active research. As a future research direction, we will extend functional survival forests to account for interval censoring. Overall, we have demonstrated that RSF can be applied to discover more complex interactions and relationships between variables without further subjective input. When multivariate longitudinal outcomes are available, we advocate for the use of functional survival forests as an extension of RSF for improved model prediction.