Mathematical modeling of coronavirus disease COVID-19 dynamics using CF and ABC non-singular fractional derivatives

Abstract

In this article, Coronavirus Disease COVID-19 transmission dynamics were studied to examine the utility of the SEIR compartmental model, using two non-singular kernel fractional derivative operators. This method was used to evaluate the complete memory effects within the model. The Caputo–Fabrizio (CF) and Atangana–Baleanu models were used predicatively, to demonstrate the possible long–term trajectories of COVID-19. Thus, the expression of the basic reproduction number using the next generating matrix was derived. We also investigated the local stability of the equilibrium points. Additionally, we examined the existence and uniqueness of the solution for both extensions of these models. Comparisons of these two epidemic modeling approaches (i.e. CF and ABC fractional derivative) illustrated that, for non-integer $\tau$ value. The ABC approach had a significant effect on the dynamics of the epidemic and provided new perspective for its utilization as a tool to advance research in disease transmission dynamics for critical COVID-19 cases. Concurrently, the CF approach demonstrated promise for use in mild cases. Furthermore, the integer $\tau$ value results of both approaches were identical.

1. Introduction

Coronaviruses are a vast family of viruses, especially common in animals. Coronavirus was named for its corona or crown-like appearance under the microscope: the virus is surrounded by pointed structures. The severity of earlier coronavirus outbreaks can be evaluated by reflecting on the serious consequences of the SARS (Severe Acute Respiratory Syndrome) outbreak, which occured in 2003 [1]. Similarly, the MERS (Middle East Respiratory Syndrome) outbreak in 2012 [2] had widespread socioeconomic impacts as well. In December of 2019, a deadly respiratory viral infection appeared in the citizens of Wuhan, China. The virus was temporarily dubbed Novel Coronavirus 2019-nCoV. Then, on Feb 11, 2020, the virus was officially named by The World Health Organization (WHO) as Coronavirus Disease 2019 short form–COVID-19, caused by the virus SARS-CoV-2, which is 96% identical at the whole-genome level to the coronavirus found in bats [3], [4]. COVID-19 has an extremely high rate of transmission when compared to other coronaviruses such as SARS and MERS and other viruses such as HIV and Ebola. Beginning Jan 23, 2020, the Chinese government enacted strict measures for disease containment. This included a lockdown of Wuhan city to prevent the spread of this highly contagious disease. Finally, on Jan 30, 2020, the WHO declared the outbreak a global health emergency. Consequently, on March 11, 2020 the WHO declared COVID-19 a pandemic. Preliminary reports indicate 27 of 44 patients infected with COVID-19 had exposure to the Huanan seafood market in the city of Wuhan, in the Hubei province of China [5]. COVID-19 was transmitted from the animal to human population and is now communicable–spreading through human to human contact. However, the route of transmission into the human population, at the start of this event remains unclear. There is a long list of proposed studies on the origins of COVID-19. Human to human transmission can be caused by respiratory droplets and contact with infected individuals. Symptoms include fever, expectoration, headache, fatigue, dry cough, dyspnoea and organ failure in critical cases [6]. The incubation period as per the WHO ranges from 1–14 days. The WHO confirms over many regions and countries, a total of 70,476,836 laboratory-confirmed infections of COVID-19 including 1,599,922 deaths worldwide as of Dec 20, 2020 [7]. Laboratory-confirmed case data is considered the gold standard, due to the specificity of this diagnostic test: reverse transcription-polymerase chain reaction (RT-PCR) for COVID-19 [8]. Research is consistent in its findings, with human to human transmission of COVID-19 occurring mainly via symptomatic individuals. At present, with no effective treatment, the most effectual way to prevent transmission of the disease is to avoid infection. This can be accomplished through personal protective measures. Specific disease transmission mitigation efforts include isolation of all patients with flu-like symptoms, cluster investigations, proper mask wearing, avoiding close contact with people, and implementing strict hygiene measures [9].

In addition to all data mentioned above, Kilbas et al. [10] provides a brief theory and application of various fractional differential equations. Fractional calculus is used to study the dynamics of real-world problems in various fields of science. A recently published survey-cum-expository review article [11] provides an elementary and introductory overview of fractional calculus for nonprofessional readers. More specifically, the fields of engineering, epidemiology and social sciences have various mathematical modeling applications for mitigating public health risks [12], [13], [14], [15], [16], [17], [18]. In epidemiology, deterministic mathematical models have an important function in investigating the dynamics of infectious diseases. Very recently, Srivastava et al. [19], Srivastava and Saad [20] investigated fractional calculus and fractal-fractional calculus applications in modeling the dynamics of the Ebola virus with three different kernels using numerical simulations; also we can see the fractional models of Diabetes in [21]. Whereas, a comparative study of the fractional clock chemical model’s numerical results (with a finding of an exact result) was carried out in [22]. Recently published articles have been formulated on the transmission dynamics of COVID-19. However, current research is mainly restricted to classical integer-order models, logistic models and delay or stochastic differential equation models  [23], [24], [25], [26], [27], [28], [29], [30]. Recently, the Atangana–Baleanu fractional derivative was applied in order to create a mathematical model for the dynamics of the novel corona virus in [31] and pointed out the need for evaluating the comparison with other derivative operators.

Often, in epidemiological analysis, diseases caused by viruses grow exponentially with a fixed reproduction rate. Similarly, the growth curve for the number of COVID-19 diagnoses outside China are exponential, as demonstrated by Li et al. [32], Lau and Khosrawipour [33]. The following research [34] supports the likelihood that due to various prevention measures, growth decreased exponentially. Until present, research has not yet explored comparisons of the CF and ABC fractional derivative operators against the transmission dynamics of the COVID-19 SEIR model, which has non-singular kernels, the memory effects, crossover properties and other important properties when compared to the integer order derivative. The findings above make the CF fractional derivative and ABC fractional derivative promising options for use as a mathematical tool in modeling the transmission dynamics of COVID-19.

In the following sections, the COVID-19 SEIR standard incidence compartmental ODE model is extended to the fractional differential equation model. This is accomplished by using two different non-singular kernel fractional derivatives, both CF and ABC fractional derivative operators. This approach is used to study the trajectory of transmission of infection. The expression for the basic reproduction number (using the next generating matrix method) is derived and local stability of the equilibrium points are analyzed. The existence and uniqueness of both COVID-19 fractional models are proved via the fixed-point theorem. We also analyze the changing trends of the COVID-19 pandemic with graphs for numerical simulations of both CF and ABC approach models. Considering the timeline for disease onset to clinical recovery and severity of illness, we discuss the suitability of using both operators, accompanied by relative similarities, as well as their differences. Lastly, we conclude the article by analyzing the importance of disease transmission models and discuss their future implications for disease control policy development at both national and International levels to interrupt or minimize transmission chains in humans.

2. Definitions of the non-singular fractional order derivatives

In this section, we present the basic definitions of the new fractional derivatives with exponential and Mittag-Leffler kernels.

Definition 1

Consider ${\rm Y}\in H^1(b_1,b_2),$ $b_2>b_1,$ $\tau \in [0,1],$ then the Caputo-Fabrizio (CF) fractional derivative is defined as [35]:

$${}_{b1}^{CF}{D}_t^{\tau }\left[{\rm Y}\left(t\right)\right]=\frac{\mathcal{F}\left(\tau \right)}{1-\tau }{\int }_{b_1}^t{{\rm Y}}^{\prime }\left(x\right)\exp [-\tau \frac{t-x}{1-\tau }]dx,$$ (1)

where $\mathcal{F}\left(\tau \right)$ is a normalization function satisfying $\mathcal{F}\left(0\right)=\mathcal{F}\left(1\right)=1$ if ${\rm Y}\notin H^1(b_1,b_2)$ then

$$D_t^{\tau }\left({\rm Y}\left(t\right)\right)=\frac{\tau \mathcal{F}\left(\tau \right)}{1-\tau }{\int }_{b_1}^t({\rm Y}\left(t\right)-{\rm Y}\left(x\right))\exp [-\tau \frac{t-x}{1-\tau }]dx.$$ (2)

Definition 2

Let $0<\tau <1,$ then the integral of the fractional order $\tau$ for a function ${\rm Y}\left(t\right)$ is defined as [35], [36]:

$$I_t^{\tau }\left({\rm Y}\left(t\right)\right)=\frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}{\rm Y}\left(t\right)+\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\int }_0^t{\rm Y}\left(s\right)ds,t\ge 0.$$ (3)

Definition 3

Consider ${\rm Y}\in H^1(b_1,b_2),$ $b_2>b_1,$ $\tau \in [0,1],$ then the Atangana-Baleanu derivative in the Caputo sense (ABC) is defined as [37]:

$${}_{b1}^{ABC}{D}_t^{\tau }\left[{\rm Y}\left(t\right)\right]=\frac{\mathcal{B}\left(\tau \right)}{1-\tau }{\int }_{b_1}^t{{\rm Y}}^{\prime }\left(x\right)E_{\tau }[-\tau \frac{{(t-x)}^{\tau }}{1-\tau }]dx,$$ (4)

where $E_{\tau }$ represent the Mittag-Leffler function and $\mathcal{B}\left(\tau \right)$ is a normalization function satisfying $\mathcal{B}\left(0\right)=\mathcal{B}\left(1\right)=1$ and $\mathcal{B}\left(\tau \right)=1-\tau +\frac{\tau }{\Gamma \left(\tau \right)}$.

Definition 4

[37] Let $0<\tau <1,$ then the integral of the Atangana-Baleanu derivative in the Caputo sense, fractional order $\tau$ for a function ${\rm Y}\left(t\right)$ is defined as:

$$\begin{array}{ccc}\hfill {}_{b1}^{ABC}{I}_t^{\tau }\left[{\rm Y}\left(t\right)\right]& =& \frac{1-\tau }{\mathcal{B}\left(\tau \right)}{\rm Y}\left(t\right)+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}\hfill \\ & & \times {\int }_{b1}^t{(t-s)}^{\tau -1}{\rm Y}\left(s\right)ds,t\ge 0.\hfill \end{array}$$ (5)

3. Model formulation of COVID-19

Considering the transmission method is human to human, we chose a model for the transmission dynamics of COVID-19 based on the SEIR compartmental model (susceptible exposed infected recovery model) with standard incidence [38]. Assuming all individuals are susceptible, and that infected individuals can spread the disease, this model was represented via the nonlinear system below.

$$\begin{array}{ccc}\hfill S^{\prime }\left(t\right)& =& \Pi -\frac{\beta S\left(t\right)I\left(t\right)}{N}-mS\left(t\right),\hfill \\ \hfill E^{\prime }\left(t\right)& =& \frac{\beta S\left(t\right)I\left(t\right)}{N}-(m+\psi )E\left(t\right),\hfill \\ \hfill I^{\prime }\left(t\right)& =& \psi E\left(t\right)-(m+\gamma )I\left(t\right),\hfill \\ \hfill R^{\prime }\left(t\right)& =& \gamma I\left(t\right)-mR\left(t\right).\hfill \end{array}$$ (6)

The equations above created four compartments, for a total number of individuals labelled at time $t$. As such, these were categorized as ($S\left(t\right)$) susceptible individuals whom were not considered infected but as having the capacity to become infected, $\left(E\right(t\left)\right)$ exposed individuals are those who have been infected but are not infectious, $\left(I\right(t\left)\right)$ infectious individuals are those who are symptomatic and clinically tested. Lastly, $\left(R\right(t\left)\right)$ removed individuals are those who have recovered from the disease. The total population was denoted by $N$ such that $N=S\left(t\right)+E\left(t\right)+I\left(t\right)+R\left(t\right)$ was considered constant with an assumption of birth rate represented as $n,$ and death rate as $m$. All parameters were positive constants described as $(\Pi =nN)$ rate of recruitment of individuals, $\left(\beta \right)$ transmission rate of the disease upon contact with symptomatic infected individuals. Moreover, the parameter $\left({\psi }^{-1}\right)$ represented the latency period of 3 to 5 days and $\left({\gamma }^{-1}\right)$ represented the infectious period within the range of 2 to 14 days [39].

The ODE model for COVID-19 was extended to the fractional order model using the CF derivative below:

$$\begin{array}{ccc}\hfill {}_0^{CF}{D}_t^{\tau }S\left(t\right)& =& \Pi -\frac{\beta S\left(t\right)I\left(t\right)}{N}-mS\left(t\right),\hfill \\ \hfill {}_0^{CF}{D}_t^{\tau }E\left(t\right)& =& \frac{\beta S\left(t\right)I\left(t\right)}{N}-(m+\psi )E\left(t\right),\hfill \\ \hfill {}_0^{CF}{D}_t^{\tau }I\left(t\right)& =& \psi E\left(t\right)-(m+\gamma )I\left(t\right),\hfill \\ \hfill {}_0^{CF}{D}_t^{\tau }R\left(t\right)& =& \gamma I\left(t\right)-mR\left(t\right).\hfill \end{array}$$ (7)

Similarly, the ODE model for COVID-19 was extended to the fractional order model with Atangana-Baleanu in the Caputo sense (ABC) fractional derivative provided below:

$$\begin{array}{ccc}\hfill {}_0^{ABC}{D}_t^{\tau }S\left(t\right)& =& \Pi -\frac{\beta S\left(t\right)I\left(t\right)}{N}-mS\left(t\right),\hfill \\ \hfill {}_0^{ABC}{D}_t^{\tau }E\left(t\right)& =& \frac{\beta S\left(t\right)I\left(t\right)}{N}-(m+\psi )E\left(t\right),\hfill \\ \hfill {}_0^{ABC}{D}_t^{\tau }I\left(t\right)& =& \psi E\left(t\right)-(m+\gamma )I\left(t\right),\hfill \\ \hfill {}_0^{ABC}{D}_t^{\tau }R\left(t\right)& =& \gamma I\left(t\right)-mR\left(t\right).\hfill \end{array}$$ (8)

The initial conditions involved throughout the analysis were

$$S\left(0\right)=S_0\ge 0,E\left(0\right)=E_0\ge 0,I\left(0\right)=I_0\ge 0,andR\left(0\right)=R_0\ge 0.$$ (9)

3.1. Equilibria and basic reproduction number

Reproduction number is a crucial figure within the mathematical analysis of any disease model:- it aids in determining if an epidemic will likely occur. The reproduction number ${\mathcal{R}}_0$ of the model represents the anticipated sum of infectious cases generated by one infectious individual within a population of susceptible individuals. The value of ${\mathcal{R}}_0$ for the aforementioned models, utilized the next-generation matrix method given by Driessche and Watmough [40]. Findings indicated the relevant Jacobian matrices F and V were associated with the rate of appearance of new infections and with net rate out of the corresponding compartments, respectively were given by

$$\begin{array}{c}\hfill F=\left(\begin{array}{cc}0& \beta \\ 0& 0\end{array}\right),V=\left(\begin{array}{cc}m+\psi & 0\\ -\psi & m+\gamma \end{array}\right).\end{array}$$ (10)

Thus, we find

$$\begin{array}{c}\hfill F{V}^{-1}=\left(\begin{array}{cc}\frac{\beta \psi }{(m+\psi )(m+\gamma )}& \frac{\beta }{m+\gamma }\\ 0& 0\end{array}\right)=B.\end{array}$$ (11)

solving for eigen values of B we find,

$${\lambda }_1=\frac{\beta \psi }{(m+\psi )(m+\gamma )}and{\lambda }_2=0.$$ (12)

The reproduction number ${\mathcal{R}}_0$ is given by the dominant eigenvalue. precisely,

$${\mathcal{R}}_0=\frac{\psi \beta }{(m+\psi )(m+\gamma )}.$$ (13)

If ${\mathcal{R}}_0<1$ then the disease would likely self-terminate. However, if ${\mathcal{R}}_0>1$ then the disease would likely prevail and become a pandemic if containment procedures are not initiated.

We found two biologically meaningful equilibria. One was disease-free equilibrium ${\mathcal{T}}_0$ and an endemic equilibrium (EE)${\mathcal{T}}_1$.

The disease-free equilibrium (DFE) ${\mathcal{T}}_0$ of the system (7), (8) was found by taking zero value for the derivatives side, considering there are no exposed individuals.

Thus, by substitution in the aforementioned systems we found,

$${\mathcal{T}}_0=(S^0,0,0,0)=(\frac{\Pi }{m},0,0,0).$$ (14)

The endemic equilibrium points ${\mathcal{T}}_1$ were derived by considering a population of infected individuals and all equations of models (7), (8) are equal to zero. Effectively denoted in-terms of ${\mathcal{R}}_0$ as

$$\begin{array}{ccc}\hfill S^{\circ }& =& \frac{N}{{\mathcal{R}}_0};E^{\circ }=\frac{mN(m+\gamma )({\mathcal{R}}_0-1)}{\beta \psi };\hfill \\ \hfill I^{\circ }& =& \frac{mN({\mathcal{R}}_0-1)}{\beta };R^{\circ }=\frac{\gamma N({\mathcal{R}}_0-1)}{\beta }.\hfill \end{array}$$ (15)

3.2. Local stability analysis in terms of the basic reproduction number

In this subsection we worked on the stability analysis of the COVID-19 model ((7), (8)).

Theorem 1

The DFE${\mathcal{T}}_0$of the COVID-19 model (7,8) was locally asymptotically stable if and only if${\mathcal{R}}_0<1$.

Proof

For the proof, we obtained at DFE ${\mathcal{T}}_0,$ the Jacobian matrix below,

$$\begin{array}{c}\hfill J\left({\mathcal{T}}_0\right)=\left(\begin{array}{cccc}-m& 0& -\beta & 0\\ 0& -(m+\psi )& \beta & 0\\ 0& \psi & -(m+\gamma )& 0\\ 0& 0& \gamma & -m\end{array}\right).\end{array}$$ (16)

The characteristic equation for the Jacobian matrix mentioned above is the form:

$$B\left(\lambda \right)=-{(\lambda +m)}^{2}P\left(\lambda \right)=0,$$ (17)

$$\begin{array}{ccc}\hfill P\left(\lambda \right)& =& {\lambda }^2+\lambda \left((m+\psi )(m+\gamma )\right)\hfill \\ & & +(1-{\mathcal{R}}_0)(m+\gamma )(m+\psi )]=0.\hfill \end{array}$$ (18)

For ${\mathcal{R}}_0<1$ the $P\left(\lambda \right)$ equation has all positive coefficients and by the criteria of Routh-Hurwitz for the second order polynomial $a_i>0$ for $i=0,1,2$. The DFE ${\mathcal{T}}_0$ of the COVID-19 model ((7), (8)) is locally asymptotically stable for ${\mathcal{R}}_0<1$. □

Theorem 2

The EE${\mathcal{T}}_1$of the COVID-19 model (7,8) is locally asymptotically stable for${\mathcal{R}}_0>1$and unstable for${\mathcal{R}}_0<1$.

Proof

For the proof, we obtain at EE ${\mathcal{T}}_1,$ the Jacobian matrix below,

$$\begin{array}{c}\hfill J\left({\mathcal{T}}_1\right)=\left(\begin{array}{cccc}-\frac{\beta I^{\circ }}{N}-m& 0& -\frac{\beta S^{\circ }}{N}& 0\\ \frac{\beta I^{\circ }}{N}& -(m+\psi )& \frac{\beta S^{\circ }}{N}& 0\\ 0& \psi & -(m+\gamma )& 0\\ 0& 0& \gamma & -m\end{array}\right).\end{array}$$ (19)

The characteristic equation for the Jacobian matrix mentioned above is the form:

$$C\left(\lambda \right)=-{(\lambda +m)}^{2}D\left(\lambda \right)=0,$$ (20)

$$D\left(\lambda \right)={\lambda }^3+a_1{\lambda }^2+a_2\lambda +a_3=0,$$ (21)

where,

$$a_1=(2m+\psi +\gamma )+m{\mathcal{R}}_0.$$ (22)

$$a_2=m(2m+\psi +\gamma ){\mathcal{R}}_0.$$ (23)

$$a_3=\frac{\beta \psi m}{{\mathcal{R}}_0}({\mathcal{R}}_0-1).$$ (24)

It is clearly shown that for ${\mathcal{R}}_0>1$ the above equation has all positive coefficients by the criteria of Routh-Hurwitz for the third order polynomial $a_1{a}_2>a_3$ for $i=0,1,2,3$. The EE ${\mathcal{T}}_1$ of the COVID-19 model ((7), (8)) is locally asymptotically stable for ${\mathcal{R}}_0>1$ and unstable for ${\mathcal{R}}_0<1$. □

4. Existence and uniqueness of COVID-19 model of fractional order with CF derivative

In this article, we have taken a nonlinear fractional order model into consideration. The following section focuses on investigation of both the existence and uniqueness of the solution concerning the aforementioned model (7) by applying the fixed-point theory.

The CF model is represented by Eq. (7) in applying the fractional integral [36], our findings include the following;

$$\begin{array}{ccc}\hfill S\left(t\right)-S\left(0\right)& =& {}_0^{CF}{I}_t^{\tau }\{\Pi -\frac{\beta S\left(t\right)I\left(t\right)}{N}-mS\left(t\right)\},\hfill \\ \hfill E\left(t\right)-E\left(0\right)& =& {}_0^{CF}{I}_t^{\tau }\{\frac{\beta S\left(t\right)I\left(t\right)}{N}-(m+\psi )E\left(t\right)\},\hfill \\ \hfill I\left(t\right)-I\left(0\right)& =& {}_0^{CF}{I}_t^{\tau }\{\psi E\left(t\right)-(m+\gamma )I\left(t\right)\},\hfill \\ \hfill R\left(t\right)-R\left(0\right)& =& {}_0^{CF}{I}_t^{\tau }\{\gamma I\left(t\right)-mR\left(t\right)\}.\hfill \end{array}$$ (25)

The notations [36], when organized within the context of the problem yield the following results;

$$\begin{array}{ccc}\hfill S\left(t\right)-S\left(0\right)& =& \frac{2(1-\tau )}{\mathcal{F}\left(\tau \right)(2-\tau )}\{\Pi -\frac{\beta S\left(t\right)I\left(t\right)}{N}-mS\left(t\right)\}+\frac{2\tau }{\mathcal{F}\left(\tau \right)(2-\tau )}{\int }_0^t\{\Pi -\frac{\beta S\left(\zeta \right)I\left(\zeta \right)}{N}-mS\left(\zeta \right)\left)\right\}d\zeta ,\hfill \\ \hfill E\left(t\right)-E\left(0\right)& =& \frac{2(1-\tau )}{\mathcal{F}\left(\tau \right)(2-\tau )}\{\frac{\beta S\left(t\right)I\left(t\right)}{N}-(m+\psi )E\left(t\right)\}+\frac{2\tau }{\mathcal{F}\left(\tau \right)(2-\tau )}{\int }_0^t\{\frac{\beta S\left(\zeta \right)I\left(\zeta \right)}{N}-(m+\psi )E\left(\zeta \right)\}d\zeta ,\hfill \\ \hfill I\left(t\right)-I\left(0\right)& =& \frac{2(1-\tau )}{\mathcal{F}\left(\tau \right)(2-\tau )}\{\psi E\left(t\right)-(m+\gamma )I\left(t\right)\}+\frac{2\tau }{\mathcal{F}\left(\tau \right)(2-\tau )}{\int }_0^t\{\psi E\left(\zeta \right)-(m+\gamma )I\left(\zeta \right)\}d\zeta ,\hfill \\ \hfill R\left(t\right)-R\left(0\right)& =& \frac{2(1-\tau )}{\mathcal{F}\left(\tau \right)(2-\tau )}\{\gamma I\left(t\right)-mR\left(t\right)\}+\frac{2\tau }{\mathcal{F}\left(\tau \right)(2-\tau )}{\int }_0^t\{\gamma I\left(\zeta \right)-mR\left(\zeta \right)\}d\zeta .\hfill \end{array}$$ (26)

We interpret for clarity;

$$\begin{array}{ccc}\hfill C_1(t,S)& =& \Pi -\frac{\beta S\left(t\right)I\left(t\right)}{N}-mS\left(t\right),\hfill \\ \hfill C_2(t,E)& =& \frac{\beta S\left(t\right)I\left(t\right)}{N}-(m+\psi )E\left(t\right),\hfill \\ \hfill C_3(t,A)& =& \psi E\left(t\right)-(m+\gamma )I\left(t\right),\hfill \\ \hfill C_4(t,C)& =& \gamma I\left(t\right)-mR\left(t\right).\hfill \end{array}$$ (27)

Theorem 3

If the inequality given below holds

$$0\le \left(\frac{\beta a}{N}+m\right)<1,$$

then, the kernel $C_1$ justifies the Lipschitz condition and contraction.

Proof

Assume $S$ and $S_1$ are two functions, with that we have

$$\parallel C_1(t,S)-C_1(t,S_1)\parallel =\left|\right|-\frac{\beta (S\left(t\right)-S\left(t_1\right))I\left(t\right)}{N}-m(S\left(t\right)-S\left(t_1\right))\left|\right|.$$ (28)

Applying the triangular inequality on Eq. (28) gives

$$\begin{array}{ccc}\hfill \parallel C_1(t,S)-C_1(t,S_1)\parallel & \le & \left|\right|\frac{\beta I\left(t\right)(S\left(t\right)-S\left(t_1\right))}{N}\left|\right|+\parallel m(S\left(t\right)-S\left(t_1\right))\parallel ,\hfill \\ & \le & [\frac{\beta \parallel I\left(t\right)\parallel }{N}+m]\parallel (S\left(t\right)-S\left(t_1\right))\parallel ,\hfill \\ & \le & \left[\frac{\beta a}{N}+m\right]\parallel S\left(t\right)-S\left(t_1\right)\parallel ,\hfill \\ & \le & {\theta }_1\parallel \{S\left(t\right)-S\left(t_1\right)\}\parallel .\hfill \end{array}$$ (29)

Let ${\theta }_1=\frac{\beta a}{N}+m,$ where $\parallel S\left(t\right)\parallel \le s,$ $\parallel R\left(t\right)\parallel \le r$, $\parallel I\left(t\right)\parallel \le a$ and $\parallel E\left(t\right)\parallel \le b$ are bounded functions, we get

$$\parallel C_1(t,S)-C_1(t,S_1)\parallel \le {\theta }_1\parallel S\left(t\right)-S\left(t_1\right)\parallel .$$ (30)

Hence, the Lipschitz condition is obtained for kernel $C_1$ and $0\le \left(\frac{\beta a}{N}+m\right)<1$ provides $C_1,$ which satisfies contraction.

Similarly, for the other kernels the Lipschitz condition and contraction can be performed and written as shown;

$$\begin{array}{ccc}\hfill \parallel C_2(t,E)-C_2(t,E_1)\parallel & \le & {\theta }_2\parallel E\left(t\right)-E\left(t_1\right)\parallel ,\hfill \\ \hfill \parallel C_3(t,I)-C_2(t,I_1)\parallel & \le & {\theta }_3\parallel I\left(t\right)-I\left(t_1\right)\parallel ,\hfill \\ \hfill \parallel C_4(t,R)-C_2(t,R_1)\parallel & \le & {\theta }_4\parallel R\left(t\right)-R\left(t_1\right)\parallel .\hfill \end{array}$$ (31)

Taking the aforementioned kernels Eq. (26) becomes

$$\begin{array}{ccc}\hfill S\left(t\right)& =& S\left(0\right)+\frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}{C}_1(t,S)+\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\int }_0^t\left(C_1(\zeta ,S)\right)d\zeta ,\hfill \\ \hfill E\left(t\right)& =& E\left(0\right)+\frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}{C}_2(t,E)+\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\int }_0^t\left(C_2(\zeta ,E)\right)d\zeta ,\hfill \\ \hfill I\left(t\right)& =& I\left(0\right)+\frac{2(1-\tau )}{\mathcal{F}\left(\tau \right)(2-\tau )}{C}_3(t,I)+\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\int }_0^t\left(C_3(\zeta ,I)\right)d\zeta ,\hfill \\ \hfill R\left(t\right)& =& R\left(0\right)+\frac{2(1-\tau )}{\mathcal{F}\left(\tau \right)(2-\tau )}{C}_4(t,R)+\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\int }_0^t\left(C_4(\zeta ,R)\right)d\zeta .\hfill \end{array}$$ (32)

We focus on the following recursive formulae, given as

$$\begin{array}{ccc}\hfill S_n\left(t\right)& =& \frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}{C}_1(t,S_{n-1})+\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\int }_0^t\left(C_1(\zeta ,S_{n-1})\right)d\zeta ,\hfill \\ \hfill E_n\left(t\right)& =& \frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}{C}_2(t,E_{n-1})+\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\int }_0^t\left(C_2(\zeta ,E_{n-1})\right)d\zeta ,\hfill \\ \hfill I_n\left(t\right)& =& \frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}{C}_3(t,I_{n-1})+\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\int }_0^t\left(C_3(\zeta ,I_{n-1})\right)d\zeta ,\hfill \\ \hfill R_n\left(t\right)& =& \frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}{C}_4(t,R_{n-1})+\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\int }_0^t\left(C_4(\zeta ,R_{n-1})\right)d\zeta .\hfill \end{array}$$ (33)

Along with

$$S_0\left(t\right)=S\left(0\right),E_0\left(t\right)=E\left(0\right),I_0\left(t\right)=I\left(0\right),R_0\left(t\right)=R\left(0\right).$$ (34)

the initial conditions. The subsequent expressions for the difference of successive terms are expressed as:

$$\begin{array}{ccc}\hfill {\lambda }_n\left(t\right)& =& S_n\left(t\right)-S_{n-1}\left(t\right)=\frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}(C_1(t,S_{n-1})-C_1(t,S_{n-2}))+\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\int }_0^t(C_1(\zeta ,S_{n-1})-C_1(\zeta ,S_{n-2}))d\zeta ,\hfill \\ \hfill {\omega }_n\left(t\right))& =& E_n\left(t\right)-E_{n-1}\left(t\right)=\frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}(C_2(t,E_{n-1})-C_2(t,E_{n-2}))+\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\int }_0^t(C_2(\zeta ,E_{n-1})-C_2(\zeta ,E_{n-2}))d\zeta ,\hfill \\ \hfill {\xi }_n\left(t\right)& =& I_n\left(t\right)-I_{n-1}\left(t\right)=\frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}(C_3(t,I_{n-1})-C_3(t,I_{n-2}))+\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\int }_0^t(C_3(\zeta ,I_{n-1})-C_3(\zeta ,I_{n-2}))d\zeta ,\hfill \\ \hfill {\eta }_n\left(t\right)& =& R_n\left(t\right)-R_{n-1}\left(t\right)=\frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}(C_4(t,R_{n-1})-C_4(t,R_{n-2}))+\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\int }_0^t(C_4(\zeta ,R_{n-1})-C_4(\zeta ,R_{n-2}))d\zeta .\hfill \end{array}$$ (35)

It is obvious that

$$\begin{array}{c}\hfill \{\begin{array}{c}{S}_n\left(t\right)=\sum _{i=1}^n{\omega }_i\left(t\right),\hfill \\ \\ E_n\left(t\right)=\sum _{i=1}^n{\lambda }_i\left(t\right),\hfill \\ \\ I_n\left(t\right)=\sum _{i=1}^n{\xi }_i\left(t\right),\hfill \\ \\ R_n\left(t\right)=\sum _{i=1}^n{\eta }_i\left(t\right).\hfill \end{array}\end{array}$$ (36)

Applying the norm on Eq. (35), yields;

$$\parallel {\lambda }_n\left(t\right)\parallel =\parallel S_n\left(t\right)-S_{n-1}\left(t\right)\parallel =\left|\right|\frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}(C_1(t,S_{n-1})-C_1(t,S_{n-2}))+\frac{2\tau }{\mathcal{F}\left(\tau \right)(2-\tau )}{\int }_0^t(C_1(\zeta ,S_{n-1})-C_1(\zeta ,S_{n-2}))d\zeta \left|\right|.$$ (37)

Applying the triangular inequality, Eq. (37) reduces to

$$\parallel S_n\left(t\right)-S_{n-1}\left(t\right)\parallel \le \frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}\left|\right|(C_1(t,S_{n-1})-C_1(t,S_{n-2}))\left|\right|+\frac{2\tau }{\mathcal{F}\left(\tau \right)(2-\tau )}\left|\right|{\int }_0^t(C_1(\zeta ,S_{n-1})-C_1(\zeta ,S_{n-2}))d\zeta \left|\right|.$$ (38)

Since, the kernel $C_1$ satisfies the Lipschitz condition, we have

$$\parallel S_n\left(t\right)-S_{n-1}\left(t\right)\parallel \le \frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}{\theta }_1\parallel S_{n-1}-S_{n-2}\parallel +\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\theta }_1{\int }_0^t\parallel S_{n-1}-S_{n-2}\parallel d\zeta .$$ (39)

Therefore, we conclude;

$$\parallel {\lambda }_n\left(t\right)\parallel \le \frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}{\theta }_1\parallel {\lambda }_{n-1}\left(t\right)\parallel +\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\theta }_1{\int }_0^t\parallel {\lambda }_{n-1}\left(\zeta \right)\parallel d\zeta .$$ (40)

Similarly, we gain the following results

$$\begin{array}{ccc}\hfill \parallel {\omega }_n\left(t\right))\parallel & \le & \frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}{\theta }_2\parallel {\omega }_{n-1}\left(t\right)\parallel +\frac{2\tau }{\mathcal{F}\left(\tau \right)(2-\tau )}{\theta }_2{\int }_0^t\parallel {\omega }_{n-1}\left(\zeta \right)\parallel d\zeta ,\hfill \\ \hfill \parallel {\xi }_n\left(t\right)\parallel & \le & \frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}{\theta }_3\parallel {\xi }_{n-1}\left(t\right)\parallel +\frac{2\tau }{\mathcal{F}\left(\tau \right)(2-\tau )}{\theta }_3{\int }_0^t\parallel {\xi }_{n-1}\left(\zeta \right)\parallel d\zeta ,\hfill \\ \hfill \parallel {\eta }_n\left(t\right)\parallel & \le & \frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}{\theta }_4\parallel {\eta }_{n-1}\left(t\right)\parallel +\frac{2\tau }{\mathcal{F}\left(\tau \right)(2-\tau )}{\theta }_4{\int }_0^t\parallel {\eta }_{n-1}\left(\zeta \right)\parallel d\zeta .\hfill \end{array}$$ (41)

 □

Considering the above results, we present the following theorem:

Theorem 4

The COVID-19 fractional model(7)has a solutions if we can find a$t_0,$such that:

$$\frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}{\theta }_1+\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\theta }_1{t}_0<1.$$

Proof

Considering Eqs. (40) and (41), along with the fact that functions $S\left(t\right),$ $E\left(t\right),$ $I\left(t\right)$ and $R\left(t\right)$ are bounded and the kernels justify the Lipschitz condition. We have the following relation employing the recursive method:

$$\begin{array}{ccc}\hfill \parallel {\lambda }_n\left(t\right)\parallel & \le & \parallel S_n\left(0\right)\parallel \left[\right(\frac{2(1-\tau )}{\mathcal{F}\left(\tau \right)(2-\tau )}{\theta }_1)+(\frac{2\tau }{\mathcal{F}\left(\tau \right)(2-\tau )}{\theta }_{1}t\left)\right]{}^n,\hfill \\ \hfill \parallel {\omega }_n\left(t\right))\parallel & \le & \parallel E_n\left(0\right)\parallel \left[\right(\frac{2(1-\tau )}{\mathcal{F}\left(\tau \right)(2-\tau )}{\theta }_2)+(\frac{2\tau }{\mathcal{F}\left(\tau \right)(2-\tau )}{\theta }_{2}t\left)\right]{}^n,\hfill \\ \hfill \parallel {\xi }_n\left(t\right)\parallel & \le & \parallel A_n\left(0\right)\parallel \left[\right(\frac{2(1-\tau )}{\mathcal{F}\left(\tau \right)(2-\tau )}{\theta }_3)+(\frac{2\tau }{\mathcal{F}\left(\tau \right)(2-\tau )}{\theta }_{3}t\left)\right]{}^n,\hfill \\ \hfill \parallel {\eta }_n\left(t\right)\parallel & \le & \parallel C_n\left(0\right)\parallel \left[\right(\frac{2(1-\tau )}{2\mathcal{F}\left(\tau \right)-\tau \mathcal{F}\left(\tau \right)}{\theta }_4)+(\frac{2\tau }{\mathcal{F}\left(\tau \right)(2-\tau )}{\theta }_{4}t\left)\right]{}^n.\hfill \end{array}$$ (42)

Thus, we demonstrate solutions exist and also satisfy continuity, for the COVID-19 model (7). For the sake of clarity, the above functions are the solution of Eq. (7). We suppose

$$\begin{array}{ccc}\hfill S\left(t\right)-S\left(0\right)& =& S_n\left(t\right)-G_n\left(t\right),\hfill \\ \hfill E\left(t\right)-E\left(0\right)& =& E_n\left(t\right)-H_n\left(t\right),\hfill \\ \hfill I\left(t\right)-I\left(0\right)& =& I_n\left(t\right)-J_n\left(t\right),\hfill \\ \hfill R\left(t\right)-C\left(0\right)& =& R_n\left(t\right)-K_n\left(t\right).\hfill \end{array}$$ (43)

Therefore, we get

$$\begin{array}{ccc}\hfill \parallel G_n\left(t\right)\parallel & =& \left|\right|\frac{2(1-\tau )}{\mathcal{F}\left(\tau \right)(2-\tau )}(C_1(t,S)-C_1(t,S_{n-1}))+\frac{2\tau }{\mathcal{F}\left(\tau \right)(2-\tau )}{\int }_0^t(C_1(\zeta ,S)-C_1(\zeta ,S_{n-1}))d\zeta \left|\right|,\hfill \\ & \le & \frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}\parallel (C_1(t,S)-C_1(t,S_{n-1}))\parallel +\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\int }_0^t\parallel (C_1(\zeta ,S)-C_1(\zeta ,S_{n-1}))\parallel d\zeta ,\hfill \\ & \le & \frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}{\theta }_1\parallel S-S_{n-1}\parallel +\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\theta }_1\parallel S-S_{n-1}\parallel t.\hfill \end{array}$$ (44)

After repeating same process, then at $t_0$ we obtained

$$\parallel G_n\left(t\right)\parallel \le (\frac{2(1-\tau )}{\mathcal{F}\left(\tau \right)(2-\tau )}+\frac{2\tau }{\mathcal{F}\left(\tau \right)(2-\tau )}{t}_0){}^{n+1}{\theta }_1^{n+1}a.$$ (45)

As n approaches infinity, taking limit on Eq. (45) we get $\parallel G_n\left(t\right)\parallel \to 0$.

Similarly, we find $\parallel H_n\left(t\right)\to 0\parallel ,\parallel J_n\left(t\right)\to 0\parallel$ and $\parallel K_n\left(t\right)\to 0\parallel$. □

For clarity on uniqueness for the solutions of the model (7), assuming $S_1\left(t\right),$ $E_1\left(t\right),$ $I_1\left(T\right)$ and $R_1\left(t\right)$ are a distinct set of solutions pertaining to Eq. (7), then

$$S\left(t\right)-S_1\left(t\right)=\frac{2(1-\tau )}{(2-\tau )\mathcal{F}\left(\tau \right)}(C_1(t,S)-C_1(t,S_1))+\frac{2\tau }{(2-\tau )\mathcal{F}\left(\tau \right)}{\int }_0^t(C_1(\zeta ,S)-C_1(\zeta ,S_1))d\zeta .$$ (46)

Considering the fact that kernel satisfies the Lipschitz condition and taking norm on Eq. (46), prompts to the inequality given below:

$$\parallel S\left(t\right)-S_1\left(t\right)\parallel (1-\frac{2(1-\tau )}{2\mathcal{F}\left(\tau \right)-\tau \mathcal{F}\left(\tau \right)}{\theta }_1-\frac{2\tau }{2\mathcal{F}\left(\tau \right)-\tau \mathcal{F}\left(\tau \right)}{\theta }_{1}t)\le 0.$$ (47)

Theorem 5

If the following inequality holds

$$(1-\frac{2(1-\tau )}{2\mathcal{F}\left(\tau \right)-\tau \mathcal{F}\left(\tau \right)}{\theta }_1-\frac{2\tau }{2\mathcal{F}\left(\tau \right)-\tau \mathcal{F}\left(\tau \right)}{\theta }_{1}t)>0.$$

then a unique solution for the COVID-19 model(7)exists.

Proof

With the condition that (47) holds, taking

$$\parallel S\left(t\right)-S_1\left(t\right)\parallel (1-\frac{2(1-\tau )}{2\mathcal{F}\left(\tau \right)-\tau \mathcal{F}\left(\tau \right)}{\theta }_1-\frac{2\tau }{2\mathcal{F}\left(\tau \right)-\tau \mathcal{F}\left(\tau \right)}{\theta }_{1}t)\le 0.$$ (48)

So, we obtain

$$\parallel S\left(t\right)-S_1\left(t\right)\parallel =0.$$ (49)

Then,

$$S\left(t\right)=S_1\left(t\right).$$ (50)

In the same manner, we gain

$$\begin{array}{c}\hfill E\left(t\right)=E_1\left(t\right),\\ \hfill I\left(t\right)=I_1\left(t\right),\\ \hfill R\left(t\right)=R_1\left(t\right).\end{array}$$ (51)

Which verifies the proof for uniqueness of the solutions for COVID-19 model (7). □

5. Existence and uniqueness of solution for COVID-19 with Atangana-Baleanu derivative in Caputo sense (ABC).

In this section we will prove the existence and uniqueness of solution for model (6) with ABC fractional derivative operator represented by Eq. (8).

Implementing the fractional integral to both sides of Eq. (8), the model can be written as follows:

$$\begin{array}{ccc}\hfill S\left(t\right)-S\left(0\right)& =& {}_0^{ABC}{I}_t^{\tau }\{\Pi -\frac{\beta S\left(t\right)I\left(t\right)}{N}-mS\left(t\right)\},\hfill \\ \hfill E\left(t\right)-E\left(0\right)& =& {}_0^{ABC}{I}_t^{\tau }\{\frac{\beta S\left(t\right)I\left(t\right)}{N}-(m+\psi )E\left(t\right)\},\hfill \\ \hfill I\left(t\right)-I\left(0\right)& =& {}_0^{ABC}{I}_t^{\tau }\{\psi E\left(t\right)-(m+\gamma )I\left(t\right)\},\hfill \\ \hfill R\left(t\right)-R\left(0\right)& =& {}_0^{ABC}{I}_t^{\tau }\{\gamma I\left(t\right)-mR\left(t\right)\}.\hfill \end{array}$$ (52)

The notations [37], when organized within the context of the problem yield the following results;

$$\begin{array}{ccc}\hfill S\left(t\right)-S\left(0\right)& =& \frac{1-\tau }{\mathcal{B}\left(\tau \right)}\{\Pi -\frac{\beta S\left(t\right)I\left(t\right)}{N}-mS\left(t\right)\}+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}\{\Pi -\frac{\beta S\left(\zeta \right)I\left(\zeta \right)}{N}-mS\left(\zeta \right)\left)\right\}d\zeta ,\hfill \\ \hfill E\left(t\right)-E\left(0\right)& =& \frac{1-\tau }{\mathcal{B}\left(\tau \right)}\{\frac{\beta S\left(t\right)I\left(t\right)}{N}-(m+\psi )E\left(t\right)\}+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}\{\frac{\beta S\left(\zeta \right)I\left(\zeta \right)}{N}-(m+\psi )E\left(\zeta \right)\}d\zeta ,\hfill \\ \hfill I\left(t\right)-I\left(0\right)& =& \frac{1-\tau }{\mathcal{B}\left(\tau \right)}\{\psi E\left(t\right)-(m+\gamma )I\left(t\right)\}+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}\{\psi E\left(\zeta \right)-(m+\gamma )I\left(\zeta \right)\}d\zeta ,\hfill \\ \hfill R\left(t\right)-R\left(0\right)& =& \frac{1-\tau }{\mathcal{B}\left(\tau \right)}\{\gamma I\left(t\right)-mR\left(t\right)\}+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}\{\gamma I\left(\zeta \right)-mR\left(\zeta \right)\}d\zeta .\hfill \end{array}$$ (53)

We interpret for clarity;

$$\begin{array}{ccc}\hfill \overline{C_1}(t,S)& =& \Pi -\frac{\beta S\left(t\right)I\left(t\right)}{N}-mS\left(t\right),\hfill \\ \hfill \overline{C_2}(t,E)& =& \frac{\beta S\left(t\right)I\left(t\right)}{N}-(m+\psi )E\left(t\right),\hfill \\ \hfill \overline{C_3}(t,A)& =& \psi E\left(t\right)-(m+\gamma )I\left(t\right),\hfill \\ \hfill \overline{C_4}(t,C)& =& \gamma I\left(t\right)-mR\left(t\right).\hfill \end{array}$$ (54)

Theorem 6

If the inequality given below holds

$$0\le \left(\frac{\beta \overline{a}}{N}+m\right)<1,$$

then, the kernel $\overline{C_1}$ justifies the Lipschitz condition and contraction.

Proof

Assume $S$ and $S_1$ are two functions, with that we have

$$\parallel \overline{C_1}(t,S)-\overline{C_1}(t,S_1)\parallel =\left|\right|-\frac{\beta (S\left(t\right)-S\left(t_1\right))I\left(t\right)}{N}-m(S\left(t\right)-S\left(t_1\right))\left|\right|.$$ (55)

Applying the triangular inequality on Eq. (55) gives

$$\begin{array}{ccc}\hfill \parallel \overline{C_1}(t,S)-\overline{C_1}(t,S_1)\parallel & \le & \left|\right|\frac{\beta I\left(t\right)(S\left(t\right)-S\left(t_1\right))}{N}\left|\right|+\parallel m(S\left(t\right)-S\left(t_1\right))\parallel ,\hfill \\ & \le & [\frac{\beta \parallel I\left(t\right)\parallel }{N}+m]\parallel (S\left(t\right)-S\left(t_1\right))\parallel ,\hfill \\ & \le & \left[\frac{\beta \overline{a}}{N}+m\right]\parallel S\left(t\right)-S\left(t_1\right)\parallel ,\hfill \\ & \le & \overline{{\theta }_1}\parallel \{S\left(t\right)-S\left(t_1\right)\}\parallel .\hfill \end{array}$$ (56)

Let $\overline{{\theta }_1}=\frac{\beta \overline{a}}{N}+m,$ where $\parallel S\left(t\right)\parallel \le \overline{s},$ $\parallel R\left(t\right)\parallel \le \overline{r}$, $\parallel I\left(t\right)\parallel \le \overline{a}$ and $\parallel E\left(t\right)\parallel \le \overline{b}$ are bounded functions, we get

$$\parallel \overline{C_1}(t,S)-\overline{C_1}(t,S_1)\parallel \le \overline{{\theta }_1}\parallel S\left(t\right)-S\left(t_1\right)\parallel .$$ (57)

Hence, the Lipschitz condition is obtained for kernel $\overline{C_1}$ and $0\le \left(\frac{\beta \overline{a}}{N}+m\right)<1$ provides $\overline{C_1},$ which satisfies contraction.

Similarly, the other kernels $\overline{C_2},\overline{C_3}$ and $\overline{C_3}$ satisfy the Lipschitz condition and contraction.

Taking the aforementioned kernels Eq. (53) becomes

$$\begin{array}{ccc}\hfill S\left(t\right)& =& S\left(0\right)+\frac{1-\tau }{\mathcal{B}\left(\tau \right)}\overline{C_1}(t,S)+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}\left(\overline{C_1}(\zeta ,S)\right)d\zeta ,\hfill \\ \hfill E\left(t\right)& =& E\left(0\right)+\frac{1-\tau }{\mathcal{B}\left(\tau \right)}\overline{C_2}(t,E)+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}\left(\overline{C_2}(\zeta ,E)\right)d\zeta ,\hfill \\ \hfill I\left(t\right)& =& I\left(0\right)+\frac{1-\tau }{\mathcal{B}\left(\tau \right)}\overline{C_3}(t,I)+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}\left(\overline{C_3}(\zeta ,I)\right)d\zeta ,\hfill \\ \hfill R\left(t\right)& =& R\left(0\right)+\frac{1-\tau }{\mathcal{B}\left(\tau \right)}\overline{C_4}(t,R)+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}\left(\overline{C_4}(\zeta ,R)\right)d\zeta .\hfill \end{array}$$ (58)

We focus on the following recursive formulae, given as

$$\begin{array}{ccc}\hfill S_n\left(t\right)& =& \frac{1-\tau }{\mathcal{B}\left(\tau \right)}\overline{C_1}(t,S_{n-1})+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}\left(\overline{C_1}(\zeta ,S_{n-1})\right)d\zeta ,\hfill \\ \hfill E_n\left(t\right)& =& \frac{1-\tau }{\mathcal{B}\left(\tau \right)}\overline{C_2}(t,E_{n-1})+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}\left(\overline{C_2}(\zeta ,E_{n-1})\right)d\zeta ,\hfill \\ \hfill I_n\left(t\right)& =& \frac{1-\tau }{\mathcal{B}\left(\tau \right)}\overline{C_3}(t,I_{n-1})+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}\left(\overline{C_3}(\zeta ,I_{n-1})\right)d\zeta ,\hfill \\ \hfill R_n\left(t\right)& =& \frac{1-\tau }{\mathcal{B}\left(\tau \right)}\overline{C_4}(t,R_{n-1})+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}\left(\overline{C_4}(\zeta ,R_{n-1})\right)d\zeta .\hfill \end{array}$$ (59)

Along with initial conditions:

$$S_0\left(t\right)=S\left(0\right),E_0\left(t\right)=E\left(0\right),I_0\left(t\right)=I\left(0\right),R_0\left(t\right)=R\left(0\right).$$ (60)

The subsequent expressions for the difference of successive terms are expressed as:

$$\begin{array}{ccc}\hfill {\overline{\lambda }}_n\left(t\right)& =& S_n\left(t\right)-S_{n-1}\left(t\right)=\frac{1-\tau }{\mathcal{B}\left(\tau \right)}({\overline{C}}_1(t,S_{n-1})-{\overline{C}}_1(t,S_{n-2}))+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}({\overline{C}}_1(\zeta ,S_{n-1})-{\overline{C}}_1(\zeta ,S_{n-2}))d\zeta ,\hfill \\ \hfill {\overline{\omega }}_n\left(t\right))& =& E_n\left(t\right)-E_{n-1}\left(t\right)=\frac{1-\tau }{\mathcal{B}\left(\tau \right)}({\overline{C}}_2(t,E_{n-1})-{\overline{C}}_2(t,E_{n-2}))+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}({\overline{C}}_2(\zeta ,E_{n-1})-{\overline{C}}_2(\zeta ,E_{n-2}))d\zeta ,\hfill \\ \hfill {\overline{\xi }}_n\left(t\right)& =& I_n\left(t\right)-I_{n-1}\left(t\right)=\frac{1-\tau }{\mathcal{B}\left(\tau \right)}({\overline{C}}_3(t,I_{n-1})-{\overline{C}}_3(t,I_{n-2}))+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}({\overline{C}}_3(\zeta ,I_{n-1})-{\overline{C}}_3(\zeta ,I_{n-2}))d\zeta ,\hfill \\ \hfill {\overline{\eta }}_n\left(t\right)& =& R_n\left(t\right)-R_{n-1}\left(t\right)=\frac{1-\tau }{\mathcal{B}\left(\tau \right)}({\overline{C}}_4(t,R_{n-1})-{\overline{C}}_4(t,R_{n-2}))+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}({\overline{C}}_4(\zeta ,R_{n-1})-{\overline{C}}_4(\zeta ,R_{n-2}))d\zeta .\hfill \end{array}$$ (61)

It is obvious that

$$\begin{array}{c}\hfill \{\begin{array}{c}{S}_n\left(t\right)=\sum _{i=1}^n{\overline{\omega }}_i\left(t\right),\hfill \\ \\ E_n\left(t\right)=\sum _{i=1}^n{\overline{\lambda }}_i\left(t\right),\hfill \\ \\ I_n\left(t\right)=\sum _{i=1}^n{\overline{\xi }}_i\left(t\right),\hfill \\ \\ R_n\left(t\right)=\sum _{i=1}^n{\overline{\eta }}_i\left(t\right).\hfill \end{array}\end{array}$$ (62)

Applying the norm on Eq. (61), yields;

$$\parallel {\overline{\lambda }}_n\left(t\right)\parallel =\parallel S_n\left(t\right)-S_{n-1}\left(t\right)\parallel =\left|\right|\frac{1-\tau }{\mathcal{B}\left(\tau \right)}({\overline{C}}_1(t,S_{n-1})-{\overline{C}}_1(t,S_{n-2}))+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}({\overline{C}}_1(\zeta ,S_{n-1})-{\overline{C}}_1(\zeta ,S_{n-2}))d\zeta \left|\right|.$$ (63)

Applying the triangular inequality, Eq. (63) reduces to

$$\parallel S_n\left(t\right)-S_{n-1}\left(t\right)\parallel \le \frac{1-\tau }{\mathcal{B}\left(\tau \right)}\left|\right|({\overline{C}}_1(\zeta ,S_{n-1})-{\overline{C}}_1(\zeta ,S_{n-2}))\left|\right|+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}\left|\right|{\int }_0^t{(t-\zeta )}^{\tau -1}({\overline{C}}_1(\zeta ,S_{n-1})-{\overline{C}}_1(\zeta ,S_{n-2}))d\zeta \left|\right|.$$ (64)

Since, the kernel ${\overline{C}}_1$ satisfies the Lipschitz condition, we have

$$\parallel S_n\left(t\right)-S_{n-1}\left(t\right)\parallel \le \frac{1-\tau }{\mathcal{B}\left(\tau \right)}{\overline{\theta }}_1\parallel S_{n-1}-S_{n-2}\parallel +\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\overline{\theta }}_1{\int }_0^t{(t-\zeta )}^{\tau -1}\parallel S_{n-1}-S_{n-2}\parallel d\zeta .$$ (65)

Therefore, we conclude;

$$\parallel {\overline{\lambda }}_n\left(t\right)\parallel \le \frac{1-\tau }{\mathcal{B}\left(\tau \right)}{\overline{\theta }}_1\parallel {\overline{\lambda }}_{n-1}\left(t\right)\parallel +\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\overline{\theta }}_1{\int }_0^t{(t-\zeta )}^{\tau -1}\parallel {\overline{\lambda }}_{n-1}\left(\zeta \right)\parallel d\zeta .$$ (66)

Similarly, we gain the subsequent results

$$\begin{array}{ccc}\hfill \parallel {\overline{\omega }}_n\left(t\right))\parallel & \le & \frac{1-\tau }{\mathcal{B}\left(\tau \right)}{\overline{\theta }}_2\parallel {\overline{\omega }}_{n-1}\left(t\right)\parallel +\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\overline{\theta }}_2{\int }_0^t{(t-\zeta )}^{\tau -1}\parallel {\overline{\omega }}_{n-1}\left(\zeta \right)\parallel d\zeta ,\hfill \\ \hfill \parallel {\overline{\xi }}_n\left(t\right)\parallel & \le & \frac{1-\tau }{\mathcal{B}\left(\tau \right)}{\overline{\theta }}_3\parallel {\overline{\xi }}_{n-1}\left(t\right)\parallel +\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\overline{\theta }}_3{\int }_0^t{(t-\zeta )}^{\tau -1}\parallel {\overline{\xi }}_{n-1}\left(\zeta \right)\parallel d\zeta ,\hfill \\ \hfill \parallel {\overline{\eta }}_n\left(t\right)\parallel & \le & \frac{1-\tau }{\mathcal{B}\left(\tau \right)}{\overline{\theta }}_4\parallel {\overline{\eta }}_{n-1}\left(t\right)\parallel +\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\overline{\theta }}_4{\int }_0^t{(t-\zeta )}^{\tau -1}\parallel {\overline{\eta }}_{n-1}\left(\zeta \right)\parallel d\zeta .\hfill \end{array}$$ (67)

 □

Considering the above results, we present the following theorem:

Theorem 7

The COVID-19 fractional model(8)has a solutions if we can find a$t_0,$such that:

$$\frac{1-\tau }{\mathcal{B}\left(\tau \right)}{\overline{\theta }}_i+\frac{t_0^{\tau }}{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\overline{\theta }}_i<1$$

for i=1,2,3,4.

Proof

Considering the Eqs. (66) and (67), along with the fact that functions $S\left(t\right),$ $E\left(t\right),$ $I\left(t\right)$ and $R\left(t\right)$ are bounded and the kernels justify the Lipschitz condition. We have the following relation employing the recursive method:

$$\begin{array}{ccc}\hfill \parallel {\overline{\lambda }}_n\left(t\right)\parallel & \le & \parallel S_n\left(0\right)\parallel \left[\right(\frac{1-\tau }{\mathcal{B}\left(\tau \right)}\overline{{\theta }_1})+(\frac{t_0^{\tau }}{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\overline{\theta }}_1\left)\right]{}^n,\hfill \\ \hfill \parallel {\overline{\omega }}_n\left(t\right))\parallel & \le & \parallel E_n\left(0\right)\parallel \left[\right(\frac{1-\tau }{\mathcal{B}\left(\tau \right)}\overline{{\theta }_2})+(\frac{t_0^{\tau }}{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\overline{\theta }}_2\left)\right]{}^n,\hfill \\ \hfill \parallel {\overline{\xi }}_n\left(t\right)\parallel & \le & \parallel A_n\left(0\right)\parallel \left[\right(\frac{1-\tau }{\mathcal{B}\left(\tau \right)}\overline{{\theta }_3})+(\frac{t_0^{\tau }}{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\overline{\theta }}_3\left)\right]{}^n,\hfill \\ \hfill \parallel {\overline{\eta }}_n\left(t\right)\parallel & \le & \parallel C_n\left(0\right)\parallel \left[\right(\frac{1-\tau }{\mathcal{B}\left(\tau \right)}{\overline{\theta }}_4)+(\frac{t_0^{\tau }}{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\overline{\theta }}_4\left)\right]{}^n.\hfill \end{array}$$ (68)

We demonstrate solutions exist and also satisfy continuity, for the COVID-19 model (8). For the sake of clarity, the above functions are the solution of Eq. (8). We suppose

$$\begin{array}{ccc}\hfill S\left(t\right)-S\left(0\right)& =& S_n\left(t\right)-{\overline{G}}_n\left(t\right),\hfill \\ \hfill E\left(t\right)-E\left(0\right)& =& E_n\left(t\right)-{\overline{H}}_n\left(t\right),\hfill \\ \hfill I\left(t\right)-I\left(0\right)& =& I_n\left(t\right)-{\overline{J}}_n\left(t\right),\hfill \\ \hfill R\left(t\right)-C\left(0\right)& =& R_n\left(t\right)-{\overline{K}}_n\left(t\right).\hfill \end{array}$$ (69)

Therefore, we get

$$\begin{array}{ccc}\hfill \parallel {\overline{G}}_n\left(t\right)\parallel & =& \left|\right|\frac{1-\tau }{\mathcal{B}\left(\tau \right)}({\overline{C}}_1(t,S)-{\overline{C}}_1(t,S_{n-1}))+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}({\overline{C}}_1(\zeta ,S)-{\overline{C}}_1(\zeta ,S_{n-1}))d\zeta \left|\right|,\hfill \\ & \le & \frac{1-\tau }{\mathcal{B}\left(\tau \right)}\parallel ({\overline{C}}_1(t,S)-{\overline{C}}_1(t,S_{n-1}))\parallel +\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}\parallel ({\overline{C}}_1(\zeta ,S)-{\overline{C}}_1(\zeta ,S_{n-1}))\parallel d\zeta ,\hfill \\ & \le & \frac{1-\tau }{\mathcal{B}\left(\tau \right)}{\theta }_1\parallel S-S_{n-1}\parallel +\frac{t^{\tau }}{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\overline{\theta }}_1\parallel S-S_{n-1}\parallel .\hfill \end{array}$$ (70)

After repeating same process, then at $t_0$ we obtained

$$\parallel {\overline{G}}_n\left(t\right)\parallel \le (\frac{1-\tau }{\mathcal{B}\left(\tau \right)}+\frac{t_0^{\tau }}{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}){}^{n+1}{\overline{\theta }}_1^{n+1}M.$$ (71)

As n approaches infinity, taking limit on Eq. (71) we get $\parallel {\overline{G}}_n\left(t\right)\parallel \to 0$.

Similarly, we find $\parallel {\overline{H}}_n\left(t\right)\to 0\parallel ,\parallel {\overline{J}}_n\left(t\right)\to 0\parallel$ and $\parallel {\overline{K}}_n\left(t\right)\to 0\parallel$. □

For clarity on uniqueness for the solutions of the model (8), assuming $S_1\left(t\right),$ $E_1\left(t\right),$ $I_1\left(T\right)$ and $R_1\left(t\right)$ are a distinct set of solutions pertaining to Eq. (8), then

$$S\left(t\right)-S_1\left(t\right)=\frac{1-\tau }{\mathcal{B}\left(\tau \right)}({\overline{C}}_1(t,S)-{\overline{C}}_1(t,S_1))+\frac{\tau }{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\int }_0^t{(t-\zeta )}^{\tau -1}({\overline{C}}_1(\zeta ,S)-{\overline{C}}_1(\zeta ,S_1))d\zeta .$$ (72)

Considering the fact that kernel satisfies the Lipschitz condition and taking norm on Eq. (72), prompts to the inequality:

$$\parallel S\left(t\right)-S_1\left(t\right)\parallel (1-\frac{1-\tau }{\mathcal{B}\left(\tau \right)}{\overline{\theta }}_1-\frac{t^{\tau }}{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\overline{\theta }}_1)\le 0.$$ (73)

Theorem 8

If the following inequality holds

$$(1-\frac{1-\tau }{\mathcal{B}\left(\tau \right)}{\overline{\theta }}_1-\frac{t^{\tau }}{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\overline{\theta }}_1)>0.$$

then a unique solution for the COVID-19 model(8)exists.

Proof

With the condition that (73) holds, taking

$$\parallel S\left(t\right)-S_1\left(t\right)\parallel (1-\frac{1-\tau }{\mathcal{B}\left(\tau \right)}{\overline{\theta }}_1-\frac{t^{\tau }}{\mathcal{B}\left(\tau \right)\Gamma \left(\tau \right)}{\overline{\theta }}_1)\le 0.$$ (74)

So, we obtain

$$\parallel S\left(t\right)-S_1\left(t\right)\parallel =0.$$ (75)

Then,

$$S\left(t\right)=S_1\left(t\right).$$ (76)

In the same manner, we gain

$$\begin{array}{c}\hfill E\left(t\right)=E_1\left(t\right),\\ \hfill I\left(t\right)=I_1\left(t\right),\\ \hfill R\left(t\right)=R_1\left(t\right).\end{array}$$ (77)

Which verifies the proof for uniqueness of the solutions for COVID-19 model (8). □

6. Numerical results and discussion

In this section, we provide the numerical simulations using Matlab for both CF approach and ABC approach model mentioned in Eqs. (7) and (8) respectively. Next, we compare and discuss the following results.

Caputo-Fabrizio sense.

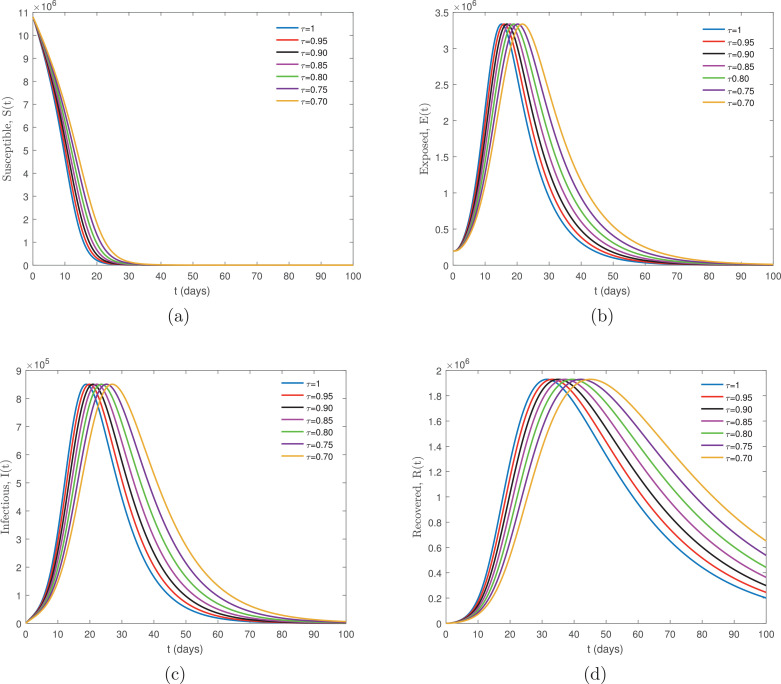
Using Wuhan City as an example, we created the following framework: $\Pi =0.36,$ $\beta =2.5-5,$ $m=0.30,$ $\psi$ represents the mean latency period of COVID-19 in humans, considering 14 days, $\psi =1/14,$ $\gamma$ represents the infectious period in days. Considering 5 days, $\gamma =1/5$. The initial conditions are given by $S\left(0\right)=108\times 10{}^5,$ $E\left(0\right)=2\times 10{}^5,$ $I\left(0\right)=278$ and $R\left(0\right)=0,$ all values were assumed. The dynamics of the new Coronavirus Disease COVID-19 model involving the non-singular fractional derivative of Caputo-Fabrizio type is given by Eq. (7) for various values of $\tau \in (0,1],$ arbitrarily chosen, are plotted in Fig. 1 a–d.

Fig. 1.

Numerical simulation for the new Coronavirus Disease COVID-19 model involving the Caputo-Fabrizio derivative given by Eq. (7) for several values of $\tau ,$ arbitrarily chosen.

Atangana-Baleanu-Caputo sense.

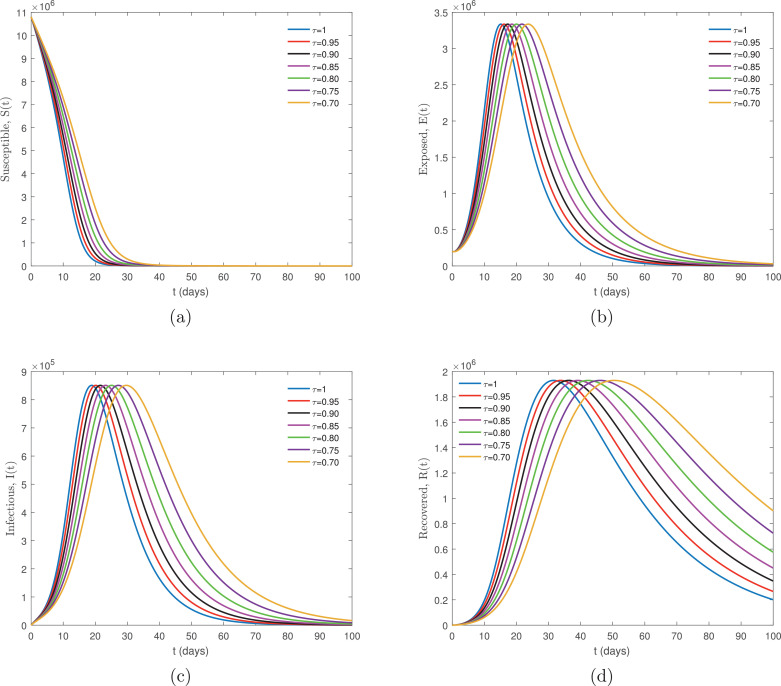
Again, using Wuhan City as an example we created the following: $\Pi =0.36,$ $\beta =2.5-5,$ $m=0.30,$ $\psi$ represents the mean latency period of COVID-19 in humans, considering 14 days, $\psi =1/14,$ $\gamma$ represents the infectious period in days. Considering 5 days, $\gamma =1/5$. The initial conditions are given by $S\left(0\right)=108\times 10{}^5,$ $E\left(0\right)=2\times 10{}^5,$ $I\left(0\right)=278$ and $R\left(0\right)=0,$ all values were assumed. The dynamics of the new Coronavirus Disease COVID-19 model involving the non-singular fractional derivative of Atangana-Baleanu type is given by Eq. (8) for various values of $\tau \in (0,1],$ arbitrarily chosen, are plotted in Fig. 2 a–d.

Fig. 2.

Numerical simulation for the new Coronavirus Disease COVID-19 model involving the Atangana-Baleanu derivative given by Eq. (8) for several values of $\tau ,$ arbitrarily chosen.

The numerical simulations’ comparison of Figs. 1a–d and 2 a–d for both the CF model (7) and ABC model (8) demonstrates that for $\tau =1$ with same the initial conditions and parameter values gives identical output. Whereas, for the same non integer values of $\tau ,$ both models show dissimilar trajectories. Thus, observation finds that smaller $\tau$ susceptible populations decrease at a slower rate with the ABC approach compared to the CF approach. It is clearly visible from graph Fig. 1(b)–(c) and Fig. 2(b)–(c) comparisons that the ABC approach provides comparatively more variation in both infected and recovered individuals than the CF approach, which is more likely to suit real data. Another important aspect considers that exposed and infected individuals show a sharp increase for all values of $\tau$ due to the high transmissibility of COVID-19 of the disease advocated by Karako et al. [26].

Furthermore, upon deep consideration of the comparisons indicated in graph Fig 1(c) with (d) we find a difference of approximately 2 weeks between the peak of infected and recovered individuals. However, notably in Fig 2(c) with (d) the difference between the peak points is 3 weeks, calculated at $\tau =0.7$. The slope of curves for other values of $\tau$ share similarities with the findings. This indicates that infected individuals are recovering very quickly, with a delay of approximately 2 weeks, shown by the CF approach, which is valid for mild cases. Conversely, the ABC approach shows approximately a 3-week delay in the transfer of infected individuals to recovered compartments. This is valid for severe or critical disease states, as per the WHO-China Joint Mission on Coronavirus Disease 2019 (COVID-19) report [41].

The effectiveness of both models, when compared, found notable differences under identical parameter values. This is due to the memory properties of the kernel in the definitions of the fractional operators. The Caputo-Fabrizio derivative has an exponential kernel, whereas the ABC approach uses a generalized Mittag-Leffler kernel. The latter shows a partial exponential decay memory, and also power-law memory (see [42], [43]). It is clear from the above simulation graphs that the model relies upon the fractional order remarkably, for various values of $\tau$ it displays a clear difference. The suggested model explores new aspects at the fractional value of $\tau ,$ which is inappreciable for the model at $\tau =1$.

7. Conclusion

Disease-relevant contact increases with an escalation in population size. Thus, Coronavirus disease COVID-19 transmission non-integer order model is considered, using the CF derivative and ABC derivative (with standard incidence) are formulated. Expression for the basic reproduction number along with equilibrium points and their local stability are analyzed. The uniqueness and existence is verified by employing the fixed-point theorem for both CF and ABC models. Numerical simulation graphs for the proposed COVID-19 fractional order models are shown with distinct fractional order values $\tau \in (0,1]$ and briefly compared, discussed and investigated. The graphical results demonstrate the CF approach provides better suitability for mild cases (studies suggest approximately 80% of patients have had mild disease). Whereas, the ABC approach provides superior and more flexible results for critical cases. These results show that CF and ABC approach implementation in real life situations are both plausible and doable as per the severity of illness for patient management.

For future research work we propose COVID-19 spread for different geographical areas can be achieved by examining the models with relevant parameter values as per data trends of the region. We anticipate this research will provide significance and will thus strengthen the research relevant to COVID-19 transmission dynamics, so that progressive disease control policies are formulated to provide patients with better medical care for all in need.

Authorship statement

Conception and design of study: Virender Singh Panwar; Acquisition of data: Virender Singh Panwar; Analysis and/or interpretation of data: Virender Singh Panwar, P.S. Sheik Uduman. Category 2 Drafting the manuscript: Virender Singh Panwar, J.F. Gómez-Aguilar; Revising the manuscript critically for important intellectual content: Virender Singh Panwar, J.F. Gómez-Aguilar. Category 3 Approval of the version of the manuscript to be published Virender Singh Panwar, P.S. Sheik Uduman, J.F. Gómez-Aguilar.

Declaration of Competing Interest

None.