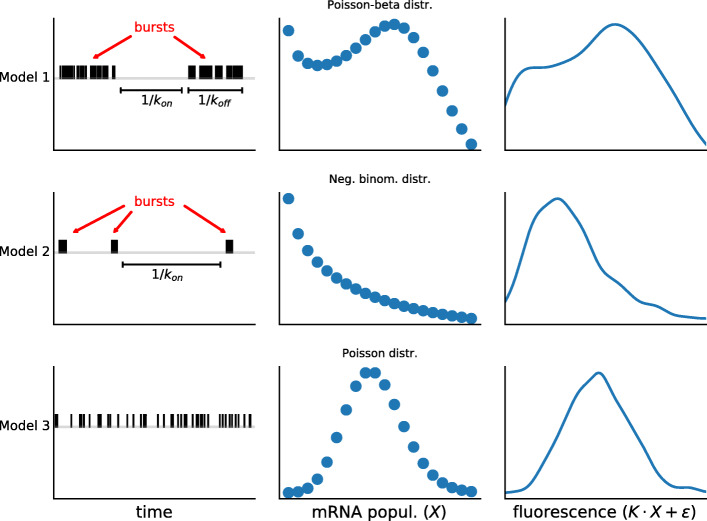
Fig. 2.
Relations between transcriptional mechanisms, mRNA distributions, model fitting, and parameter estimates. The timing of transcription events at a gene is important. If a population of isogenic cells is induced to express a certain gene, then the resulting mRNA numbers in each cell will reflect the dynamic properties of the process of transcription. While higher frequencies of transcription events unsurprisingly will boost mRNA numbers, more complex patterns can be identified; if transcription occurs clustered in time, forming “bursts” of mRNA production, then the variability of mRNA numbers among individual cells will increase. The precise nature of these relations depends on the mRNA half-life and other dynamical parameters. In fact, these parameters in general shape the distribution of mRNAs among cells in characteristic ways. We can exploit this by testing which parameter values and models are compatible with experimentally derived mRNA distributions and thus infer the dynamics of the underlying transcription process. In combination with experimental perturbations, this produces mechanistic insights into transcription. We applied this approach to our datasets and test their agreement with three models of nested complexity, in line with Occam’s razor. The most complex model corresponds to the transcriptional bursting described above and predicts intricate mRNA distributions, subject to several parameters. Estimating koff and kon for instance allows us to determine the average times (as their inverse) the genes spend transcribing and non-transcribing, respectively (Model 1). The second model restricts the duration of the bursts and has fewer parameters (Model 2), while the third assumes that the transcriptional events are homogeneous over time (Model 3). These models generate mRNA counts X and, in turn, fluorescence intensity, which also depends on the scaling factor κ and the measurement noise ε. To determine which models and parameters best explain our data, we used a Bayesian approach. Broadly speaking, this makes use of the so-called Bayes’ theorem to determine the probability of a hypothesis conditional to experimental data. The power of this approach is that it allows the construction of very complex settings from conditional and prior probabilities, which can be computationally explored by means of Markov chain Monte Carlo (MCMC) sampling and produce results which again are probabilities. In general, prior probabilities refer to general assumptions that are taken into account independently of the experimental data, while posterior probabilities result as informed output of the Bayesian inference procedure. The latter correspond to probability distributions of the model parameters, which thus permit excellent assessment of the uncertainties associated with the results. For our study, Bayesian inference was ideal; it allowed us to embed in a single probabilistic framework the data for multiple independent replicates, the measurement precision of our calibration experiments, and the data transformation introduced by the flow cytometer. At the same time, it produced posterior distributions that are highly informative