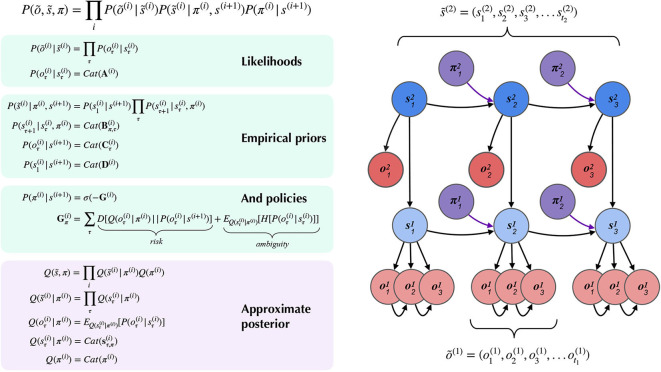
Figure 4.
A partially-observed Markov Decision Process with two hierarchical layers. Schematic overview of the generative model for a hierarchical partially-observed Markov Decision Process. The generic forms of the likelihoods, priors, and posteriors at hierarchical levels are provided in the left panels, adapted with permission from Friston et al. (2017d). Cat(x) indicates a categorical distribution, and indicates a discrete sequence of states or random variables: . Note that priors at the highest level (Level 2) are not shown, but are unconditional (non-empirical) priors, and their particular forms for the scene construction task are described in the text. As shown in the “Empirical Priors” panel, prior preferences at lower levels can be a function of states at level i + 1, but this conditioning of preferences is not necessary, and in the current work we pre-determine prior preferences at lower levels, i.e., they are not contextualized by states at higher levels (see Figure 8). Posterior beliefs about policies are given by a softmax function of the expected free energy of policies at a given level. The approximate (variational) beliefs over hidden states are represented via a mean-field approximation of the full posterior, such that hidden states can be encoded as the product of marginal distributions. Factorization of the posterior is assumed across hierarchical layers, across hidden state factors (see the text and Figures 6, 7 for details on the meanings of different factors), and across time. “Observations” at the higher level (õ(2)) may belong to one of two types: (1) observations that directly parameterize hidden states at the lower level via the composition of the observation likelihood one level P(o(i + 1)|s(i + 1)) with the empirical prior or “link function” P(s(i)|o(i + 1)) at the level below, and (2) observations that are directly sampled at the same level from the generative process (and accompanying likelihood of the generative model P(o(i + 1)|s(i + 1))). For conciseness, we represent the first type of mapping, from states at i + 1 to states at i through a direct dependency in the Bayesian graphical model in the right panel, but the reader should note that in practice this is achieved via the composition of two likelihoods: the observation likelihood at level i + 1 and the link function at level i. This composition is represented by a single empirical prior P(s(i)|s(i + 1)) = Cat(D(i)) in the left panel. In contrast, all observations at the lowest level (õ(1)) feed directly from the generative process to the agent.