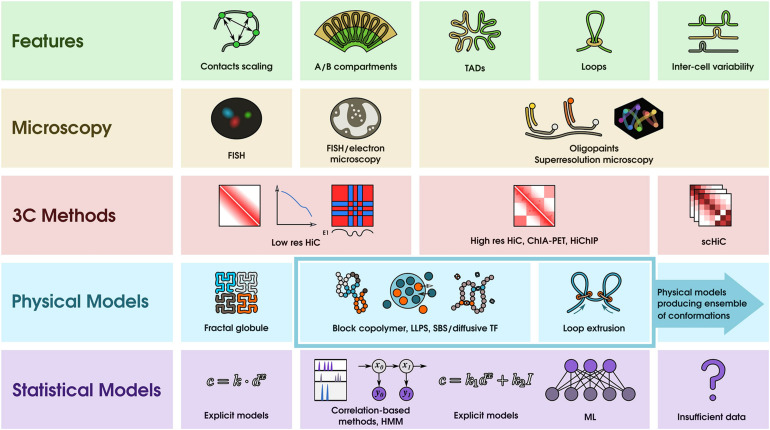
FIGURE 1.

Modeling and predicting the main features of the 3-D-genome organization using physical and statistical approaches. The features row contains a schematic representation of the main features of 3-D-genome organization: scaling of contacts with genomic distance, compartments, TADs, loops, and inter-cell variability of genome architecture (from left to right). The 3C methods row shows that contact scaling and compartments could be found using low-resolution Hi-C data, whereas identification of loops and dissection of TAD structure requires high resolution. Studying inter-cell variability is challenging and could be done using single-cell Hi-C approaches (scHi-C). Microscopy methods shown in the second row include conventional 3D-FISH (fluorescent in situ hybridization) to measure spatial distances; electron microscopy, which is helpful to visualize segregation of eu- and heterochromatin; and modern super-resolution microscopy methods, which, in combination with oligopaints, allow dissection of the internal structure of TADs in individual cells (Boettiger and Murphy, 2020; Szabo et al., 2020). Physical description of chromatin interactions (fourth row) includes generic models such as the fractal globule as well as locus-specific models. For the latter, researchers employ block-copolymer models and models with chromatin binders, such as strings and binders switch (SBS) and diffusive transcription factor (TF) models and concepts of liquid–liquid phase separation (LLPS). All these physical models allow studying the dynamics and inter-cell variability of 3-D structures, providing ensembles of possible chromatin conformations (this is schematically shown in the last cell of the physical models row). Statistical methods (the last row) could utilize interconnections between epigenetic data and chromatin organization using different approaches. This includes approaches in which explicitly defined algebraic expressions contain free parameters, which could be fit from the data, hidden Markov models (HMM), and various machine learning (ML) algorithms. TADs, loops, and compartments were predicted using these methods. However, for single-cell data, these approaches are not applicable, mainly due to the large amount of data required for the implementation of these algorithms.