Fig. 4. Attraction and stabilities of the homogeneous vegetation state, as well as resilience of transient FCs and persistent Turing-like FCs.

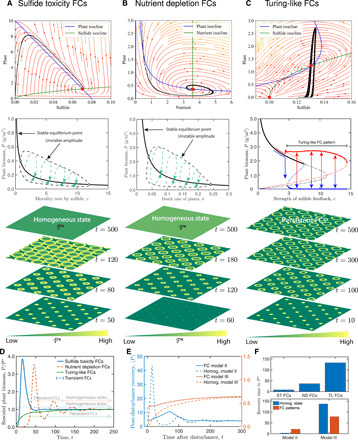
(A to C) Dynamics behaviors of three self-organized mechanisms of FC patterning. Top row: Attraction and stability of the positive equilibrium (vegetation state) with the phase portrait of system kinetics for transient and persistent FCs. Both transient FCs are global asymptotic stability, whereas persistent FCs are local asymptotic stability. Middle row: Bifurcation diagrams showing the amplitudes of FC patterned solutions and their stability were plotted in terms of plant biomass as a function of the parameter, c. Solid lines mark stable portions of the branch; dashed lines mark unstable portions. Bottom row: Typical spatial patterns and transition from the same spatial regular seedling clusters to FCs or a homogeneous steady state. (D) Trajectories of the distinctive patterned models when they return to pre-disturbance equilibrium after a temporary disturbance. (E) Recovery speed of the transient FCs and persistent FCs for self-organized patterns and spatial homogeneous scenarios. For all simulations, the plants were seeded at 40% of their positive equilibrium point (P*, red solid circles as shown in the top row). (F) Statistical comparisons for the recovery time of FC patterns among simulation models as well as the homogeneous state. Here, time was taken for 95% recovery to P*. ST FCs, sulfide toxicity FCs; ND FCs, nutrient depletion FCs; TL FCs, Turing-like FCs. The actual phase planes were shown for models with parameter values listed in table S1.