Fig. 3. Computational model for collective Cin8 motion.

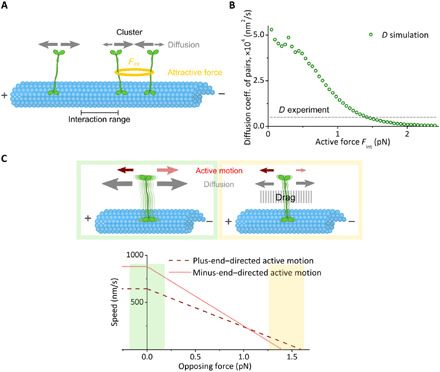
(A) The diffusive module simulates Cin8 motors as random walkers with symmetric dynamics (gray arrows) due to Brownian motion. Motors attract each other if they are within the interaction range R. The attractive force F_int (yellow ring) is assumed to be constant for distances <R and zero otherwise. Attractive interactions affect motor dynamics (detailed balance) (see the main text and section SB1). (B) The diffusion coefficient of pairs of Cin8 in simulations focusing on the diffusive module (circles) decreased with increasing attractive forces F between motors. Attractive forces of 1.4 pN result in a diffusion coefficient for Cin8 pairs that corresponds to that identified in vitro (dashed line; see also Table 1, i). (C) Top: Cin8 dynamics in the full computational model is composed of bidirectional active motion (red/pink arrows) and a diffusive component (gray arrows; illustrated by motor blurring). In the absence of an opposing force, the minus-end–directed active component is larger than the plus-end–directed component. Both the active and diffusive components are affected by opposing forces, referred to as drag (gray area in the top right). Drag suppresses Brownian motion exponentially, and minus-end–directed active motion (pink) is more strongly impeded by drag than is plus-end–directed active motion (red), such that the overall directionality switches under large drag. Bottom: The assumed force-velocity relation used in simulations, with green shading corresponding to low drag (top left) and yellow shading corresponding to high drag (top right). The sizes of the arrows are chosen for illustrative purposes only.