Fig. 1.

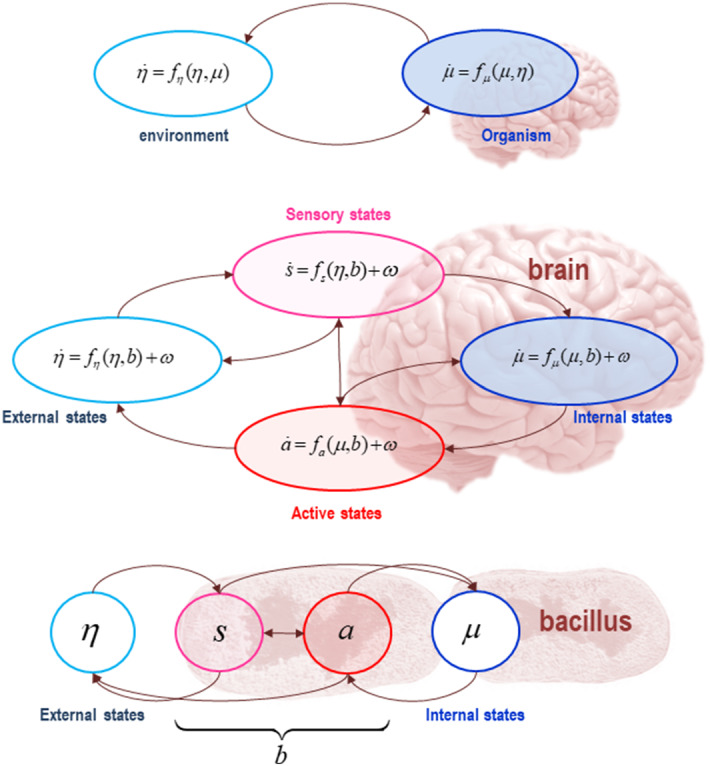
The Markov blanket and active inference. A Markov blanket is a set of states that enshrouds or statistically isolates internal states from external or hidden states. This figure depicts the partition of the states into internal ($\mu$) and external states ($\eta$). In the parlance of graph theory, the Markov blanket is a set of nodes that shields the internal states (or nodes) from the influence of external states; in the sense that internal states can only be affected by external states indirectly, via the blanket states (Friston et al. 2017b). Internal and external states are therefore separated, in a statistical sense, by the Markov blanket ($b$), which itself comprises sensory ($s$) and active states ($a$)—defined as blanket states that are and are not influenced by external states respectively. The top panel schematises the relations of reciprocal causation that couple the organism to its ecological niche, and back again. Internal states of the organism change as a function of its current state ($\mu$) and the state of its niche ($\eta$), which is expressed in terms of a flow $f_{\mu }(\mu ,\eta )$ with random fluctuations. Reciprocally, states of the niche change over time as a function of the current state of the environment and the organism, again, specified in terms of a flow $f_{\eta }(\eta ,\mu )$ with random fluctuations. The self-organisation of internal states in this scheme corresponds to perception. Active states couple internal states back to states of the niche, and so correspond to the actions of an organism. Given the anti-symmetric conditional dependencies entailed by the presence of the Markov blanket, the dynamics of the niche, too, can be expressed as a gradient flow of a free energy functional of external and blanket states. The lower panel depicts the dependencies as they would apply to a unicellular organism. In this panel, the internal states are associated with the intracellular states of a cell, the sensory states are associated with surface states of the cell membrane, and the active states are associated with the actin filaments of the cytoskeleton.

Adapted from Constant et al. (2018b)