Figure 1:

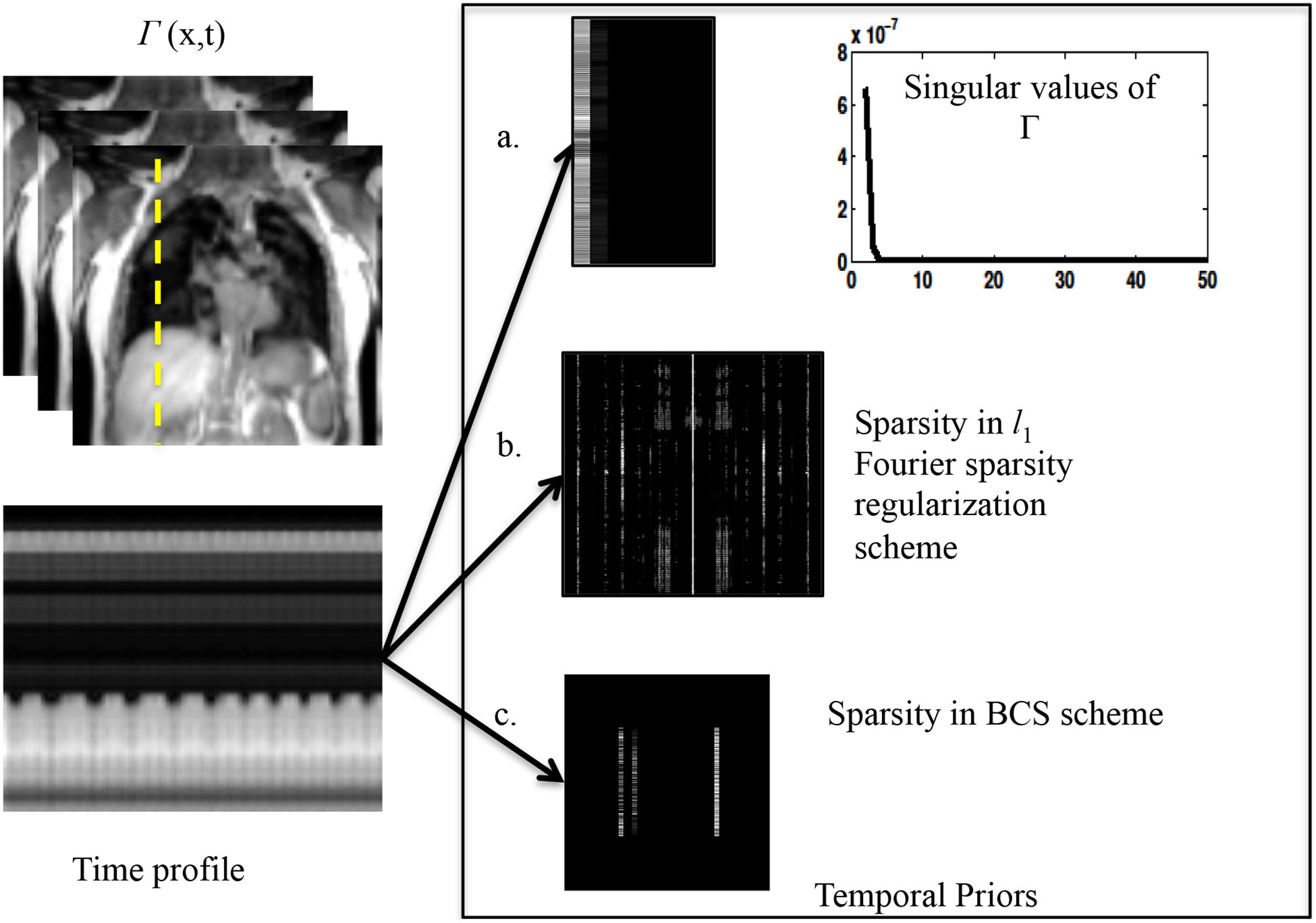
Illustration of the data representation in different transform domains: The nuclear norm minimization scheme, the l₁ Fourier sparsity regularization scheme, and the BCS scheme relies on constrained modeling of the intensity profiles of the voxels, specified by Γ = UV. The nuclear norm minimization scheme capitalizes on the efficient representation of the voxel profiles using few basis functions. The coefficients in U, along with the singular values are shown in a. The singular values of the data (Γ) decay rapidly to zero indicating that the data can be represented efficiently using few basis functions. The pseudo-periodicity of the data is exploited by l₁ Fourier sparsity regularization scheme, using the sparse representation of the intensity profiles in the temporal Fourier transform (x-f space) as seen in 1.b. Figure 1.c shows the sparse coefficients obtained from the BCS scheme. BCS, similar to nuclear norm minimization scheme, learns the dictionary of the basis functions from the data itself, thus adapting to the dynamic content of the time series. The adaptation of the dictionary to the signal provides sparser representations, which in turn translates to improved reconstructions.