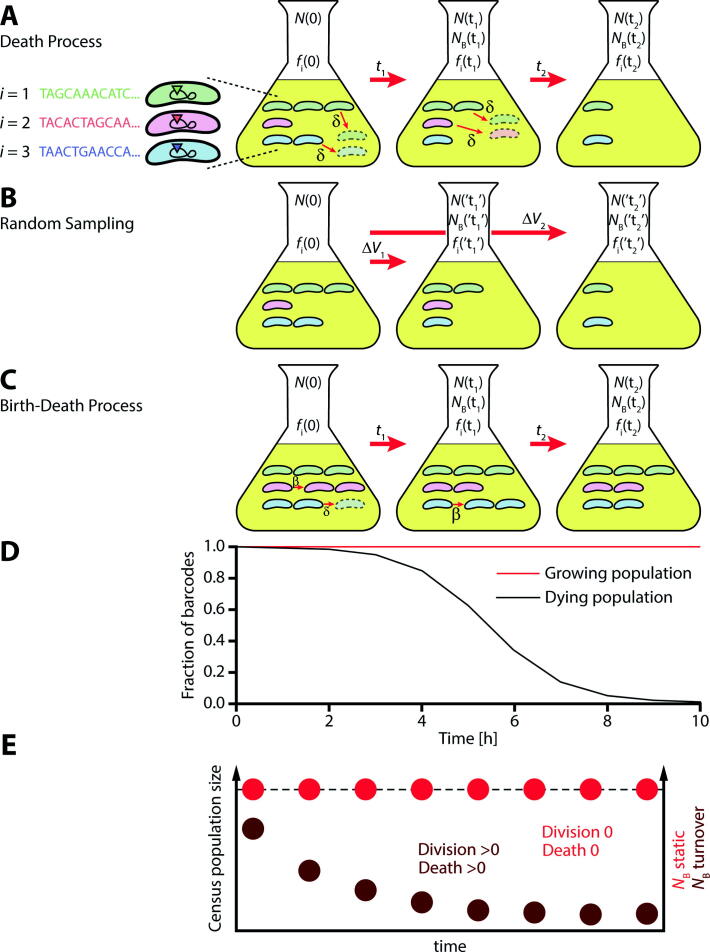
Fig. 1.

Schematic of the experimental setups. (A) Illustrates a pure death process for a population of bacteria with i = 1, 2, 3,…,k = 1000 unique 30 base pairs sequence tags at a fitness neutral location in the genome. The three magnified cells illustrate the genome within the bacteria (black circle) with potential fitness neutral locations (rectangles) and the fitness neutral location with a sequence tag (color of rectangle/bacterium). The i:th subpopulation is initially present with a frequency f_i(0) where the total population size is N(0). The bacteria undergo random death events for a length of time t₁ with rate δ per unit time after which the total population size is N(t₁) and the frequency of the i:th subpopulation is f_i(t₁). The founder population size at time t₁, N_B(t₁), is calculated by comparing the frequency of bacteria at time t₁ with the initial frequency, f_i(0) (equation (1)). After an elapsed time t₂ > t₁ fewer cells remain with N(t₂) < N(t₁) and N_B(t₂) < N_B(t₁). (B) Random sampling of the initial population with the aim of emulating a pure death process. The volume ${\mathrm{\Delta }v}_t$ is sampled from a large volume in which tagged bacteria are suspended such that the number of cells sampled is equal to the number of cells having undergone a death process for a length of time t (A). The founder population size, N_B(‘t₁′), and the population size, N(‘t₁′), are determined in the sample Δv_t and are used to estimate the death rate, δ, as it would be in a pure death process (see 5.1 – Emulating a death process by sampling). The random sampling process in itself is not a real time-dependent process, which is indicated by apostrophes around t. (B) A birth–death process that includes both death events and division events with rate δ per unit time and β per unit time, respectively. By measuring the total population size and the genetic drift in terms of the founder population size the division rate and death rate can be estimated. (D) Simulation for tag loss in two populations with the same initial composition but different growth and death rates. The mathematical framework from [21] was adopted to investigate the mean fraction of unique sequence tags (y-axis, RESTAMP) that survives until time t (x-axis) in a birth–death process. The black line represents a population that dies more quickly than it replicates. The red line represents a population that replicates more than it dies. The parameters for the simulation are the same as in Figure Supplementary Fig. 1. (E) Schematic representation of the simultaneous change in census population size (black dotted line) and founding population size (red dots) for two different sets of division and death rates (light and dark red, respectively). For both scenarios, the census population size, i.e. the total number of cells remains constant. However, depending on the magnitude of the rates, different profiles for N_B emerge over time. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)