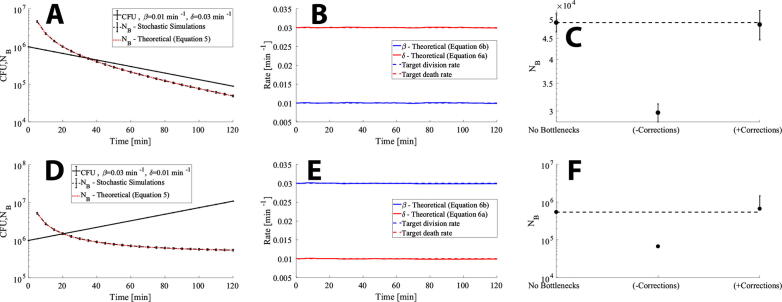
Fig. 3.
The theoretical framework for RESTAMP agrees well with stochastic tau-leaping simulations. (A) A population of k = 1000 distinguishable cells undergo a random birth–death process with δ = 0.03 min−1 and β = 0.01 min−1 for 120 min with a geometrical tag distribution at t = 0 with the probability parameter set to 1/1000. The stochastic tau-leaping simulations were ran using StochKit2 [24] with a time-step 0.01 for 100 iterations. A custom script for generating the input file to StochKit2 is available on SourceForge (see 6 – Code). The proportion of subpopulations was determined for each time point and the founder population size was calculated using equation (1). The mean founder population size and the standard deviation were next determined and plotted as a function of time (black dashed line). The CFU were calculated by summing the i = 1,2,…,k subpopulations at each time point after which the mean (over iterations) CFU and the standard deviation were determined (black solid line). The theoretical founder population size values were calculated using equation (5) (red dotted line). (B) Using the mean CFU and mean NB values illustrated in (A) we estimate the division rate and death rate over time using equations (6ab). (C) The population of cells at t = 120 min undergo two sequential multinomial random sampling events (technical bottlenecks) where the sample sizes S1 = 105 and S2 = 106 were taken. The inoculum (population at t = 0) also underwent two sequential random sampling events where the sample sizes I1 = I2 = 106 were taken. The founder population size was then calculated according to equation (1) which does not include bottleneck corrections and equation (7) which includes bottleneck corrections. The target founder population size without any technical bottlenecks is also shown and corresponds to the founder population size at t = 120 min before sampling. (D-F) Same as (A-C) except δ = 0.01 min−1 and β = 0.03 min−1. The lower bound for the standard deviation in (F) is not shown on a log scale since it is negative, i.e. the standard deviation is larger than the mean NB value. The mean and the standard deviation of the founder population size values are <NB>={5.5 × 105, 6.6 × 104, 6.1 × 105 and Std(NB)={2.5 × 104, 3.2 × 103, 7.1 × 105} for the results plotted in (F). The corresponding values for (C) are <NB>={4.9 × 104, 3.0 × 104, 4.9 × 104} and Std(NB)={2.5 × 103, 1.5 × 103, 4.1 × 103}. All scripts for reproducing these results are provided on SourceForge (see 6 – Code). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)