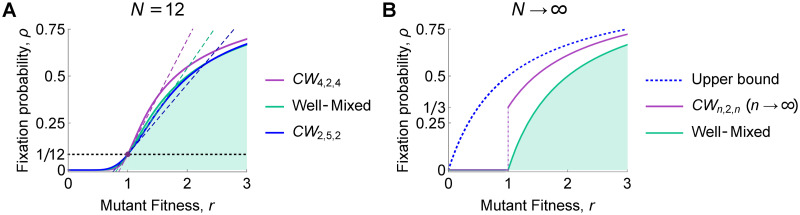
Fig 10. Nonweak selection on the Cartwheel graph.
In the limit as the hub-to-island weight ϵ goes to zero, the fixation probability for arbitrary mutant fitness r is expressed in closed form by Eq (17). Temperature and uniform initialization are equivalent in this limit. Dashed lines show the weak-selection approximation, with slope ρ′ given by Eq (19). (A) Fixation probability is plotted against r for two Cartwheels of size 12. CW4,2,4 has h > m and is therefore an amplifier of weak selection. CW2,5,2 has h < m and is therefore a suppressor of weak selection (but appears to amplify selection for r > 2.4219). Cartwheels with h = m have the same fixation probability as the well-mixed population, for all r, in the ϵ → 0 limit. (B) In the limits ϵ → 0 and n = h → ∞, with m = 2, the fixation probability jumps discontinuously from 0 to 1/3 as r crosses 1; the expression for r > 1 is given in Eq (20). For comparison we also show the upper bound ρ(r) ≤ 1 − (r + 1)−1, derived by Pavlogiannis et al. [8], which applies to all weighted graphs with no self-loops under temperature initialization.