Proton-Coupled Electron Transfer Guidelines, Fair and Square

Abstract

Proton-coupled electron transfer (PCET) reactions are fundamental to energy transformation reactions in natural and artificial systems and are increasingly recognized in areas such as catalysis and synthetic chemistry. The interdependence of proton and electron transfer brings a mechanistic richness of reactivity, including various sequential and concerted mechanisms. Delineating between different PCET mechanisms and understanding why a particular mechanism dominates are crucial for the design and optimization of reactions that use PCET. This Perspective provides practical guidelines for how to discern between sequential and concerted mechanisms based on interpretations of thermodynamic data with temperature-, pressure-, and isotope-dependent kinetics. We present new PCET-zone diagrams that show how a mechanism can switch or even be eliminated by varying the thermodynamic (ΔG_PT^° and ΔG_ET) and coupling strengths for a PCET system. We discuss the appropriateness of asynchronous concerted PCET to rationalize observations in organic reactions, and the distinction between hydrogen atom transfer and other concerted PCET reactions. Contemporary issues and future prospects in PCET research are discussed.

Introduction

“Life is nothing but an electron looking for a place to rest.” ¹ To this quote, attributed to the 1937 Nobel Laureate Albert Szent-Györgyi, we would add, “...with the help of a proton.” In a redox process, coupling the movement of a proton to an electron can impart an energetic advantage over solo electron transfer by lowering the activation barrier and the driving force of the reaction. Over the past two decades the scope and number of redox reactions recognized as being proton-coupled have increased dramatically. For example, proton-coupled electron transfer (PCET) reactions have been observed in inorganic, materials, organic, organometallic, and biological systems with the involvement of C–H, N–H, O–H, S–H, and M–H bonds (M = metal), Figure 1.²⁻⁶ With proton-coupled electron transfer lurking in so many reactions that scientists study, it behooves us to be able to identify the presence of PCET and mechanism(s) by which the reaction proceeds. In doing so we unlock the possibility to control PCET to improve kinetics and thermodynamics by reducing reaction barriers. The main PCET mechanisms are shown in square schemes, similar to Figure 2, which have become signature representations of PCET.

Figure 1.

Examples of PCET reactions range from (A) the long-range coupling of ET and PT in hydrogenases⁷ and (B) biomimetic PT wires⁸ to (C) water oxidation on metal oxides⁹ and (D) (photo)redox catalysis by PCET activation.¹⁰ Images were adapted from the original referenced papers: (A) copyright American Association for the Advancement of Science, 2020; (B–D) copyright American Chemical Society, 2018, 2011, and 2013, respectively.

Figure 2.

(Left) Square scheme that summarizes the mechanisms by which proton-coupled electron transfer can proceed. The edges of the square show the sequential mechanisms with ETPT and PTET on the top and bottom, respectively. The pathway bisecting the square is concerted, where e^– and H⁺ are transferred without the formation of an intermediate species. Note that the donor and acceptor units for ET and PT can be the same or different species. (Right) Illustration of the three main mechanisms for PCET, each with a distinct transition state.

In this Perspective we aim to (1) align readers with the current theoretical framework of PCET, (2) outline experimental methods to identify PCET mechanisms, and (3) give insight into how to predict and control PCET rates and mechanisms by design. The essential concepts from electron and proton transfer theories are described to set the stage for proton-coupled electron transfer theory. Strategies for delineation of PCET mechanisms are given along with guidelines on how predict and switch between different mechanistic regimes, as illustrated by experimental examples and zone diagrams.

1. Why Are Electron Transfer and Proton Transfer Coupled?

The origin of the coupling between electron transfer (ET) and proton transfer (PT) is energetic, but the coupling between these reactions will have a strong kinetic influence, as we will see below. For a PCET reactant, the reduction potential shifts upon protonation/deprotonation (ΔE°)—the greater the shift, the stronger is the coupling. This leads to a corresponding difference in pK_a values for the oxidized and reduced species, ΔE° = 0.059·ΔpK_a at 298 K, which corresponds to the Nernstian slope for the apparent potential of a pH-dependent 1e^–/1H⁺ process in Pourbaix diagrams. An example is shown in Figure 3 for a phenol derivative in water.

Figure 3.

(Left) Square scheme for phenol oxidation. Approximate E° and pK_a values in water, vs NHE, are given. (Right) Pourbaix diagram for a tyrosine derivative in water, adapted from ref (8), copyright American Chemical Society, 2005.

Large values of ΔE° and ΔpK_a reveal a strong interaction of the electron and proton being transferred. One contribution is the electrostatic effect on the environment from these charged particles, related to the Born energy (self-energy) of an ion in a dielectric medium,¹¹eq 1, where z is the ion valency, a the ionic radius, e the elementary charge, ε₀ the vacuum permittivity, and ε_r the solvent dielectric constant. Oxidation of a neutral species (PhOH) creates a charge, while a proton-coupled oxidation can be charge neutral. A charge-neutral reaction is energetically favorable, in particular in low-polarity solvents and hydrophobic parts of proteins where the Born energy would be large. In multi-redox reactions, coupled (de)protonations may avoid charge build-up that would make each successive redox step increasingly difficult. One example is proton-coupled oxidation of water oxidation catalysts that allows for several oxidation steps in a narrow potential range.^12,13 Another contribution to large ΔE° and ΔpK_a values is the electronic structure of the reactant itself. Already from the Lewis structures of, e.g., phenol and phenoxyl radical in Figure 4, it is clear that the electron density between the oxygen and hydrogen is strongly decreased upon phenol oxidation, which leads to a large ΔpK_a. Similar qualitative guidelines can be used to find other PCET reactants with a large electron–proton coupling.

1

Figure 4.

Lewis structure of phenol and the resonance structures of phenoxyl radical.

Large ΔE° and ΔpK_a values mean that ET and PT will be coupled over large pH and potential intervals (Figure 3). This means that there is a greater chance to find conditions where the reaction is concerted electron–proton transfer (CEPT), in which the electron and proton are transferred in one kinetic step, via a common transition state (k_CEPT in Figure 2). In the sequential mechanism, either PT or ET occurs first, creating a distinct but typically short-lived intermediate, before proceeding to the final product. The energetic coupling between ET and PT, and the mechanism the reaction follows, greatly impact the observed reaction rates and kinetic dependencies. With a short-lived intermediate, a steady-state approximation gives the usual limiting cases. When the reverse of the first step is much faster than the second step (k_–ET1 ≫ k_PT2, Figure 2), the observed rate constant is proportional to the equilibrium constant for the first reaction step (pre-equilibrium kinetics):

2

3

If the reverse of the first step is instead much slower than the second step (i.e., k_–ET1 ≪ k_PT2), the first step becomes rate-limiting:

4

5

Rate constant expressions for the ET, PT, and CEPT steps are given below for unimolecular reactions. For bimolecular reactions, the usual diffusional steps have to be included.^14,15

Below, we outline the energetic dependencies of the different PCET mechanisms and how those determine which dominates the reaction.

2. Theories of Electron and Proton Transfer Square Up for PCET

Electron and proton transfer theories have existed for decades and are quite extensive.¹⁴⁻¹⁹ The most well-recognized theory to reconcile coupled proton and electron transfer has largely been developed by Hammes-Schiffer and co-workers.²⁰⁻²² We provide a condensed description of the essential aspects in each theory and suggest further reading in the references provided.

2.1. Electron Transfer Theory

For nearly seven decades, Marcus theory has been instrumental for interpreting and predicting kinetics of electron transfer reactions.^14,16 In this theory electron transfer systems are well represented by harmonic free energy curves for reactant (R) and product (P) states, Figure 5. The nuclear coordinate includes the electron donor and acceptor and the surrounding solvent. The R and P curves capture the free energies of the donor/acceptor system when the nuclear coordinates are distorted from equilibrium and depend on the reorganization energy, λ, and ΔG_ET^°. λ is the change in energy when the equilibrium reactant state distorts to the nuclear coordinates of the product without transferring an electron, and ΔG_ET, the Gibbs free energy, is the energy difference between R and P at equilibrium coordinates. In the classical treatment, the reactant coordinate fluctuates away from the equilibrium position to an energy equivalent to the product state, where R and P intersect. The electron transfers from R to P, and the product nuclear configuration can then relax to equilibrium position at the minimum of P.

Figure 5.

(Left) Free energy parabolas for the reactant and product states along the nuclear coordinate for ET. (Right) Electron potentials for R and P states. At the intersection region the energies of donor and acceptor states are equal (dashed line) and the electron can tunnel through the barrier. From ref (23), copyright Uppsala University, 2010.

Electron transfer from R to P occurs by tunneling from nuclear configurations when R and P have equivalent energy. Nuclear coordinates appear static because the electron tunnels on the femtosecond time scale; the potential energy remains constant because the apparently frozen nuclei do not produce a change in kinetic energy, which satisfies conservation of energy. Electron tunneling can also occur below the intersection region if there is significant overlap between vibrational modes of reactant and product for nuclear tunneling.²⁴ These vibrational modes must significantly contribute to the reaction coordinate. This effect is most important at low temperatures and in the inverted region (below).

Equation 6 is the semi-classical, high-temperature expression for the rate constant of non-adiabatic electron transfer (k_ET) as a function of electronic coupling (V_el), λ, and reaction Gibbs free energy, ΔG_ET^°. The V_el term arises from the quantum mechanical coupling of reactant and product states at equilibrium. Rates of electron transfer are predicted to increase as −ΔG_ET approaches λ and reach a maximum when −ΔG_ET^° = λ. When −ΔG_ET increases beyond λ, the rate of electron transfer is, counterintuitively, predicted to decrease in what is called the Marcus inverted region. After decades of controversy, experimental evidence showed the predicted bell-shaped free-energy dependence of ln k_ET.²⁵ The decrease in k_ET in the inverted region was shallower than predicted from eq 6, due to contributions from nuclear tunneling to higher vibronic product states. This general free-energy dependence has been established in many more electron transfer systems since then.

6

2.2. Proton Transfer Theory

Quantum mechanical formulations for proton transfer theory are similar to descriptions of electron transfer.^18,19 In the strong coupling limit, the classical description of proton transfer may be sufficient. In the weak coupling, non-adiabatic limit, the proton is treated quantum mechanically and must tunnel to the product state. The rate constant expression for proton transfer (under certain limits) is analogous to eq 6, where k_PT depends on the reaction free energy, proton coupling, and reorganization energy.¹⁸ Reactant and product free energies along the nuclear (reaction) coordinate are well described by harmonic potentials as in ET.

Protons have a much greater mass than electrons, which results in proton vibrational wavefunctions that are significantly more localized. This greater localization restricts the proton to tunneling distances typically less than ∼1 Å.²⁶ Electron wavefunctions are relatively more delocalized and allow tunneling over tens of Å.²⁷ Vibrational wavefunctions tail-off exponentially, which means that a small increase in the proton tunneling distance can significantly reduce the proton wavefunction overlap. Proton tunneling is then predicted to have a much steeper distance dependence when compared to electron tunneling. Contraction (or expansion) along the proton transfer coordinate, r_PT, by molecular vibrations varies the proton wavefunction overlap to modulate the proton tunneling probability.

Compared to a proton, deuterons have a twofold mass, leading to more localized vibrational wavefunctions and smaller spacing between energy levels. The narrower spacing in deuteron quantum levels tends to increase the population of excited vibrational states, which are more delocalized than the ground state, while more localized wavefunctions tend to decrease the vibrational wavefunction overlap, relative to protons. These differences in proton versus deuteron wavefunction overlap—and by extension proton versus deuteron tunneling probabilities—are the physical origin of the kinetic isotope effect (KIE), where KIE = k_PT(H)/k_PT(D).²⁶ Considering only the ground vibrational states, KIEs significantly greater than 1 are predicted. However, excited vibrational states and contractions along the PT coordinate could result in isotope effects close to or even <1. The KIE can inform when a proton transfer is involved in the rate-limiting step of a PCET reaction (with caution, section 3.2). There is no way to determine the proton wavefunctions nor their overlaps experimentally, but computational methods can be used to predict the wavefunctions, their overlaps, and the extent to which each excited vibrational state contributes to PT.^28,29

2.3. Proton-Coupled Electron Transfer Theory

Many reactions that would traditionally be termed hydrogen atom transfer (HAT) have been found to occur by CEPT. HAT is a sub-class of CEPT reactions, and the distinction is not always trivial. If an R–H bond is oxidized by separate acceptors for the proton and electron (often termed “multi-site” ⁸ or “bidirectional” ^12,30 CEPT), the reaction is clearly not HAT, but it could still be CEPT.³¹ Even when the electron and proton are transferred to the same site, however, the reaction may still not be HAT. The phenol/phenoxyl PCET self-exchange has been classified as CEPT that is not HAT, because the proton is added to a σ-bond, while the electron is added to the π-system.³² This is in contrast to the HAT reaction of toluene/benzyl self-exchange, where both particles are added to the σ-bond. Another distinction focuses on the degree of electron–proton non-adiabaticity but leads to the same results for the two reactions just mentioned: HAT is an adiabatic reaction, and the electronic wavefunction varies smoothly with proton coordinate, while for non-adiabatic CEPT the wavefunction changes abruptly.³³ It has been pointed out that the HAT reactions do not involve significant charge redistributions, and a Marcus-type description with solvent polarization as reaction coordinate may therefore not be useful for HAT reactions.³³ The distinction between these mechanisms is not only theoretically important but may also manifest in, e.g., very different KIEs and solvent dependencies.

In CEPT, the electron and proton tunnel to the product state via the same transition state without the formation of intermediates (Figure 2). CEPT can be described as a vibronic transition between reactant and product states (Figure 6) where the transferring electron and proton are treated quantum mechanically and the other reactant nuclei and solvent are treated classically. In the high-temperature, non-adiabatic limit, the distance-dependent rate constant is described by eq 7.³⁴ Here μ and ν refer to donor and acceptor vibrational states, P_μ is the Boltzmann distribution of those states for the reactants, V_el is the electronic coupling constant, and S_μν (r_PT) is the distance-dependent Franck–Condon overlap between reactant and product proton vibrational wavefunctions.²⁸ The observed rate constant is the sum of all vibronic transitions (μ→ν) that result from the product of electronic coupling and proton wavefunction overlap.

7

Figure 6.

(Left) Free energy parabolas for the reactants and products as a function of reaction coordinate of a CEPT reaction. (Right) Schematic proton potentials (tunneling coordinate) for the reactants (A), transition state (B), and products (C) (potentials illustrate an electronically adiabatic case, with a single potential surface). From ref (23), copyright Uppsala University, 2010.

Both V_el and S_μν (r_PT) depend on the donor and acceptor distance. Electron wavefunctions are more delocalized than proton wavefunctions, which means that the tunneling event for the proton will be significantly more spatially restricted. Case in point, electrons have been observed to tunnel over very long distances, tens of Å, while protons typically tunnel over distances less than 1 Å, as discussed for PT above. As a consequence, even small modulations of the proton tunneling distance can significantly impact the rate of CEPT. S_μν(r_PT) can be approximated to decrease exponentially as the proton tunneling distance (r_PT) increases:

where r_PT,0 and S_μν(r_PT,0) refer to equilibrium values for the proton tunneling distance and Franck–Condon overlap, respectively, and β is the attenuation parameter. When ground-state vibrational wavefunctions make the dominant contribution, β values on the order of 25 Å^–1 or greater are predicted.^14,15,18 The distribution of P_μ to higher lying excited states can decrease β by increasing S_μν(r_PT) for longer tunneling distances. Anharmonic distortion of the proton potential lowers the energy of excited proton vibrational states and makes their wavefunctions more delocalized, which can lead to increased wavefunction overlap in the tunneling region. Very clear examples of this effect are demonstrated from calculations of the proton potentials in the references provided.^28,35

The proton tunneling distance dependence has been probed experimentally for three different series of phenolic compounds bearing an intramolecular nitrogen base, Figure 7.³⁶⁻³⁸ In all three series the PCET mechanism was found to be concerted, but attenuation of k_CEPT as a function of the distance gave very different β values: ∼0 (A), 27 (B), and 8–9 Å^–1 (C). The rather different attenuation in rates observed points to a key challenge in the study of real systems: it is extremely difficult to stringently isolate the proton tunneling distance as a variable in a series of molecules. Altering the composition between donor and acceptor units will also bring about changes in the electronic structure of the system that manifest in changes to pK_a and E°. For example, ΔE° was varied by ca. 120 and 200 mV in series A and B, respectively, while series C, with homologous proton donors and acceptors, still had ΔE° = 26 mV. Altering r_PT by molecular design can also change the degree to which excited vibronic states contribute to CEPT. Small structural changes can lead to significant anharmonic distortion of excited proton vibrational wavefunctions that increases S_μν(r_PT) to produce small β values. Demonstrative figures based on calculations of the proton potentials are given in ref (35). The three separate studies show that the proton tunneling distance dependence is a difficult parameter to generalize, even for systems that are structurally very similar.

Figure 7.

(A) Compounds for studies of PT distance dependence for CEPT, where Δr_O··N is the range of O–N distances within each series. (B) Data and linear fits for series C with two different oxidants.

The predicted trend in k_CEPT as the reaction free energy for CEPT (−ΔG_CEPT^°) is varied should show the same bell-shaped dependence as ET reactions; eq 8 is the derivative of ln k with respect to −ΔG_PCET in eq 6. Such a trend had, until recently, lacked experimental observation for CEPT reactions. Instead, several studies have shown a linear increase in k_CEPT with −ΔG_CEPT^°, with a slope α ≈ 0.4–0.5, in agreement with eqs 8 and 9 at low driving force. The expected curvature as the range of driving forces is extended has rarely been seen. This has explicitly or implicitly been explained by a large λ, so that a clear curvature would not be obvious, but in some cases the range of ΔG_CEPT has exceeded 1 eV (see section 3.5). One study of phenol-base compounds suggested some curvature of the ln k versus ΔG_CEPT^° plots as the driving force became large.³⁹

8

9a

9b

9c

The bell-shaped free-energy dependence of each vibronic transition could be concealed by multiple transitions. One study of tyrosine oxidation found a slope α = 0.6 in the plot of RT ln k vs −ΔG_CEPT^° when either the oxidant or base strength was varied, instead of 0.5 as in eqs 8 and 9 at ΔG_CEPT ≈ 0.⁴⁰ The authors suggested this as evidence for contributions from higher vibronic transitions. Slopes both much higher and lower than 0.5, however, have been reported for CEPT, and alternative explanations have been suggested (section 3.5).

It has been suggested that the effect of higher vibronic transitions would be so large for CEPT reactions that an inverted region is not likely to be observed.²⁸ This is because of stronger vibronic coupling for CEPT than for the typical medium-frequency C–C bonds involved in vibronic ET reactions. Nevertheless, an inverted region behavior for CEPT was recently reported for the first time, in photochemical charge recombination (Figure 8).²⁹ An explanation was provided that, due to the strongly anharmonic proton potentials, (near) activation-less transitions to higher proton vibrational states of the product were disfavored by negligible wavefunction overlap.^29,41 This demonstration is of fundamental importance and may aid the design of long-lived charge-separated states of PCET reactions.

Figure 8.

(Top) Structure and (bottom) free-energy dependence for photoinduced CEPT in anthracene–phenol–pyridine molecules. The blue (charge separation) and red (charge recombination) regions indicate qualitative free-energy dependences according to eqs 6 and 7, for three different solvents with different λ. Bottom panel reprinted from ref (25), copyright American Association for the Advancement of Science, 2019.

3. How to Determine the PCET Mechanism

In spite of its fundamental importance, it is often not simple to determine the mechanism of a PCET reaction, specifically if it is CEPT, ETPT, or PTET. With computational methods, many parameters would have to go into such calculations to compare predicted rate constants of sequential and concerted mechanisms. Experimental determination is also challenging, and in this section we discuss the different methods and arguments that can be used.

3.1. Using Thermodynamic Exclusionary Arguments

The absence of a detectable intermediate of sequential mechanisms is not proof of a concerted reaction, as intermediates are typically short-lived and never accumulate to a detectable degree. Thermodynamic exclusion arguments against the sequential mechanisms are often used instead. The differences in E° and pK_a between donor and acceptor are used to calculate ΔG° for the first step, and the calculated rate constant (eqs 2–5) is compared with the experimental one. For example, oxidation of a phenol with pendant base by a triarylammonium radical had an observed rate constant k_obs = 1 × 10⁵ M^–1 s^–1.⁴² For the first step of an ETPT, ΔG_ET^° = +0.71 eV, i.e., 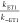≈ 10^–12. If rate-limiting ET would occur, k_ET1 = k_obs, and k_obs = 1 × 10⁵ M^–1 s^–1 would require that k_–ET1 ≈ 10¹⁷ M^–1 s^–1, which is many orders of magnitude faster than diffusion-controlled. Pre-equilibrium ETPT would require a similarly unphysical value for k_PT2, leading to the conclusion that the PCET mechanism was concerted.⁴² This approach relies on good E° and pK_a values, which are not always available. Moreover, these values are often taken from the separate reactants, and the relative values may change in the PCET reaction. In particular, the difference in pK_a of the separate proton donor and acceptor groups may change when they form a hydrogen bond. This is exemplified by both salicylate and bimolecular phenol-carboxylate complexes in acetonitrile, where the PT equilibrium constant can be as large as ∼0.1,⁴³⁻⁴⁶ in spite of the large ΔpK_a’s for benzoic acid (21.5) and phenol (29).^45,47

3.2. Kinetic Isotope Effects

The kinetic isotope effect, KIE = k_PCET(H)/k_PCET(D), compares PCET rates where a proton or deuteron is transferred. KIEs are often used to assign the mechanism, but this should be done with caution. k_CEPT depends on the overlap of the proton wavefunctions, which is typically smaller for the heavier deuteron, and a sizable KIE can be expected. Indeed, a “colossal” value of KIE = 455 was reported for the PCET reduction of benzoquinone by an Os(IV)–hydrazido complex in water.⁴⁸ Another well-known example is soybean lipoxygenase with a wild-type KIE = 81,⁴⁹ assigned to a non-adiabatic CEPT reaction.⁵⁰ These large numbers make mechanistic assignment safe. In most cases the situation is not that straightforward. First, a KIE can be expected also for a PTET mechanism, as it may involve proton tunneling. Second, there are several examples of even pure ET reactions with KIEs in the range of 1–2.⁵¹ When the reaction is carried out in protic solvent, the solvent usually has to be deuterated, which may affect the ET rate. In addition, the subsequent PT step of ETPT_pre-eq can give a KIE for the observed rate constant. Finally, many concerted PCET reactions show KIE values close to unity, as verified both computationally and experimentally.^28,29,38

At least two effects can explain a KIE ≈ 1 for CEPT. First, the proton transfer potentials are in many cases much less harmonic than a Morse potential. This lowers the energy of excited proton vibrational states and makes their wavefunctions more delocalized, and therefore more likely to contribute to the rate.^28,36 The second effect is the thermal distribution of tunneling distances that favors tunneling at PT distances much shorter than r_PT,0. Both effects are more important for deuterons, which reduces the difference in tunneling probability between H and D. Without these effects, very large KIEs would be common for CEPT.

KIEs that vary systematically with changes in driving force are often used to discuss the mechanism. In a typical example, the excited-state quenching of *[Ru((CF₃)₂bpy)₃]²⁺ ((CF₃)₂bpy = 4,4′-CF₃-2,2′-bipyridine) by a series of para-substituted phenols was studied in acetonitrile, in the presence of pyridine as proton acceptor.⁵² Five of the six phenols followed a free-energy dependence expected for CEPT with a slope α ≈ 0.5. For four of them, the KIE was 1.9–4.0, consistent with a CEPT reaction. 4-CH₃O-phenol, with the lowest E° value, had KIE = 1.0, which may indicate a competing ETPT.

3.3. Temperature Dependence

Sequential and concerted mechanisms may show different activation energies. In practice, activation energies can be too similar for a clear conclusion to be drawn, and they are rarely used to distinguish mechanisms.⁴² An exception is cases where the sequential reaction has a strongly endergonic first step, with ΔG° larger than the experimentally observed activation energy. The temperature dependence is instead often used to provide insight into vibronic effects of CEPT reactions in enzymes and small-molecule systems.^49,53−56 In eq 7, a temperature dependence of k_CEPT can be expected from mainly three factors: the Boltzmann population of reactant proton vibrational states (P_μ), the thermal distribution of proton tunneling distances (S_μν(r_PT)), and the classical barriers ΔG_μν^* = ) for the vibronic transitions. Disentangling the different contributions to the temperature dependence is difficult, but a combination of rate constants and KIEs as a function of temperature may provide sufficient input for data fitting or computational modeling. A larger experimental activation energy with deuterons may lead to inversion of KIEs at higher temperature, which can be interpreted in terms of compression along the PT coordinate to sample smaller r_PT values.^49,53−56 If the reactant proton potential is not too anharmonic, population of higher vibrational reactant states may be insignificant (P_μ≠0 ≈ 0), which offers some simplification.

3.4. Pressure Dependence

The reaction rate constant dependence on hydrostatic pressure has long been used to discuss reaction and activation volumes.⁵⁷⁻⁵⁹ For CEPT and HAT reactions in enzymes, an increase in pressure is expected to compress the enzyme, leading to shorter r_PT values, but many other parameters may change as well. For quantitative analysis, one approach has been to focus on the pressure-dependent KIEs, as all other changes in the reaction should cancel out.^50,53 For small-molecule ET in polar solvents, most of the pressure dependence is due to a volume decrease with increasing solvation, proportional to (ze)²/a (eq 1).⁶⁰ We know of only one systematic study of PCET in small molecules where pressure dependence was used to identify the mechanism: the oxidation of [(CpCH₂Py-R)(CO)₃WH] complexes by [Ru(bpy)₃]³⁺ derivatives (Py-R = pyridine base; section 4.3).⁶¹ It was found that k_PTET increased and k_ETPT decreased with increasing pressure, in agreement with predictions based on solvation changes. For PTET the zwitterionic [(CpCH₂PyH⁺-R(CO)₃W^–] intermediate solvation increased (volume decreased), while for ETPT the volume increase was due to the decrease in [Ru(bpy)₃]³⁺ solvation upon reduction. A volume decrease is expected for k_CEPT with increasing pressure, because [Ru(bpy)₃]³⁺ is also reduced in this reaction. Instead, an increase in k_CEPT was observed and attributed to the increased tunneling probability with pressure as r_PT decreased.

3.5. Driving Force Dependence

The driving force dependence of k_CPET is a very useful way to assign the mechanism, provided that a sufficiently large range of driving forces can be accessed with a homologous series of reactants with known relative ΔG° values. A plot of ln k_obs vs ΔG_ET^°, ΔG_PT, or ΔG_CEPT^° will result in very different slopes for the three mechanisms (sections 4.2 and 4.3). It is particularly interesting to examine CEPT reactions by comparing both variations in ΔG_ET and ΔG_PT^°. For tyrosine oxidation by M^III-polypyridine oxidants (M = Os, Ru, Fe) in buffers with different pK_a values, the dependence of ln k_PCET on ΔG_PT was quantitatively the same when the oxidant or buffer base strength was varied.⁴⁰ The same result was reported for oxidation of TEMPOH with a range of oxidants and pyridine bases, where a slope α = 0.46 was reported.⁶² A symmetric dependence was also reported for CEPT oxidation of [(Cp)(CO₃)WH] by Fe^III- and Ru^III-polypyridine oxidants and pyridine bases, with a slope α = 0.37.⁶³

A symmetric dependence of k_PCET on ΔG_PT^°, irrespective of whether oxidant or base is varied, is expected from the theory above, where both particles tunnel from a single transition state. Yet, there has been recent discussion of “asynchronous” transfer of electrons and protons to explain cases where the slope is much different from α = 0.5, and where α is different when the oxidant or the base is varied. In one interesting example, C–H activation by PCET was studied in a series of fluorenyl-benzoates with varying benzoate group pK_a values and a range of external oxidants.⁶⁴ The slope was α ≈ 0.20 when the oxidant was varied, but α ≈ 0.58 when the base was varied. This great difference was explained by an imbalanced (asynchronous) transition state that is late (more product-like) with the respect to the proton. Other studies of C—H, N—H, and C=O activation have also suggested asynchronous CEPT reactions, where the degree of progress for ET and PT at the transition state would be imbalanced.⁶⁵⁻⁶⁸ We have pointed out that this discussion is only valid when the transferring particle(s) is treated classically and is thus part of the reaction coordinate.⁶¹ In the non-adiabatic theory (eq 7), the reaction coordinate that defines the transition state involves only the heavy nuclear coordinates (including solvent). Both proton and electron tunnel between reactant and product states; consequently, there cannot be fractional transfer of either particle. It remains to be clarified if the asymmetric dependence observed can be explained with non-adiabatic tunneling or if, e.g., these systems require a classical description of the proton. Computational work has shown that the different slopes can be semi-quantitatively explained within the framework of eq 7 by differences in hydrogen bonding as the driving force is varied, which alters the wavefunction overlap.⁶⁹ It has also been suggested that the larger slope when the base was varied is because of a simultaneous PTET mechanism.⁷⁰

4. Factors Governing the Competition between PCET Mechanisms

As mentioned above, involvement of a CEPT mechanism can often only be shown by excluding the other alternatives based on kinetic arguments. In the following section, we try to illustrate the kinetic and thermodynamic factors governing the competition between PCET mechanisms.

Equations 2–5 give expressions for the rate constants of the two limiting cases of a sequential PCET mechanism: pre-equilibrium mechanisms and mechanisms limited by the initial reaction step. These are readily derived from a steady-state treatment of the reaction scheme of the PCET reactant (R) going through intermediate (I) to product (P), where k_obs denotes the observed PCET rate constant:

10

11

As the driving force for the initial step, −ΔG₁^°, increases, the elementary rate constant k_–1 decreases while k₁ increases. If the driving force for the first step can be varied independently of that of the second step, for example by varying the oxidant strength for an ETPT reaction, k₂ will remain constant. At large enough driving forces for the initial step, k_–1 ≪ k₂, and eq 11 simplifies to k_obs = k₁. The observed rate is then limited by the initial step, and the reaction is ET- or PT-limited. Regardless whether the first step is proton or electron transfer, its rate constant is generally well described by Marcus theory and takes the form of eq 6. At low driving forces for the initial step, k_–1 ≫ k₂, and eq 11 simplifies to k_obs = 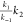= K_eq1k₂.

4.1. The Concerted Mechanism

The rate constant for a non-adiabatic CEPT reaction can be written in a form very similar to the Marcus expression for single charge transfer reactions (cf. eqs 6 and 7). Since CEPT makes use of the driving force for the total reaction, the activation barrier for a concerted step should be smaller compared to those for the initial ET or PT steps, which have smaller driving forces, unless the reorganization energy is much larger. The pre-exponential factor may be smaller than for ET and PT, however, because both the electron and proton have to tunnel.

4.2. The Driving Force Dependencies of Different Mechanisms

Each mechanism is expected to show a unique response to the combined changes in oxidant and base strength (ΔG_ET^° and ΔG_PT; Figure 9). Driving force dependence is therefore often the most valuable tool for mechanistic determination.

Figure 9.

Qualitative illustration of the different driving force dependencies for the sequential and concerted mechanisms when either ΔG_ET^° or ΔG_PT is varied. In each case, one of the rate-limiting mechanisms has a similar dependence as CEPT but lower driving force and larger vibronic coupling.

The rate constants of PCET reactions limited by either electron or proton transfer are expected to depend only on the driving force for the initial step, ΔG₁^°. Their rate constants are well described by Marcus-type formulations. The rate constant depends on driving force in the same way as for PCET in eq 8. In most cases of interest, the reaction will have a relatively low driving force compared to the reorganization energy of the reaction (|ΔG₁| ≪ λ₁), and the equation simplifies to

12

(i.e., α = 0.5 in eq 9). If the reaction instead follows a pre-equilibrium mechanism, the observed rate constant depends on the equilibrium constant of the initial reaction. This is related to the driving force by

13

As the subsequent step is independent of this change (i.e., k_PT2 would not change if ΔG_ET^° is varied), the driving force dependence of the observed rate constant becomes

14

(i.e., α = 1.0 in eq 9). It is therefore apparent that a pre-equilibrium mechanism will have a steeper dependence on the driving force of the initial step than if the rate constant is limited by this step. The second step of the sequential mechanism will be very exergonic and the overall rate most likely only weakly dependent on its driving force. These differences are qualitatively shown in Figure 9.

A CEPT mechanism makes use of the driving force for both steps. Although experimental exceptions have been reported (see section 3.5), PCET theory predicts that the CEPT rate constant changes to the same extent when the ET or PT driving force is varied. The expression for the dependence of the CEPT rate constant on driving force (eq 8) is analogous to that of single charge transfer events. However, as the reaction now makes use of the driving force of both steps, −ΔG_PCET^° is larger, and the term 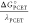cannot be neglected. The rate constant will therefore be somewhat less dependent on driving force:

15

(i.e., α < 0.5). Because of the weaker driving force dependence, CEPT is favored over sequential mechanisms by a low overall driving force when both −ΔG_ET^° and −ΔG_PT are small. In contrast, ETPT and PTET are favored by larger values of −ΔG_ET^° and −ΔG_PT, respectively.

4.3. Identifying and Switching between Mechanisms by Variations of Driving Force

Ru^II-polypyridine photosensitizers derivatized with tyrosine (Figure 10) were studied as model systems for the PCET reactions of Tyrosine_Z in Photosystem II.^71,72 The Ru^II complex was photo-oxidized by a laser flash in the presence of an external electron acceptor. We reported a concerted PCET mechanism for tyrosine oxidation by Ru^III in Ru_bpy-Tyr with proton transfer to water.⁷³ The reaction showed a weak pH dependence, with log(k_PCET) increasing by ca. 0.4 per pH unit, and a significant isotope effect, KIE = 3.0 ± 0.8.⁵¹ The reason for the weak pH dependence is not understood, but it seems characteristic for the CEPT reaction of related tyrosine and tryptophan systems under conditions where buffer and OH^– are not the primary proton acceptors. With the stronger oxidant in Ru_deeb-Tyr, the reaction at pH < 8 was instead pH-independent, with a smaller KIE = 2, which was assigned to an ETPT mechanism.⁵¹ This is consistent with the predictions above, that a strong oxidant favors ETPT. In Ru_bpy-Tyr with water (H₂O, OH^–) as primary proton acceptor, the mechanism switched from ETPT in the low-pH domain (A) via CEPT (B) to PTET (C) as pH increased (Figure 11).⁵¹ The ETPT reaction had an uphill first step, ΔG_ET^° = +0.16 eV. Thus, with the weaker oxidants Ru_dmb-Tyr and Ru_tmb-Tyr, the pH-independent ETPT was not observed, and the weakly pH-dependent reaction dominated also the low-pH region.

Figure 10.

Structures of the Ru-Tyr compounds.

Figure 11.

pH dependence of the rate constant for PCET oxidation of tyrosine in Ru_bpy-Tyr. The dominating mechanism was assigned to ETPT (A), CEPT (B), PTET (C), and ET from tyrosinate (D). Reprinted from ref (46), copyright American Chemical Society, 2012.

Tryptophan has a pK_a ≈ 17 in water that decreases to pK_a ≈ 4.5 upon oxidation, but E° for the uncoupled oxidation is ∼1.15 V vs NHE, ca. 0.25 V lower than for tyrosine, and tryptophan would be more prone to react via ETPT. The rate constant for Ru_bpy-Trp (analogue to Ru_bpy-Tyr) was pH-independent from pH 2.5 to 9, with KIE = 1.0 (Figure 12, red data).^74,75 The reaction at pH < 4.5 is pure ET to form the protonated radical product (λ_max = 570 nm). At pH = 4.5–9, the ET is followed by a slower deprotonation to the neutral radical (λ_max = 510 nm). The use of a weaker oxidant in Ru_tmb-Trp resulted in a weakly pH-dependent rate constant (as for Ru_bpy-Tyr) and KIE ≈ 3.5, which were assigned to a CEPT reaction (green data).

Figure 12.

pH dependence of tryptophan oxidation in Ru-Trp complexes analogous to the complexes in Figure 10: Ru_bpy-Trp (red), Ru_tmb-Trp (green), and the corresponding bromotryptophan complexes (dark and light blue). Reprinted from ref (75), copyright American Chemical Society, 2011.

In summary, the PCET mechanism in both the tyrosine and tryptophan complexes could be switched between CEPT and ETPT by varying the oxidant strength, although the changes in ΔG_ET^° and ΔG_CEPT are exactly parallel. This can be theoretically rationalized as explained in section 4.2 above.

Systematic studies on how to switch the PCET reaction mechanism have been experimentally undertaken using several different tungsten hydride (W-H) complexes, Figure 13. The first experimental evidence of concerted PCET in the oxidation of a metal hydride was reported for [(Cp)W(CO)₃H] (1).⁶³ The pK_a value of the W-H bond in 1 is 16.1 in acetonitrile, with a potential of +0.74 V vs Fc⁺/Fc for the one-electron oxidation step. Using a series of external pyridine bases with different pK_a values (from 9.6 to 14.2) and Fe^III-trisbipyridyl]³⁺ or [Ru^III-trisbipyridyl]³⁺ derivatives (4) as oxidants (E° = 0.36–0.73 V vs Fc⁺/Fc), the sequential reactions would have endergonic first steps. Nevertheless, with the strongest oxidant the mechanism was ETPT_lim, with an observed rate constant that was independent of pyridine. With the weaker oxidants and in the presence of external pyridine bases, the reaction instead followed a CEPT mechanism with rate constants depending on ΔG_CEPT^°, in agreement with eqs 8 and 9 (α = 0.37). The data for the two weakest oxidants fell on a common line, indicating that a change of ΔG_CEPT by variation of the oxidant or the base had the same effects on the rate.

Figure 13.

Structures of tungsten hydrides, oxidants, and bases.^61,63,76,77

More recently, a range of novel W-H complexes were synthesized (2), in which pyridyl groups were covalently linked to the cyclopentadienyl ring of the complex via a flexible methylene (CH₂) group.⁷⁶ The role of the pyridines as pendant proton relays was shown by a dramatic acceleration of the PCET reactions, compared to [(Cp)W(CO)₃H] reacting with the same external pyridine base and the same oxidant. An unexpected effect was that the stronger oxidants reacted via CEPT with complex 2 and the weaker bases, whereas the corresponding reactants with 1 and external pyridines reacted by ETPT_lim.⁶³ This is seen from Figure 14, where ln k_PCET is plotted versus the strength of the pyridine base: the blue line shows a slope according to eq 9 of α = 0.51, and KIE = 1.2–2.4, both in agreement with a CEPT reaction. Similarly, the weaker oxidants reacted via PTET (gray line, α = 1.03; KIE = 0.14–0.38), whereas the corresponding reactants with external pyridines reacted via CEPT. We suggested that the proton wavefunction overlap is somewhat better for the transition state of the covalently linked complexes 2 than for the bimolecular encounter complexes of 1, which would increase the probability for proton tunneling and favor CEPT and PTET. Further studies with even stronger, laser-flash-generated [Ru^III-trisbipyridyl]³⁺ oxidants (E⁰ = 0.82–1.03 V vs Fc⁺/Fc) showed an ETPT mechanism for 2a,b (α < 0.1, red dashed lines), but other mechanisms are similarly fast with the stronger bases.⁶¹ Also the dependence on E° was in good agreement with predictions (Figure 14). The inverse KIE (KIE < 1) is an equilibrium effect for PTET_pre-eq because of the difference in zero-point energy of the W-H and H⁺-pyridine vibrations. To summarize, compounds 2 were shown to undergo all three PCET mechanisms, depending in a systematic way on the variations in the oxidant and base strength. Their rate constants varied in agreement with predictions described above, which together with KIEs allowed for mechanistic assignment. The identification of a mechanism and its driving force dependence is important for design of, e.g., catalysts that operate with PCET in rate-determining steps. As is clear from Figure 14, the catalytic rate will show a dramatically different response to variations of ΔG_ET^° or ΔG_PT, or functional groups in the coordination environment, depending on which mechanism is followed.

Figure 14.

Second-order PCET rate constant for oxidation of the W-H compounds 2 by oxidants 4 versus pyridinium pK_a (top) and versus oxidant E° (bottom). (Top) The lines are linear fits to the data with the same oxidant: [Fe((OMe)₂bpy)₃]³⁺, α = 1.03 (gray line, PTET_pre-eq); [Ru(Me₂bpy)₃]³⁺, α = 0.51 (blue line, CEPT); and [Ru(bpy)₃]³⁺, α < 0.1 (orange dashed lines, ETPT). KIE values are given where measured. (Bottom) Linear fits for 2a–d ordered from low to high pK_a value. With the weaker bases (a, b), the mechanism changes from CEPT for oxidant E° = 0.50–0.73 (α = 0.41) to ETPT_pre-eq for E° = 0.73–0.9 (α = 1.03). With the stronger bases (c, d), the reaction was assigned to PTET_pre-eq with a weak dependence on E° (α ≈ 0.08). At E° > 0.9 V, the initial ET is downhill, and the rate levels off. Reprinted from ref (61), copyright American Chemical Society, 2019.

Dempsey and co-workers⁷⁷ published a closely related study of PCET reactions of the tungsten hydride complex [(Cp)W(CO)₂(PMe₃)H] as a rapidly interconverting mixture⁷⁸ of 3-trans (58%) and 3-cis (42%) isomers. They covered a very similar range of ΔG_ET^° and ΔG_PT for their mechanistic study as for 1 above, and they also found that the mechanism changed between sequential and concerted, depending on driving force. An interesting difference compared to our studies is that CEPT gave at most a minor contribution to the observed rate for all conditions. They suggested that this was related to a larger reorganization energy for 3 than 1. We proposed instead that the differences are due to the steric effect of the bulky PMe₃ ligand, which would be stronger in the 3-cis isomer⁷⁸ and decrease the proton wavefunction overlap for CEPT. If our suggestion is correct, this would be an experimental illustration that the point of switching between ETPT and CEPT depends on S_μν(r_PT) (eq 7). Another experimental illustration may be the observation above that complexes 2, with a covalently linked pyridine, favor CEPT over ETPT compared to 1 and external pyridines.

4.4. Illustrating the Competition between Mechanisms with Zone Diagrams

The competition between PCET mechanisms is well illustrated by zone diagrams, showing which mechanism is operational at a given driving force for ET and PT. By giving each of the possible elementary steps a Marcus-type rate expression, eqs 6 and 7, and inserting driving forces for the individual steps, the rate constants for each mechanism can be calculated, and the dominant mechanism under given conditions be determined. Figure 15 shows such zone diagrams for an oxidative PCET reaction. Here, the y-axis shows the driving force for initial ET (ΔG_ET1^°, in eV), and the x-axis shows the driving force for initial PT (ΔG_PT1, as the difference in pK_a of the PCET reagent and the conjugate acid of the accepting base). For this example, the potentials for oxidation of the protonated and deprotonated species, as well as the pK_a values of the reduced and oxidized forms, are taken from a study of a previously reported tungsten hydride system.⁶¹ In this way, the effect of varying the relative pre-exponential factors for the rate constants of the elementary steps (indicative of electronic and vibronic couplings), or their reorganization energies, can be demonstrated. Table 1 summarizes the relative pre-exponential factors (A) and reorganization energies (λ) assumed in Figure 15. We note that these values are chosen arbitrarily for demonstrative purposes and do not refer to a specific reaction. Further description is given in the Supporting Information.

Figure 15.

Zone diagrams for oxidative PCET. Thermochemical data for these examples is taken from ref (76), and kinetic factors for the different scenarios are summarized in Table 1.

Table 1. Reorganization Energies (λ) and Relative Pre-exponential Factors (A) for the Kinetic Equations (see Supporting Information) of the Scenarios Described by Zone Diagrams in Figure 15.

	plot
	A		B		C		D
	λ (eV)	A (au)	λ (eV)	A (au)	λ (eV)	A (au)	λ (eV)	A (au)
kPT1	0.9	0.9	0.9	0.9	0.9	0.9	0.9	0.01
kET1	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0
kPT2	0.9	0.9	0.9	0.9	0.9	0.9	0.9	0.9
kET2	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0
kCEPT	1.65	0.01	1.65	0.001	1.65	0.0001	1.65	0.0001

The diagrams visualize how the prevalence of a CEPT region depends on the vibronic coupling. In the scenario described by Figure 15A, at high driving forces for either ET or PT, the reaction proceeds through sequential mechanisms. At moderate driving forces for both, the reaction proceeds through CEPT. As the pre-exponential factor for CEPT decreases relative to those of the individual ET and PT reactions (Figure 15B), the CEPT zone shrinks and splits into two regions. In a system where the coupling is small, due to, for example, an elongated, sterically hindered hydrogen bond, a CEPT region may exist only in a narrow driving force window or may not occur at all (Figure 15C). This provides an explanation for the lack of a dominant CEPT pathway from complex 3, where the PT coordinate is obstructed by the bulky PMe₃ ligand (see above).

As the relative pre-exponential factor for CEPT decreases, for example, by increasing the proton transfer distance, the pre-exponential factor for initial PT can also be expected to change. This scenario is illustrated in Figure 15D, where all factors are the same as in Figure 15C except the pre-exponential factor for initial PT, which is smaller. In this case, the initial PT step is slow enough to be outcompeted by CEPT with sufficiently large driving forces for ET. CEPT can, however, still not outcompete PTET in the pre-equilibrium regime, since the rate of pre-equilibrium PTET is not affected by the pre-exponential factor of the initial PT step (see eq 14).

Figure 15 illustrates what has previously been shown to be a key feature of CEPT reactions.⁶³ While strong oxidants or bases favor ETPT or PTET pathways, respectively, the concerted reaction may dominate when both ET and PT driving forces are small. The latter is therefore particularly attractive for energy-related applications in catalysis, as a low overall driving force means energy-efficient conditions. In addition, the zone diagrams show that low overall driving force is not a requirement for CEPT, which extends to the upper right corners of Figure 15. A balance in oxidant and base strength may lead to a concerted mechanism, even at relatively high driving forces for ET and PT.

5. The Future Is Looking Very Bright for PCET

For the past several centuries, humans have reaped the benefits of rationally designed chemical processes to bring a plethora of new chemicals (and technologies) that have been integrated into our daily way of life. Of the many synthetic processes that involve oxidative or reductive chemistry, strategies did not necessarily take advantage of benefits that can be gained from PCET. Examples of redox reactions that are coupled to proton transfer were known for many years before the term PCET was used; take, for example, the use of Pourbaix diagrams to track reduction potentials as a function of proton concentration, or the discovery that ATP synthase depends on a transmembrane proton gradient generated by PCET reactions. The notion to intentionally make the best use of coupled electron and proton transfer processes in rationally designed chemical systems is gaining momentum.⁷⁹ In many areas of science, there are new and exciting examples of PCET reactions and promising implementations. We highlight some of these areas below.

In organic synthesis, recent efforts have demonstrated the utility of using PCET as a strategy to homolytically activate X—H (X=S, N, O, C) and C=Y (e.g., Y=O) bonds by oxidative or reductive pathways, respectively.^4,80,81 For example, multi-site PCET has been used to overcome thermodynamic constraints that can be encountered when using H atom acceptors. In this way, the combined strength of the separate electron and proton acceptors can give much higher effective bond dissociation free energies (BDFEs) than even the strongest HAT acceptors.^4,82 Incorporating PCET as a synthetic strategy has also been shown to enable high yields and enantioselectivities in asymmetric coupling reactions.^80,83 Redox mediators are commonly used in electrochemical and photoelectrochemical systems. In a recent report, a new electrochemical PCET mediator based on electroactive cobaltocene functionalized with a proton-donating aniline was used to catalytically activate the C=O of acetophenone.⁶⁷ The mediation strategy prevented the electrocatalytic H₂ formation side reaction, which is a frequent issue encountered under reductive catalytic conditions. Meanwhile, new reactions proposed by synthetic chemists may give feedback to fundamental PCET research, raising questions like the distinctions between hydrogen atom transfer (HAT) and CEPT (section 2) and whether proton-coupled inner-sphere electron transfer can be described as PCET.⁸⁴⁻⁸⁶ In many studies, arguments based on models for proton tunneling in non-adiabatic CEPT (section 2) are frequently mixed with those based on classical models, discussing, e.g., polarization and/or asymmetry of the transition state based on Hammett plots or direct free-energy correlations (section 3.5).^64,67,68 An interesting development in PCET would be to harmonize the theoretical description behind the above phenomena.

The occurrence of PCET in many enzymes is widely recognized. For example, Nature has optimized strategies for the life-sustaining chemistry of catalytic carbon, nitrogen, and oxygen cycles. Enzyme efficacy is facilitated by specialized outer coordination spheres that supply reactants (e^–, H⁺, and substrate) to highly organized active sites that catalyze thermodynamically or kinetically challenging chemical transformations that would otherwise be impossible under terrestrial conditions. What we learn from PCET in enzymes and protein systems can be applied to rationally designed catalytic systems. One area of great potential impact is the development of efficient means to utilize solar energy to drive the catalytic conversion of stable molecules like water, carbon dioxide, or dinitrogen into storable fuels or chemical feedstocks. Coupling challenging redox reactions to proton transfer can reduce the overpotentials needed or increase the catalytic rate constants. Careful energetic matching of the reaction steps may impart catalytic reversibility, as demonstrated for CO₂/HCOO^– conversion.⁸⁷ An interesting strategy inspired by Nature is the use of a pendent proton donor to keep the proton transfer distance “under control” to enhance PCET rate constants. Such a strategy has already been successfully incorporated into some catalysts,⁸⁸⁻⁹³ but caution should be taken in assuming that proton relays are active players in PCET, because effects other than proton transfer (by shuttling) may be involved.

Biological PCET also shows strategies for coupled transport of electrons and protons, where electrons are transferred in long-range steps coupled to several short-range proton transfers along the same pathway, as in ribonucleotide reductase,⁹⁴ or along separate but coupled pathways, like in hydrogenases.⁷ An elegant, bioinspired example is a phenol derivative linked to a chain of benzimidazole units, forming a hydrogen-bonded proton wire: ET from the phenol unit is coupled to three-step PT reactions to the terminal proton acceptor.⁹⁵

An interesting subset of two-electron redox reactions in proteins involves electron bifurcation.^96,97 The electron bifurcator (e.g., hydroquinone or flavin) transfers two electrons, where one electron goes to a low-potential acceptor and the other to a high-potential acceptor. This appealing a strategy is yet to be reported in non-natural systems. Proton coupling of the bifurcator oxidation narrows the span of potentials for successive redox steps, and under the right conditions it leads to potential inversion.

Molecular models of PCET and multi-PCET catalysis are increasingly being used to discuss charge transfer reactions in metal oxides and heterogeneous catalysts. For example, interfacial charge transfer in metal oxide semiconductor nanoparticles is suggested to be coupled to proton transfer in a one-to-one stoichiometry, much like for small molecular complexes.² This contrasts with predictions from band theory of bulk semiconductors. Metal oxides, e.g., cobalt-, nickel- and manganese-oxide, are heterogeneous water oxidation electrocatalysts and have been described by molecularly detailed models; oxidation state changes of individual metal atoms and molecular kinetic models have been shown to involve PCET.^98,99 For CO₂ reduction at copper electrodes, both concerted and sequential PCET mechanisms have been identified, depending on conditions (e.g., pH),^39,100 which is different from the typical assumption that ET and PT at metal electrodes are always concerted. It was recently shown that a metallic electrochemical response at graphite electrodes was maintained upon the introduction of molecular catalytic sites.¹⁰¹ Imparting molecular control to a heterogeneous catalyst is an appealing new strategy to tune proton-coupled redox potentials and expand chemical reactivity.

Excited-state PCET reactions are mainly studied from thermally relaxed states, where the theories for ground-state PCET still apply, which then open for photochemically driven formation of ground-state PCET products (Figure 16).^102−104 These are in contrast to the typical excited-state intramolecular proton transfer reactions (ESIPT), where a (near) barrier-less PT forms an excited-state tautomer, which then decays to the ground state via a conical intersection.^105,106 Also “photo-EPT” has been suggested, where absorption of a photon leads to direct population of a CEPT product, in analogy to intervalence charge transfer transitions.¹⁰⁷ Theoretical analysis suggests that there may be sufficient proton vibrational wavefunction overlap in the Franck–Condon region for direct formation of the CEPT product state, with the proton in a position far from equilibrium.¹⁰⁸

Figure 16.

Electronic ground- and excited-state square schemes (cf. Figure 1) illustrating the different pathways of ground-state CEPT (orange arrow), excited-state CEPT (red arrow), ESIPT (blue arrow), and “photo-EPT” (purple arrow).

Many aspects of PCET call for further fundamental research. For instance, it is difficult to predict how k_CEPT will be affected by changing proton tunneling distance, as it has only been systematically tested in a very limited number of systems (section 2). Another phenomenon that warrants further inquiry is the asymmetric dependence on electron and proton driving forces in concerted reactions, the origin of which is under debate (section 3.5). Interestingly, the Marcus inverted region, which was at one time predicted not to be possible for CEPT reactions,¹⁰⁹ was first observed in a series of phenol-base model systems.²⁹ This research is just one example of how synthetic model systems can lead to new paradigms. Fundamental experimental studies in combination with computational methods are of key importance for advancing our knowledge of PCET, where more robust guidelines and predictive tools will allow for better rational design of systems that utilize PCET.

In his Nobel lecture, Rudolph A. Marcus noted that the field of electron transfer had grown enormously.¹¹⁰ He summarized schematically a sampling of the areas in which electron transfer had been reported. One of the boxes is labeled “coupled ET and proton transfer”, Figure 17. It is remarkable that in the nearly three decades since Marcus’ Nobel lecture, the field of PCET has also grown enormously, and it is exciting to see how PCET has permeated so many of the areas in the ET field. We hope that readers feel inspired to find connections between coupled ET and proton transfer and the other boxes in the diagram and, perhaps, to draw some new boxes of their own.

Figure 17.

Areas of chemistry involving electron transfer as described by Rudolph A. Marcus in his Nobel lecture (redrawn from the original).⁹⁶

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c09106.

• Construction of PCET zone diagrams (PDF)

Author Present Address

^⊥ T.L.: State Key Laboratory of Elemento-Organic Chemistry, College of Chemistry, Nankai University, Tianjin 300071, China

Author Contributions

^§ R.T. and T.L. contributed equally to this work.

The authors declare no competing financial interest.