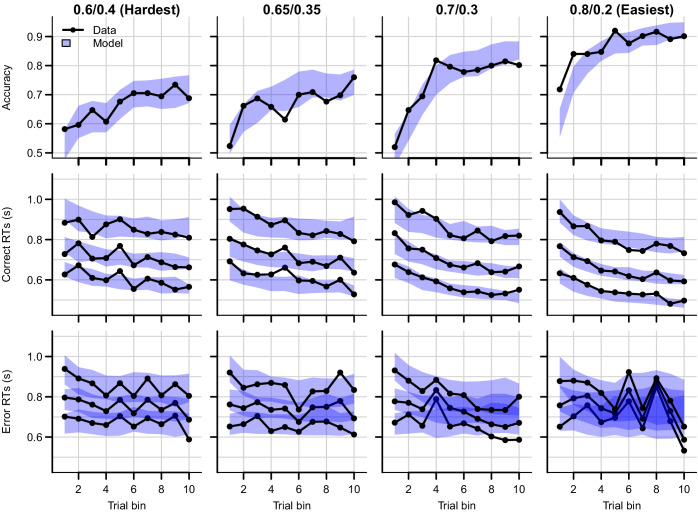
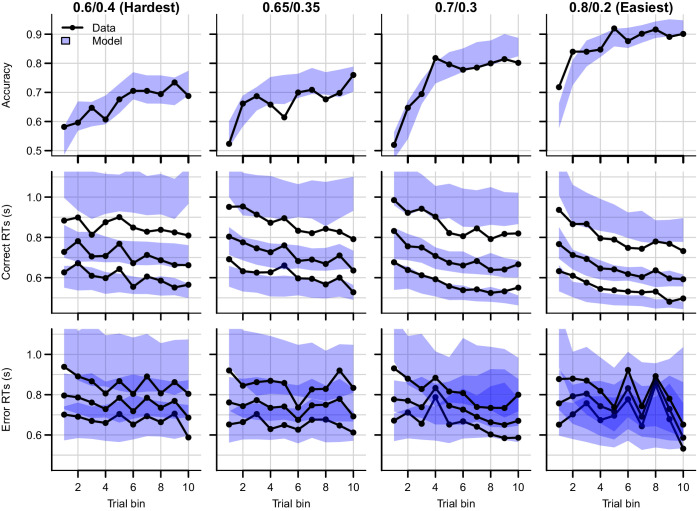
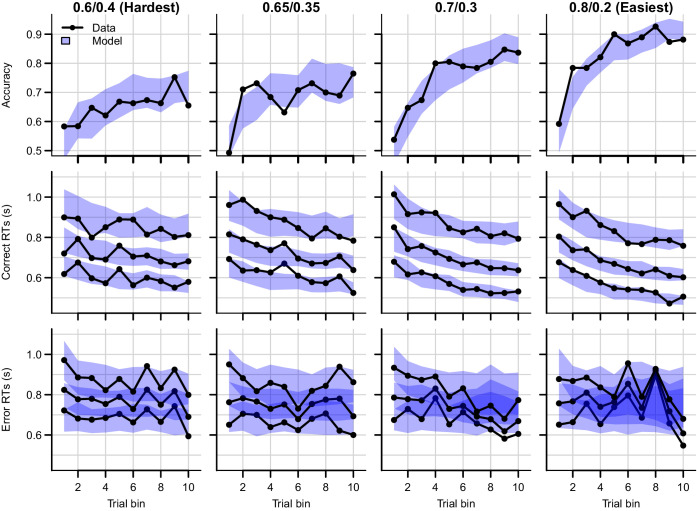
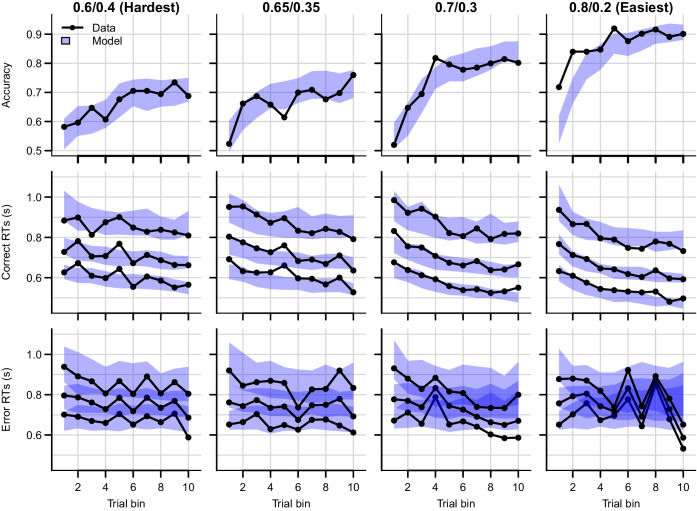
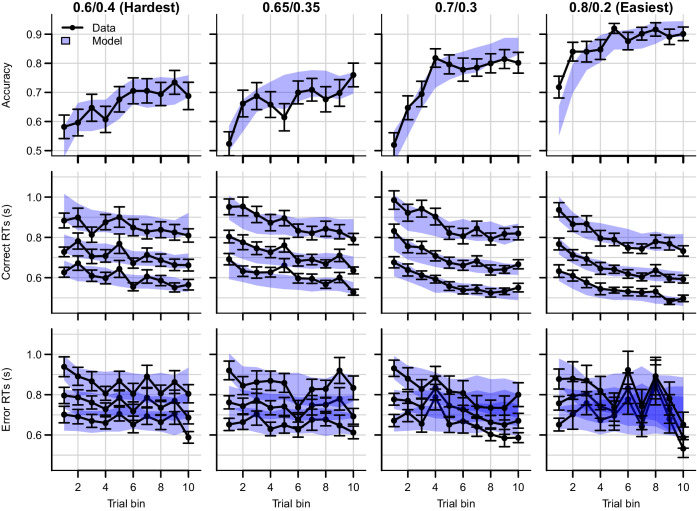
Figure 4. Data (black) and posterior predictive distribution of the RL-ARD (blue), separately for each difficulty condition.
Column titles indicate the reward probabilities, with 0.6/0.4 being the most difficult, and 0.8/0.2 the easiest condition. Top row depicts accuracy over trial bins. Middle and bottom rows show 10th, 50th, and 90th RT percentiles for the correct (middle row) and error (bottom row) response over trial bins. Shaded areas correspond to the 95% credible interval of the posterior predictive distributions. All data and fits are collapsed across participants.