Curvature processing in human visual cortical areas

Abstract

Curvature is one of many visual features shown to be important for visual perception. We recently showed that curvilinear features provide sufficient information for categorizing animate vs. inanimate objects, while rectilinear features do not (Zachariou et al., 2018). Results from our fMRI study in rhesus monkeys (Yue et al., 2014) have shed light on some of the neural substrates underlying curvature processing by revealing a network of visual cortical patches with a curvature response preference. However, it is unknown whether a similar network exists in human visual cortex. Thus, the current study was designed to investigate cortical areas with a preference for curvature in the human brain using fMRI at 7T. Consistent with our monkey fMRI results, we found a network of curvature preferring cortical patches—some of which overlapped well-known face-selective areas. Moreover, principal component analysis (PCA) using all visually-responsive voxels indicated that curvilinear features of visual stimuli were associated with specific retinotopic regions in visual cortex. Regions associated with positive curvilinear PC values encompassed the central visual field representation of early visual areas and the lateral surface of temporal cortex, while those associated with negative curvilinear PC values encompassed the peripheral visual field representation of early visual areas and the medial surface of temporal cortex. Thus, we found that broad areas of curvature preference, which encompassed face-selective areas, were bound by central visual field representations. Our results support the hypothesis that curvilinearity preference interacts with central-peripheral processing biases as primary features underlying the organization of temporal cortex topography in the adult human brain.

1. Introduction

In an attempt to elucidate the neural mechanisms by which high-level object representations are built, decades of research have been dedicated to understanding the visual features processed along the ventral visual pathway (e.g. Ungerleider and Mishkin, 1982; Bruce et al., 1981; Tanaka, 1996; Brincat and Connor, 2004; Tsao et al., 2006). For example, neurons in early visual areas (e.g. V1) respond strongly to simple, oriented edges (Hubel and Wiesel, 1959), while those in high-level visual areas respond to more complex visual stimuli, including faces (Bruce et al, 1981; Kobatake and Tanaka, 1994; Kanwisher et al., 1997; Tsao et al., 2006).

Curvature is one among many visual features that have been shown to be important for visual perception. Several studies have demonstrated that curvilinear features are significantly easier and faster to detect than rectilinear features (Treisman and Gelade, 1980; Wolfe et al., 1992; Kristjansson and Tse, 2001), suggesting that dedicated neuronal circuits might exist for curvature processing. In addition, children (Jadva et al., 2010; Amir et al., 2011) as young as 1-week old (Fantz and Miranda, 1975) look longer at curved stimuli than at rectilinear stimuli, indicating that a bias towards curvature processing emerges at a very early stage in development. Consistent with these human results, it has been found that nonhuman primates (Munar et al., 2015) also prefer curvilinear compared to rectilinear stimuli, suggesting that a bias towards curvature processing is conserved across primate species.

Recently, the results of our fMRI study in rhesus monkeys (Yue et al., 2014) have shed light on the neural machinery underlying curvature processing by demonstrating a network of visual cortical areas selective for curvature, which included three patches: a posterior curvature-preferring patch (PCP) located in dorsal V4, a middle curvature-preferring patch (MCP) located in the posterior superior temporal sulcus (STS) within area TEO, and an anterior curvature-preferring patch (ACP) located within anterior area TE just ventral to the STS. In addition, other studies (Srihasam et al., 2014; Arcaro and Livingstone, 2017) have found cortical areas with a preference for curvature processing extending from early visual areas to anterior inferior temporal (IT) cortex in both adult and infant monkeys. The results of these monkey studies thus provide neural evidence that there exists dedicated neural circuitry for curvature processing.

If curvature is a fundamental visual feature and its processing is conserved across primate species, we predicted that humans, like monkeys, would also have cortical areas with a preference for curvature processing. Further, we anticipated that such areas would most likely be found in regions of the ventral visual pathway, the pathway mediating object recognition. Thus, in the current study, we looked for curvilinear (and rectilinear) preferring areas in the human visual cortex using fMRI at 7T, and we compared these areas to those described in monkeys.

2. Materials and methods

2.1. Subjects

15 subjects (11 female, age range 22–40 years) participated in the fMRI experiment, 12 of whom (8 female, age range 22–40 years) underwent retinotopic mapping. All subjects had normal or corrected-to-normal vision. Informed consent was obtained from all subjects under a protocol approved by the Institutional Review Board of the National Institute of Mental Health.

2.2. Visual stimuli

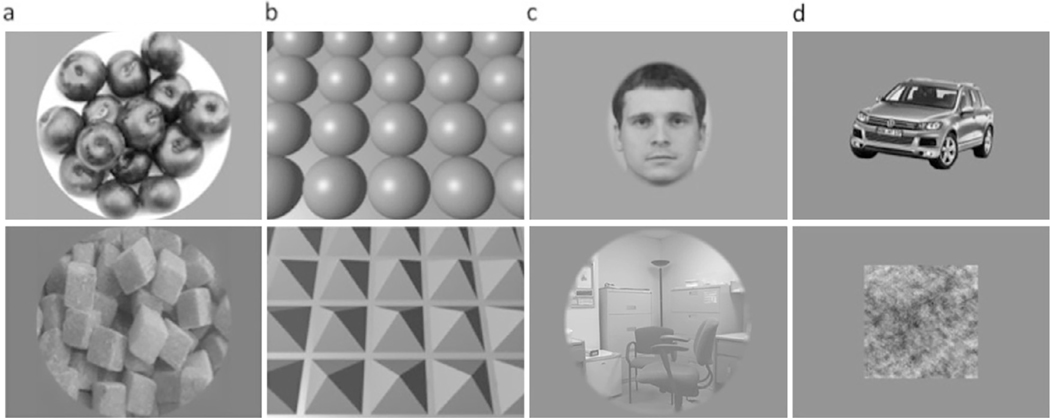
The experiment tested for the existence of areas in visual cortex with a significant preference for curvature. As shown in Fig. 1, there were 8 conditions, each with 8 exemplars: 1) round and 2) rectilinear natural or man-made objects; arrays of 3) spheres and 4) four-sided pyramids; conventional localizers for 5) faces, 6) scenes, and 7) man-made intact objects; and 8) Fourier scrambled objects. Rectilinear stimuli were chosen as a control for round stimuli because rectilinear stimuli lack curved contours and smooth surfaces, but (like circles and spheres) are also closed figures. The four-sided pyramids are essentially cubes, viewed from an atypical viewpoint and bisected by the common array plane. Differences in retinotopic footprint across conditions served specific purposes as noted below. To account for these differences in our experiment, we constrained the comparison of certain conditions.

Fig. 1.

Examples of stimuli: (a) round vs. rectilinear shapes; (b) computer-generated 3D spheres vs. pyramid arrays; (c) faces vs. scenes; (d) objects vs. scrambled objects.

Round and rectilinear object stimuli (conditions 1 and 2) were qualitatively chosen and downloaded from the internet (Fig. 1a). The images in conditions 1 and 2, composed of objects such as rings, grapes, and Rubik’s cubes, were presented within a circular aperture (diameter = 15˚) with equal mean luminance and root-mean-square (RMS) contrast. The round and rectilinear object stimuli included only natural or human-made inanimate objects to avoid confounding curvature response preference with the categorical animate-inanimate response (Long et al., 2017, 2018; Zachariou, et al., 2018).

The arrays of computer-generated shapes (conditions 3 and 4) were generated using Blender (Amsterdam, Netherlands) and spanned 20 × 15˚ (Fig. 1b). The arrays of computer-generated shapes covered the entire screen used for visual presentation, forming a rectangular aperture. This design was used to examine curvature response preference across as much of the visual field as possible. No face or scene images were included in the round and rectilinear objects or computer-generated shape conditions.

Face stimuli (condition 5) were created by encircling frontal view facial images taken from lab members in an oval shape. Images of the object stimuli were downloaded from the internet and included a wide range of common man-made objects, both curved and rectilinear. The original backgrounds of the objects were removed digitally using Photoshop (San Jose, CA) to generate isolated objects. To generate the scrambled objects, we transformed the intact objects into the Fourier domain and scrambled their phase spectrum while keeping the power spectrum intact, and then reversed the Fourier transform to get back to the image domain. The scrambled images were rectangular to preserve as much of the information in the original intact images as possible. The average sizes of the face, object, and scrambled object images were equated based on horizontal and vertical visual angle, which extended 8.4 × 10.0˚. Images of scenes were downloaded from the Internet and included indoor and outdoor scenes. These were presented within a circular aperture (diameter = 15˚).

2.3. Experimental design

We used a block design for the experiment in which blocks were presented in random order along with an alternating baseline of blocks with a uniform gray display. Eight images for every condition were presented for 1sec each, twice per block, in random order. Each run, including 8 blocks of stimuli on and 9 blocks of stimuli off, lasted 4 minutes 32 sec. Each subject was scanned with 8–10 runs in a single session. During the experiment, a dummy task was used to maintain the subjects’ attention during the course of scanning. The subjects were instructed to press a key to indicate a change in color of the fixation spot from blue to red, which occurred randomly and happened 20% of the time during a run.

The stimuli were projected onto a screen within the scanner bore, via an LCD projector (PLUS Corporation of America, 1024 × 768 pixels) using PsychToolbox (Brainard, 1997; Pelli, 1997).

2.4. Retinotopic mapping

We used horizontal and vertical checkerboard wedges to define the vertical and horizontal meridians across visual cortex and to identify the borders of retinotopically organized visual cortical areas. The checkerboard wedges extended 7.5 degrees from the fovea to 5 degrees in the periphery. The horizontal and vertical checkerboard wedges were presented in interleaving blocks for 16 seconds with 4 repeats of each condition per run. We collected 4 runs for each subject. During the scan, the subjects were instructed to press a key to indicate a change in color of the fixation spot from blue to red, which occurred randomly and happened 20% of the time during a run.

12 out of 15 subjects had their retinotopy mapped in a separate scan session. The remaining 3 subjects failed to show up for the retinotopy scan; therefore their retinotopy was defined by projecting the averaged retinotopy map generated from the 12 subjects onto their brains using sphere transformation (Fischl et al., 1999) to estimate the retinotopic borders.

2.5. Imaging acquisition: fMRI

Scanning was conducted in a Siemens 7T scanner, using a 32-channel surface coil. The EPI scan parameters were: TR = 2 s; TE = 14.29 ms; flip angle = 75˚; 28 slices, in-plane matrix size = 64 × 34. Voxel size was 1.4 mm isotropic. Five anatomical scans were also collected (TR = 6 s; TE = 2.99 ms; 0.75 mm isotropic; MP2RAGE) and then averaged to create the anatomical data used to create reliable cortical surfaces for each subject using FreeSurfer (http://surfer.nmr.mgh.harvard.edu).

2.6. Data processing: fMRI

2.6.1. Individual subject-level analysis

All functional data were preprocessed with motion correction and slice-timing correction in 3D volume space for each run separately. To increase registration accuracy between low-resolution functional data and high-resolution anatomical data (Fischl et al., 1999), the built-in FreeSurfer surface-based registration function, bbregister (Greve and Fischl, 2009), was employed to register the first functional image of each run to a high-resolution anatomical image of the same subject with six degrees of freedom. This surface-based registration algorithm created a registration matrix for each run. Using the registration matrices, we transformed the functional data to the high-resolution anatomical space of the same subject run by run, where the Freesurfer surface data (such as an inflated brain) exists. Functional data from all runs of an individual subject were thus transformed into the same individual’s FreeSurfer space. Statistical analysis of the functional data was performed only on gray matter, defined by FreeSurfer surface reconstruction. The surface-based functional data were spatially smoothed with a 2-mm Gaussian kernel for each run. Then, the surface-based functional data across all runs were concatenated for regression with a General Linear Model (GLM). Each condition was modeled as a convolution of a boxcar with a human hemodynamic response function. To reduce the influence of head movement, the three motion measurements generated from the 3D motion correction were included in the GLM fitting, in addition to the experimental conditions. These steps resulted in eight values for each voxel in the gray matter, with each value representing the percent signal change for a condition. Statistical analysis of individual subject-level functional data was conducted exclusively on surfaces.

2.6.2. Group-level random effects analysis

After preprocessing with motion correction and slice-timing correction, all 15 individual subjects’ data were resampled into the common FreeSurfer averaged brain surface space and then concatenated into a single file. Next, the GLM was applied to the single concatenated file to compute group-level random effects analysis by treating each subject as an individual data point. Multiple comparisons were corrected for, using a false discovery rate (FDR) of 0.05.

2.6.3. Defining ROIs

Face-selective areas :

We defined the occipital face area (OFA) and the fusiform face area (FFA) by contrasting the fMRI response to faces > objects, using group-level random effects analysis with the statistical threshold at FDR < 0.05. The individual subject-level face-selective areas were defined in their native space by the same contrast as was used in the group-level analysis. The size of ROI was defined on the surface in terms of number of vertices.

Scene-selective areas :

As scene stimuli had the same visual angles as curvilinear and rectilinear shapes, the scene-selective areas were defined using group-level random effects analysis with the statistical threshold at FDR < 0.05 on fMRI responses to scenes > curvilinear and rectilinear stimuli. These included the parahippocampal place area (PPA) and retrosplenial cortex (RSC). The individual subject-level scene selective areas were defined by the same contrast as that used in the group-level analysis.

2.7. Quantifying image curvature

We modified the method used in Yue et al. (2014) to quantify curvilinear information present in visual stimuli. After normalizing the mean luminance and root-mean-square contrast of the stimuli, we calculated the amount of curvilinear and rectilinear information present in each image using curved Gabor filters (Krüger, 2001): these curved Gabor filters are a product of a rotated complex harmonic wave function and a two-dimensional bent and rotated Gaussian function. It is formulated as follows:

$$B^{\overrightarrow{b}}(x,y)=r^{\overrightarrow{b}}\ast G^{\overrightarrow{b}}(x,y)\ast \left(F^{\overrightarrow{b}}(x,y)-D{C}^{\overrightarrow{b}}\right)$$

where $F^{\overrightarrow{b}}$ is the rotated complex harmonic wave function, $G^{\overrightarrow{b}}$ is the two-dimensional bent and rotated Gaussian function, and a vector $\overrightarrow{b}$ includes three variables: frequency, orientation and level of curvature. The bank of the curved Gabor filters is composed of 120 individual curved Gabor filters, including three spatial scales (frequency), eight orientations, and five levels of curvature. Each stimulus image was resized to 256 × 256 pixels and processed using local input divisive normalization (Pinto et al., 2008). The images were then convolved with the bank of curved Gabor filters, which produced 120 (3 × 8 × 5) curved Gabor coefficients, each presented as an image. Each curved Gabor coefficient image, including both the complex and real components, represented the result from a curved Gabor filter with a unique combination of a spatial scale, an orientation, and a level of curvature. The magnitudes of each curved Gabor coefficient image on each pixel were calculated as the square root of the sum of squared coefficients of complex and real components. Then, the largest magnitude across all 120 curved Gabor coefficient images was extracted for each pixel to create a peak curved Gabor coefficient image. This step eliminated responses produced by non-optimal curved Gabor filters, so that the peak curved Gabor coefficient image represented the optimal curved Gabor filter response to an image across scales, orientations, and levels of curvature.

The same procedure was repeated using the bank of rectilinear Gabor filters, composed of 3 spatial scales and 8 orientations, to generate 24 rectilinear Gabor coefficient images. Next, the largest magnitude across all 24 rectilinear Gabor coefficient images was extracted for each pixel to generate a peak rectilinear Gabor coefficient image. Then, the magnitude in the peak curved Gabor coefficient image was set to zero at a pixel if its magnitude was smaller than that in the peak rectilinear Gabor coefficient image in that pixel. The procedure went through all pixels to create a curved Gabor coefficient image with no rectilinear features represented, which we called a unique curved Gabor coefficient image. Finally, a curvilinear value of the stimulus image was produced by averaging the unique curved Gabor coefficient image across all pixels. The degree of curvature of our filters was essentially formalized by the result of a second polynomial function in two dimensions. In this framework, the sharpest tight curve would not break up to become a rectilinear corner and the shallowest curve would approach a straight line, but not become a straight line as long as the coefficient of the second-degree term was non-zero. Some of these steps are illustrated in Fig. S1.

Thus, at the end of this process, each image was assigned a curvilinear value. For each condition, a curvilinear value was produced by averaging all eight curvilinear values of the eight images in each condition. This curvilinear value represented the amount of curvature in that condition across scales, orientations, and levels of curvature. Similarly, the rectilinear values of each image were averaged to produce a rectilinear value for each condition, representing the residual intermediate feature information that was not captured by curvature information.

2.8. fMRI data analysis

2.8.1. Split-halves analysis

To transform functional data from all runs into the FreeSurfer surface space of a subject, we followed the same processing steps described in the Methods Section 2.6.1. For each subject, the surface-based functional data were spatially smoothed with a 2-mm Gaussian kernel for each run. Even runs of the surface-based functional data were concatenated and then regressed with the General Linear Model (GLM) such that each condition was modeled as a convolution of a boxcar with a human hemodynamic response function. We also included 3D motion correction measurements as nuisance variables to reduce the influence of head movement on the model fitting. A functional contrast between conditions was used to define the location and size of ROIs with statistical threshold at FDR < 0.05.

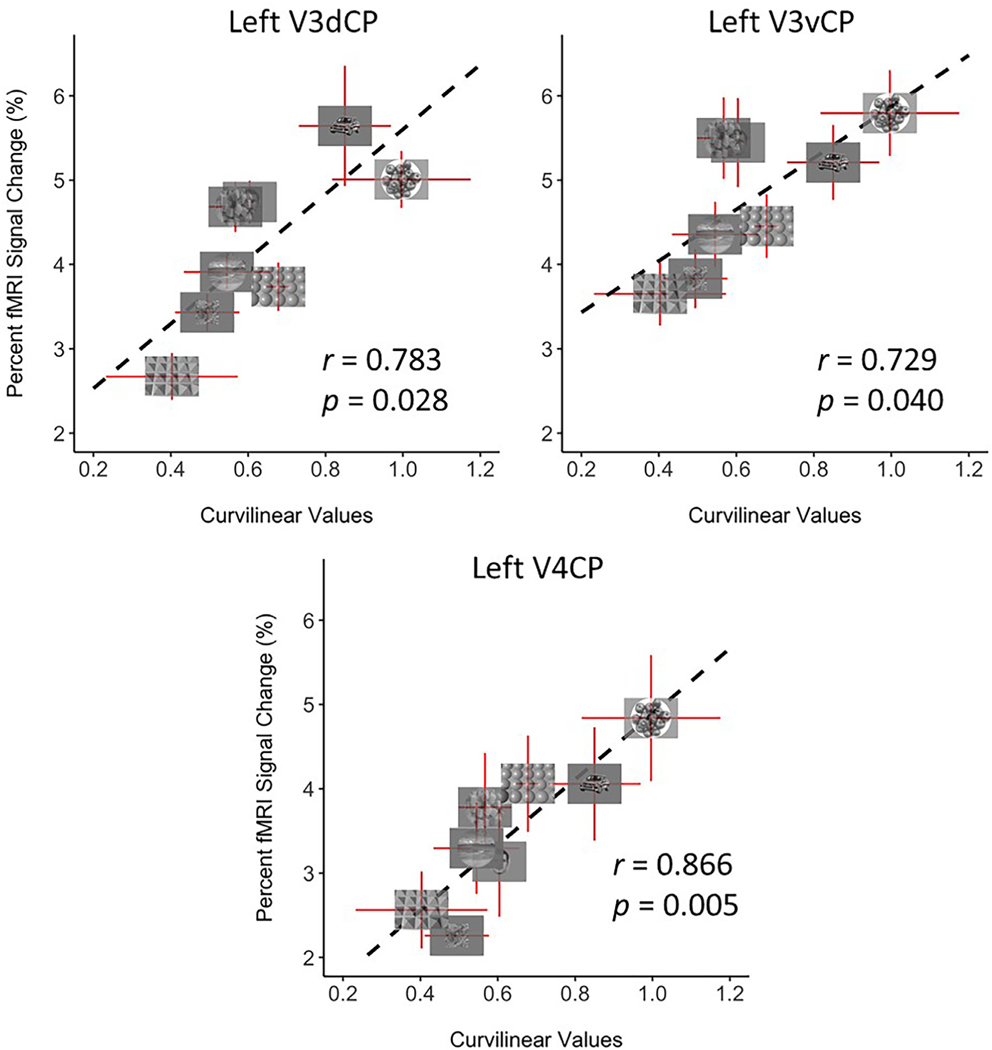
We then concatenated the odd runs of the surface-based functional data, which were fed into a GLM with the same number of regressors as those in the first part of the split-halves analysis to calculate the BOLD responses for each condition. Values from the ROIs defined from the even runs were extracted from this GLM fitting for ROI-based analysis to avoid double-dipping. To investigate the correlation between the curvilinearity of the images in each condition and the activity changes in these ROIs, curvilinear values were assigned to each condition by averaging the eight curvilinear values of all images in that condition. These curvilinear values were correlated with the beta estimates from the even runs for each ROI that were averaged across subjects to produce a single value of percent signal change for each condition (see Fig. 6).

Fig. 6.

Correlation of fMRI activity with curvilinear values in curvature-preferring patches was significant in left V3dCP (r = 0.763, p = 0.028), left V3vCP (r = 0.729, p = 0.040), and left V4CP (r = 0.866, p = 0.005), but not in right V3dCP/ V3vCP, V4CP (data not shown), or bilateral higher level curvature patches (OCP, FCP, see Fig. S2). All error bars represent the S.E.M. Significant correlations observed for left V3dCP, left V3vCP, and left V4CP suggest that these responses in curvature-preferring patches relate to simple curvilinear information. We did not observe significant correlations between the rectilinear values of the stimuli and fMRI responses in any of the curvature patches (Fig. S3).

2.8.2. Linear combination of simple curvature

We performed the following calculation to investigate whether complex curvilinear features derived from a linear combination of simple image curvature might account for fMRI response in curvature preference areas identified using fMRI.

Using the procedure described in Section 2.7, the 120 (3 spatial scales, 8 orientations, and 5 levels of curvature) curvilinear values generated for each image were collapsed across three scales and eight orientations, while keeping the curvature dimension (five levels of curvature in the curved Gabor filters) intact. This step yielded five curvilinear values, each representing one level of curvature regardless of scale and orientation. Given that performing a regression analysis with five regressors on eight values could be more sensitive to noise than using three regressors, we downsampled these five curvilinear values to three values to make the linear combination analysis more robust. In addition, this empirical decision facilitated comparison to our previous monkey study (Yue et al., 2014), which also used three curvilinear values. The grouping was performed as follows. The two pairs of curvilinear values describing the smallest and highest levels of curvature were averaged to yield two values representing a low and high level of curvature respectively; the curvilinear value with the middle level of curvature was kept intact. The three curvilinear values (low, medium, and high) generated for each image enabled us to determine whether a weighted combination of degrees of curvature could explain some of the brain activity.

The three curvilinear values from each image were averaged across images to generate low, medium, and high curvilinear values for each condition. The procedure was repeated for all eight conditions, resulting in twenty-four total curvilinear values.

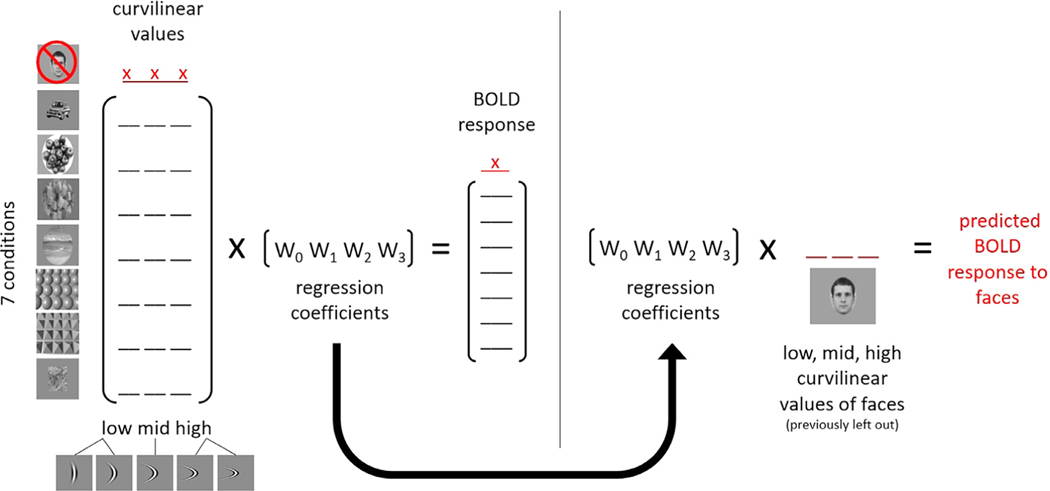
The fMRI responses to seven out of the eight conditions were regressed with their respective low, medium, and high curvilinear values, producing three regression coefficients and one intercept. The three curvilinear values from the condition excluded from the regression were then multiplied with the three regression coefficients and added together with the intercept to generate a predicted response for the condition left out from the regression. By repeating the steps using this leave-one-out method, we generated eight predicted responses (see Fig. 2).

Fig. 2.

Calculating predicted BOLD responses with a linear combination of simple curvilinear features. (Left) Low, middle, and high curvilinear values for each image were first generated by averaging the values of the two lowest and highest curvilinear degrees and leaving the middle value intact. Three curvilinear values (low, middle, and high) per condition (represented by underscores) were then calculated by averaging the three curvilinear values of the images in each condition. Seven conditions (e.g. excluding faces) were selected and each condition’s BOLD response was regressed with its respective curvilinear values. (Right) The matrix of regression coefficients from the seven conditions and the curvilinear values of the left-out condition (e.g. faces) were used to predict the BOLD response to that condition. This process was repeated to get a predicted BOLD response for each condition. x: indicates values left out of regression.

The above steps were applied to the activity data in each ROI for each participant individually. The mean predicted responses averaged across participants were correlated with the group averaged fMRI responses. To evaluate the statistical significance of the correlation, the same procedures were repeated for each participant, except that the 24 curvilinear values were randomly shuffled before generating the predicted response. The mean predicted responses from the permutation test were then correlated with the averaged fMRI response. This permutation test was repeated 5000 times to determine the p-value of the correlations, which are shown in Fig. 7.

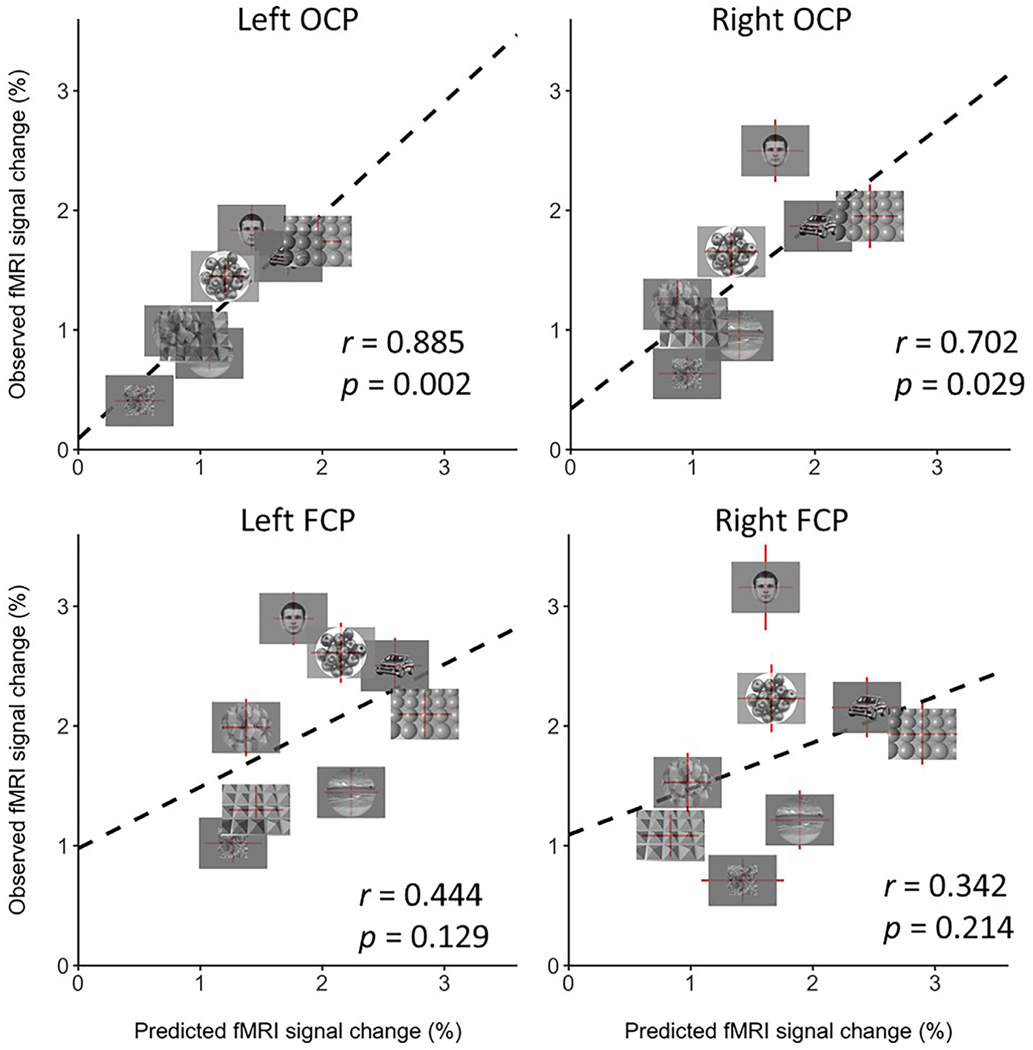
Fig. 7.

Correlation of the predicted fMRI response from the linear combination of curvature values with fMRI activity in OCP and FCP. The correlation is significant in left and in right OCP (left OCP, r = 0.885, p = 0.002; right OCP, r = 0.702; p = 0.029), but not in left and right FCP (left FCP, r = 0.444, p = 0.129; right FCP, r = 0.342, p = 0.214), suggesting that OCP plays a role in processing complex curvilinear information derived from simple curvilinear information (such as curved lines).

2.8.3. Principal component analysis (PCA)

The group PCA map was generated using the following procedure. For each subject, the percent signal change of each surface vertex in FreeSurfer averaged surface space (see section on group-level random-effects analysis) was normalized by dividing the percent signal change value with the standard deviation of that surface vertex. Then, the normalized data were averaged across subjects to create a single value for each surface voxel for each condition, which generated an 8 × N matrix where 8 represents the number of conditions and N represents the number of surface vertices. We selected surface vertices with significantly larger group-level responses to visual stimuli (all 8 conditions) than to fixation on a blank screen (FDR < 0.05) to feed into the PCA analysis. Thus, to avoid confounds with our ROI-based curvature preference analysis, PCA was performed on all visually responsive surface vertices.

These group data were fed into MATLAB to perform PCA, in which each condition represents a variable and each surface vertex represents an observation. The PCA produced eight principal components and its associated loadings (eigenvectors). Then, we correlated the loading of each principal component with the curvilinear and rectilinear values calculated using the above procedure to determine whether there were principal components related to either curvilinear or rectilinear features. Finally, the PCA component that was significantly correlated with the curvilinear values was projected back on to the brain to illustrate the PCA pattern.

PCA maps for individual subjects were created with the same procedure used for the group PCA map. Instead of group-averaged data, individual subjects’ visually responsive surface vertices were fed into the PCA analysis.

To explore the possibility that the outcome of the PCA analysis arose from a sizable contribution of activity elicited by face stimuli, we repeated the PCA analysis using the same procedure described above at group and individual level without the data generated by face stimuli.

3. Results

3.1. Map of cortical regions with curvature response preference

By contrasting the fMRI responses to round objects and arrays of spheres with the responses to rectilinear objects and arrays of four-sided pyramids, we observed significantly greater activation to the curvilinear than rectilinear shapes in multiple brain areas at both the group-(random effects analysis, see Methods Section 2.6.2) and individual-subject levels (Methods Section 2.6.3).

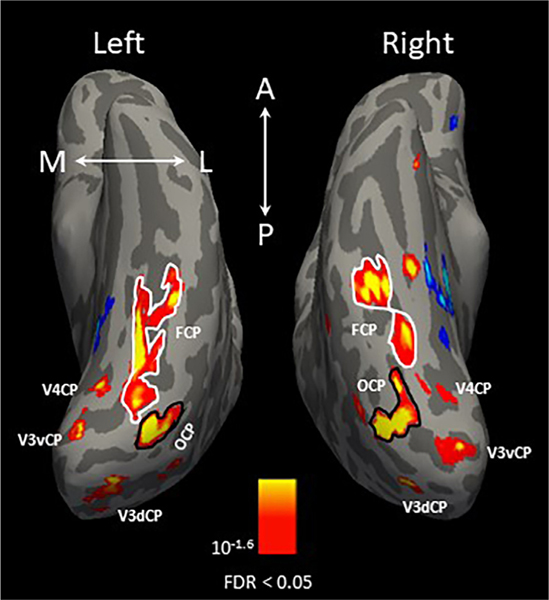
Fig. 3 shows a map of cortical regions with curvature preference from a single example subject, with significantly higher responses to curvilinear shapes shown in yellow/red. Multiple curvature-preferring patches were identified in this subject, three of which were located in retinotopically identified early visual areas: dorsal and ventral V3, and V4 in both hemispheres, which we termed as V3dCP, V3vCP, and V4CP. Two more patches with curvilinear response preferences were found in the lateral occipitotemporal cortex (occipital curvature preference patch, OCP, encircled in a solid black line) and fusiform gyrus (fusiform curvature preference patch, FCP, encircled in a solid white line).

Fig. 3.

A cortical map of regions with strong curvature response preference in a single example subject. The map was produced by contrasting the fMRI responses to curvilinear (round shapes and computer-generated 3D sphere array) > rectilinear (rectilinear shapes and computer-generated 3D pyramid array) stimuli. The yellow/red activation indicates the curvature response preference; blue/cyan activation indicates the rectilinear response preference. Three of the five curvature-preferring patches were located in dorsal and ventral V3, and V4 in both hemispheres, which we termed as V3dCP, V3vCP, and V4CP. Black outlines indicate boundaries of the occipital curvature patch (OCP), located in the lateral occipitotemporal cortex, and white outlines indicate boundaries of the fusiform curvature patch (FCP), located in the fusiform gyrus. The orientation of the brains are indicated in white letters (A = anterior; P = posterior; M = medial; L = lateral).

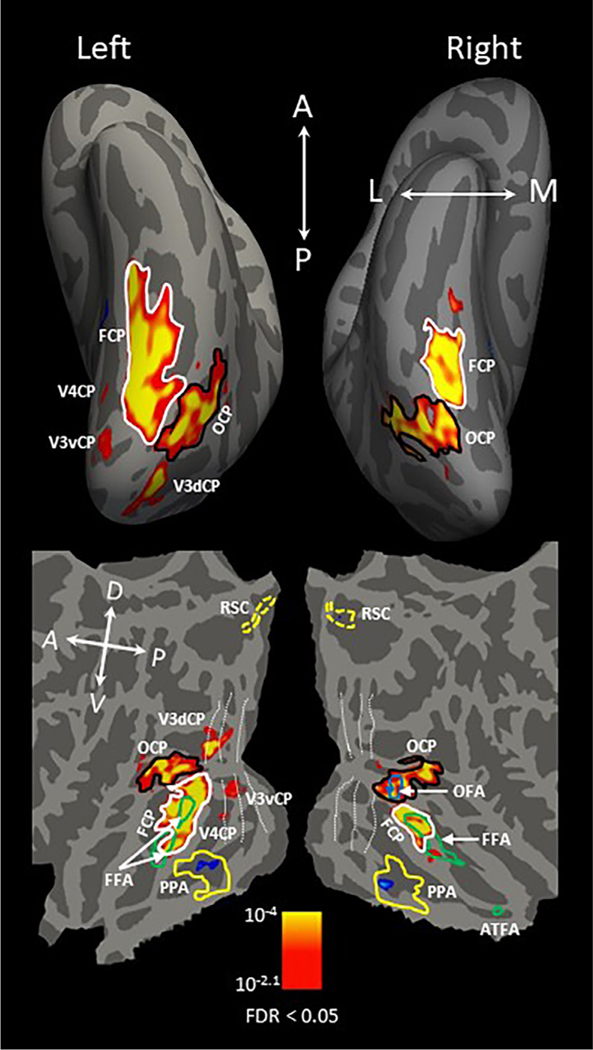
At the group level, shown in Fig. 4, the curvature-preferring patches (V3dCP, V3vCP, and V4CP) located in the early visual cortex were observed in only the left hemisphere, with a corrected statistical threshold of FDR < 0.05. In addition, OCP was located within the inferior occipital gyrus, extending anteriorly to MT in both hemispheres; FCP was located bilaterally within the fusiform gyrus lateral to the middle Fusiform sulcus (Nasr et al., 2011) or mid-Fusiform sulcus (Weiner et al., 2014).

Fig. 4.

Group-averaged cortical map of curvature-preferring regions projected onto the freesurfer averaged inflated brain (top) and a flattened brain (bottom). The map was generated by contrasting fMRI responses to curvilinear (round shapes and computer-generated 3D sphere array) > rectilinear (rectilinear shapes and computer-generated 3D pyramid array) stimuli, the same contrast as in Fig. 3. Red/yellow activation indicates curvature response preference, and blue/cyan activation indicates rectilinear response preference. The dotted white lines shown on the flattened brain (bottom) indicate the retinotopic boundaries between early visual areas identified by the retinotopic mapping runs. Black lines indicate the boundary of OCP and solid white lines indicate the boundary of FCP. The blue outline shows the boundary of the occipital face area (OFA) and green lines show the boundaries of the fusiform face area (FFA) and anterior temporal face area (ATFA). The right OCP completely overlapped the right OFA and bilateral FCP partially overlapped FFA in both hemispheres (see Section 3.3 for quantification). Scene-selective areas were defined by fMRI responses to scenes > curvilinear and rectilinear stimuli. Yellow lines indicate the boundary of the parahippocampal place area (PPA) and dotted yellow lines outline retrosplenial cortex. The rectilinear-preferring patch overlapped PPA bilaterally (see Section 3.3 for quantification). The corrected statistical threshold was FDR < 0.05. Local orientations of the brain axes on the flattened brain are indicated in white letters (D = dorsal; V = ventral; P = posterior; A = anterior).

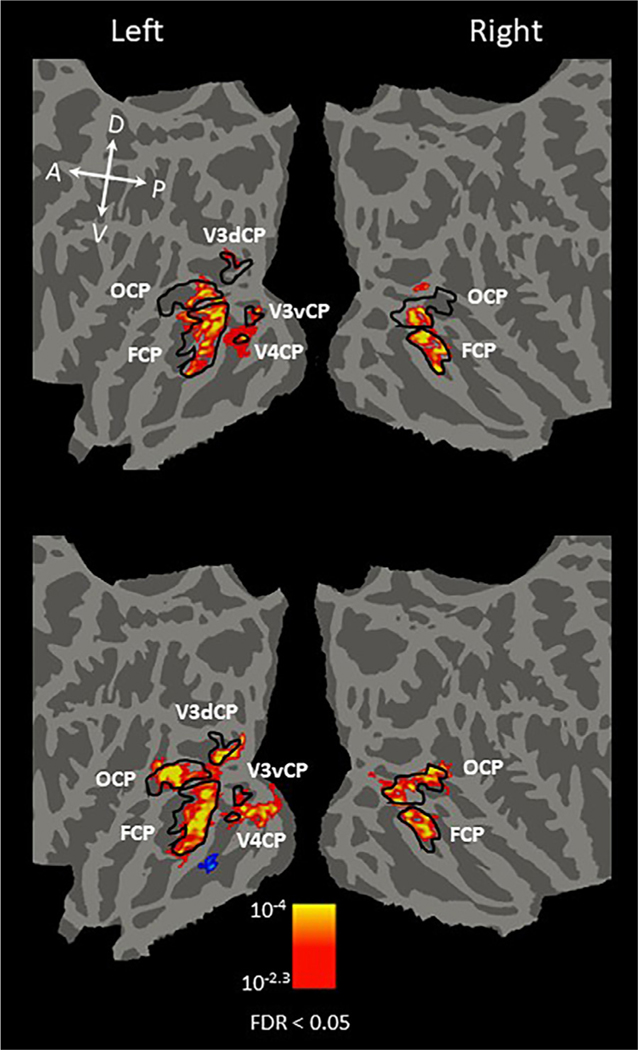
The differences in visual extent between the round and rectilinear object stimuli and the computer-generated sphere and pyramid stimuli were expected to affect responses, particularly in early visual cortex. To assess the consistency of curvature response preference across stimulus type, we also created two separately defined curvature preference maps: one contrasting fMRI responses to round objects with the responses to rectilinear objects (Fig. 5, top), and the other contrasting fMRI responses to array of spheres with the responses to array of pyramids (Fig. 5, bottom). As the image size of the computer-generated stimuli (20 × 15˚) covering the whole screen is larger than those of the real-world objects (15˚ in radius), we observed more early visual areas activated by the computer-generated stimuli than real-world objects in the left hemisphere. However, all curvature-preferring regions observed in the combined map (Fig. 4) are present in the separated maps, suggesting the consistency of the curvature response preference across stimulus type.

Fig. 5.

Comparison of group-averaged cortical maps of regions with significant curvature response preference across stimulus type (conditions 1 and 2 vs. conditions 3 and 4). Group-averaged maps were projected onto the FreeSurfer averaged flattened brain. The map on the top was generated using the fMRI activity contrast of round > rectilinear real-world objects. The map on the bottom was generated using the fMRI activity contrast of computer-generated 3D sphere array > computer-generated 3D pyramid array. Yellow/red activation indicates the curvature response preference; blue/cyan indicates the rectilinear response preference. Black outlines indicate the boundaries of the curvature-preferring patches. As expected, because the image size of the computer-generated stimuli was larger than that of the real-world objects, we observed more early visual areas activated by the computer-generated stimuli (top) than real-world objects (bottom). However, all curvature-preferring regions observed in the combined map (Fig. 4) are present in the separated maps, indicating the consistency of curvature preference regions across stimulus type. The corrected statistical threshold was FDR < 0.05. Local orientations of the brain axes on the flattened brain are indicated in white letters (D = dorsal; V = ventral; P = posterior; A = anterior).

3.2. The topographic relationship between face-selective and curvature-preferring areas

Our monkey fMRI study (Yue et al., 2014) demonstrated a significant overlap between the curvature-preferring and face-selective areas in the visual cortex. It was thus of great interest to examine whether the close proximity between these two networks also exists in humans. In the same experiment, face-selective areas were localized in the human ventral visual cortex by contrasting fMRI activation evoked by faces (condition 5) with that evoked by objects (condition 7). As shown in the group-level analysis (Fig. 4), we found two face-selective areas (solid green outline) in the left hemisphere located in the fusiform gyrus, identified in prior studies as the fusiform face area 1 (FFA1) and fusiform face area 2 (FFA2), respectively (Pinsk et al., 2009; Weiner et al., 2010; Julian et al., 2012). In the right hemisphere, we found three face-selective areas (Fig. 4): the occipital face area (OFA, Gauthier et al., 2000; solid blue outline), a single fusiform face area (FFA, Kanwisher et al, 1997; solid green outline), and a face-selective patch in the anterior inferior temporal cortex (aIT, Zhang et al., 2016; solid green outline).

To quantify the percentage of overlap between these curvature-preferring patches and face-selective areas, we calculated the number of vertices shared between two ROIs divided by the total number of vertices of the ROI (± standard error of mean). As shown in Fig. 4, in the both hemispheres, FCP partially overlapped FFA. On average, the overlapped region between FCP and FFA accounted for 42.45% (± 2.30) of total FCP and 58.96% (± 4.86) of total FFA in the left hemisphere, and, in the right, 63.73% (± 4.06) of total FCP and 39.96% (± 3.34) of total FFA. OFA, which was only identified in the right hemisphere at the group level, completely overlapped OCP. On average, the overlapped region between OCP and OFA accounted for 47.32% (± 2.45) of total OCP, and 100% of OFA.

3.3. Relationship between quantitative measures of image curvature and responses in curvature preferring patches

To investigate the functional properties of cortical patches with significant preference for curvature, we defined regions of interest (ROIs) in each subject as all curvature-preferring patches identified using the functional contrast of (round objects plus arrays of spheres) > (rectilinear objects plus arrays of pyramids). The ROIs were defined using half of the functional data (see Section 2.8.1) with a statistical threshold of FDR < 0.05. With this method, left V3dCP /V3vCP was identified in fourteen subjects, left V4CP in twelve subjects, left OCP and FCP in all fifteen subjects, right V3dCP/V3vCP in six subjects, right V4CP in eight subjects, and right OCP and FCP in all fifteen subjects. We then extracted values of ROIs from the held-out data to perform ROI-based correlation analysis (see Section 2.8.1).

We correlated the fMRI response in curvature-preferring patches with curvilinear values of visual stimuli to investigate which curvature-preferring patches were involved in processing simple curvilinear information, such as curved lines that could be modeled and quantified by curved-Gabor filters. We found significant correlations in left V3dCP (r = 0.763, p = 0.028), left V3vCP (r = 0.729, p = 0.040), left V4CP (r = 0.866, p = 0.005), shown in Fig. 6. By contrast, fMRI activity did not correlate significantly with curvilinear values in the other curvature-preferring ROIs in higher level visual cortex (Fig. S2: left OCP, r = 0.579, p = 0.132; left FCP, r = 0.643, p = 0.086; right OCP, r = 0.495, p = 0.212; right FCP, r = 0.554, p = 0.155). These results suggest that the curvature-preferring patches located in the early visual areas, such as left V3dCP/V3vCP and left V4CP, are involved in processing simple curvilinear information, such as curved lines, that could be modeled and quantified by curved-Gabor filters (see Methods Sections 2.7 and 2.8.1).

We performed an additional analysis to determine the extent to which the activity in higher-level curvature-preferring regions could be related to information from a linear combination of curvature values (see Methods Section 2.8.2 and Fig. 2). The low, medium and high curvature weights generated from this analysis are included in Supplementary Tables 1 and 2. Our results, shown in Fig. 7, demonstrate that the weighted linear combination of simple curvilinear features significantly accounted for the fMRI response in bilateral OCP (left OCA, r = 0.885, p = 0.002; right OCP, r = 0.702; p = 0.029), but not in FCP (left FCP, r = 0.444, p = 0.129; right FCP, r = 0.342, p = 0.214). Taken together, these results suggest that the information processing in OCP is related to complex curvilinear information derived from simple curvilinear information (such as curved lines). By contrast, FCP is likely involved in more complex curvilinear information processing that cannot be derived from the linear combination of simple curvilinear information.

As shown in Fig. 7, face stimuli with modest curvilinear values produced the largest response in higher level curvature-preferring areas. This suggests that the computational model deployed here to quantify curvilinear information present in our stimuli could not ideally or efficiently model the information in face stimuli with simple curved Gabors and their linear combination. For example, it has been suggested that faces are processed holistically, a computation that cannot be modeled by our quantitative model. Thus, our curvature model could lack the power to capture complex curvilinear information that may be characteristic of face stimuli.

Note that we do not assert that the activity in FFA, a region that systematically overlaps with the FCP, can be explained entirely by our quantitative curvature model, or by curviness of faces as compared to other non-curvy objects alone. Curvature response preference was defined by contrasting fMRI response to stimulus conditions with naturally occurring differences in curvilinear and rectilinear appearance. Thus, on this definition, regions of FFA that overlap with FCP would be considered curvature-preferring. The computational model was used to quantify the stimulus information related to the activity of curvature-preferring regions in terms of simple curvature, i.e., curved Gabors and their linear combination. Indeed, the lack of a significant correlation between FCP activity predicted by a linear combination of curved Gabors and the observed FCP activity suggests that nonlinear combinations of curvilinear information might explain the observed activity in FCP. For example, the finding that face stimuli produced the highest fMRI response in left and right FCP could be caused by the holistic, nonlinear processing of faces that our model cannot predict.

3.4. Regions with rectilinear response preference

As shown in Fig. 4, we found bilateral rectilinear-preferring areas (highlighted in blue/cyan) located within the parahippocampal place area (Epstein and Kanwisher, 1998; PPA, encircled in solid yellow line) in all subjects using a corrected threshold of FDR < 0.05. We did not find significant correlation of the rectilinear values of visual stimuli with the fMRI activation in the rectilinear patches (Fig. S4: for left, r = 0.071, p = 0.867; or for right, r = 0.197, p = 0.640). This suggests the rectilinear patches might be involved in processing complex rectilinear information that could not be captured by our model.

3.5. PCA map

Applying PCA to our data allowed us to explore a large-scale topographic pattern related to curvilinear information of visual stimuli in visual cortex beyond what a simple contrast of fMRI response between conditions can provide (e.g., Connolly et al., 2016). PCA analysis takes a holistic view of data by taking into account activity variance among voxels across the whole brain. The result of the PCA thus clusters voxels that have similar response profiles across conditions together, thereby revealing a spatial pattern among voxels across the whole brain. Such a pattern is difficult to identify by using simple contrasts between conditions because simple contrasts do not take into account the activity relationship between voxels, as it treats each voxel independently.

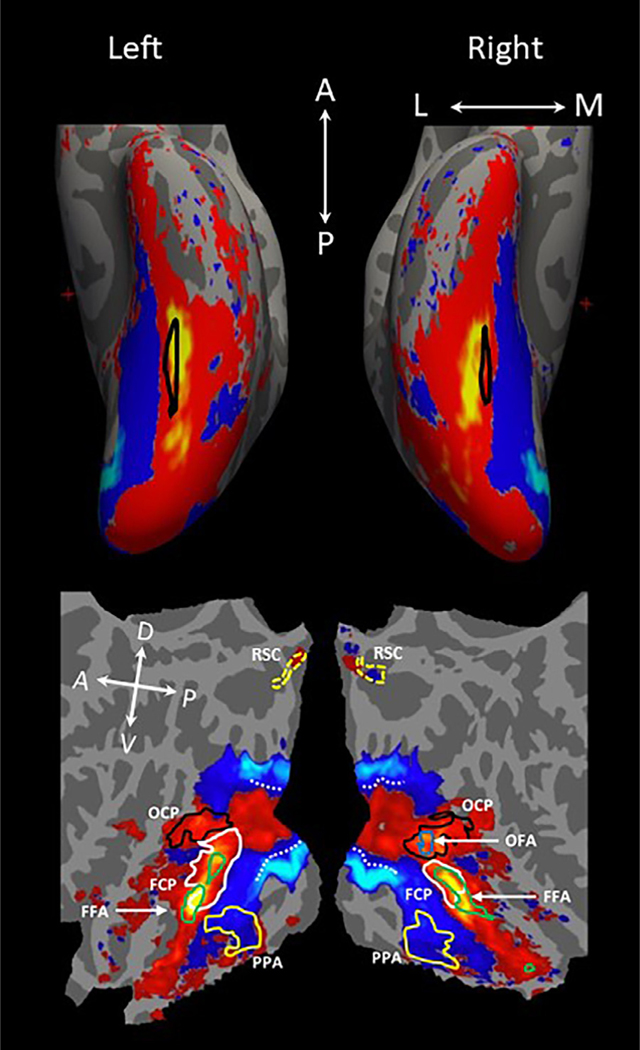
As the loading of the second principal component (PC2) correlated significantly with the curvilinear values of visual stimuli across conditions (Fig. S5: r = 0.85, p = 0.007 for left hemisphere; r = 0.79, p = 0.019 for right hemisphere, permutation test: see Section 2.8.3), and not with the rectilinear values (Fig. S8, left: r = 0.286, p = 0.493; Fig. S9, right: r = 0.312, p = 0.452), PC2 was determined to be relevant to the curvilinearity of visual stimuli. PC2 accounted for 9.96% of the total variance in neural response. Correlations between the remaining PCs and curvilinear and rectilinear values are included in the supplementary materials (Figs. S6–9), as is the percentage of variance explained by each PC (Fig. S10). To understand the spatial pattern of the PC2, we projected the PC2 generated with the group data onto the averaged brain (Fig. 8). The areas in red/yellow had positive PC2 values; the areas in blue/cyan had negative PC2 values. The PC2 maps generated using the individual data was consistent across subjects (see Fig. 9), mirroring the group PC2 map.

Fig. 8.

Group PCA map. (top) Inflated view of the ventral surface. Areas outlined in black on the inflated brain indicate the location of the mid-fusiform sulcus. Visual areas in red/yellow were associated with positive values of the second principal component (PC2) while those in blue/cyan were associated with negative PC2 values. (bottom) Flattened view of the ventral surface. The visual cortex associated with the positive PC2 values included OCP (black outline), FCP (white outline), OFA (blue outline), FFA (green outline); the visual cortex associated with the negative PC2 values encompassed PPA (yellow outline) and rectilinear-preferring areas (not outlined, see Fig. 4). The absolute values of PC2 are not meaningful, because the data were normalized in the PCA analysis. Given that the loading of PC2 correlated significantly with the curvilinear values of visual stimuli across conditions (Fig. S5: r = 0.85, p = 0.007; permutation test: see Methods), the areas in red/yellow might be involved in processing curvilinear features and those in blue/cyan might be implicated in processing rectilinear features. The dashed white line indicates the central-peripheral boundary in our stimuli defined by contrasting the fMRI response to computer-generated 3D spheres and pyramid arrays (20 × 15˚) vs. faces and objects (8.4 × 10.0˚). Local orientations of the brain axes on the flattened brain are indicated in white letters (D = dorsal; V = ventral; P = posterior; A = anterior).

Fig. 9.

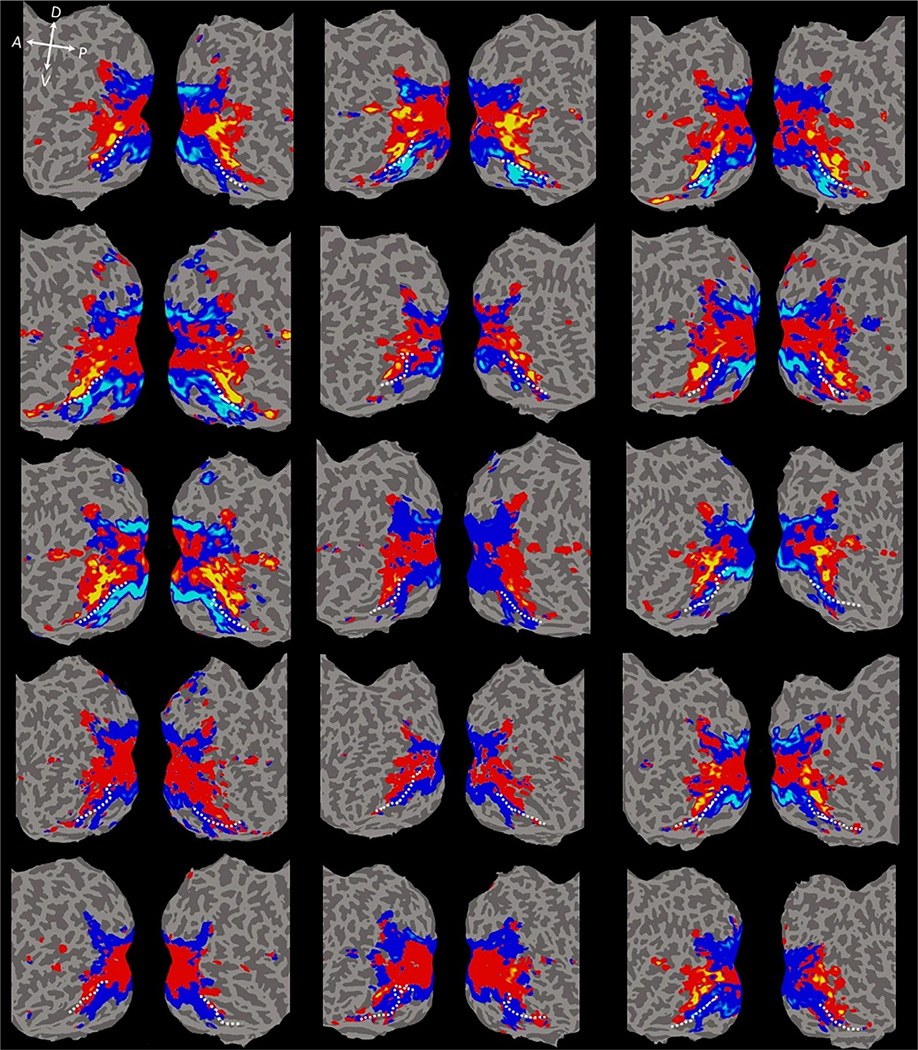
Individual subject PCA maps. Each subject’s data (N = 15) were projected onto their native flattened surface. Relatively consistent across all subjects, the visual cortex associated with positive PC2 values was confined within the central visual field in the early visual areas, and then extended continuously to the anterior temporal lobe through lateral occipitotemporal areas. Regions of visual cortex associated with negative PC2 values extended from peripheral visual field representations in early visual areas to the medial surface of the occipitotemporal cortex and then to the collateral sulcus (CoS) and parahippocampal gyrus. The dashed white line indicates the anatomical border between the fusiform gyrus and the collateral sulcus. Local orientation of the brain axes on the flattened brain are indicated in white letter (D = dorsal; V = ventral; P = posterior; A = anterior).

As shown in Fig. 8, the visual cortex associated with positive PC2 values was confined within the central visual field representations in the early visual areas, and then extended continuously to the anterior temporal lobe through lateral occipitotemporal areas. The visual cortex associated with negative PC2 values extended from peripheral visual field representations of early visual areas to the medial surface of the occipitotemporal cortex to the collateral sulcus (CoS) and parahippocampal gyrus. The transition boundary from positive to negative PC2 was located between the fusiform gyrus and CoS. The visual cortex associated with the positive PC2 values encompassed OCP (blue outline), FCP (white outline), OFA (blue outline), FFA (green outline); the visual cortex associated with the negative PC2 values encompassed PPA (yellow outline) and rectilinear-selective areas. This map suggests that the areas associated with positive PC2 values might be involved in processing curvilinear features while those associated with negative PC2 values might be implicated in processing rectilinear features. Similar PC2 maps were observed in all 15 individual subjects (Fig. 9).

The group (Fig. S11) and individual (Fig. S12) PCA maps generated without data from the face condition are similar to those generated with the data from all conditions (Figs. 8 and 9), which suggests that PCA maps generated from this experiment are not primarily driven by responses to the face condition.

4. Discussion

4.1. Comparison of curvature-processing networks in humans and monkeys

In a previous fMRI study, we identified three curvature-preferring patches in the monkey ventral visual pathway: (1) a posterior curvature patch (PCP) in dorsal V4; (2) a middle curvature patch (MCP), anterior to PCP, in the posterior superior temporal sulcus (STS) within the posterior inferior temporal cortex (cytoarchitectonic area TEO); and (3) an anterior curvature-preferring patch (ACP) within the anterior inferior temporal cortex (anterior area TE) just ventral to the STS (Yue et al., 2014). Consistent with our monkey results, we observed multiple curvature-preferring patches in human visual cortex, located in retinotopic areas (V3vCP, V3dCP, V4CP), as well as in occipital (OCP) and temporal (FCP) cortex.

The computational models employed here to quantify the curvilinearity of visual stimuli were not intended to represent the underlying computation occurring in the curvature-preferring areas we identified. Instead, our two metrics of the relationship between curvilinear information and neural responses—(1) the significant correlations between fMRI responses and simple curvilinear information in early curvature patches and (2) significant prediction of fMRI response in OCP based on more complex linearly combined curvature information—and our inability to capture the relationship using these two metrics in the curvature patch farthest along in the visual hierarchy (FCP) suggest to us an increase in processing complexity of curvilinear information along the visual pathway.

First, fMRI responses in retinotopically defined curvature-preferring patches in both monkeys and humans correlated significantly with the amount of curvilinear information in the visual images, suggesting that they are involved in processing simple curvilinear information in an image (e.g. curved lines). These results are consistent with electrophysiological recordings in monkeys showing that some dorsal V4 neurons are strongly selective for curved contours (Pasupathy and Connor, 1999) and patterns (Gallant et al., 1996), and fMRI studies demonstrating that human V4 is activated preferentially by curved shapes relative to radial gratings (Wilkinson et al., 2000).

Second, fMRI responses in both monkey MCP and human OCP showed significant correlation with the predicted response derived from a linear combination of simple curvilinear features, suggesting that they may play a critical role in processing complex curvilinear information composed of an integration of simple curvilinear information. Consistent with the functional properties of monkey MCP and human OCP, electrophysiological recordings (e.g., Brincat and Connor, 2004) have demonstrated that some TEO neurons’ responses to complex shapes can be modeled by the linear addition of their responses to the parts of the complex shapes.

Third, monkey and human curvature-preferring patches in temporal cortex (ACP in monkeys and FCP in humans) are likely involved in more complex curvilinear information processing that cannot be derived from the linear combination of simple curvilinear features. This functional similarity of the curvature-processing network in monkeys and humans suggests that curvature is a fundamental visual feature whose processing is conserved across primate species.

The precise computation in these curvature patches could not be determined using the current dataset. Future experiments using electrophysiological recording might be necessary to elucidate the exact computations occurring in these curvature patches.

4.2. Operationalizing curvature: comparisons with other studies

Curvature is a complex intermediate level visual feature that can be defined in a number of ways. The computational model employed here to quantify the amount of curvature in our stimuli allowed us to extract curvilinear information at multiple spatial scales, orientations, and degrees and investigate how outputs from two methods of summarizing that information for a given image (peak curved Gabor value and linear combination) relate to neural responses. It is worth noting that the curvilinearity measure generated by our model was recently shown to significantly correlate with perceived curvilinearity of complex visual stimuli (Zachariou et al., 2018). This suggests that our model captures some aspects of stimulus information related to curvature perception in humans.

A canonical V4 electrophysiology study (Pasupathy and Connor, 1999) used stimuli created by smoothing out sharp-angled simple shapes, which were generated to target the selectivities of V4 neurons specifically. Compared to our curvature conditions—round, natural objects and computer-generated spheres—the curved stimuli used were not entire smoothly curved like ours and only included simple shapes, precluding investigation of curvature processing across visual cortex for more naturalistic objects.

Multiple recent fMRI studies have investigated curvature response preferences in monkeys and humans (e.g., Srihasam et al., 2014; Long et al., 2018). Srihasam et al. (2014) presented curvy and rectangular patterns to monkeys to define curvature response preference in the visual cortex. The curvature stimuli in their study were rectangle shapes with wavy curvy lines. As the global shapes of their curvature stimuli were rectilinear, they might have activated rectilinear-preferring areas instead of curvature-preferring areas in later stages of the visual processing pathway where the receptive field of neurons could be large enough to cover the whole stimulus instead of local areas. Consequently, their stimuli were not ideal for mapping out all curvature-preferring regions across the entire ventral visual pathway. By contrast, our curvature stimulus set included local curvature as well as global curvature (with the exception of the overall rectangular aperture of the computer-generated sphere and pyramid arrays due to their whole screen presentation), which makes it more likely to uncover all curvature-preferring regions in the entire visual cortex.

The recent study by Long et al. (2018) beautifully demonstrated that mid-level features (such as curvilinearity) underlie the topographic representation of perceptual categorization, such as animacy. Their stimuli, which they called texforms, were unrecognizable object/animal images rendered by distorting the global shape of the original images while maintaining the mid-level features of the original images. Long et al.’s treatment of curvature in their stimuli differ from ours in three ways. First, their primary metric of curvilinearity was perceptual ratings of ‘curviness’ and ‘boxiness’. Although our computational measure has been shown to correlate with perceptual ratings (Zachariou et al., 2018), our quantification of curvature allows us to systematically separate the contributions of curvilinear and rectilinear information in our images. Second, the global shape distortion in Long and colleagues’ stimuli preclude the input of global features that could convey curvature information, while our stimuli contain both local and global curvature information. Third, although participants were unable to identify the original objects at a basic category level in the texform stimuli, the stimulus conditions separated animate and inanimate objects, which subjects on average rated as appearing more ‘curvy’ or ‘boxy’, respectively (see Zachariou et al., 2018). Our stimulus set was designed to avoid explicit categorical distinctions between stimulus conditions. Therefore, differences in the fMRI responses to our visual stimuli were more likely to be driven primarily by differences in the curvilinearity of the visual stimuli.

4.3. PCA maps

PCA analysis revealed visual areas associated with positive PC2 values, indicative of curvature preference, located within the central visual field representations of early visual areas and extending forward through lateral occipitotemporal regions to the anterior temporal lobe. Interestingly, visual areas associated with positive PC2 values encompassed curvature-preferring patches and face-selective areas, implying that those functionally specialized areas might be related to curvilinear features of visual stimuli. Consistent with the observations in our PC2 map of the adult human brain (Fig. 8), recent monkey fMRI studies (Srihasam et al., 2014; Arcaro and Livingstone, 2017) have shown that curvature-biased areas extend from the central visual field in early visual areas to the anterior temporal cortex in both adult and infant monkeys.

Anatomically, visual areas associated with positive PC2 values encompassed animate-processing visual areas located on the lateral surface of ventral temporal cortex while those associated with negative PC2 values encompassed inanimate-processing visual areas located the medial surface of ventral temporal cortex (e.g., Grill-Spector and Weiner, 2014), indicating that animate-inanimate categorization might rely in part on curvilinear features. Recent behavioral (Long et al., 2017; Zachariou et al., 2018) and fMRI (Long et al., 2018) studies support this conclusion. Arcaro and Livingstone (2017) observed a curvature response preference map that encompassed face-selective cortical areas in an infant monkey (186 days old), at least as early as face-selective areas emerge in the infant monkey’s IT cortex. The potential for antecedent development of curvature preferring areas relative to face-selective areas suggests a plausible mechanism by which curvilinearity contributes to the establishment of category selectivity in IT cortex.

4.4. Rectilinear-preferring patches in humans

Our previous monkey fMRI study identified two rectilinear-preferring patches, one of which was located near the posterior middle temporal sulcus—close to scene-selective patches in monkeys (e.g. Nasr et al., 2011), which are considered homologous to PPA, a scene-selective area in humans. In the current human experiment, we localized the rectilinear-preferring patches in the PPA. Previous work has shown that the PPA produces a greater fMRI response to rectilinear shapes compared to curved shapes (Nasr et al., 2014) and natural scenes with high spatial frequency content compared to scenes with low spatial frequency content (Rajimehr et al., 2011). This evidence suggests that rectilinear stimuli and objects with high pass filtering might be preferentially processed in scene-processing areas, supporting our finding of rectilinear-selective patches in PPA. Our findings are also compatible with previous reports that PPA has a peripheral visual field bias (Levy et al., 2001; Hasson et al., 2003; Schwarzlose et al., 2008).

4.5. Organization of visual cortex

Ungerleider and Mishkin (1982) showed that lateral striate lesions in monkeys, affecting central vision, played a particularly important role in temporal lobe function (pattern discrimination task), whereas lateral and medial striate lesions, affecting central and peripheral vision respectively, equally affected temporal lobe and parietal lobe function (landmark task). The current study highlights the importance of the visual field in the processing of different kinds of visual information (Figs. 4, 8 and 9). Consistent with Mishkin and Ungerleider’s (1982) results, Livingstone and colleagues demonstrated with monkey fMRI that faces and curvilinear shapes are represented predominantly in the central visual field representation in IT cortex, and objects and rectilinear shapes are represented primarily in the peripheral visual field representation in both adult (Srihasam et al., 2014) and infant monkeys (Livingstone et al., 2017; Arcaro and Livingstone, 2017). Interestingly, the central-peripheral map of shape representation correlated with a curvature-rectilinear map in IT cortex in both adult and infant monkeys. Together it has been argued that retinotopy, in conjunction with curvilinearity, is a primary organizing principle for the temporal cortex, which was termed retinotopic proto-organization (Srihasam et al., 2014; Arcaro and Livingstone, 2017). Our current results in humans (Figs. 8 and 9) are consistent with this argument, revealing the similarity of temporal cortex organization between human and nonhuman primates.

Behavioral studies have shown that visual acuity for curvature discrimination decreases as eccentricity increases (e.g. Whitaker et al., 1993). Consistent with these behavioral findings, a recent electrophysiological study found that the curvature tuning preference of neurons in V1 and V4 decreased as a function of eccentricity (Ponce et al., 2017). Therefore, we hypothesize that, early in development, curvilinear objects are more frequently foveated to exploit the enhanced magnification of the central visual field, where small local changes characteristic of predominantly curvilinear visual stimuli can be more readily distinguished, while rectilinear object processing may be accomplished by peripheral vision. Such a difference in viewing requirements might bias the developing visual system to process curvilinear objects in regions of the visual cortex that represent the central visual field, driving rectilinear objects to be processed in peripheral visual field representations (e.g. Figs. 4, 8 and 9). Further studies are necessary to investigate this hypothesis.

A recent study demonstrated that extensive viewing of Pokémon characters at consistent size and location in the visual field during development can result in a consistent functional topography of that stimulus representation in adulthood (Gomez et al., 2019). For experienced subjects (Fig. 3), Pokémon maps spatially overlapped and extended laterally from regions preferentially responding to stimuli with the curviest appearance (faces) and never extended medially to regions preferentially responding to stimuli with the most rectilinear appearance (corridors). Pokémon-selective voxels underlying this map also exhibited a foveal bias. Similarly, our study demonstrates that curvature may interact with eccentricity biases to drive the consistent topography of curvature-preferring regions.

4.6. Conclusion

Our results demonstrate a specialized cortical network for curvature processing in humans and lend support to the view that curvilinearity preference interacts with central-peripheral processing biases as an important organizing principle for temporal cortex topography in the adult human brain.