An ensemble approach for multi-stage transfer learning models for COVID-19 detection from chest CT scans

Abstract

The novel coronavirus outbreak of 2019 reached pandemic status in March 2020. Since then, many countries have joined efforts to fight the COVID-19 pandemic. A central task for governments is the rapid and effective identification of COVID-19 positive patients. While many molecular tests currently exist, not all hospitals have immediate access to these. However, CT scans, which are readily available at most hospitals, offer an additional method to diagnose COVID-19. As a result, hospitals lacking molecular tests can benefit from it as a way of mitigating said shortage. Furthermore, radiologists have come to achieve accuracy levels over 80% on identifying COVID-19 cases by CT scan image analysis. This paper adds to the existing literature a model based on ensemble methods and 2-stage transfer learning to detect COVID-19 cases based on CT scan images, relying on a simple architecture, yet complex enough model definition, to attain a competitive performance. The proposed model achieved an accuracy of 86.70%, an F1 score of 85.86% and an AUC of 90.82%, proving capable of assisting radiologists with COVID-19 diagnosis. Code developed for this research can be found in the following repository: https://github.com/josehernandezsc/COVID19Net.

1. Introduction

2019 witnessed the outbreak of a new virus, named COVID-19, caused by a coronavirus strain identified as SARS-CoV-2. In March 2020, the situation evolved to a global health crisis, as the WHO announced the COVID-19 outbreak to be a pandemic. Timely identification of COVID-19 patients became a priority to fight this pandemic and several methods, such as molecular tests, are at the front line to detect positive cases. While reverse transcriptase polymerase chain reaction (RT-PCR) test has an accuracy of around 90% (week 3 after symptoms) [1], the need to provide proper identification of affected people calls for alternate methods such as CT scans analysis, especially in hospitals that lack molecular tests1 but may have a CT scan readily available [2], thus mitigating said shortage. Medical professionals are resorting to this method to determine the presence of COVID-19 infection. Radiologists have reached an accuracy of around 90% with this method on low-dose CT scan [3]. Nevertheless, other studies suggest a lower accuracy, less than 80%, and a mean recall value of 80% [4]. Reliable artificial intelligence (AI) models have come to show accuracy levels higher than 80% in most cases as will be detailed later. However, most of these models require a huge amount of CT scans images to be trained on. Refs. [5] present a dataset collected from different data sources and proposes a model with an accuracy of 89%.

AI’s performance and benefits in medicine have been demonstrated time and again [6]. Transfer learning, widely used for pattern recognition tasks, has been recently applied to design intelligent systems capable of accurately identifying COVID-19 patients through CT Scan imagery. Ref. [7] developed artificial intelligence algorithms to identify positive COVID-19 patients by combining CT imaging and clinical information reaching an accuracy of 83.5%. Additionally, Ref. [8] proposed an AI system that can diagnose novel coronavirus pneumonia to assist radiologists performing diagnosis, achieving 92.49% accuracy on the test set. Regarding ensemble methods, one approach used chest X-Ray images to develop a transfer learning-based ensemble classifier for pneumonia identification. The authors emphasize the higher performance achieved by these when compared to individual models [9]. A similar approach for COVID-19 identification was developed, also showing significant results, on ensemble techniques [10].

The advantages of using ensemble methods are analyzed and discussed in this article. By exploring the differences in performance levels between soft, hard and weighted voting schemes, we demonstrate the superior accuracy provided by a weighted voting scheme, which resembles a generalized linear model with a binomial link function. Additionally, valuable findings were obtained while tuning the decision threshold. We found evidence of a performance boost in reducing the decision cut-off point by less than 0.05. Moreover, the use of raw output scores, instead of a binary classification, was found to be more effective by enabling the prioritization of critical cases and setting a risk status for cases near the threshold.

Starting with the results by Ref. [5]; this work expands on the use of transfer learning and ensemble methods to achieve three main tasks. (1) Build a model using transfer learning technique on state-of-the-art ImageNet pretrained models combining them into an ensemble than can be easily replicated by researchers and deep learning practitioners that may benefit from the current work helping to fight the novel coronavirus outbreak. (2) Achieve competitive performance by reaching an accuracy of at least 85%. (3) Present the limitations of dealing with small datasets in visual recognition tasks and expanding on how to overcome them.

2. Dataset

The dataset used in this research was provided by Ref. [5]. The authors who provided the dataset collected 746 CT scan images, composed by 349 COVID-19 positive and 397 COVID-19 negative images. We would like to emphasize the diligence in the aforementioned authors’ work in manually selecting images from 760 medRxiv and bioRxiv COVID-19 preprints posted from Jan 19th to Mar 25th. For each CT image, the associated caption was read to judge whether it was a positive case for COVID-19 or not. If caption was not available, this was inferred from the text analyzing the image. As images that are included in papers experience a degradation in their quality, the images gathered from papers were used for training, while original CT images donated from hospitals were used for testing and validating the model.

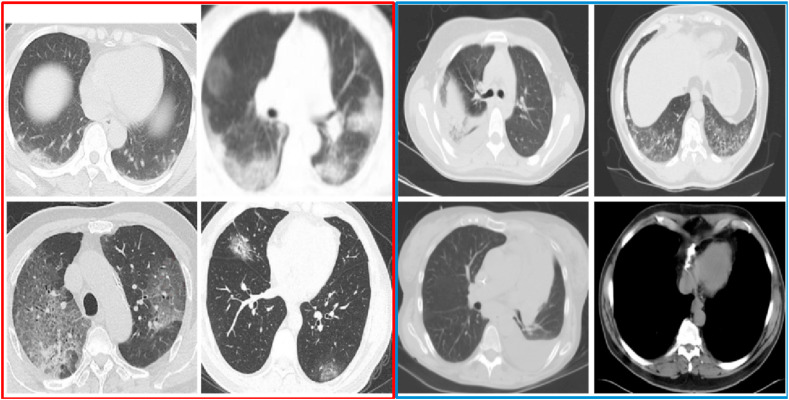
Table 1 shows the number of images in each set and class and Fig. 1 shows 8 randomly chosen samples. We will be using the same data split as proposed by the authors.

Table 1.

CT scan images distribution.

	COVID-19	NON-COVID-19	Total
Train	191	234	425
Validation	60	58	118
Test	98	105	203
			746

Fig. 1.

Sample of CT Scan Images. Images on the left, within the red border, are positive COVID-19 cases. Images on the right, within the blue border, are negative COVID-19 cases. Ground-glass opacities are usually found in positive COVID-19 cases. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

3. Methods and techniques

3.1. Data preparation

As deep neural models require a great amount of training data, pattern recognition models are not an exception. Since CT scan images do not suffer generally from rotation or vertical flips, we took as transformations random resized crop and random horizontal flip. The first one randomly selects a multiplier (from 0.08 to 1) to apply to the original size to select the cropping window size and an aspect ratio (from 0.75 to 1.33) before being resized. Random horizontal flip randomly flips horizontally an image with a probability of 0.5.

Besides data augmentation, it is important to preprocess images to specific parameters as previously trained models are optimized for data normalized in a specific range. For this reason, images are resized to 256 ​× ​256 pixels to be later resized to 224 ​× ​224 in the random resized crop transformation. Finally, images are normalized from 0 to 1 by dividing their pixel channels’ values by 255 (RGB 8-bit images are represented by pixels values ranging from 0 to 255 on each of their 3 channels). To keep original quality of validation and test set, images were only resized and standardized, with no augmentation involved.

The selection of the data augmentation methods presented are based on the proven effectiveness and the simplicity in interpretation of such methods [11]. Also, as we do not expect images to be presented, for example, with a 90° rotation or with sharp variations in brightness or contrast, such transformation techniques could lead to an increase in irrelevant augmented data. Finally, the parameters from the transformations are the ones commonly used in pretrained models such as Inception v3.

3.2. Model architecture

Our model is comprised of a 2-stage transfer learning training process and a stacked ensemble method. For this we used six ImageNet pretrained convolutional neural networks: VGG16 [12], ResNet50 [13], Wide ResNet50-2 [14], DenseNet161, DenseNet169 [15] and Inception v3 [16]. The classifier and fully connected layers are replaced by custom build layers. Specifically, VGG16 (with batch normalization) last fully connected layer was replaced by a layer consisting of 128 neurons with ReLU activation and a 0.5 dropout rate2 before being finally connected to a single neuron, responsible for the binary classification. Remaining neural networks had their fully connected top layer completely replaced by layer consisting of 256 neurons (except for the case of the DenseNet161 model which was initially fully connected to a layer containing 512 neurons) followed by a single dimension batch normalization function, ReLU activation and 0.5 dropout rate. Finally, output is connected to a layer consisting of 64 neurons with ReLU activation and 0.4 dropout rate to fully connect them to the decision neuron. It is important to underline the usage of the batch normalization layer. Batch normalization not only speeds up the training process and improves model generalization, but also helps reduce sensitivity to bad parameters initialization which could undermine models’ training process [17]. Table 2 shows the different classifier architectures per pretrained model.

Table 2.

Fully connected layer architecture. The VGG16 model shown architecture is added to the pretrained sixth layer in the classifier block.

VGG16		DenseNet161		ResNet50, Wide ResNet50-2, DenseNet169, Inception v3
Layer	Parameter	Layer	Parameter	Layer	Parameter
Linear	128 neurons	Linear	512 neurons	Linear	256 neurons
ReLU	–	ReLU	–	ReLU	–
Dropout	rate ​= ​0.5	Dropout	rate ​= ​0.5	Dropout	rate ​= ​0.5
Linear	1 neuron	Linear	64 neurons	Linear	64 neurons
		ReLU	–	ReLU	–
		Dropout	rate ​= ​0.4	Dropout	rate ​= ​0.4
		Linear	1 neuron	Linear	1 neuron

Ensemble models have the advantage of leveraging the information from several classifiers and combining them into a more robust model. Variance and bias are also reduced, thus minimizing the expected error. Additionally, a feature space region that may have been incorrectly learned by a classifier can still be correctly classified by using the pattern learned from another classifier, leveraged by the ensemble model. These characteristics make ensemble models a solid option for approaching complex classification and regression tasks [11].

These configurations of classification layers were chosen after performing hyperparameter optimization runs, this includes the number of neurons per layer (powers of two) and dropout rate. It was found that more than two hidden layers led the model to overfitting. It is especially important to recall that the dataset has a low number of images to train on, making our model prone to overfitting. We also find it important to emphasize the difference in architectures between the pretrained models. The added layers are defined as the classification block of the neural network; that is, they are fed by the final pooling layer on each neural network. One difference, as shown in Table 2, is that the VGG16 model has a shorter configuration. This is due to the fact that the added layer is actually part of a larger pretrained classification block (consisting of more than one layer) and a deeper block would make the model prone to overfitting. The remaining pretrained neural models have a single layer as part of their classification block, this is why we replaced the whole block with the proposed configuration. Regarding the number of neurons, we aimed to keep the second to last layer as small as possible without any reduction in performance, further avoiding overfitting.

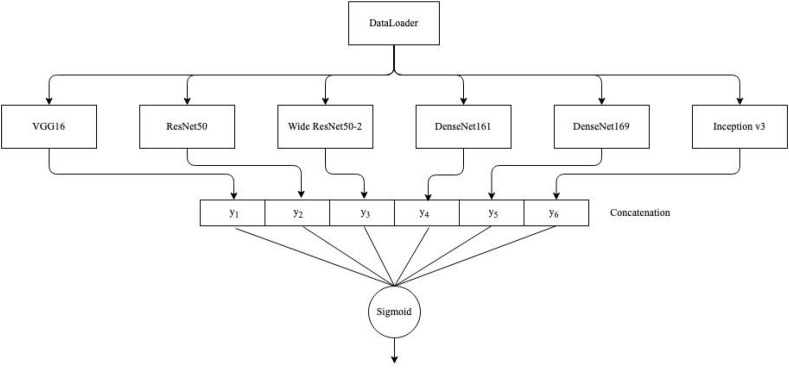
Finally, as shown in Fig. 2 , we concatenate outputs from each model to create a stacked ensemble model. Since each output is a single node, we are now left with a 6-dimensional vector which is connected to a single neuron activated by a sigmoid function. Training runs with one and two hidden layers comprised of 6 and 16 neurons were held, only to show a clear overfitting of the ensemble model.

Fig. 2.

Proposed model architecture. Variables y_k, where $k\in \left\{\mathrm{1,2,3,4,5,6}\right\}$, represent the outputs for each of the pretrained models.

3.3. Model training

As mentioned earlier, the proposed model was trained on a 2-stage process detailed by Algorithm 1. First, each pretrained model was replaced by the previously mentioned architecture, their feature’s layers were frozen, leaving only the fully connected layers available for training, and parameters were randomly initialized by He uniform initialization [18]. This model configuration was trained for 30 epochs in its first stage. An epoch refers to one whole training cycle through the training set. Within each epoch, the data is fed by batches. Once all of the batches are fed and training is executed, an epoch is completed. Immediately after, the second stage, also known as fine tuning, unfreezes the whole model and trains it for 20 epochs (Inception v3 model was trained for 30 epochs due to higher complexity and overall demonstrating better performance). Neural networks are fed by batches for training and testing, preprocessing3 and feeding them to the neural networks with a batch size of 32 images. As a single output node for binary classification activates a sigmoid function, the loss function is binary cross entropy. A two-stage training method helps prevent the randomness from the initialization in the output fully connected layer to disrupt the already learned parameters from the pre-trained models. This is done by allowing those parameters to be only fine-tuned after the first stage has optimized the output layer.

Algorithm 1

Individual models training algorithm

Algorithm
Input:	COVID-19 CT Scan Images dataloader_batch
Preprocessing:
	If set is training_set:
		Resize image to dimensions (256 ​× ​256)
		Random crop and resize to dimensions (224 ​× ​224)
		Perform random horizontal flip
		Normalize pixel values to [0, 1] range
		Standardize pixel values
	Else:
		Resize image to dimensions (224 ​× ​224)
		Normalize pixel values to [0,1] range
		Standardize pixel values
	Endif
Models training:
Models ​= ​{VGG16, ResNet50, Wide ResNet50-2, DenseNet161, DenseNet169, Inception v3}
For model in Models:
	Freeze feature layers
	lr ​= ​1e-3
	For epoch ​= ​1 to 30:
		For img in dataloader_batch:
			Update model parameters
		End
		If validation_accuracy does not improve for 10 epochs then:
			lr ​= ​lr x 0.1
		End
	End
	Unfreeze feature layers
	lr ​= ​1e-4
	For epoch ​= ​1 to 20:
		For img in dataloader_batch:
			Update model parameters
		End
		If validation_accuracy does not improve for 10 epochs then:
			lr ​= ​lr x 0.1
		End
	End
End
Output: Trained models

Regarding the optimizer for ensemble model, the method used included the Adam algorithm with decoupled weight decay [19], also known as AdamW optimizer. It has been proven that the Adam optimizer with L2 regularization4 generally fails to converge to a global optima, since its regularization term fails to be equivalent to weight decay as in Stochastic Gradient Descent (SGD) optimization, instead converging quickly and uniformly to a local optima. This is why the SGD with momentum optimization has been the optimizer of choice for many state-of-the-art neural networks. On the other hand, the AdamW optimizer correctly adds the weight decay after the moving averages are calculated. This greatly prevents models to overfit (the model no longer being able to generalize enough to accurately predict from new data), especially when dealing with small datasets.

Learning rate was set to 1e-3 for the first stage and 1e-4 for the second stage, to account for fine tuning, avoiding taking large gradient descent steps to prevent feature layers values from varying significantly. This is one of the most important hyperparameters in neural networks: learning rate controls how much the model’s parameters are updated in response to the network’s error. Selecting a proper learning rate is of utmost importance since a value too high could cause the objective function to diverge while a value too low could make learning too slow and the loss function could converge to a local optimum. To ensure a more robust control of the learning network, we set a learning rate scheduler for both stages, based on validation accuracy behavior, with a patience value of 10 and a reduction factor of 0.1. In this way, when the training reaches a point in which after 10 epochs no improvement is seen, the learning rate is reduced to 10% of its original value. This further improves the training, avoiding overfitting by gradually reducing learning rate when the increase in validation accuracy seems to have come to a stall.

It is important to note that we tested cosine annealing learning rate scheduler on both SGD with momentum [20] and AdamW optimizers, but found no significant improvements over the initial learning rate scheduler. Further testing on these schedulers and optimizers combination is recommended to properly find evidence (or lack thereof) for improvements under the trained dataset. Finally, to avoid training for excessive epochs, we set a best model checkpoint based on validation accuracy for the second stage, this way the trained parameters which led to the highest validation accuracy while training, are the ones used by the model once the training is over.

The aforementioned training specifications were applied to each of the six individual models. Finally, after the second stage is completed, outputs concatenated and all models frozen, the ensemble single output neuron is trained for 15 epochs, using an AdamW optimizer, learning rate of 1e-3 and best model checkpoint. It is important to note that while some initializations required the model to be trained on more than 15 epochs to reach convergence, most of the time it was quickly achieved within the first 10 epochs.

To test this model against an ensemble baseline, we built a voting classifier based upon the results from the six models. For this, we provided two voting methods: hard voting, in which final class label is predicted by a majority rule voting of all six estimators predicted labels; and soft voting, where scores from all six estimators are averaged and rounded to the nearest integer to give out the final prediction [11]. In both methods, a progressive validation of estimators in an ensemble was produced: models were sorted, based on their validation accuracy from highest to lowest, and their ensemble’s new accuracy was registered. The highest validation accuracy ensemble was selected, and performance metrics were calculated on the holdout test set.

The proposed model was trained on an instance with 61 ​GB RAM, four Intel Xeon vCPU running at 2.7 ​GHz and one NVIDIA K80 GPU with 12 ​GB of memory. Deep learning library PyTorch was used for data preprocessing and model training on Python 3.6.6.5

4. Experimental results

Initial hyperparameters for models, including construction of fully connected layer, number of epochs per stage, learning rate, scheduler configuration and optimization method, were found through controlled iterations on each model based on reported final performance on the validation set.

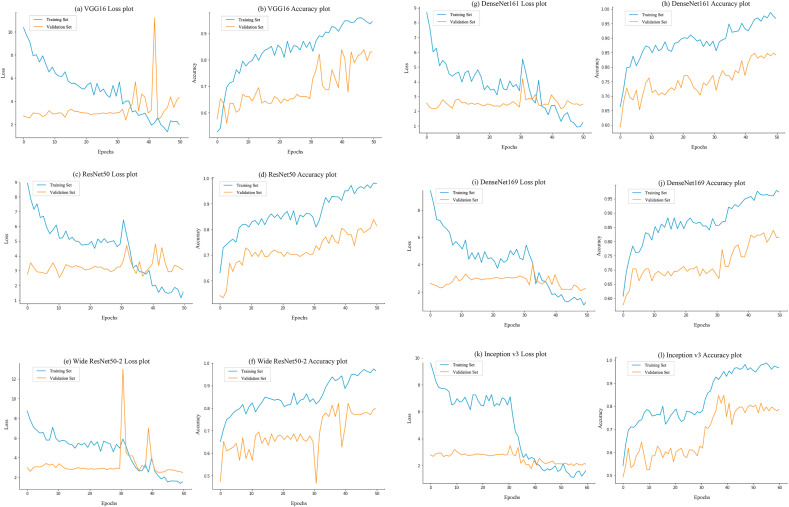
The metrics recorded to evaluate our model’s performance were accuracy, recall, specificity, precision, F1 score and area under the ROC curve (AUC) [21]. Accuracy and loss plots (see Fig. 3 ) show interesting results when combining the two stages in a single plot. Both plots show the evolution of accuracy and loss on each epoch. These plots are used while training a neural network to assess the fitting behavior of the model. For example, a model with a validation accuracy plot which stops increasing, while the training set’s accuracy continues to increase, can be evidence of overfitting. This kind of behavior should be avoided by the use of generalization techniques such as the ones previously described. As soon as the second stage starts, both training and validation accuracy show a performance bump of around 10% on average, this can be explained by the fine tuning of the pretrained feature layers adjusting to the new layers. However, loss plots show a different behavior. Training loss shows a decrease of up to 70% when comparing convergence achieved in the first versus the second stage. Nevertheless, validation loss shows little evidence of decreasing, remaining almost stationary during training. This is due to the scarcity in validation data, where scores near the decision threshold (0.5) are correctly adjusted at the expense of highly confident correct scores nearing the threshold, farther away from the true label. Binary cross entropy loss function penalizes higher differences between model output and true value more strongly, due to the log function behavior. For example, for a positive label sample, a change in model output from 0.45 to 0.55 represents a decrease of 0.09 in loss and an increase in accuracy of almost 1%, while a change in model output from another positive sample from 0.9 to 0.7 means an increase of 0.10 in loss with no change in accuracy. Changes in individual samples have a more profound effect when dealing with small validation sets.

Fig. 3.

Loss and accuracy plots of pretrained models training. These plots expose the accuracy bump right after the second stage starts at epoch number 30. Although there seems to be evidence for overfitting behavior in the Inception v3 model (l), the remaining plots show little evidence of it, as the validation accuracy demonstrates an increasing tendency. Overfitting is further avoided by the use of model checkpoints, which are specifically useful in the Inception v3 model.

As it can be seen from Fig. 3, the second stage was key to reach the performance levels achieved. At this point, the pretrained model parameters are finely adjusted along with the classification block which was already trained in the first stage. This allows for each of the ensemble models to shift from the pretrained classes to the new classes, by learning the features from the latter ones. The effect is finally reflected on the performance increment obtained.

Table 3 shows the metrics for each of the six models, the ensemble baseline model and the proposed model. As we can see, although the best of the six pretrained models, based on accuracy is DenseNet161 deep convolutional neural network, the ensemble soft-voting baseline method fails to overcome performance metrics from the best pretrained model. Moreover, the ensemble hard-voting baseline method yields less encouraging results, remaining 0.5% below the soft-voting ensemble. It is important to bear in mind that this voting scheme averages the scores from each model, thus giving an equal weight to each of these. We can infer that, to make the soft-voting method at least as good as the single best pretrained model, a weighted average should be taken into account. This leads us to the proposed model previously described, where besides applying a weighted average with an offset constant, the final result is normalized by a sigmoid function.

Table 3.

Models’ performance metrics.

Models	Accuracy	Precision	Recall	Specificity	F1 Score	AUC
VGG16	81.77%	79.05%	84.69%	79.05%	81.77%	90.15%
ResNet50	78.82%	80.22%	74.49%	82.86%	77.25%	87.19%
Wide ResNet50-2	81.77%	79.61%	83.67%	80.00%	81.59%	88.07%
DenseNet161	82.76%	85.39%	77.55%	87.62%	81.28%	89.56%
DenseNet169	80.79%	81.05%	78.57%	82.86%	79.79%	89.44%
Inception v3	80.30%	79.59%	79.59%	80.95%	79.59%	88.80%
Ensemble (Hard voting)	81.77%	82.80%	78.57%	84.76%	80.63%	–
Ensemble (Soft voting)	82.27%	83.70%	78.57%	85.71%	81.05%	90.01%
Proposed Model	86.70%	88.17%	83.67%	89.52%	85.86%	90.82%

Since this is a binary classification model, confidence intervals with a confidence level of 95% by binomial proportion are obtained following the Wilson method [22], as shown in Table 4 . AUC confidence intervals are determined using the DeLong method [23].

Table 4.

Confidence intervals for models’ performance metrics with a 95% confidence level.

Models	Accuracy	Precision	Recall	Specificity	AUC
VGG16	[75.89, 86.48]	[70.31, 85.74]	[76.27, 90.50]	[70.31, 85.74]	[85.81, 94.49]
ResNet50	[72.69, 83.88]	[70.89, 87.11]	[65.05, 82.08]	[74.52, 88.87]	[82.40, 91.98]
Wide ResNet50-2	[75.89, 86.48]	[70.83, 86.26]	[75.11, 89.69]	[71.35, 86.53]	[83.00, 93.13]
DenseNet161	[76.97, 87.33]	[76.60, 91.26]	[68.34, 84.68]	[79.96, 92.62]	[85.07, 94.06]
DenseNet169	[74.82, 85.62]	[72.03, 87.67]	[69.45, 85.54]	[74.52, 88.87]	[85.18, 93.69]
Inception v3	[74.28, 85.18]	[70.57, 86.38]	[70.57, 86.38]	[72.40, 87.32]	[84.16, 93.45]
Ensemble (Hard Voting)	[75.89, 86.48]	[73.87, 89.12]	[69.45, 85.54]	[76.67, 90.40]	–
Ensemble (Soft Voting)	[76.43, 86.91]	[74.83, 89.86]	[69.45, 85.54]	[77.76, 91.15]	[85.69, 94.33]
Proposed Model	[81.34, 90.70]	[80.05, 93.27]	[75.11, 89.69]	[82.21, 94.05]	[86.61, 95.02]

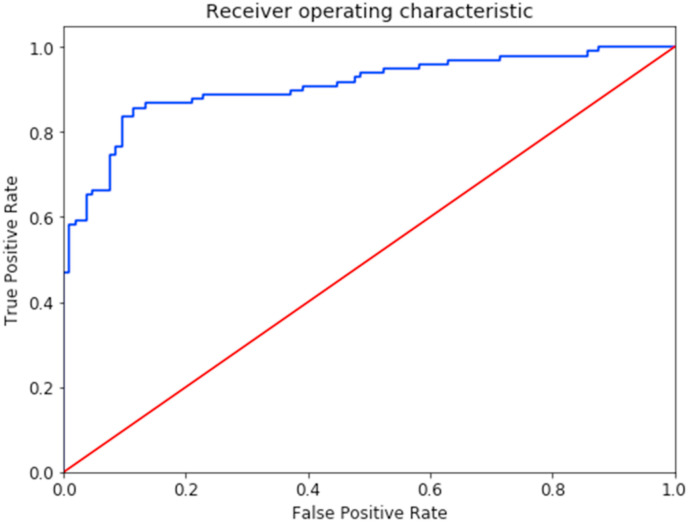
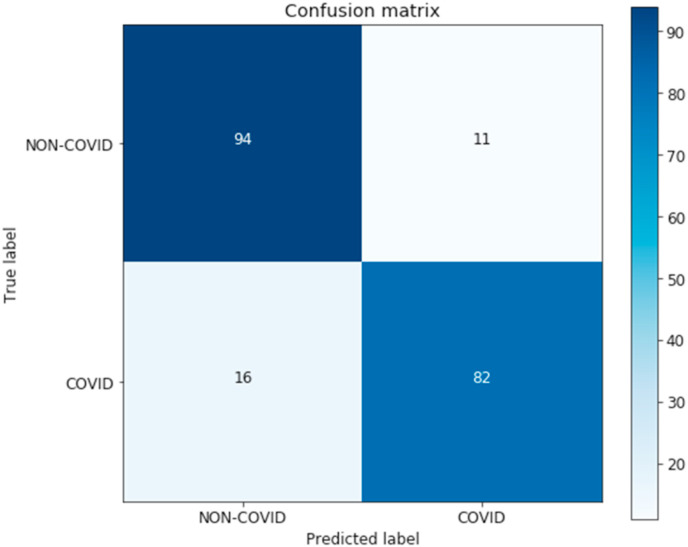
Further experimentation on raw model output, before the classification threshold is applied, showed interesting results when setting a slightly greater range for positive classification. As the raw output is the product of a logistic regression, it can also be used to assess patients at risk of being infected, considering patients with a score slightly below the threshold of 0.5 to be possible COVID-19 positive. Furthermore, setting the classification threshold to 0.45 yields an accuracy of 87.19%, a precision of 87.50%, a recall of 85.71%, a specificity of 88.57% and an F1 score of 86.60%, proving that the use of a threshold range (scores from 0.45 to 0.5 being considered COVID-19 risk cases) can improve model performance, including recall, to increase beyond any previous models. For the present article we will be considering the standard threshold of 0.5 to avoid any bias by fine-tuning the classification cutoff point with the test set. Finally, the proposed model’s accuracy overcomes all other models’, reaching 86.70%. The ROC plot and confusion matrix are shown in Fig. 4 and Fig. 5 .

Fig. 4.

Receiver Operating Characteristic curve for the proposed stacked ensemble model. This plot measures the classification performance at various decision threshold values by showing the model’s ability at distinguishing both classes. As the blue curve gets closer to the upper and left-hand boundaries, the model shows a smaller Type I error. The red line illustrates the case in which the model is unable to tell one class from the other, being no better than classifying by chance. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

Fig. 5.

Confusion matrix for the proposed stacked ensemble model. The matrix describes the detailed test set performance of the classifier by comparing how each case was predicted against their true labels. From this matrix we can easily see that there are 94 true negatives, 11 false positives, 16 false negatives and 82 true positives.

4.1. Activation heatmap visualization

To better understand each convolutional model individually, we can identify the regions from CT scan images off of which the model was based to finally infer the label. Grad-CAM [24,25] is a technique which produces visual explanations for decisions by taking the values from the gradients in the model’s final feature layer, for highlighting the important regions taken by the model in their prediction.

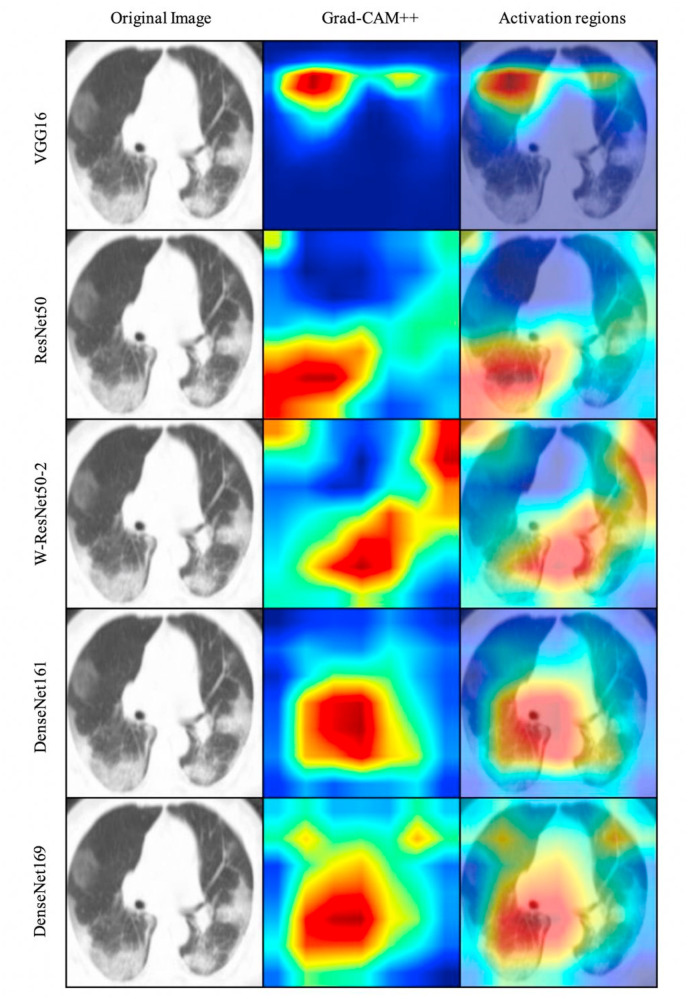
As can be seen in Fig. 6 , models often identify regions from the CT scan mainly described as hazy, “ground glass” white spots which are the main indication of the presence of COVID-19 in a patient. Although not in all cases, a model manages to resort to the correct regions for inference (as the VGG16 model on Fig. 6) the ensemble method we propose takes into consideration the decision of other models that, as an alternative, have been proven to detect correct regions from which to base their inference. For instance, while DenseNet161 and VGG16 were the best fitted models, based on accuracy and F1 score, the latter’s last layer is seen to be poorly activated by the sample presented, contrasting with other models which, working as an ensemble, provide the advantage of correctly boosting performance. Indeed, this specialization of some models to detect better certain CT scan images regions provides a robust classifier when ensembled into a stacked model: contribution from each output can be optimized to finally obtain a more accurate prediction by weighting each model’s output for each case to finally agree on a prediction.

Fig. 6.

Grad-CAM++ activation regions visualization for the first five pretrained models. The areas with higher intensity in the generated heatmap (second and third columns) are the ones with the highest activation response from the last convolutional layers on each pre-trained model. This provides a better human-interpretable explanation of the decisions taken by the classifiers.

Nevertheless, activation heatmaps are not only useful for model interpretation. Refs. [26] demonstrate a useful application for activation heatmaps in discriminative localization. In their research they show a CNN activation heatmap effectively localizing specific image regions, based on the classification classes. This feature can be used by physicians to not only detect positive COVID-19 cases, but to also infer the affected region. By having a visual interpretation of the classification results, as seen in Fig. 6, physicians could avail themselves of this information to focus treatment in the affected area. Moreover, this could potentially be used in further investigation of the effects COVID-19 has in the human body.

5. Discussion

In this study, an ensemble deep learning architecture was used to design a classifier to diagnose COVID-19 cases following a 2-stage algorithm. Our findings now provide evidence that support the superior results yielded by the use of an ensemble approach. It can be inferred from the models’ performance metrics (Table 3) that the proposed ensemble model outperforms each of the single pre-trained models. Furthermore, voting ensemble models were developed and showed that there is not enough evidence that regular hard and soft voting ensembles best the individual pre-trained models. It is important to note that the main difference lies in the fact that the proposed model assigns coefficients to each of the pre-trained models’ outputs in the same way as a generalized linear regression model, following a binomial link function, does. This allows the ensemble to assign weights to each pre-trained model based on their own effectiveness. Despite the fact that we didn’t expect the regular voting ensemble method to fail to outperform the individual models, it revealed the effect that weighted coefficients applied to each output had.

Most of the studies that motivated the present research demonstrated similar accuracy levels with different architectures (Table 5 ). Ref. [27] proposed a M-Inception model to diagnose COVID-19 from CT scan images achieving an accuracy of 82.9% dealing with a limited dataset. Ref. [28] developed a model capable of distinguishing COVID-19 from viral pneumonia and healthy cases, reaching an accuracy of 86.7%. Ref. [29] designed a Details Relation Extraction neural network (DRE-net) built on a ResNet-50 structure which achieved an accuracy of 86%. Additional approaches that combined clinical information also were found to reproduce competitive results. Ref. [7] combined CT imaging and clinical information to reach an accuracy of 83.5%. Furthermore, overall our method was the one that obtained superior performance in terms of accuracy, compared to other studies in the literature.

Table 5.

Comparison of the proposed model with other deep learning algorithms developed using CT Scan images.

Algorithm Design	Dataset	Accuracy (%)	Reference
M-Inception	Positive cases: 195	82.90%	[27]
	Negative cases: 258
ResNet	Positive cases: 219	86.70%	[28]
	Negative cases: 175
	Viral Pneumonia: 224
DRE-Net	Positive cases: 777	86.00%	[29]
	Negative cases: 708
Joint Model	Positive cases: 419	83.50%	[7]
	Negative cases: 486
Ensemble model	Positive cases: 349	86.70%	Proposed method
	Negative cases: 397

Recall metric provides us a way to measure and understand the model’s capacity to correctly identify positive COVID-19 patients. This metric is of much importance given that each false negative can have a detrimental effect on the patient’s health, rendering him or her as healthy, while actually being infected. Although the proposed model achieves a lower recall than the VGG16 model, this comes at a bigger cost for the latter: precision and specificity abruptly fall below 80%. On the other hand, the proposed model reaches an 89.52% level of specificity, reducing the occurrences of false positives. Whereas a higher recall is desired, since the reduction of false negatives is of primary concern to adequately identify all COVID-19 cases, the proposed model achieves a considerably greater increase in precision and specificity. We will exemplify how with absolute values from the test set: the decrease of 1% in recall and increase of 10.5% in specificity can be understood as 1 less positive COVID-19 case correctly identified, while 11 more negative COVID-19 cases are correctly classified. This evidenced the importance of recall-precision trade-off analysis even in cases where false negatives need to be diminished.

Our findings on the use of a threshold range for classification revealed an increase in the proposed model’s performance. Reducing the classification threshold by as little as 0.05 boosted the performance significantly, increasing recall to over 85%. This evidences that the use of raw output scores can be effectively used to adequately prioritize high risk patients.

One of the main limitations of the present research was the small dataset available. The results show that despite of this limitation, our proposed model was capable of achieving an accuracy level over 85% by the use of techniques such as regularization, learning rate schedulers and data augmentation agreeing with the existing literature. [31] compares the difference of using transfer learning with augmented data versus non-augmented data within the same dataset. The authors found that data augmentation proved to increase model accuracy in four out of the five models tested. Although these methods helped the model to avoid overfitting, one of the pretrained models, Inception v3, showed an overfitting pattern on its accuracy plot (Fig. 3). However, the model checkpoint implementation retrieved the parameters before the overfitting took place.

Another limitation of this study was the fixed dataset split configuration used. As described in the Dataset section, images gathered from papers were used for training and original CT scan images donated from hospitals were used for testing and validating the model. This prevented us from applying cross-validation to construct confidence intervals for the performance metrics. Nevertheless, we determined confidence intervals from binomial classification, as shown in Table 4, providing statistical significance to the metrics obtained.

Lastly, although procedures already exist for proper identification of brain or lung injuries by CT scan, this is not the case for COVID-19, being the reason why PCR tests are preferred for such diagnosis. Nevertheless, in the absence of said tests, diagnosis by CT scan is possible and accurate, when combined with information from the patient’s medical history. This assessment was supported by a radiologist, confirming the effectiveness of the proposed model in hospitals suffering from a shortage of test kits.

Future research should focus on the use of ensemble methods as a way to enhance state-of-the-art architectures’ performance. Although several advances in neural networks for COVID-19 diagnosis have been made, an ensemble method would lead to a boost in performance, which could become significant. Also, as more data is generated, training should be performed on a larger number of samples, helping overcome one of the limitations mentioned in this article, and leading to a more robust classifier that could be deployed and made publicly available for hospitals that are lacking PCR tests to effectively provide a COVID-19 diagnosis.

6. Conclusions

With the novel coronavirus outbreak now a global threat, the timely identification of positive COVID-19 cases became of main concern, helping ensure early treatment and proper pandemic control. The use of transfer learning and ensemble architectures for training artificial neural networks, as presented in this paper, provided a sound and effective method for detecting COVID-19 cases based on chest CT scan images.

Although state-of-the-art pretrained models are capable of attaining high performance, the addition of ensemble methods has proven to boost models’ metrics. The proposed model achieved performance levels above those reached by radiologists [3,4], and are competitive with current literature’s artificial intelligence models, ranging from 80% to 90% in most cases, proving its effectiveness. We trained six pre-trained ImageNet models in two stages, feeding each classifier with a dataset comprised of 746 CT scan images, 349 being COVID-19 positive and 397 being COVID-19 negative. The ensemble was finally built by concatenating the models’ outputs into a final activation neuron. We found that the use of threshold ranges to assess the risk of a COVID-19 positive case yields a higher performance without reducing specificity and precision. We also found important to emphasize the added potential capacity of automatizing CT scan analysis, greatly reducing its lead time and giving out a probability of COVID-19 presence for the patient. This, enhanced by integrated applications, could speed up COVID-19 testing, providing results in a very small timeframe and deriving only scores close to classification boundary to a specialist.

If we cannot provide timely and proper COVID-19 diagnosis, our efforts to hinder the expansion of the coronavirus could be thwarted. This is especially relevant in developing countries where shortages of PCR test kits can disrupt the efforts to combat the pandemic. We encourage researchers in artificial intelligence to further improve on current literature’s methods, contributing in a joint effort to combat the novel coronavirus pandemic.

Declaration of competing interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.