The most efficient metazoan swimmer creates a ‘virtual wall’ to enhance performance

Abstract

It has been well documented that animals (and machines) swimming or flying near a solid boundary get a boost in performance. This ground effect is often modelled as an interaction between a mirrored pair of vortices represented by a true vortex and an opposite sign ‘virtual vortex’ on the other side of the wall. However, most animals do not swim near solid surfaces and thus near body vortex–vortex interactions in open-water swimmers have been poorly investigated. In this study, we examine the most energetically efficient metazoan swimmer known to date, the jellyfish Aurelia aurita, to elucidate the role that vortex interactions can play in animals that swim away from solid boundaries. We used high-speed video tracking, laser-based digital particle image velocimetry (dPIV) and an algorithm for extracting pressure fields from flow velocity vectors to quantify swimming performance and the effect of near body vortex–vortex interactions. Here, we show that a vortex ring (stopping vortex), created underneath the animal during the previous swim cycle, is critical for increasing propulsive performance. This well-positioned stopping vortex acts in the same way as a virtual vortex during wall-effect performance enhancement, by helping converge fluid at the underside of the propulsive surface and generating significantly higher pressures which result in greater thrust. These findings advocate that jellyfish can generate a wall-effect boost in open water by creating what amounts to a ‘virtual wall’ between two real, opposite sign vortex rings. This explains the significant propulsive advantage jellyfish possess over other metazoans and represents important implications for bio-engineered propulsion systems.

1. Introduction

The phenomenon of increased lift generated over static surfaces moving parallel to a solid boundary is termed ‘steady ground’ or ‘steady wall’ effect. This process has been previously studied and reviewed [1] leading to literature describing the advantages in air [2–5] and water [6,7]. The increase in lift near the ground is largely attributed to decelerated flow beneath the lifting surface resulting in higher underside pressures. This effect is often modelled as an interaction between a mirrored pair of vortices represented by a true vortex and an opposite sign ‘virtual vortex’ on the other side of the wall [8]. More recently, it has been shown that considerable performance benefits also exist for non-static, active swimming near a solid boundary. For example, swimming animals exhibit the reduced cost of transport and improved energetic efficiencies when near a wall [9,10] as well as a 25% increase in speed and 45% increase in thrust near a solid surface [11]. Therefore, the increase in the lift for a static propulsor translates to an increase in thrust in the unsteady case [12,13]. However, this phenomenon has not been explored for unsteady propulsors away from solid boundaries even though numerical models have suggested true vortex–true vortex interactions can, under the right circumstances, produce an equivalent effect. Thus, the question we address in this study is: are there free-swimming species that produce the appropriate vortex–vortex interactions for a wall-effect type boost in performance?

As a taxonomic group, jellyfish have been swimming the world's oceans for over 500 million years [14] and are the most energetically efficient swimmers known to date [15,16]. Their high performance relies on generating effective body-fluid interactions despite having muscle tissue that is only a single-cell mono-layer in thickness [17,18]. The ability to generate sufficient thrust with very low-power input makes medusae an intriguing target for elucidating the role of body kinematics and resulting fluid interactions. Other characteristics of medusan swimmers such as their axisymmetric morphology, translucent body tissues and consistent swimming kinematics make them an ideal animal model to investigate questions of body flexibility, vortex interactions and their roles in generating favourable pressure fields for thrust.

Earlier work on jellyfish locomotion recognized that vortex formation (i.e. starting and stopping vortices) plays an important role in rowing-based medusan propulsion [17,19–21] but the mechanistic underpinnings of the vortex–vortex interactions and the resulting impact on thrust generation were not well understood. However, more recent work demonstrated that jellyfish can use passive energy recapture (PER) of the stopping vortex [16], allowing the moon jellyfish (Aurelia aurita) to gain an additional 30% more distance per swim cycle without the input of additional energy. This PER is accomplished by the enhancement and repositioning of a stopping vortex during the refilling (i.e. recovery) phase of the swim cycle by the flexible margin of the medusa bell [22]. The jellyfish then pauses before the next swimming contraction, and the induced flow of the stopping vortex ring creates a high-pressure region at the subumbreallar surface, thereby contributing additional thrust to move the animal forward [16]. The previously unrecognized importance of the stopping vortex is likely due to the fact that this vortex ring remains obscured within the medusan subumbrella until the contraction of the jellyfish bell occurs and the remnants of stopping vortex are ejected with the starting vortex, which has merged into a laterally oriented vortex superstructure [23].

The use of the stopping vortex to gain additional distance each swim cycle is widespread in medusae [24]. We have previously shown that while the concealed stopping vortex allows jellyfish to travel greater distances each swimming cycle, the overall benefit in terms of distance travelled primarily depends on the pause duration before the next cycle of bell contraction begins. It should be noted that across a diverse array of jellyfish taxa, the jellyfish begins the next swimming cycle well before the stopping vortex dissipates [16,24]. Thus, the maximum potential of the stopping vortex is not fully exploited and therefore limits the overall distance gained through the PER mechanism. It has remained unclear why this occurs and why jellyfish do not take full apparent advantage of the stopping vortex.

Jellyfish represent an intriguing target for investigations of open-water vortex–vortex interactions as they are the most energetically efficient swimmers known to date [15,16] and have a variety of traits that make them ideal organisms for fluid dynamics work. While many aspects of jellyfish swimming have been investigated (figure 1), observations of fluid interactions directly underneath the animal at the subumbrellar surface are very difficult to observe fully (even though the tissues are translucent) and have yet to be explored. In this study, we specifically target this area using advanced techniques to explore the role that vortex–vortex interactions play in medusan swimming. We demonstrate a previously undescribed role of the stopping vortex with respect to its ability to enhance thrust and swimming performance as it interacts with another vortex ring to generate a ‘virtual wall effect’. The result is a significant increase in overall swimming performance and may also have important implications for understanding feeding in medusae, locomotion in other taxonomic groups as well as informing design principles for the engineering of bioinspired vehicles.

Figure 1.

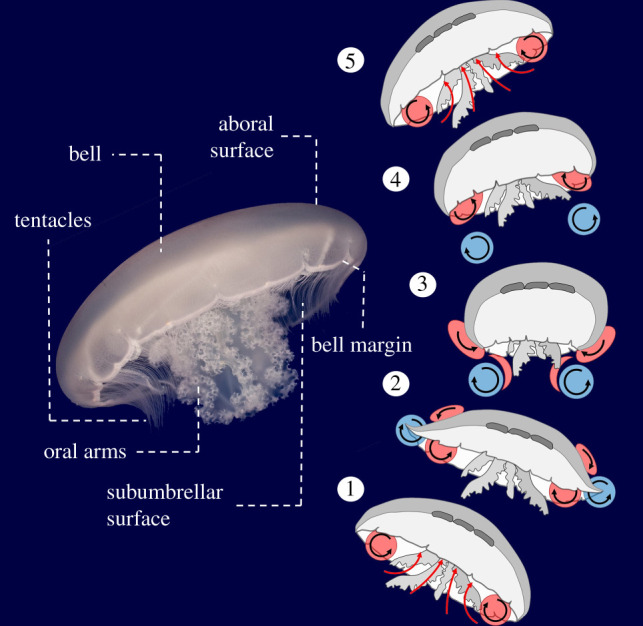
Anatomical features of a jellyfish and the vortex arrangement over the course of a swim cycle for the moon jellyfish (Aurelia aurita). Red = stopping vortex, blue = starting vortex. Black arrows = direction of fluid circulation. (1) and (5) Passive energy recapture mechanism (Gemmell et al. [16]). (2) Utilization of suction thrust from the upstream stopping vortex (Colin et al. [25]; Gemmell et al. [22]). The significance of the early stages of vortex–vortex interactions at the subumbrellar surface has not been investigated and is the focus of the present study. (3) Completion of the bell contraction. The starting vortex travels downstream in the wake after cancellation of the stopping vortex (Dabiri et al. [17]). (4) The stopping vortex is enhanced and repositioned inside the subumbrellar cavity (Gemmell et al. [22]). The newly formed stopping vortex and the downstream starting vortex interact to form a laterally oriented vortex superstructure (Dabiri et al. 2005 [23]). (Online version in colour.)

2. Methods

Jellyfish (Aurelia aurita) were obtained from the New England Aquarium and maintained in the laboratory in 20 l aquaria and fed with newly hatched Artemia salina nauplii daily. Free-swimming jellyfish between 3.8 and 4.2 cm in diameter (n = 8) were recorded in a glass filming vessel (30 × 10 × 25 cm) by a high-speed digital video camera (Fastcam 1024 PCI; Photron) at 1000 frames per second. Only recordings of animals swimming upward were used in the analysis to eliminate the possibility of gravitational force aiding the forward motion of the animal between pulses. Detailed kinematics (2D) were obtained using Image J v. 1.46 software (National Institutes of Health) to track the x and y coordinates of the apex of the jellyfish bell and the tips of the bell margin over time. Swimming speed was calculated from the change in the position of the apex over time as follows:

$$U=\frac{{({(x_2-x_1)}^2+{(y_2-y_1)}^2)}^{1/2}}{t_2-t_1}.$$ 2.1

Jellyfish were illuminated with a laser sheet (680 nm, 2 W continuous wave; LaVision) oriented perpendicular to the camera's optical axis to provide a distinctive body outline for image analysis and to ensure the animal remained in-plane, which ensures the accuracy of 2D estimates of position and velocity. Kinematic data were log-transformed and checked for normality using a Shapiro–Wilks test. Data were subsequently tested using one-way ANOVA to determine if a significant difference existed between means.

Fluid motion created by the jellyfish while swimming was quantified using two-dimensional digital particle image velocimetry. Using the setup described above, the filtered seawater was seeded with 10 µm hollow glass beads (Dantec Dynamics). The velocities of particles illuminated in the laser sheet were determined from sequential images analysed using a cross-correlation algorithm (LaVision software). Image pairs were analysed with shifting overlapping interrogation windows of decreasing size of 64 × 64 pixels to 32 × 32 pixels or 32 × 32 pixels to 16 × 16 pixels.

Pressure fields calculations were based on the queen 2.0 pressure field calculation package for MATLAB [26]. Pressure field data were inferred from the measured velocity fields by numerically integrating the inviscid Navier–Stokes equation, or Euler equation:

$$\mathrm{\nabla }p=\hspace{0.17em}-\rho \left(\frac{\mathrm{\partial }\text{u}}{\mathrm{\partial }t}+(\text{u}\cdot \mathrm{\nabla })\text{u}\right)=\hspace{0.17em}-\rho \frac{D\text{u}}{Dt},$$ 2.2

where ρ is the fluid density, p is pressure and u is the Eulerian velocity field. Details of this method are given in [25] and described briefly below.

The material acceleration term Du/Dt, which quantifies the acceleration of individual fluid particles in the flow, was calculated from the measured DPIV velocity field u(x, y). The pressure term was then determined to within a constant of integration by integrating equation (2.2) spatially. To reduce errors in the numerical integration of the measured velocity data, the procedure of Liu & Katz [27] was employed. Data were input on a time series of DPIV images on a 128 × 128 grid. Preprocessing of the DPIV data was completed in MATLAB to compute the material acceleration Du/Dt, which is also a required input to the pressure calculation code. Material acceleration was determined by computing the difference in the velocity of fluid particles initially located at the DPIV data grid points at time t₁ and subsequently advected to new positions time t₂ [25]. The output data from the code is a time series of pressure fields with scalar pressure computed at each of the 128 × 128 nodes of the corresponding DPIV fields.

3. Results

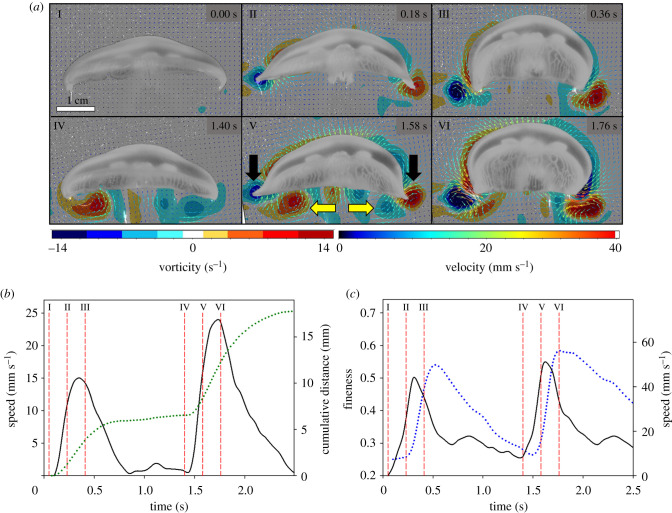
An important result that allows the direct comparison of fluid interactions in this study is the fact that medusae display no difference in kinematics (figure 2, table 1). This generation of consistent swimming kinematics whether starting from rest or already undergoing steady swimming provides a unique opportunity to explore the role of vortex interactions in biological propulsion. While kinematics did not differ, we observed significant performance differences in the swim cycles between animals beginning from rest and those already swimming (figure 2b, Table 1). Animals that were already swimming saw a 41% increase in maximum swimming speed and a 61% increase in cumulative distance travelled per swimming cycle compared to those starting from rest. This performance discrepancy is unlikely due to any differences in momentum between the two types of swimming cases as small A. aurita come to a stop (near zero forward velocity) at the end of each swimming cycle (figure 2b). This period lasts for approximately 0.5 s. Thus, whether starting from rest or during steady swimming, small A. aurita begin each new swim cycle with negligible forward momentum.

Figure 2.

Representative swimming sequence of a 4 cm moon jellyfish (Aurelia aurita) as it begins swimming from rest. (a) Fluid vorticity and velocity variables. Note the lack of vorticity under the bell in I and the presence of a stopping vortex prior the next second contraction cycle in IV. Black arrows show an example of the starting vortex and yellow arrows show the stopping vortex. (b, c) Kinematic and performance variables during two swim cycles shown in (a). Vertical dashed lines (red) denote the panel numbers in (a). (b) Swimming speed (solid black line) and cumulative distance (dotted line). (c) Bell fineness (blue dotted line) and instantaneous speed of the bell margin (solid line). (Online version in colour.)

Table 1.

Mean values for kinematic and performance metrics for the jellyfish Aurelia aurita in the presence or absence of a stopping vortex underneath the animal.

parameter	stopping vortex absent	n	stopping vortex present	n	p value
bell margin speed	56.3 (s.d. 4.2) mm s−1	6	58.7 (s.d. 4.4) mm s−1	8	0.439
bell fineness at peak contraction	0.549 (s.d. 0.05)	6	0.562 (s.d. 0.04)	8	0.677
contraction duration	441.7 (s.d. 7.5) ms	6	428.3 (s.d. 17.2) s	8	0.179
total displacement	7.9 (s.d. 1.9) mm	5	12.7 (s.d. 1.5) mm	7	*0.007
maximum swimming speed	18.2 (s.d. 1.5) mm s−1	6	25.7 (s.d. 0.9) mm s−1	8	*<0.001
maximum negative pressure	−0.34 (s.d. −0.11) Pa	5	−0.51 (s.d. 0.12) Pa	6	0.120
maximum positive pressure	0.32 (s.d. 0.09) Pa	5	0.74 (s.d. 0.08) Pa	6	*<0.001

Therefore, in jellyfish, the only notable difference between the two swimming cases is the presence or absence of a stopping vortex underneath the bell of the medusa. Individuals starting from rest display no vortices while large stopping vortices (mean maximum vorticity: 18 s⁻¹ s.d. 4) were evident for individuals that had just completed a swimming cycle (figure 1). This stopping vortex persists into the beginning of the next swim cycle maximum vorticity values of 11 s⁻¹ (s.d. 3) are observed. Vorticity in this same region for animals starting from rest was near zero (0.2 s⁻¹ s.d. 0.1).

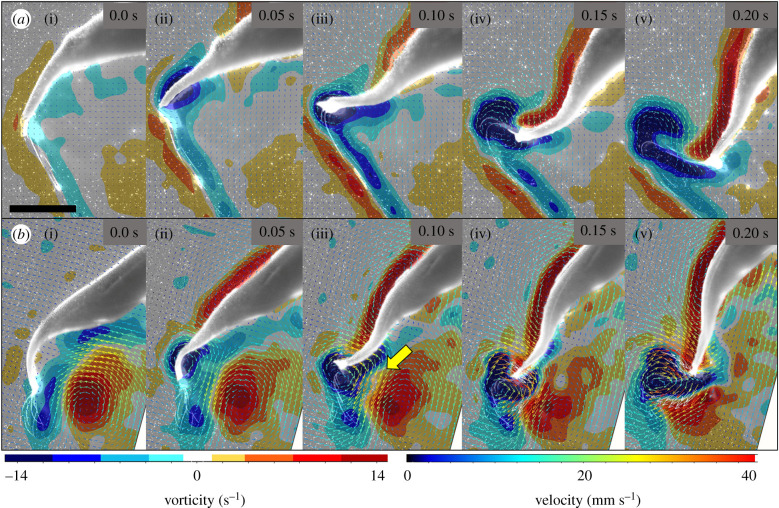
As a swim cycle is initiated, a vortex ring termed a starting vortex forms at the tip of the bell margin (figures 2 and 3) and has an opposite sign to the stopping vortex. In steady swimming cases, the bell margin and resulting starting vortex are forced towards and begin to interact with the opposite sign stopping vortex. This creates a zone of convergent flow directly underneath the bell margin (figure 3). After the contraction phase, the jellyfish's bell resets during the relaxation phase of the swim cycle. The upward and outward movement of the bell margin both enhances the strength of the stopping vortex and keeps it positioned close to the subumbrellar surface [22]. The rotation of the stopping vortex as it sits under the animal drives fluid against the subumbrellar surface which contributes to the passive energy recapture effect [16]. In A. aurita, the next contraction cycle begins before the stopping vortex dissipates (figures 2 and 3). This overlap in space and time of the starting and stopping vortices results in the two vortices interacting at the ventral side of the propulsor. Fluid is driven towards the subumbrellar surface from the stopping vortex and away from the subumbrellar surface by the movement of the bell margin itself (figures 3, 5b).

Figure 3.

Fluid vorticity and velocity vectors around the bell margin for a representative jellyfish swimming sequence when the animal begins from rest (a) and when undergoing steady swimming (b). Yellow arrow indicates region of highest flow due to vortex interface acceleration (VIA). This only occurs when a stopping vortex is present under the animal.

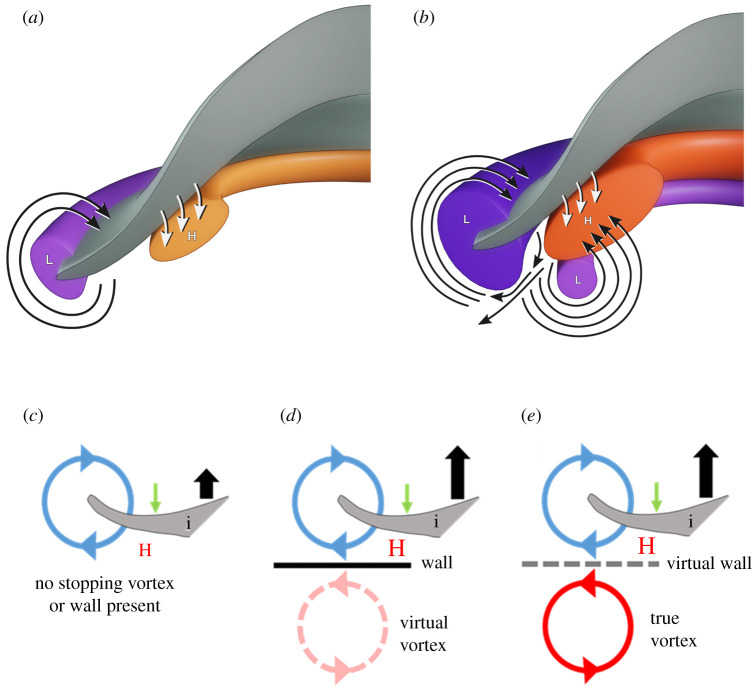
Figure 5.

Diagrammatic representations of water movement and pressure anomalies due to kinematic movement of the jellyfish bell. Note: a cross section through only one half of the animal is depicted (grey surface) for simplicity. (a) Jellyfish swimming without a developed stopping vortex underneath the bell. (b) Jellyfish swimming with a developed stopping vortex underneath the bell. Red areas denote regions of above ambient pressure and blue regions denote regions of below ambient pressure. Darker colours represent higher magnitudes of pressure. Blue lines show the direction of fluid motion. Green arrows show the direction of movement of the bell margin during the contraction phase and black arrows depict the relative forward thrust generated. (c) Away from any solid boundary and without the presence of an additional opposite sign vortex. (d) Ground effect case where swimming near a solid boundary produces an opposite sign virtual vortex and results in greater positive pressures compared to (a). Adapted from [8]. (e) Away from a solid boundary with a real opposite sign stopping vortex present. This case represents a jellyfish undergoing routine swimming and results in a ‘virtual ground effect’ thrust benefit similar to (b). Jellyfish bell margin represented by symbol (i). Green arrows denote direction of propulsor motion and black arrows denote relative thrust generation. Size of the letter ‘H’ denotes the relative strength of high pressure. (Online version in colour.)

While the starting vortex is always present during A. aurita swimming, the strength in terms of vorticity of the starting vortices was significantly lower (T-test, p = 0.02, n = 8) for animals starting from rest. This is despite having the same bell kinematics as steady swimmers with peak vorticity values of 18 s⁻¹ (s.d. 3) and 25 s⁻¹ (s.d. 5), respectively (figure 2). The stronger starting vortices in steady swimmers coincide with the presence of opposite sign stopping vortices that were formed during the previous swimming cycle (figure 2).

The highest fluid speeds were observed at the interface of these opposite sign vortices, at the subumbrellar surface of the bell (figure 3) and particle tracking showed that at least some of the moving fluid that was accelerated between starting and stopping vortices ended up entrained into the growing starting vortex during the contraction of the jellyfish bell. For cases where no stopping vortices were present prior to bell contraction, the highest fluid velocities were observed on the aboral side of the bell margin (figure 3a) and the strong convergent flows at the subumbrellar surface were not observed.

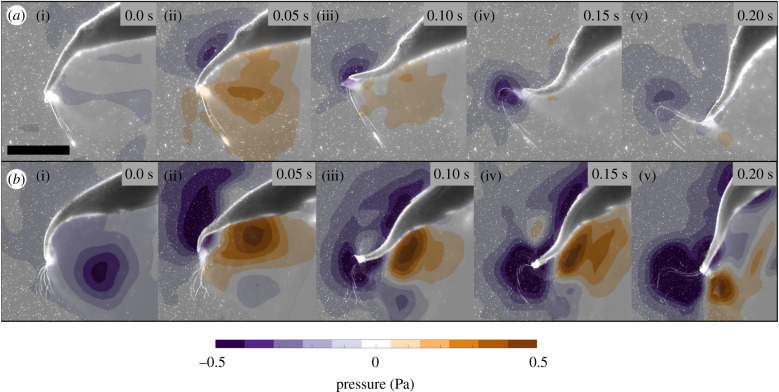
In order to determine the role that vortex–vortex interactions plays in jellyfish swimming, we calculated the pressure fields around the bell margin of swimming medusae. In cases where the stopping vortex was absent, pressure fields near the bell margin were near ambient just prior to contraction (figure 4). Conversely, swimming cases where the stopping vortex was present prior to bell contraction saw a region of negative pressure at the location of the stopping vortex (figure 4). The mean peak negative pressure in this region just prior to bell contraction was −0.35 Pa (n = 5, s.d. 0.17). Within 100 ms after bell contraction is initiated, a strong positive pressure region appeared at the subumbrellar surface of the bell margin (figure 4). Peak positive pressures in this region reached 0.74 Pa (n = 5, s.d. 0.08). These positive pressures were significantly stronger (T-test, p < 0.001, n = 5) when a stopping vortex was present compared to swim cycles without a stopping vortex (0.32 Pa, n = 5, s.d. 0.09). The peak instantaneous force generated at the subumbrellar surface of the bell margin due to positive pressure was approximately 2 × 10⁻⁴ N. This was 2.7 times greater than occurred without the presence of a stopping vortex (0.75 × 10⁻⁴ N). Peak negative pressures around the bell margin of −0.34 Pa (n = 5, s.d. 0.11) were observed when no stopping vortex was present and reached a peak value of −0.51 Pa (n = 5, s.d. 0.12) when a stopping vortex was present. However, peak negative pressures were not significantly different (t-test, p = 0.120, n = 5).

Figure 4.

Pressure fields calculated from the same jellyfish swimming sequences as in figure 3 when the animal begins from rest (a) and when undergoing steady swimming (b). Scale bar = 0.5 cm.

4. Discussion

Compared to more derived taxa such as fish, where swimming kinematics differ greatly between starting from rest and when steadily swimming [28–30], medusae display a very limited range of motion (figure 2). This is due to the fact that the inner nerve ring network of neurons produce all-or-none overshooting action potentials that precede each swimming contraction [31], thereby limiting the range of kinematic variation during swimming. The generation of consistent swimming kinematics whether starting from rest or already undergoing steady swimming provides a unique opportunity to explore the role of vortex interactions in biological propulsion.

The similarities between performance enhancement in jellyfish when vortex–vortex interactions occur and that of near-wall swimmers is striking considering jellyfish are achieving these benefits well away from any solid surface. This can be resolved by the fact that the ground effect is realized with a simple symmetry approach by computing the flow around the object and its virtual mirror image, considering the symmetry-line as the ground [8]. In the case of jellyfish, the animals simply appear to be substituting the mirrored virtual vortex with a real one, thus making the ground or wall virtual instead (figure 5). We thus describe the jellyfish circumstance as a ‘virtual wall’ effect. Engineers frequently consider ways to employ ground effect [32,33] because it can greatly improve the thrust and efficiency of a propulsor; however, the requirement of propelling very near a solid boundary limits potential applications. The ability to arrange vortices to create a ‘virtual wall’ as in jellyfish swimming demonstrates a currently unrecognized potential for future engineered vehicles to benefit from a ground effect without actually requiring the ground.

A mechanistic explanation of this phenomenon must consider that the magnitude of the pressure gradient on either side of a propulsor is directly related to the thrust generated [34–36]. The convergence of fluid at the vortex interface results in significantly stronger positive pressure fields along the subumbrellar surface of the bell margin (figure 3) and provides medusae with additional thrust without the need to alter swimming kinematics. Negative pressures were greater but not significantly different in cases where a stopping vortex was present (table 1). Peak negative pressure values always occurred on the aboral side of the bell margin where the starting vortex was forming. The link between greater vorticity/negative pressures and the presence of a stopping vortex is not as direct as the elevated positive pressure observations but may be due to the interaction of the starting and stopping vortices during bell contraction. The highest fluid velocities during the bell contraction occur in a jet formed at the interface of the stopping and starting vortices (figure 2). By contrast, when no stopping vortex is present, the highest fluid velocities occur at on the dorsal side of the bell margin. It is interesting to note that our observations of swimming speed enhancement of 41% when a vortex–vortex interaction occurs near the propulsor tip of jellyfish is nearly identical to the maximum 40% thrust enhancement observed during ground effect experiments of a pitching foil near a solid wall [13]. Estimating the energetic gain from the ‘virtual wall’ effect, however, is challenging. While the cost of transport for a steady swimming Aurelia is known, the case where the stopping vortex is absent only occurs when the animal has paused and starts swimming again from rest. Thus, the behaviour does not occur on a continual enough basis to extract reliable oxygen consumption estimates. However, when considering that kinematics, and thus muscle energetic expenditure, is roughly the same in both cases yet speed differs greatly, we can reliably speculate that the cost of transport would rise without the presence of a stopping vortex (virtual wall effect).

The origin of the interaction between starting and stopping vortices begins as the medusa contracts its bell, forcing the growing starting vortex closer and closer to the existing stopping vortex (figure 3). This causes a strong jet to form at the interface and quickly reduces the magnitude of the stopping vortex as rotational energy is translated into the straight jet (figure 3). This straight jet is known as the vortex interface acceleration (VIA) [37] and its formation appears to coincide with thrust in several types of swimmers [36,37]. At the interface of the starting and stopping vortices rotational momentum is converted to a straight jet momentum and accelerates the overall flow adjacent to the bell margin. Through particle tracking, we observed that some of the fluid from this high-velocity jet is incorporated into the starting vortex as bell contraction progresses. Thus, by incorporating this high-speed fluid into the starting vortex, it appears that medusae can also generate stronger vortices and greater negative pressures without significantly altering the bell margin kinematics and presumably energetics. This may also have implications for feeding as the starting vortex as well as the induced jet from the VIA interact directly with the tentacles along the margin of the jellyfish bell (figure 3). Thus, enhanced flows near the tentacles can increase volume flux which could promote greater encounter rates with prey.

The development of jellyfish as a model to understand effective propulsion through a fluid has many potential benefits. Unlike other swimmers such as crustaceans, cephalopods and fish, jellyfish are constrained by having muscle tissue that is only a single-cell mono-layer thick [18]. This limits the power that medusae can create when swimming. However, given this resource limitation of power output available for propulsion, there could have been enhanced selective pressure [38] in this group of animals to develop and refine mechanisms to organize fluid and vortices for maximal performance. Medusae can serve as a model for understanding swimming in other taxa as well. For example, fish have many control surfaces (i.e. median fins) that independently and simultaneously generate vortices as they swim. Thus, knowing how medusae use multiple vortices may be advantageous when investigating vortex interactions in other taxa such as between a fish's median fins and tail. It is currently unknown how widespread vortex–vortex interactions with animal propulsive structures are in nature, as we are aware of very few other examples [39]. However, given observations of wake capture in insects [40] and the substantial interest in developing bioinspired vehicles, especially those based on a jellyfish platform [41–43], this represents an important direction for future investigation. For instance, underwater vehicle efficiency in open water could be improved if vortices that are shed in the wake are first directed in a way so as to interact and enhance pressure gradients along a propulsive surface.

Data accessibility

The datasets/videos generated during and/or analysed during the study are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.djh9w0vzf [44].

Authors' contributions

B.J.G., S.P.C. and J.H.C. designed the experiments. B.J.G. collected the data. B.J.G., K.T.D. and K.R.S. analysed the data. B.J.G. wrote the initial draft of the manuscript and all authors contributed to revising the manuscript.

Competing interests

Authors declare no competing interests.

Funding

This research was supported by grants from the National Science Foundation (CBET-1511996 and OCE-1829945) to B.J.G. and (OCE-1536688 and OCE-1829913) to S.P.C. and J.H.C.