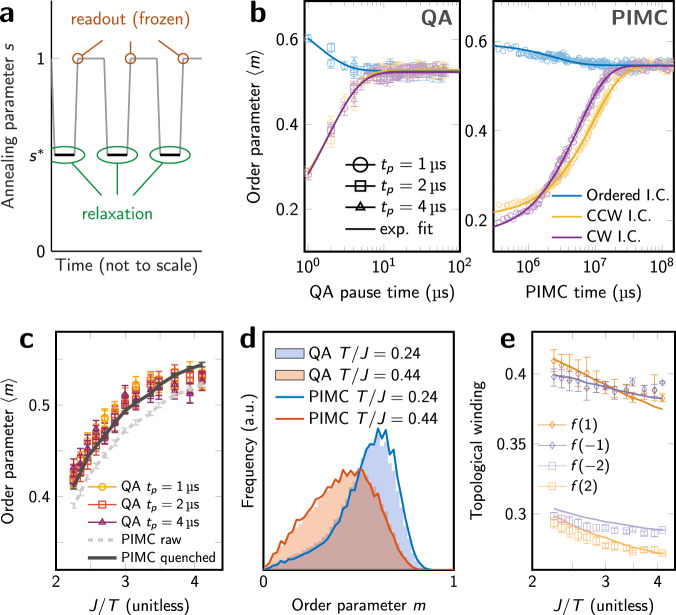
Fig. 2. Convergence of statistical estimates for 1440-spin lattice.

a The QA protocol alternates between equilibration and readout, forming a chain of annealing cycles, each containing a pause of length t_p during which relaxation occurs in the simulated model, parameterized by s^* (Supplementary Information). This breaks the simulation into discrete units, allowing observation of QA equilibration as in the Markov-chain PIMC simulation. b Starting from ordered, CCW, and CW initial conditions (Fig. 1), time-dependent QA and PIMC estimates of the order parameter $⟨m\left(t\right)⟩$ converge to terminal values $⟨m⟩$ for parameters Γ/J = 0.736 and T/J = 0.244. Fit lines show exponential convergence to equilibrium from each initial conditions. c QA estimates of $⟨m⟩$ closely agree with quenched PIMC results (with local excitations removed) over a range of temperatures for Γ/J = 0.736, for two mappings of the lattice onto the QA processor. We attribute the underestimate of 0.01 at low temperatures to disorder in the Hamiltonian (Supplementary Information). d Histograms of m at high and low temperatures for Γ/J = 0.736 show accurate simulation of the entire distribution. e Topological winding from higher-order Fourier weights (Supplementary Information) shows that QA accurately simulates a subtle temperature-dependent preference between CCW (positive) and CW (negative) winding (lines = PIMC, symbols = QA). All error bars are 95% confidence interval on the mean.