HiC-ACT: improved detection of chromatin interactions from Hi-C data via aggregated Cauchy test

Summary

Genome-wide chromatin conformation capture technologies such as Hi-C are commonly employed to study chromatin spatial organization. In particular, to identify statistically significant long-range chromatin interactions from Hi-C data, most existing methods such as Fit-Hi-C/FitHiC2 and HiCCUPS assume that all chromatin interactions are statistically independent. Such an independence assumption is reasonable at low resolution (e.g., 40 kb bin) but is invalid at high resolution (e.g., 5 or 10 kb bins) because spatial dependency of neighboring chromatin interactions is non-negligible at high resolution. Our previous hidden Markov random field-based methods accommodate spatial dependency but are computationally intensive. It is urgent to develop approaches that can model spatial dependence in a computationally efficient and scalable manner. Here, we develop HiC-ACT, an aggregated Cauchy test (ACT)-based approach, to improve the detection of chromatin interactions by post-processing results from methods assuming independence. To benchmark the performance of HiC-ACT, we re-analyzed deeply sequenced Hi-C data from a human lymphoblastoid cell line, GM12878, and mouse embryonic stem cells (mESCs). Our results demonstrate advantages of HiC-ACT in improving sensitivity with controlled type I error. By leveraging information from neighboring chromatin interactions, HiC-ACT enhances the power to detect interactions with lower signal-to-noise ratio and similar (if not stronger) epigenetic signatures that suggest regulatory roles. We further demonstrate that HiC-ACT peaks show higher overlap with known enhancers than Fit-Hi-C/FitHiC2 peaks in both GM12878 and mESCs. HiC-ACT, effectively a summary statistics-based approach, is computationally efficient (∼6 min and ∼2 GB memory to process 25,000 pairwise interactions).

Introduction

Chromatin spatial organization plays a critical role in genome functions such as transcription regulation and DNA replication.1, 2, 3 Studies have shown that millions of putative cis-regulatory elements, such as enhancers, exist within the genome; many of these elements are far away in one-dimensional (1D) genomic distance from their target genes (e.g., up to 1 Mb away).^1,2,4, 5, 6 Because of the abundance of enhancers and their long-range regulation roles, systematic mapping of enhancer-promoter interactions is challenging.¹

Genome-wide chromosome conformation capture techniques such as Hi-C⁷ have been widely used to study three-dimensional (3D) organization of chromatin. Hi-C data can be summarized into a contact matrix of all possible pairwise interactions between ligated fragments genome wide. As comprehensive chromatin interaction maps become increasingly prominent as a result of increases in sequencing capacity and decreases in cost, there is an urgent need to develop tools to analyze and interpret this type of data.⁸ Such methods to detect statistically significant long-range chromatin interactions (also referred to as “peak callers”) seek to determine whether the observed contact frequency is significantly higher than expected from chromatin random collision.

Fit-Hi-C⁹ is a popular method to evaluate pairs of chromatin loci independently, and it assigns each pair a statistical confidence (p value). Fit-Hi-C corrects distance dependence and potential systematic biases in Hi-C datasets by fitting non-parametric splines to model the background chromatin contact frequency.9, 10, 11 Recently, a re-implementation, FitHiC2,¹⁰ was released. Along with the addition of new computational modules, FitHiC2 can be applied to the highest-resolution Hi-C datasets currently available.¹⁰ However, in high-resolution data (e.g., 5 or 10 kb bin resolution), neighboring chromatin interactions are unlikely to be independent, as assumed in FitHiC2. When this independence assumption is violated, the p values corresponding to chromatin interactions are inaccurate.

We have previously demonstrated that spatial dependency is non-negligible when analyzing Hi-C data at high resolution. Accordingly, we developed hidden Markov random field (HMRF)-based methods, HMRF-Bayes¹² and FastHiC,¹³ to accommodate spatial dependency for improved statistical properties. However, compared with FitHiC2, which analyzes each pair of chromatin loci separately, our HMRF-based framework is more computationally intensive.

HiCCUPS¹⁴ (Hi-C computational unbiased peak search) is another commonly adopted method for identifying significant chromatin interactions. Unlike Fit-Hi-C/FitHiC2 and our HMRF-based methods, which use a global background model,^9,10,12 HiCCUPS uses a local background model where each chromatin loci pair has a unique model influenced by information from local neighborhoods.¹⁴ This model defines peaks on the basis of whether the loci pair interacts significantly more frequently than loci pairs in its neighborhood. Therefore, HiCCUPS effectively detects summits of chromatin interactions rather than peaks identified in Fit-Hi-C/FitHiC2 and our HMRF-based methods. A most recently published method, MUSTACHE, similarly relies on a local background model and detects summits by using a scale-space modeling framework enlightened by methods in computer vision.¹⁵ The summit-detection strategy is valuable in distinguishing the most frequently interacting pairs from its neighborhood but limits its ability to identify many functionally important interactions linking cis-regulatory elements such as promoters and enhancers.^10,14

In this paper, we develop HiC-ACT, a method for post-processing peak calling results from methods that do not consider spatial dependency. HiC-ACT’s post-processing via an aggregated Cauchy test approach accounts for possible correlation between adjacent loci pairs from high resolution Hi-C data. HiC-ACT, a summary statistics-based approach, is flexible in application, only requiring the input of bin identifiers and corresponding raw p values generated from established 3D peak callers rather than raw Hi-C data. HiC-ACT also allows users to specify a smoothing parameter based on the data resolution. Moreover, HiC-ACT does not require any information about the underlying correlation structure in the data while being able to account for the inherent correlation between bin (loci) pairs.

The implementation of p value smoothing in HiC-ACT improves identification of significant chromatin interactions and recovers information lost in sparse data. Since HiC-ACT borrows information from neighboring loci pairs, it calls peaks rather than summits. Thus, we chose to compare HiC-ACT to FitHiC2. Both simulation studies and real data analysis demonstrate that HiC-ACT outperforms FitHiC2 in increasing recall with comparable precision.

In the remainder of this article, we specify the HiC-ACT model and provide details regarding the workflow. Next, we show real data-based simulation results based on Hi-C data from the human lymphoblastoid cell line GM12878 at various sequencing depths. Then, we perform real data analysis using Hi-C datasets from GM12878 and mouse embryonic stem cells (mESCs). Finally, we conclude with some discussions.

Material and methods

Aggregated Cauchy combination test

HiC-ACT is based on the aggregated Cauchy combination test¹⁶ to combine a set of p values, ${\text{p}}_1,{\text{p}}_2,\dots ,{\text{p}}_{\text{k}}$. We use a linear combination of transformed p values with non-negative weights:

$$\begin{array}{l}T=\sum _{i=1}^k{w}_i\tan \left\{\left(0.5-{\text{p}}_i\right)\pi \right\},\hfill \end{array}$$ (Equation1)

where ${\text{p}}_i$ is the individual p value, $w_i$ is the non-negative weight such that $\sum _{i=1}^k{w}_i=1$, and k is the total number of p values to be combined. When only one p value is considered $\left(k=1\right)$, it is straightforward to show that $T$ follows a Cauchy distribution (location parameter$x_0=0$, scale parameter $\gamma =w_1=1$) under the null hypothesis that ${\text{p}}_1$ is uniformly distributed between 0 and 1.¹⁶ Liu and Xie showed that this combination of p values, $T$, follows a standard Cauchy distribution $\left(x_0=0,\gamma =1\right)$under the null hypothesis.¹⁶ Assume that the p values are calculated from Z scores and let $\mathbf{X}={\left(X_1,X_2,\dots ,X_k\right)}^T$, where $X_i$ is a test statistic corresponding to ${\text{p}}_i$. The null hypothesis can then be written as $H_0:\text{E}\left[\mathbf{X}\right]=0$.

Thus, ${\text{p}}_i$ can be expressed as ${\text{p}}_i=2\left(1-\Phi \left(\left|X_i\right|\right)\right)$. We can then rewrite $T$ (Equation 1) as follows:

$$\begin{array}{l}T\left(\mathbf{X}\right)=\sum _{i=1}^k{w}_{i}tan\left\{\left(2\Phi \left(\left|X_i\right|\right)-1.5\right)\pi \right\}.\hfill \end{array}$$ (Equation2)

If the ${\text{p}}_i$s are perfectly dependent (i.e., all the ${\text{p}}_i$s are equal or linear functions of one another) or perfectly independent, it can be shown that the sum of multiple independent Cauchy random variables also follows a Cauchy distribution. Furthermore, it has been shown that this holds even when the ${\text{p}}_i$s are correlated.^16,17

Liu et al. further showed that under arbitrary dependency structures $T\left(\mathbf{X}\right)$ has approximately a Cauchy tail.^16,17 They also demonstrated that when the ${\text{p}}_i$s are correlated, it has very limited effect on the tail of the distribution. Consequently, we can transform the test statistic $T$ back to a p value by using Cauchy(0,1)

$$\begin{array}{l}{\text{p}}_T\approx \frac{1}{2}-\frac{1}{\pi }{\tan }^{-1}\left\{T\right\}.\hfill \end{array}$$ (Equation3)

Because of the heavy tail of the Cauchy distribution, T is insensitive to the correlation of the p values, especially at the tail of the distribution, lending to accurate approximations for small p values.^16,17 This desirable property of this approximation (Equation 3) with small p values is of particular interest in Hi-C data analysis. Liu et al. also argued that if the individual p values are conservative, ${\text{p}}_T$ will be conservative as well and the type I error is controlled.¹⁷

HiC-ACT test statistic

Using the framework above, we specify the HiC-ACT test statistic as follows. Let ${\text{p}}_{ij}$ represent the p value for chromatin interaction between bin $i$ and bin $j$ from a specific Hi-C peak calling method. Consider the null hypothesis that the contact frequency between bin pair $\left(i,j\right)$ is due to random chromatin collision. Define the HiC-ACT test statistic $T_{AC{T}_{ij}}$ as

$$\begin{array}{l}{T}_{AC{T}_{ij}}=\sum _{0\le \left|m-i\right|+\left|n-j\right|\le h}{w}_{mn}tan\left\{\left(0.5-{\text{p}}_{mn}\right)\pi \right\}.\hfill \end{array}$$ (Equation4)

Here, $h$ is the local smoothing bandwidth. We followed the strategy adopted by the HiCRep¹⁸ method to determine the size of the smoothing window based on data resolution (Table S1). We take $w_{mn}$ to be the Gaussian kernel weight function, defined as

$$\begin{array}{l}{w}_{mn}=\frac{\exp \left\{\frac{-d_{mn}^2}{2}\right\}}{{\sum }_{0\le \left|m^{\text{′}}-i\right|+\left|n^{\text{′}}-j\right|\le h}\exp \left\{\frac{d_{m^{\text{′}}{n}^{\text{′}}}^2}{2}\right\}}st\sum w_{mn}=1,\hfill \end{array}$$ (Equation5)

$$where{d}_{mn}^2={\left(m-i\right)}^2+{\left(n-j\right)}^2.$$

The criterion in Equation 4 that determines which bin pairs are included in the chromatin interaction neighborhood is derived from the equation of a diamond and ensures that the p values of all bin pairs $\left(m,n\right)$ within a specified distance $\left(h\right)$ from the bin pair of interest $\left(i,j\right)$ are combined. Note that the p value for the bin pair itself contributes to the statistic and, thus, the smoothed p value.

On the basis of the theory established, $T_{AC{T}_{ij}}$ approximately follows a standard Cauchy distribution under the null hypothesis. Therefore, the p value for $T_{AC{T}_{ij}}$ can be approximated by

$$\begin{array}{l}{\text{p}}_{ij}^{\text{∗}}\approx 0.5-\frac{\left({\tan }^{-1}\left\{T_{AC{T}_{ij}}\right\}\right)}{\pi }.\hfill \end{array}$$ (Equation6)

We can interpret ${\text{p}}_{ij}^{\ast }$ as the local neighborhood smoothed p value. Intuitively, for a biologically meaningful chromatin interaction, all bin pairs in its neighborhood are more likely to have significant p values. Thus, the combined p value ${\text{p}}_{ij}^{\ast }$ tends to be more significant and is driven by small p values in its neighborhood.

In an application to rare variant association analysis, Liu et al. demonstrated that the aggregated Cauchy test is powerful under sparse alternatives.¹⁷ Our application to Hi-C data is also subject to sparse alternatives because there are relatively few interactions due to chromatin looping compared to the vast number of random events of chromatin collision. As shown by Liu and Xie, the Cauchy combination test handles arbitrary dependency structures without knowledge of the correlation values.¹⁶ Through this property, HiC-ACT specifically accounts for the inherent correlation across neighboring pairs while maintaining the benefit of not needing to specify the correlations.

Workflow

To implement HiC-ACT, we first obtain results from a standard peak caller not considering spatial dependency. HiC-ACT only requires bin pair identifiers and the corresponding p values. Next, we set $h$ based on the data resolution (see Table S1 for suggestions). Then, we identify a set of bin pairs $\left(i,j\right)$ of interest, e.g., by selecting if ${\text{p}}_{ij}$ is less than a specified threshold. We recommend that this threshold depends on the total number of mapped reads in the data (Table S2). For each $\left(i,j\right)$ pair, HiC-ACT determines all possible $\left(m,n\right)$ pairs that meet criterion in Equation 4, calculates the weights, and then computes $T_{AC{T}_{ij}}$ and its corresponding p value ${\text{p}}_{ij}^{\ast }$ for each $\left(i,j\right)$ pair in the set of interest by using Equation 6.

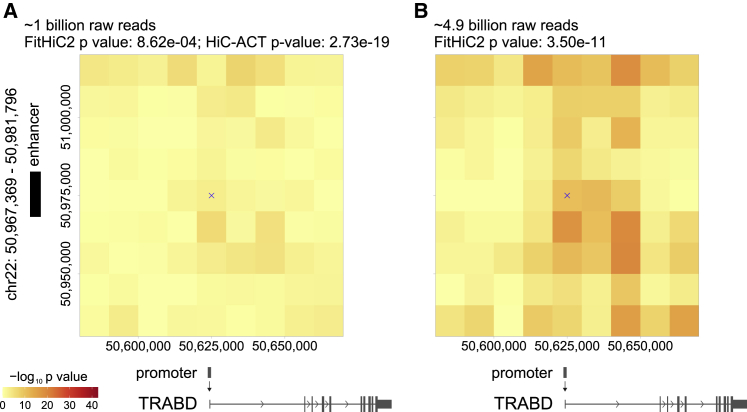
In Figure 1, we present a motivating example for HiC-ACT by using 10 kb GM12878 Hi-C data acquired from the Rao et al. study consisting of ∼4.9 billion pairwise contacts.¹⁴ Each colored pixel on the heatmap represents the strength of the FitHiC2-identified interaction (p value), represented on the −log10 scale. This specific chromatin interaction (i.e., bin pair) is centered at 50,625,000 bp and 50,975,000 bp on chromosome 22 (marked by a blue “x”) and has one end overlapping with a super-enhancer reported by the Roadmap Epigenomics Consortium¹⁹ and the other end overlapping with the transcription start site (TSS)²⁰ of the highly expressed TRABD gene (FPKM = 17).²¹ However, when the data is down-sampled to ∼1 billion raw reads (a more realistic sequencing depth), this interaction is not classified as a significant peak by FitHiC2 (p = 8.62e−4) (see Table S2 for details on how peaks were determined) (Figure 1A). When HiC-ACT is applied to these FitHiC2 results, the resulting p value is highly significant (p = 2.73e−19) as expected given the biological evidence. Figure 1B displays the corresponding heatmap for FitHiC2 interactions/p values called on the full GM12878 data (∼4.9 billion reads). The FitHiC2 p value here for the specified interaction is 3.50e−11. Comparing Figure 1A to Figure 1B, we notice that information is lost in data with shallower sequencing depth. HiC-ACT is able to recover some information lost in Hi-C data with shallower sequencing depths by leveraging information from neighboring loci.

Figure 1.

Motivating example for HiC-ACT

(A and B) FitHiC2 was applied to the GM12878 10 kb Hi-C data down-sampled to ∼1 billion raw reads (A) as well as to the full GM12878 data (∼4.9 billion raw reads) (B). Each colored pixel on the heatmap represents the strength of the FitHiC2 interaction (p value), represented on the −log10 scale. Here, the chromatin interaction (i.e., bin pair) of interest is centered at 50,625,000 bp and 50,975,000 bp on chromosome 22 (marked by a blue “x”). This interaction has one end overlapping with an identified super-enhancer from the Roadmap Epigenomics Consortium (marked by black bar on the left side) and the other end overlapping with the transcription start site (TSS) for TRABD, indicating a possible functional interaction. However, this interaction is not marked as significant by FitHiC2 in the lower sequencing depth (p = 8.62e−4) (A). When HiC-ACT is applied to these FitHiC2 calls, the resulting p value is highly significant (p = 2.73e−19) as expected given the biological evidence. By using information from neighboring loci, HiC-ACT is able to recover some information lost in Hi-C data with shallower sequencing depth.

We also note that there are other bin pairs in this illustrated neighborhood with significant interactions. As mentioned previously, HiC-ACT and FitHiC2 call peaks rather than summits. Calling peaks ensures a higher coverage of capturing functional chromatin interactions, as opposed to calling summits, which can be driven by a combination of stochasticity and proximity to bona fide interactions. Although the highlighted bin pair in Figure 1 does not have the strongest signal, it completely overlaps the enhancer region, as opposed to, for example, the bin pair directly below that only partially overlaps with the enhancer region.

Results

Real data-based simulations

We first used real data-based simulations to assess the performance of HiC-ACT. The simulations were based on the 10 kb GM12878 Hi-C data consisting of ∼4.9 billion pairwise contacts.¹⁴ FitHiC2 results generated from this high-depth data were treated as the truth. Approximately 1.57 million significant chromatin interactions were identified on the basis of the criterion that the observed contact count > 15, the expected contact count > 5, the ratio of observed to expected > 1.5, and the p value < 1.0e−12. The p value threshold was informed by a recent study of 10 kb bin resolution deeply sequenced Hi-C data from human brain cortex, where high-confidence regulatory chromatin interactions were determined with p value < 2.31e−11.⁵

To simulate more realistic sequencing depths and reflect the sequencing depths of most studies, we down-sampled the GM12878 Hi-C data to 10%–40% of the original depth corresponding to ∼0.5–2.0 billion raw reads. We performed down-sampling by generating multinomially distributed random number vectors. The parameters for the multinomial distribution were specified with the down-sampling ratio (i.e., 10%–40%) and the contact counts for bin pairs in the full data. For each of these down-sampled data, we ran FitHiC2 then applied HiC-ACT. Following HiCRep,¹⁸ we chose the smoothing bandwidth (h) to be 20 because we analyzed the data at 10 kb resolution.

Significant pairwise interactions were defined via sequencing depth-specific threshold of minimum observed contact count, minimum expected contact count, global significant p value threshold, and for HiC-ACT, initial p value filtering. In each case, a minimum ratio between observed count and expected count of 1.5 was required to determine a significant interaction. Table S2 provides recommendations for defining significant interactions (i.e., peaks) on the basis of this simulation via sequencing depth-specific initial p value filtering.

Assuming that deeply sequenced data is more reliable than data with shallower sequencing depth, we use the FitHiC2 peak calls (i.e., defined significant interactions) from the full GM12878 data as the working truth in our simulations. Accordingly, we counted the number of interactions correctly classified as significant or insignificant by HiC-ACT and FitHiC2 in each down-sampled data. HiC-ACT correctly identified 75%–641% more significant interactions than FitHiC2 and achieves comparable precision (Table 1 and Table S3).

Table 1.

HiC-ACT considerably improves sensitivity with affordable loss of precision

Sequencing depth (billions)	Sensitivity/recall		Precision		F1 score
	HiC-ACT	FitHiC2	HiC-ACT	FitHiC2	HiC-ACT	FitHiC2
0.5	0.44	0.06	0.92	1.00	0.59	0.11
1.0	0.57	0.16	0.93	1.00	0.71	0.28
1.5	0.65	0.28	0.93	1.00	0.77	0.44
2.0	0.70	0.40	0.93	1.00	0.80	0.57

Sensitivity, precision, and corresponding F1 score (harmonic mean of precision and recall) of calling true peaks at various GM12878 10 kb sequencing depths (in approximate billions of raw reads) is reported. Peaks are defined with the guidelines in Table S2, and peaks called by FitHiC2 in the full GM12878 data (∼4.9 billion raw reads) are treated as working truth.

Although HiC-ACT tends to be driven by the most significant interactions in a neighborhood (those pairs with extremely small p values), it maintains large (i.e., non-significant) p values for truly insignificant interactions. To demonstrate this, we calculated the sensitivity/recall and precision for correct identification of significant interactions for each method. Sensitivity, also known as the true positive rate, is the proportion of true peaks identified out of the total number of true peaks. Precision, also known as the positive predictive value, is the proportion of true peaks identified out of the number of interactions called as peaks. We also report the F1 score, defined as the harmonic mean of precision and recall, where a value of 1 indicates perfect precision and recall. Table 1 displays a summary of these results at various sequencing depths (in billions of raw reads). HiC-ACT considerably improves sensitivity with affordable loss of precision, as demonstrated by greater F1 scores, in all sequencing depths, although the largest improvements are seen when sequencing depth is low. We note that the pattern of these results holds when the global significance threshold is adjusted (Table S3).

In the Hi-C peak calling problem, the number of true positives (significant interactions/peaks) and true negatives (insignificant interactions/background noise) is highly unbalanced. Because of the large proportion of true negatives, comparing sensitivity versus specificity is not ideal. Precision versus recall is a more appropriate performance metric in this scenario.²² Accordingly, specificity is omitted from Table 1 since the values for both methods are nearly 1 because of the large number of insignificant interactions. Specificity, along with peak classification counts, can be found in Table S3.

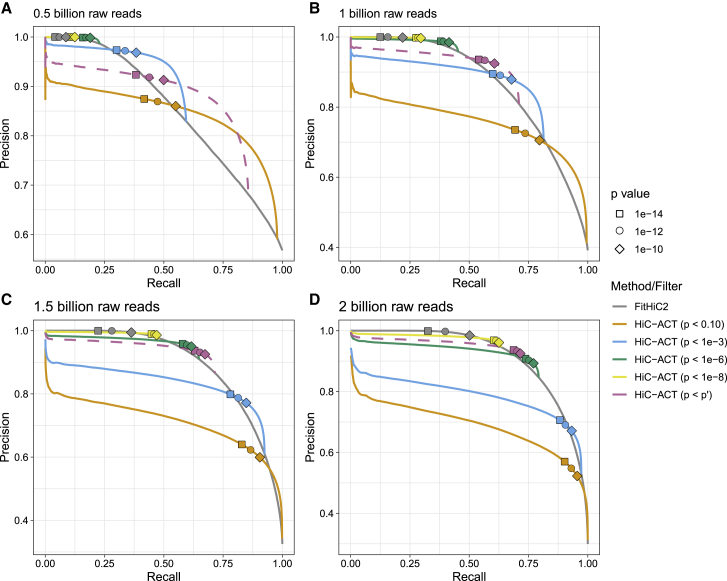
We can further examine the relationship between true positives (i.e., correctly identifying significant interactions/calling true peaks) and false positives (i.e., incorrectly identifying interactions as significant/calling false peaks) through precision-recall curves (PRCs). Ideally, we desire a method that has both high precision (few false positives) and high recall (few false negatives), which is represented by a PRC located in the top right region of the plot. Figure 2 shows the PRCs for calling true peaks (as defined in Table S2) in the GM12878 10 kb data when the data is down-sampled to different depths. Each panel displays the PRC for peaks called via FitHiC2 as well as HiC-ACT. The shapes indicate where a specific p value threshold for defining FitHiC2/HiC-ACT peaks lies on the curve. For example, with ∼0.5 billion raw reads, FitHiC2 (gray curve) achieves a recall of approximately 0.06 and precision near 1 when the significance threshold p is between 1.0e−14 and 1.0e−10. However, HiC-ACT with initial p value filtering of 1.0e−3 (blue curve) is able to significantly improve peak classification, achieving recall of approximately 0.36 with negligible loss in precision (0.97) (Figure 2A).

Figure 2.

Precision-recall curves for calling true peaks

(A–D) Results for the GM12878 10 kb data down-sampled to ∼0.5 billion raw reads (A), ∼1.0 billion raw reads (B), ∼1.5 billion raw reads (C), and ∼2 billion raw reads (D) are shown with a global p value of 1.0e−12 for defining true peaks (using the full ∼4.9 billion raw read data as truth). Each panel displays the precision-recall curve (PRC) for peaks called via FitHiC2 [gray] as well as HiC-ACT with various initial filters (p value < 0.10 [orange], p value < 1.0e−3 [blue], p value < 1.0e−6 [green], p value < 1.0e−8 [yellow], p value < p′ [pink]). The pink dashed line indicates HiC-ACT applied with our suggested filter (values of p′ can be found in Table S2). Shapes indicate where a specific p value threshold for defining FitHiC2/HiC-ACT peaks lies on the curve.

The pink dashed curves correspond to HiC-ACT applied with our suggested filter p′ (values of p′ can be found in Table S2). As detailed in Table S2, we suggest using a more stringent initial p value filter for data with high sequencing depth and using a more lenient initial p value filter for data with shallow sequencing depth. As the sequencing depth increases, the choice of initial p value filter has less effect on the precision and recall of HiC-ACT (Figure 2D). In general, HiC-ACT peak calling can be made more conservative (or liberal) by choosing a more stringent (or lenient) initial p value filtering threshold. In other words, HiC-ACT allows us to improve precision at the cost of recall (e.g., detection of true peaks) by selecting a smaller initial p value filter. We obtained similar results when the global significance threshold is adjusted (Figures S1 and S2 and Table S3).

Lastly, the PRCs also suggest that type I errors are largely maintained in that the curves (particularly the parts where the significant thresholds were selected) are rather flat, reflecting no big drop in precision. Given the much larger number of non-peaks compared to peaks, a small increase in type I error could lead to a rather drastic increase in the denominator for precision calculation, which would incur a big drop in precision. Therefore, it is reassuring to observe that the HiC-ACT PRCs remain largely flat.

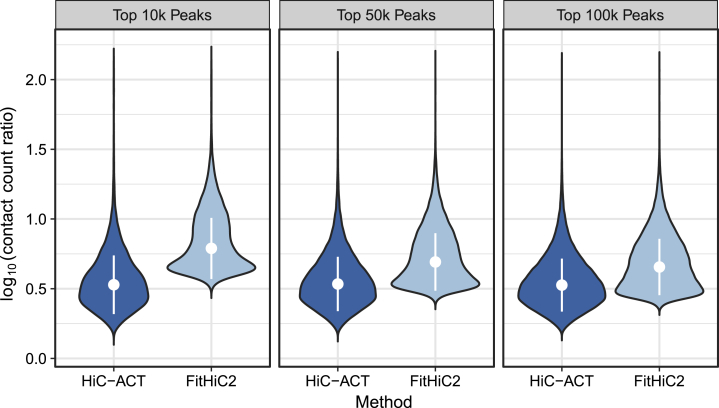
HiC-ACT also shows improved power to detect significant interactions with low normalized contact frequency. Specifically, we compared the observed to expected contact count ratios between methods for their most significant interactions (ranked p values). Figure 3 shows the distribution of the ratios of the most significant true peaks (significant interactions called in the full data) called by each method in the ∼1 billion raw read data. The median ratio for HiC-ACT is ∼3.3 (0.5 on the log10 scale) across all top n peaks, whereas the median ratio for FitHiC2 decreases from 6 to 4.5 (0.8 to 0.7 on the log10 scale) as the number of top peaks increases. The observed to expected contact count ratios of HiC-ACT are significantly lower than those of FitHiC2 (Wilcoxon test p value < 2.2e−16) in each case. We reached similar conclusions at other sequencing depths (0.5–2.0 billion raw reads, data not shown).

Figure 3.

HiC-ACT demonstrates improved power to detect peaks with low normalized counts

Violin plot showing the distribution of the log10 ratio of observed contact counts to expected contact counts for the top true peaks called by HiC-ACT and by FitHiC2 in the GM12878 10 kb data down-sampled to ∼1 billion raw reads. Significant interactions were defined with the criteria specified in Table S2, and the true peaks used here further require that the interaction be identified as significant in the full data. Each violin displays the median ± 1 standard deviation.

HiC-ACT identifies biologically relevant interactions

GM12878 Roadmap Epigenomics Consortium enhancers

Using the same GM12878 Hi-C data at 10 kb bin resolution, we compared the peaks called by HiC-ACT and FitHiC2 to typical enhancers (TEs) and super-enhancers (SEs) reported from the Roadmap Epigenomics Consortium.¹⁹ There are 10,335 enhancers in total, 252 of which are SEs. First, we identified which peaks have one end overlapping with an enhancer and the other end overlapping with the TSS²⁰ of an expressed gene²¹ (FPKM > 1), and defined such peaks as overlapping an enhancer-promoter (E-P) interaction.

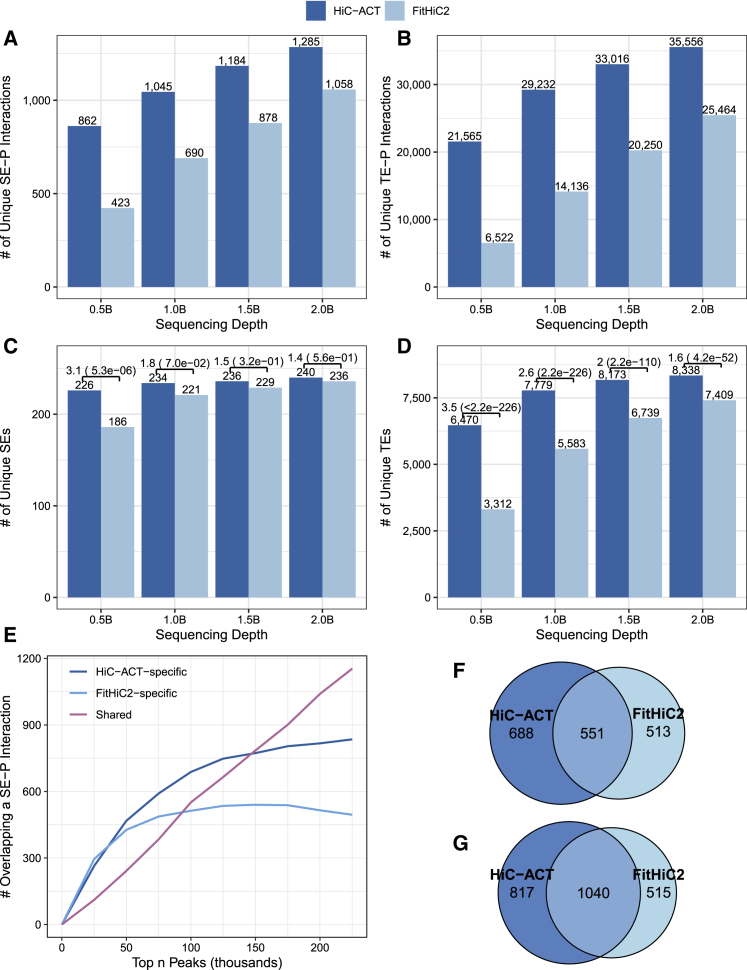
At each sequencing depth, we counted the total number of super-enhancer-promoter (SE-P) interactions (Figure 4A) and typical enhancer-promoter (TE-P) interactions (Figure 4B) identified by each method. HiC-ACT interactions overlap more with SE-P and TE-P interactions compared to FitHiC2 interactions. We also counted the total number of unique SEs (Figure 4C) and unique TEs (Figure 4D) identified by each method. HiC-ACT is able to capture 90%–95% of the SEs and 63%–81% of TEs, compared to 74%–94% and 32%–72%, respectively, captured by FitHiC2. HiC-ACT appears to be less sensitive to sequencing depth than FitHiC2 and shows more significant improvements over FitHiC2 at shallower sequencing depths. Figures 4C and 4D displays the total counts as well as the odds ratios and corresponding p values for the number of enhancers identified (out of 252 total SEs and 10,335 total TEs).

Figure 4.

Comparing HiC-ACT and FitHiC2 peak calls with Roadmap Epigenomics Consortium enhancers in GM12878 10 kb Hi-C data

(A and B) The total number of super-enhancer-promoter (SE-P) interactions (A) or typical enhancer-promoter (TE-P) interactions (B) identified by each method at various sequencing depths (in approximate billions of raw reads).

(C and D) The total number of unique super-enhancers (SEs) (C) or unique typical enhancers (TEs) (D) captured is also reported along with the odds ratios and corresponding p values for number of enhancers identified (out of 252 total SEs and 10,335 total TEs).

(E) The number of HiC-ACT-specific, FitHiC2-specific, and shared interactions overlapping a SE-P interaction within a specified number of top peaks (ranked p values) in the GM12878 data down-sampled to ∼1 billion raw reads, demonstrating that the most significant interactions identified by each method are different.

(F and G) The breakdown of overlap counts for this example is detailed for the top 100,000 peaks (F) and the top 200,000 peaks (G).

Next, we examined the total number of interactions overlapping an E-P interaction within a specified number of top peaks (ranked p values). At all sequencing depths (∼0.5–2.0 billion raw reads), we observed improved performance of HiC-ACT over FitHiC2 for SE-P interactions and comparable performance between HiC-ACT and FitHiC2 for TE-P interactions (Figure S3). Moreover, the most significant interactions identified by each method are different (Figures 4E–4G). Figure 4E illustrates the number of HiC-ACT-specific, FitHiC2-specific, and shared peaks that overlap an SE-P interaction at various top peaks. For example, out of the top 100,000 peaks called by HiC-ACT and FitHiC2, 1,219 and 1,064 peaks overlap with SE-P interactions, respectively. Among them, 688 peaks are HiC-ACT specific, 513 peaks are FitHiC2 specific, and 552 peaks are shared by two methods (Figure 4F). A similar example for the top 200,000 peaks called by each method is displayed in Figure 4G.

mESC ChIP-seq/ATAC-seq peaks

We applied HiC-ACT (h = 20) to FitHiC2 results from Hi-C data from mESCs at 10 kb bin resolution.²³ Because this data is deeply sequenced (∼7 billion reads), we chose a HiC-ACT initial p value filter of 1e−6. This choice was informed by the PRCs in Figure 4D. Significant interactions were defined with the same thresholds as the GM12878 data (observed contact count > 15, expected contact count > 5, the ratio of observed to expected contact counts > 1.5, and global p value < 1.0e−12). By these criteria, HiC-ACT identifies ∼1.8 million significant interactions and FitHiC2 identifies ∼1 million significant interactions.

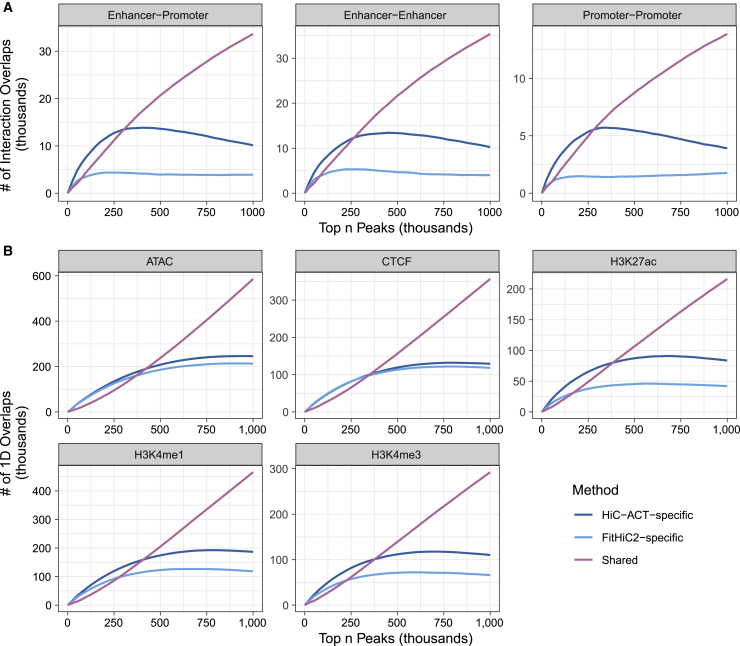
We compared these peak calls to mESC ChIP-seq (H3K4me3, H3K4me1, H3K27ac, and CTCF) peaks24, 25, 26 and ATAC-seq peaks.²⁶ We defined an overlap as a HiC-ACT/FitHiC2-called peak with either 10 kb bin overlapping a ChIP-seq/ATAC-seq peak. Further, we defined a 10 kb bin as an enhancer bin or a promoter bin if it overlaps with a H3K27ac ChIP-seq peak or H3K4me3 ChIP-seq peak and TSS²⁰ of an expressed gene²⁷ (FPKM > 1), respectively. We defined a HiC-ACT- or FitHiC2-identified peak as an E-P interaction if one anchor bin is an enhancer bin and the other anchor bin is a promoter bin. We similarly defined enhancer-enhancer (E-E) and promoter-promoter (P-P) interactions.

Because HiC-ACT identifies more significant interactions than FitHiC2, we examined the same number of top most significant interactions (ranked by p values) called by each method for a fair comparison. The most significant HiC-ACT-specific interactions show higher overlap with E-P, E-E, and P-P interactions than the same number of most significant FitHiC2-specific interactions (Figure 5A). The odds of the most significant HiC-ACT peaks showing overlap with E-P, E-E, or P-P interactions is significantly higher (odds ratio estimate ≈ 1.5, p value < 2.2e−16) than the odds of the most significant FitHiC2 peaks (Table S4). We observed similar results when only considering the 1D overlaps in H3K27ac, H3K4me1, and H3K4me3 ChIP-seq peaks and a comparable performance between HiC-ACT and FitHiC2 in ATAC-seq peaks and CTCF ChIP-seq peaks (Figure 5B). Table S4 lists the number of overlaps displayed by Figure 5 at various numbers of top peaks.

Figure 5.

Comparing HiC-ACT and FitHiC2 peak calls with ChIP-seq and ATAC-seq peaks in mESC data

(A) The number of most significant HiC-ACT and FitHiC2 interactions overlapping with an enhancer mark or promoter mark. The most significant HiC-ACT-specific interactions show higher overlap with enhancer-promoter, enhancer-enhancer, and promoter-promoter interactions than the same number of most significant FitHiC2-specific interactions.

(B) The number of 1D overlaps between a 10 kb bin from most significant HiC-ACT and FitHiC2 interactions and a ChIP-seq/ATAC-seq peak. We see similar results when only considering the 1D overlaps in H3K27ac, H3K4me1, and H3K4me3 ChIP-seq peaks and a comparable performance between HiC-ACT and FitHiC2 in ATAC-seq peaks and CTCF ChIP-seq peaks. See Table S4 for details relevant to this figure.

mESC FANTOM5 and dbSUPER enhancers

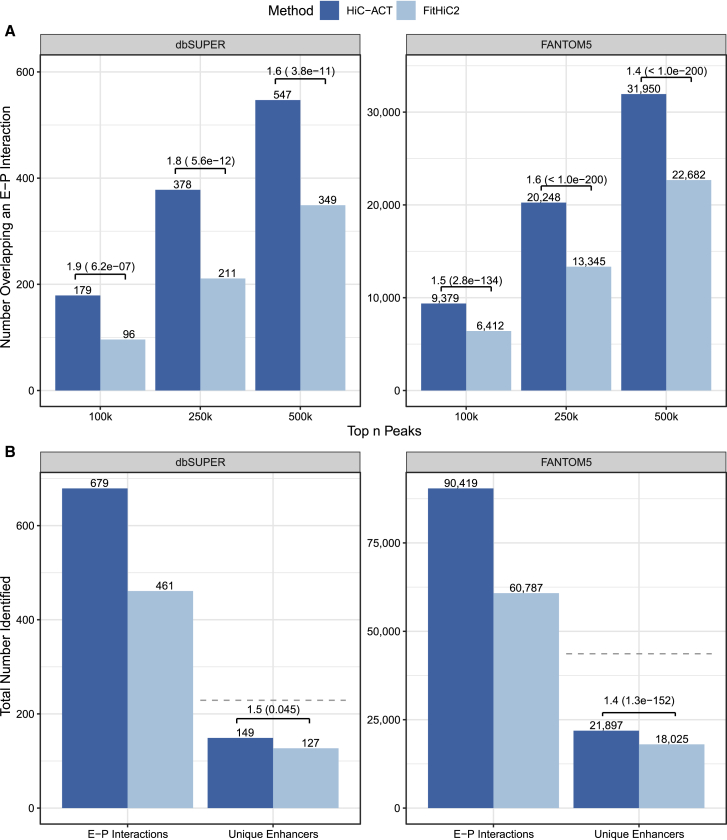
Next, we compared the mESC HiC-ACT and FitHiC2 calls at 10 kb resolution to mESC enhancers cataloged in the FANTOM5^, database^28,29 and from the dbSUPER database.³⁰ FANTOM5 includes 43,662 enhancers and dbSUPER includes 229 SEs. For each set of enhancers, we counted how many interactions called by HiC-ACT and FitHiC2 overlap with an E-P interaction (one end overlapping with an enhancer and the other end overlapping with the TSS²⁰ of an expressed gene²⁷). The most significant HiC-ACT peaks have approximately 1.4–2 times the odds of overlapping an E-P interaction than the same number of most significant FitHiC2 peaks. Figure 6A displays the number of peaks overlapping E-P interactions for each enhancer database and method, as well as the corresponding odds ratio estimates and p values.

Figure 6.

Comparing HiC-ACT and FitHiC2 peak calls with dbSUPER super-enhancers and FANTOM5 enhancers in mESC data

(A) The number of interactions called by HiC-ACT and FitHiC2 that overlap with an enhancer-promoter (E-P) interaction (one end overlapping with an enhancer and the other end overlapping with the TSS of an expressed gene). More HiC-ACT peaks overlap with an enhancer than FitHiC2 peaks among their respective most significant 100,000, 250,000, and 500,000 interactions. Odds ratios are reported along with their statistical significance (p value).

(B) The total number of E-P interactions identified by each method for the enhancers in the dbSUPER and FANTOM5 databases. Since some enhancers may interact with multiple promoters, the total number of unique enhancers among the identified E-P interactions is also reported. The dashed gray line indicates the total number of enhancers in the database.

We next examined the total number of unique E-P interactions identified by each method for the enhancers in the dbSUPER and FANTOM5 databases (Figure 6B). HiC-ACT identifies 198 more dbSUPER SE-P interactions and 29,632 more FANTOM5 EP interactions than FitHiC2. Further, one enhancer may interact with multiple promoters, so we also report the total number of unique enhancers among the identified E-P interactions. Interestingly, all FitHiC2-identified dbSUPER enhancers and all but 14 FitHiC2-identified FANTOM5 enhancers are also identified by HiC-ACT.

Discussion

Hi-C has been widely adopted to study chromatin spatial organization with several peak callers proposed and commonly used to analyze and interpret this data. Here, we present HiC-ACT, a method to improve the detection of chromatin interactions by post-processing 3D peak calling results from methods relying on the assumption that pairs of chromatin interactions are statistically independent. HiC-ACT leverages the power of an aggregated Cauchy test to specifically account for the correlation without requiring any information about its structure. We demonstrated that HiC-ACT can improve sensitivity while maintaining comparable precision. We also provide guidelines regarding decision rules to maintain a desired type I error.

As expected, we observed most pronounced improvement over FitHiC2 when sequencing depth is less than 1 billion reads, which is the typical depth for the vast majority of Hi-C datasets generated to date. As shown through our analyses of the GM12878 data, the performance of FitHiC2 decreases as sequencing depth decreases; therefore, there is relatively more room for improvement for Hi-C data with lower sequencing depth. Further, Hi-C data with shallower sequencing depths are more likely than Hi-C data with higher sequencing depths to have lower signal-to-noise ratios for some significant interactions, and by borrowing information from neighboring interactions, HiC-ACT is able to more powerfully identify these interactions than FitHiC2. Even with increasing sequencing depth anticipated in some future Hi-C studies, we consider HiC-ACT useful because it will allow more powerful 3D peak calling at finer resolution (e.g., 5 kb or even 1 kb resolution, particularly when cut with the appropriate restriction enzymes such as the 4-base pair cutter MboI or DpnII).

It is unsurprising that the most significant interactions called by each method are different. Intuitively, all bin pairs in the neighborhood of a biologically relevant interaction are more likely to be significant than randomly colliding bin pairs. However, in Hi-C data with shallower sequencing depths, the signal strengths for all bin pairs in the neighborhood may not be adequately reflected in the unsmoothed p values. We have demonstrated that HiC-ACT has higher power to detect peaks with lower signal-to-noise ratio than FitHiC2 (Figure 3). Accordingly, for highly significant interactions, HiC-ACT is more likely than FitHiC2 to call peaks in its neighborhood as well, lending to the differences observed in the top peak calls of each method.

We note that although FastHiC accounts for spatial dependency, it is not intended to be used as a chromosome-wide peak caller in high resolution Hi-C data, such as FitHiC2. We find that FastHiC underperforms both HiC-ACT and FitHiC2 in this scenario (Figure S4). Although HiC-ACT can theoretically be applied to HiCCUPS results, we consider such application inappropriate because of the intrinsic nature of HiCCUPS to call summits in peak regions. HiCCUPS contrasts each chromatin loci pair with its local neighborhood; however, our goal is to call peaks by borrowing information from the neighborhood.

HiC-ACT is computationally efficient and scalable. HiC-ACT can process 25,000 pairwise interactions in ∼6 min with ∼2 GB memory and 0.5 million pairwise interactions in ∼2 h with ∼30 GB memory by using a 2.50 and 3.40 GHz Intel processor, respectively. Note that chromosome 1 has ∼90,000 and ∼168,000 pairwise interactions, at 10 kb resolution, passing the suggested initial p value filter in the ∼0.5 and ∼1 billion raw reads GM12878 Hi-C data, respectively.

Future work may involve fine tuning the smoothing parameter, particularly for 1 kb bin resolution Hi-C data, and investigating different weight functions.

By identifying statistically significant long-range interactions with enhanced statistical power and improved computationally efficiency, HiC-ACT can improve our knowledge regarding regions with regulatory potential and aid to establish links between cis-regulatory regions and their target genes. We anticipate HiC-ACT will become a convenient tool for many researchers.

Data and code availability

This paper did not generate any datasets.

Declaration of interests

The authors declare no competing interests.

Published: February 4, 2021

Web resources

ENCODE, https://www.encodeproject.org/

FANTOM5, https://fantom.gsc.riken.jp/5/

GEO, https://www.ncbi.nlm.nih.gov/geo/

HiC-ACT, https://github.com/tmlagler/hicACT

HiC-ACT, https://yunliweb.its.unc.edu/hicACT/