Similarities and Differences between Crystal and Enzyme Environmental Effects on the Electron Density of Drug Molecules

Abstract

The crystal interaction density is generally assumed to be a suitable measure of the polarization of a low‐molecular weight ligand inside an enzyme, but this approximation has seldomly been tested and has never been quantified before. In this study, we compare the crystal interaction density and the interaction electrostatic potential for a model compound of loxistatin acid (E64c) with those inside cathepsin B, in solution, and in vacuum. We apply QM/MM calculations and experimental quantum crystallography to show that the crystal interaction density is indeed very similar to the enzyme interaction density. Less than 0.1 e are shifted between these two environments in total. However, this difference has non‐negligible consequences for derived properties.

The polarization of a drug molecule in an enzyme environment can be approximated by the polarization of the same molecule in its small‐molecule crystal structure. The degree of similarity is quantified in this study for a model compound of the protease inhibitor loxistatin acid in its interaction with cathepsin B by using interaction densities and interaction electrostatic potentials.

Introduction

Molecular recognition between an enzyme and a low‐molecular weight ligand is a key feature in the mode of action of biologically active molecules, and in consequence the most important factor in drug design. ^[1] The main components of molecular recognition are steric and electrostatic complementarity between the enzyme pocket and the active molecule. If the recognition process is simplified from the induced‐fit theory to the classic key–lock mechanism, ^[2] small‐molecule crystal structures can be used to approximate the correct three‐dimensional shape of the active molecule in the biological environment. In both a biological as well as a crystalline environment, the small molecule will conformationally adapt its shape to the prevailing intermolecular binding forces, so that the resulting bound state reflects both its inherent flexibility and the environment.[ ³ , ⁴ ] Pascard states that “in numerous cases, there is a nearly perfect correlation between small‐molecule structural results, and the observed binding in receptor‐substrate complexes”. ^[5] Such similarities, investigated many times at the geometrical level, ^[6] have led to the development of the method of composite crystal‐field environments by Klebe ^[7] and SuperStar ^[8] as part of the Cambridge Structural Database suite of software.

Electrostatic complementarity between an enzyme binding site and an active molecule is an aspect that goes beyond geometry and molecular conformation since the electrostatic potential is inherently related to the electron density distribution of each partner. ^[9] Electron densities of biologically active small molecules can computationally be estimated in different environments (isolated state, solution, crystalline state) or modeled from experimental X‐ray diffraction structure factors. ^[10] Experimental electron–density determinations of crystals of low‐molecular weight enzyme ligands give a detailed insight into intermolecular interactions which are relevant for the biological recognition process such as electrostatic forces, hydrogen bonding or van der Waals interactions. ^[11] Consequently, the numerous experimental electron‐density investigations of biologically active compounds were justified by assuming that the polarization of the molecule under scrutiny reflects the polarization in the enzyme. ^[12] However, this underlying assumption has only rarely been investigated,[ ¹⁰ , ¹³ ] and, to the best of our knowledge, never been quantified. In this study, we quantify the extent of similarity between the electron‐density distributions of a model compound of the drug E64c as computationally determined in vacuum, in aqueous solution, in the corresponding cathepsin B enzyme complex and in the crystal structure of the pure molecule. The electron‐density distribution of the compound in its crystal structure was also determined from a low‐temperature high‐resolution synchrotron X‐ray diffraction study.

The epoxysuccinyl peptide loxistatin acid (E64c) is a derivative of the natural product E64 ^[14] and a potent inhibitor of papain‐like cysteine proteases (CAC1 enzymes). ^[15] E64c irreversibly inhibits proteases through nucleophilic epoxide ring opening and formation of a new C−S covalent bond with the respective cysteine thiol group. This mode of action has been supported by mechanistic studies ^[16] based on the E64c‐cathepsin B complex crystal structure. ^[17] Furthermore, the crystal structure of the pure E64c ligand alone was determined in 2015. ^[4] It was envisaged that this ligand would be ideal for the anticipated experimental study examining the similarities and differences between the polarization of the electron density of a drug molecule in its crystal structure to that in an enzyme since so much computational information about E64c is available.[ ¹³ , ¹⁴ ] However, the four independent molecules of E64c in its crystal structure are related by pseudo‐symmetry and are heavily disordered, which makes them unsuitable for experimental electron‐density determinations. ^[4] In turn, the E64c model compounds that were in fact suitable for experimental ED investigations ^[18] do not fit into any of the known cysteine proteases targeted by E64c (in vivo or in silico) preventing a comparison between the crystal and enzyme environments. To overcome these challenges, we recently devised an alternative strategy which first involved synthesis of the model molecule (2S,3S)‐3‐aminocarbonyl‐oxirane‐2‐carboxylic acid (1H). ^[19] As in E64c, this new substrate contains both the required electrophilic epoxide moiety for the reaction with cysteine and the carboxyl anchor group for initial binding into the enzyme pocket.

At physiological pH values, the carboxylic acid group in E64c is deprotonated and hence binds to cathepsin B as a carboxylate anion. Therefore, in the present study we also deprotonated 1H yielding the anion 1 (Figure 1 a), which crystallizes as a potassium salt with one molecule of co‐crystallized water (1K⋅H₂O, Figure 1 b). Water is abundant in the E64c‐cathepsin B complex, too, and the K⁺ ion in the crystal structure replaces the histidinium residue of cathepsin B in the complex, so that the type of intermolecular interactions in the crystal studied here can be expected to mirror those inside cathepsin B (section “Comparison of intermolecular interactions” in Results and Discussion). A single crystal of 1K⋅H₂O was measured to high resolution using synchrotron radiation at BL02B1, SPring‐8, and the electron‐density distribution was subsequently modelled experimentally. For this purpose, we employed X‐ray Wavefunction Refinement (XWR, ^[20] ), a novel technique combining Hirshfeld Atom Refinement (HAR, ^[21] ) and X‐ray constrained wavefunction (XCW) fitting.[ ²² , ²³ ] In silico, the small anion 1 fits into the binding pocket of cathepsin B, so that its electron density could be compared between the following environments: in the crystal structure (from XWR, model X; from QM/MM calculations, model C for crystal; embedded in a self‐consistent field of cluster point charges, model CC for cluster charges), inside the enzyme cathepsin B (from QM/MM calculations, model P for protein), in solution (COSMO solvation model S) and in vacuum (model G for gas phase).

Figure 1.

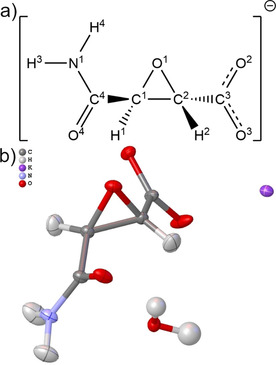
a) Illustration and atomic numbering of the (2S,3S)‐3‐aminocarbonyloxirane‐2‐carboxylate anion (1). b) Refined structure of the formula unit 1K⋅H₂O after HAR. All hydrogen atom positions and the isotropic displacement parameters for the water hydrogen atoms were freely refined. Anisotropic hydrogen displacement parameters in 1 were estimated with Shade2 ^[31] and fixed during the HAR. All displacement parameters are drawn at a 50 % probability level with the software Olex2. ^[32] The refined intramolecular geometry is as follows: C1−O1=1.4221(6), C2−O1=1.4306(6), C1−C2=1.4761(7), C2−C3=1.5204(7), C3−O2=1.2696(6), C3−O3=1.2351(7), C1−C4=1.5116(6), C4−O4=1.2286(6), C4−N1=1.3372(6), C1−H1=1.064(17), C2−H2=1.070(18), N1−H3=1.087(19), N1−H4=1.030(19), O${}^{\mathrm{H}{}_2\mathrm{O}}$ −H=0.95(2)/0.96(2) Å; C1‐O1‐C2=62.32(3), C1‐C2‐O1=58.56(3), C2‐C1‐O1=59.12(3), O2‐C3‐O3=126.13(5), H‐O${}^{\mathrm{H}{}_2\mathrm{O}}$ ‐H=108.0(18) °.

Intermolecular interactions between molecules lead to a polarization of each molecular electron density. In crystallography, the interaction density is defined as the difference between the electron density of a molecule in a crystal and the electron density of the same molecule with identical geometry in an assembly of non‐interacting molecules (in vacuo model). In biology, the difference between the molecule bonded to the active site and the molecule solved in water outside the active site is decisive. Nevertheless, the interaction density of biologically active small molecular compounds has often been used as a first approximation to the polarization of the ligand in the enzyme. For example, Dittrich and Matta argue that the “interaction density can be seen as an idealized situation that is analogous to drug‐receptor interactions and the redistribution of electron density of a drug molecule in the active site.” ^[24]

It is an open question if the magnitude of the interaction density is inside or outside experimental errors for charge‐density experiments, which means it is unclear if the interaction density can be measured. ^[25] Most of the discussion in the past was focused on the accuracy of the multipole model for extracting interaction‐density characteristics. ^[26] Alternatively, the interaction density was calculated based on periodic‐boundary theoretical computations. ^[27] Only very recently, an alternative approach to the derivation of the interaction density was discussed, namely the comparison of the non‐fitted and maximally fitted molecular wavefunction according to the X‐ray constrained wavefunction fitting technique. ^[28] The non‐fitted wavefunction produces the in vacuo electron density of the molecule under examination, whereas the fitted wavefunction includes the polarization of the molecule by the crystalline environment via the measured X‐ray structure factors. This new method was described mainly for an application to theoretically calculated X‐ray structure factors. In this work, we test this method against experimental structure factors for the compound 1K⋅H₂O (section “Interaction density and interaction electrostatic potential” in Results and Discussion).

Although the interaction density directly reflects the polarization of the molecule by its environment, for the molecular recognition process the electrostatic potential is the crucial property. Electron density and electrostatic potential are fundamental properties of a wavefunction and in this study both are calculated directly from the (experimentally constrained) wavefunctions. Beyond this relationship, there are also interesting similarities and differences between the topologies of their scalar fields and how these are interpreted with respect to chemistry and biology. ^[29] However, to the best of our knowledge, the electrostatic‐potential analogue to the interaction density has never been explored before. We refer to this difference between in vacuo and crystal electrostatic potential as interaction electrostatic potential (or simply interaction ESP) since the term interaction potential has a different meaning in the framework of QM/MM calculations. ^[30]

As discussed above, interaction density (and consequently also interaction ESP) are crystallographic terms, denoting the difference between the crystalline and the in vacuo states at identical geometry. However, for the simplicity of the argument, here we generalize both terms to denote the difference between the polarized (crystal X or C or CC, enzyme P, solution S) and unpolarized (in vacuo, gas phase, G) states at identical geometry (section “Interaction density and interaction electrostatic potential” in Results and Discussion). In addition, we have developed a technique to compare the electron densities of different optimized molecular geometries, which will be introduced in section “Bond‐wise comparison of difference densities” (Results and Discussion). In section “Comparison of derived properties”, we compare derived properties such as the Laplacian of the electron density and atomic charges in different environments.

Results and Discussion

Comparison of intermolecular interactions

Initially, a comparison between the intermolecular interaction network of 1 inside cathepsin B and that inside the crystal structure of 1K⋅H₂O (Figure 2) is discussed. For that purpose, molecular dynamics (MD) input was prepared by taking the E64c‐cathepsin B complex crystal structure ^[17] and pruning off all atoms of E64c that are not part of the simplified 1. After initial equilibration in a water box, molecular dynamics were simulated over 5 ns. The interaction of the carboxylate group with His⁺‐199 and Cys‐29 (Figure 2, left) is the electrostatic anchor that keeps 1 closely bonded inside the enzyme pocket during the entire time of the simulation (Figure 3, O₃‐HN${}_{\mathrm{His}{}^{+}-199}$ ). The contact with carboxylate atom O2 importantly keeps Cys‐29 close to the epoxide ring, eventually resulting in an interaction between the sulfur atom of Cys‐29 and the epoxide carbon atom 1, which prepares the ring‐opening reaction of E64c to irreversibly form a covalent C−S bond and inactivate the cysteine protease. ^[16] Figure 3 shows that the C₁−S_Cys‐29 contact remains stable throughout the MD simulation with 1 in cathepsin B implying that the model compound used here indeed represents the major characteristics of E64c as it would act in the same bonding environment. However, the amine group of 1 points into the artificially produced cavity, produced by shortening of the ligand compared to E64c, which is now filled with water molecules. Figure 2, left, shows that the nearest enzyme residues are Gly‐27 and Gly‐74, but as can be seen in Figure 3, these contacts are rather long, giving rise to conformationally flexible and rotating amide groups.

Figure 2.

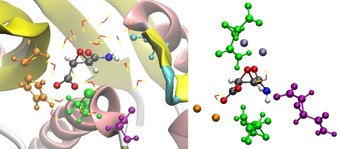
Visualization of close contacts of 1 in P (left) and X (right). Coloring according to interaction type. Orange: His⁺‐199/ K⁺ around carboxylate; green: Cys‐29/ 1 (symmetry‐generated) around epoxide and carboxylate; purple: Gly‐27/ 1 (symmetry‐generated) around amine; cyan/blue: Gly‐74/ K⁺ around carbonyl in amide group. Water is depicted as red‐and‐yellow sticks.

Figure 3.

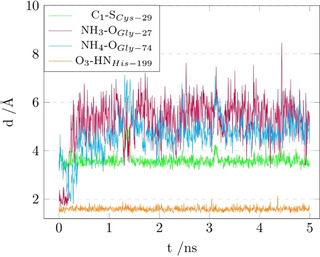
Plot of the distance between 1 and the four closest amino‐acid residues of the cathepsin‐B pocket (as visualized in Figure 2, left) during the 5 ns MD simulation of 1 inside cathepsin B.

Geometry snapshots were taken every 250 ps along the MD simulation between 4 and 5 ns. Starting from these, a total of four different QM/MM geometry optimizations were carried out. The resulting geometries are similar but not identical due to the multi‐minima nature of protein conformations. Table 1, left column, shows that the highest deviations for the various intermolecular contacts of the four final geometries vary between 0.16 and 0.01 Å, so that it is meaningful to report and interpret their average for a direct comparison between the protein and crystal environments (yielding model P for the following sections).

Table 1.

Closest contacts with the environment inside cathepsin B (left) and inside the crystal structure of 1K⋅H₂O (right). For hydrogen bonds d−H⋅⋅⋅A, the distances refer to the donor‐acceptor distances D⋅⋅⋅A. For the atom labeling, see Figure 1 a.

1 in cathepsin B		1 in 1K⋅H2O
Contact	Distance [Å][a]	Contact	Distance [Å][b]
O1⋅⋅⋅H−O${}^{\mathrm{H}{}_2\mathrm{O}}$	2.89 (4)	O1⋅⋅⋅K+	2.9092 (4)
N1−H3⋅⋅⋅O${}^{\mathrm{H}{}_2\mathrm{O}}$	2.76 (7)	N1−H3⋅⋅⋅O2	3.0157 (6)
N1−H4⋅⋅⋅O${}^{\mathrm{H}{}_2\mathrm{O}}$	2.98 (16)	N1−H4⋅⋅⋅O2	3.0443 (6)
O2⋅⋅⋅H−O${}^{\mathrm{H}{}_2\mathrm{O}}$	2.69 (4)	O2⋅⋅⋅H−O${}^{\mathrm{H}{}_2\mathrm{O}}$	2.7468 (6)
O3⋅⋅⋅H−N${}^{\mathrm{His}{}^{+}\text{-}199}$	2.69 (3)	O3⋅⋅⋅K+	2.6210 (5)
O4⋅⋅⋅H−O${}^{\mathrm{H}{}_2\mathrm{O}}$	2.65 (1)	O4⋅⋅⋅K+	2.6925 (4)

[a] The distances are the average of 4 QM/MM optimized geometries (see Experimental Section). The numbers in brackets are the sample standard deviations in the last shown digit(s). [b] The distances are the crystallographically refined geometries from the XWR procedure. The numbers in brackets are the standard uncertainties in the last shown digit from the refinement.

For every hydrogen bonding donor or acceptor, there is either a hydrogen bond or an electrostatic contact in both these environments. The carboxylate group (atoms O2 and O3) forms one hydrogen bond with water as acceptor and one contact dominated by electrostatics (either positive histidinium ring or positive K⁺ ion) each. The amine group forms two hydrogen bonds to water inside the enzyme pocket, and two hydrogen bonds to a symmetry‐generated carboxylate atom O2 in 1K⋅H₂O. The epoxide oxygen atom O1 forms a hydrogen bond or an electrostatic contact to K⁺, respectively, with the same distance of 2.9 Å. Remarkably, the longest of the contacts coincide in both environments, and the shortest one in 1K⋅H₂O coincides with the second‐shortest one in the enzyme, which is, however, the most important one, namely the electrostatic anchor identified in Figure 3.

In summary, a qualitative comparison of the intermolecular interaction networks in both crystal and enzyme environments shows some systematic similarities that lead us to believe that a comparison of the polarization of the electron density in both environments will be meaningful. However, Figure 2 also shows that the conformations of the carboxylate and the amide groups in both environments are significantly different, so that a direct comparison of the electron densities belonging to individual bonds will be difficult. This problem will be tackled in section “Bond‐wise comparison of difference densities”, whereas the next section deals with the interaction densities and interaction electrostatic potentials of the entire anion 1.

Interaction density and interaction electrostatic potential

The interaction densities (Figure 4) and interaction electrostatic potentials (ESPs, Figure 5) were calculated according to the ideas discussed in the Introduction. They represent the differences between anion 1 in its polarized (crystal X or C or CC, enzyme/protein P, solution S) and unpolarized (in vacuo, gas phase, G) states at identical geometry. In detail, Figures 4 and 5 depict the following model differences:

Figure 4.

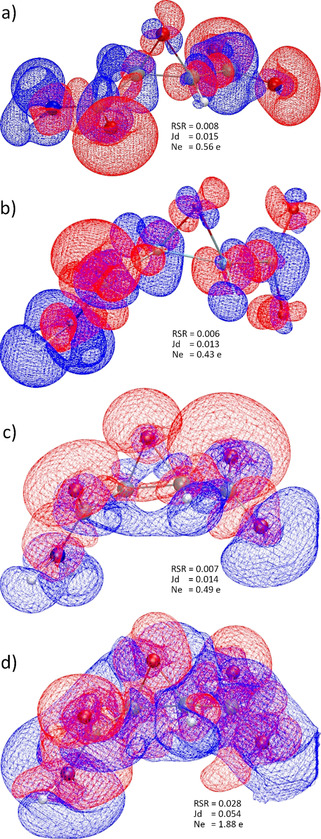
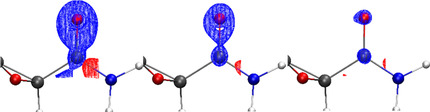
Isosurfaces of interaction densities at ±0.0067 e Å⁻³. Red regions correspond to higher ED compared to the in vacuo state, blue to lower ED. a) Protein env.: P minus G at geom. P; b) crystal env.: C minus G at geom. C; c) cluster charges: CC minus G at exp. geom.; d) X‐ray constrained wavefunction: X minus G at exp. geom. RSR=real‐space R‐value. Jd=Jaccard distance. Ne=integrated number of electrons in the difference grid file. All isosurface representations are generated with VMD. ^[36]

Figure 5.

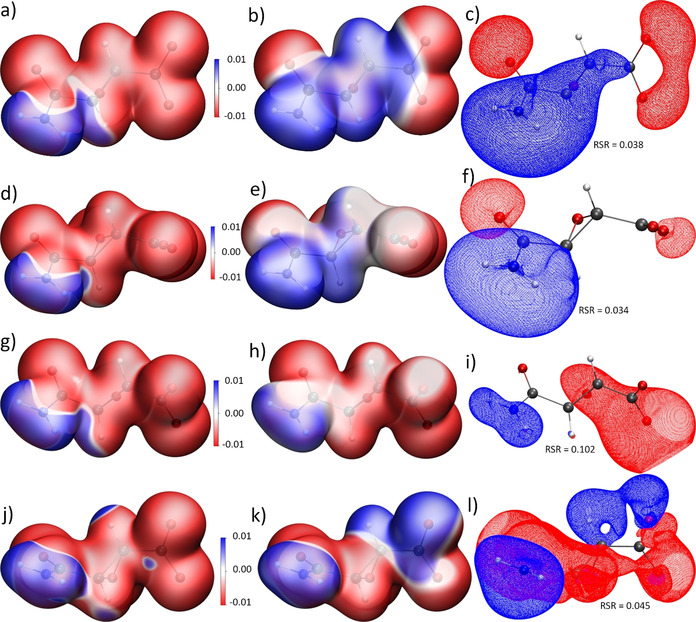
Left column (a,d,g,j): 0.01 a.u. isosurface of the ED with total ESP mapped onto it, capped at ±0.01 e Å⁻¹. Middle column (b,e,h,k): 0.01 a.u. isosurface of the ED with interaction ESP mapped onto it, capped at ±0.01 e Å⁻¹. Right column (c,f,i,l): Isosurfaces of the interaction ESP at ±0.028 e Å⁻¹, except for i) with +0.014 and −0.070 e Å⁻¹. Red corresponds to more negative regions compared to the in vacuo state, blue to more positive regions (compare color scale). a) Protein env.: P at geom. P; b,c) Protein env.: P minus G at geom. P; d) crystal env.: C at geom. C; e,f) crystal env.: C minus G at geom. C; g) cluster charges: CC at exp. geom.; h,i) cluster charges: CC minus G at exp. geom.; j) X‐ray constrained wavefunction: X at exp. geom.; k,l) X‐ray constrained wavefunction: X minus G at exp. geom. RSR=real‐space R‐value of the interaction ESP. (Units: 1 e Å⁻¹=14.40 V.)

1. 4 a/5 b,c: model P minus model G at the QM/MM‐optimized geometry of P;

2. 4 b/5 e,f: model C minus model G at the QM/MM‐optimized geometry of C;

3. 4 c/5 h,i: polarization of 1 with a cluster of Hirshfeld‐atom point charges and dipoles (model CC, cluster charges) minus model G at the experimental geometry from X‐ray diffraction;

4. 4 d/5 k,l: effect of X‐ray constrained wavefunction fitting:[ ²² , ²⁸ ] X‐ray constrained model X minus model G at the experimental geometry from X‐ray diffraction.

In the QM/MM calculations, only 1 was treated quantum‐mechanically, but everything else including water and potassium ions was treated with molecular mechanics, so that the polarization features seen in Figures 4 a,b and 5 a–f are purely caused by electrostatics, with limited dispersion and no covalent component. The calculations of Figures 4 c,d and 5 g–l, however, required the definition of at least the asymmetric crystal unit, which explicitly includes water and potassium ions. In the Experimental Section, we describe the methodology developed here to isolate only the electrostatic component of the interactions.

The interaction densities in Figures 4 a,b look visually similar. The similarity is even more obvious in the interaction ESP plots, comparing Figure 5 b with 5 e and 5 c with 5 f. It must be noted that the conformations of the amide and carboxylate groups are different in crystal and enzyme environments, so that the lobes around the carboxylate group in Figure 5 f need to be turned by 90° to match the shape of the lobes in Figure 5 c. This means that the same functional groups are qualitatively polarized in the same way in both environments P and C. For example, all oxygen lone pairs show red regions in the interaction densities and ESPs, which means that they accumulate electron density and become more negatively polarized in the P and C environments than in the in vacuo state G. All hydrogen atoms are covered in blue surfaces, which means that they lose electron density relative to the isolated state. Both effects are due to interaction with neighboring non‐covalent bonding partners, for example, via hydrogen bonding, which is characterized by charge transfer.

In absolute numbers, the polarization effect on the ED and ESP is small; the difference values are low. For the interaction density, the maximum value in the grid file is ±0.1 e Å⁻³ compared to maximum values of up to 265 e Å⁻³ in the grid file of the total ED. For the interaction ESP, the maximum values in the grid file are ±0.08 e Å⁻¹ compared to maximum values in a range of [−0.31, 782] e Å⁻¹ for the total ESP. A meaningful isovalue for the representation of the interaction densities is 0.0067 e Å⁻³, whereas it is around 0.03 e Å⁻¹ for the interaction ESP. The real‐space R‐values (RSR) and Jaccard distances (Jd) are still close to zero. (For a definition of these quantities, please see the Experimental and Computational Section.) An integration of the absolute values of the interaction density inside the grid files (N _e=number of electrons) is a measure of the charge transfer caused by the polarization. A total of 0.56 electrons are shifted in the protein environment and 0.43 e in the crystal environment (Figures 4 a and b), indicating that, overall, 1 is slightly more polarized by the enzyme than the crystal.

Dittrich et al. suggested to use different point‐charge and ‐dipole models to simulate the crystal field effect and produce the interaction density. ^[27c] Following this idea, we used a self‐consistent Hirshfeld cluster‐charge model as it is normally employed in Hirshfeld Atom Refinements.[ ^21b , ³³ ] Figure 4 c) shows the effect of this field on the ED: qualitatively, the regions of accumulation and depletion are the same around oxygen and hydrogen atoms in comparison to the QM/MM results, and quantitatively, RSR, Jd and Ne values are in‐between the respective values for the QM/MM results. However, the regions of ED polarization are wider and more diffuse. This has strong consequences on the ESP, see Figures 5  h and i. The polarization of all the oxygen atoms by the surrounding positive point charges is much stronger than in the QM/MM models: the negative isovalue in Figure 5 i is 2.5 times higher and the RSR value is 3 times higher. Hence, it is clear that the Hirshfeld cluster‐charge model overestimates the polarization effect by the crystal field.

Finally, following an idea by Ernst et al., ^[28] we have employed XCW fitting against the experimental synchrotron X‐ray structure factors of 1K⋅H₂O to map the crystal field effect on 1. The experiment contains more information, for the better or worse, than the quantum‐mechanical ansatz used for the XCW. Beyond polarization via the crystal field, additional effects are electron correlation, ^[34] and, unfortunately, systematic errors, with radiation damage being the most important one here. These effects are also included into the X‐ray constrained wavefunction, so that the result is not a pure interaction density or interaction ESP. ^[23] However, since a hybrid‐DFT functional was used in the fitting, we assume that the majority of the electron correlation effect is included already in the unperturbed wavefunction before fitting, so that the major effect presented here is indeed due to the crystal field and the experimental error.

Figure 4 d shows that the effect of the XCW fitting on the ED is much more pronounced than that of the theoretical models where the polarization effect could be treated in an isolated way. The spread of the isosurfaces as well as the RSR and N _e values are much larger, showing that 1.88 e are shifted between the unperturbed and the fitted wavefunction, which is nearly four times more than in the QM/MM and point‐charge models. However, qualitatively the experimental information is still meaningful as the polarization pattern in the interaction density is still the same (red at oxygen, blue at hydrogen, see also representations at different isovalues in the Supporting Information, Figures S8). In the interaction ESP (Figures 5 k,l), the polarization of the carboxylate group is unsymmetrical, that is, one oxygen atom becomes more and one less negatively polarized in the crystal environment, which is the only qualitative difference to the theoretical results in Figures 5 a–i. The RSR value of 0.045 is close to those of the QM/MM calculations.

The high‐resolution low‐temperature synchrotron X‐ray diffraction data of 1K⋅H₂O used in this study were prone to radiation damage, which was corrected with a scaling procedure (see Supporting Information). It is conceptually difficult within XCW fitting to determine to what extent the data quality is affected, which will in turn affect the results presented here. Therefore, we decided to perform a multipole modeling according to Hansen and Coppens ^[35] on the experimental and on additional theoretically calculated structure factors with the sole purpose of separating model from data effects, which is discussed in detail in the Supporting Information. We find that significant discrepancies are caused by the model used to treat the experimental data and not by data inaccuracy alone.

In summary, qualitatively and quantitatively the polarization of the electron density and the ESP of 1 in crystal and enzyme environments is similar, with a slightly larger effect in the enzyme. Hirshfeld cluster charges overestimate the crystal field effect, whereas XCW fitting against the experimental structure factors captures the effect with a strong bias in the ED and a smaller bias in the ESP. Since every model for experimental X‐ray data treatment, such as the XCW or the multipole model, includes theoretical assumptions, and since the data always consist of a convolution of many physical effects, we believe that the refinement of experimental data might be useful, but data can never simply be trusted, as also demonstrated in ref. ^[37] In this context, multipole‐model derived electron densities were compared to the crystal electron densities calculated from QM/MM approaches at various different levels of theory in previous studies.[ ³⁸ , ³⁹ , ⁴⁰ ] However, it remains unclear, here and in general, whether the level of data accuracy and the convolution of different physical effects in the data yields physically useful and meaningful derivations of the interaction density and ESP from the experiment.[ ²⁵ , ²⁶ ] Therefore, in the next section we concentrate on details of the difference densities from theory alone.

Bond‐wise comparison of difference densities

One disadvantage of the interaction density is the reference to isolated in vacuo systems. Therefore, we now use difference densities that use the protein environment as reference. However, a conceptual difficulty to overcome is that such comparisons are necessarily based on different molecular geometries. The molecular conformations of 1 obtained from geometry optimization in the crystal structure (QM/MM, model C), inside the enzyme cathepsin B (QM/MM, model P), in solution (COSMO, model S) and in vacuum (model G) are significantly different, as visualized in Figure 6 for the C and P geometries.

Figure 6.

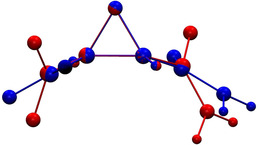
Superposition of the optimized molecular geometry of 1 in cathepsin B (model P, blue) and in the crystal of 1K⋅H₂O (model X, red).

To account for changes of bond distances and angles, only bond‐centered grids were analyzed that were chosen to be as small as possible and scaled to the respective bond lengths, that is, the sample point separation was adjusted relative to the bond lengths (Figure 7, more details in the Experimental and Computational Section). Following this approach, only minor contaminations of the difference densities in the corners of the boxes used to define the grids are observed.

Figure 7.

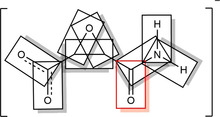
Visualization of bond‐centered scaled grids and the selection of all bonds of 1 used for the analysis. The C4−O4 bond is highlighted, which is the first entry in Figures 8 and 9.

It is expected that the effect of polarization is most pronounced for bonds that interact directly with the environment via hydrogen bonding. Whereas the carboxylate bonds C3−O2 and C3−O3 that carry the negative charge are less affected, Figure 8 shows the density differences for the most affected bonds C4−O4 and C4−N1. The discrepancy between models G and P is the largest, significantly reduced in the solvation model S, and nearly vanished in the crystal environment C. This implies that the crystal environment is indeed a good model of the larger enzyme environment. For the N−H bonds in Figure 8, the G‐vs.‐P difference is always the most pronounced as for the C−N and C−O bonds. However, the trend between S‐vs.‐P and C‐vs.‐P is more ambiguous. In addition, for the N−H bonds the impurities in the corners of the boxes are higher.

Figure 8.

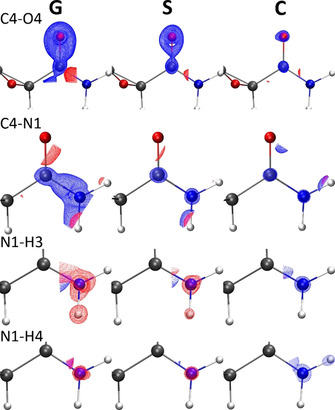
Isosurfaces of difference electron densities in bond‐centered scaled grids at ±0.054 e Å⁻³ (blue=positive, red=negative). Differences are shown for those four bonds where the effect is most pronounced (cf. Figure 9), and for the differences of the vacuum (G), solvent (S) and crystal (C) models always with respect to the enzyme (P).

Nevertheless, RSR values were calculated for every bond‐centered difference grid file and graphically summed up in Figure 9 for the same differences as in Figure 8 (G/S/C vs. P), but in addition the K⁺ countercation was explicitly included in the G and S calculations. K⁺ is located in proximity to the carboxylate group replacing the His⁺‐199 group in the protein environment (Figure S9 in the Supporting Information). This first polarization by K⁺ already reduces the differences between the G and the P environments, as it introduces a first polarizing field acting upon the molecule. This shows that the COSMO solvation model S produces already a good approximation to the polarization present in the enzyme, ^[13a] so the influence of K⁺ becomes negligible. However, the crystal environment is the best approximation to the protein environment, and if the bond N1−H4 was not an outlier, the effect would be visually even more compelling. In total, the similarity improves from an RSR sum of 0.171 for model G (w/o K) to 0.072 for model C, which is a drop of 0.1 RSR points or 58 %.

Figure 9.

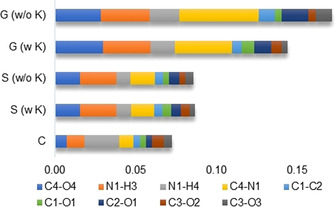
Sum of the RSR values for all bond‐centered difference density grid files as visualized in Figure 8 for the four most affected bonds. The differences of the vacuum model (G) with or without K⁺ countercation, the solvent model (S) with or without K⁺ countercation and the crystal model (C) are always calculated with respect to the enzyme model (P). See also Figure S10 in the Supporting Information.

Comparison of derived properties

As the second derivative of the electron density, the Laplacian is very susceptible to any method or model change. Therefore, we decided to plot it along the C4−N1 bond, which is the one most affected by the environmental influences as shown in Figures 8 and 9. Figure 10 shows the progression of the Laplacian along this bond for all different models including the Hirshfeld cluster‐charge model (CC) and the XCW‐fitted model (X). The minima at ca. 0.42 and 0.85 Å are the valence‐shell charge concentrations (VSCCs) inside this polar covalent bond. With the P‐results serving as the reference as in the previous section, the deeper VSCC at the nitrogen atom is well described by all theoretical models except the CC model, which overestimates the charge concentration. The experimental data in the XCW fitting model significantly deviate from all other results, producing a shift of the nitrogen VSCC by about 10 e Å⁻⁵ and 0.02 Å. This effect was previously observed and reported for the multipole model.[ ³⁸ , ³⁹ ]

Figure 10.

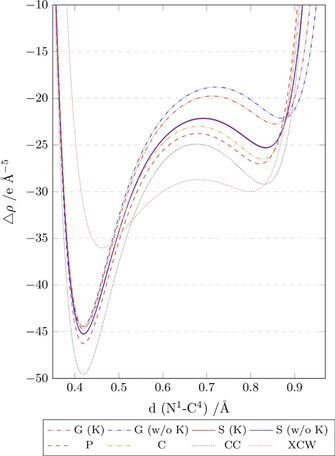
Laplacian of ED along the N1−C4 bond (plotted with the N atom at position 0 Å, left) for the vacuum model (G) with or without K⁺ countercation, the solvent model (S) with or without K⁺ countercation, the crystal model (C), the enzyme model (P), the Hirshfeld cluster‐charge model (CC) and the XCW fitting model (X). Values were calculated using Multiwfn. ^[41] .

The deviations of all models relative to the model P are best visible in the middle of the bond towards the carbon atom VSCC. Model G differs the most from the protein model P, which is slightly improved when the counter‐cation K⁺ is accounted for. The results are significantly closer to the reference model P for both solvation models (S), but the closest match exists between the crystal (C) and protein model. These findings agree with those in Figure 9 for the difference densities. The model CC has the most negative Laplacian value (highest electron concentration) of the theoretical models everywhere along the bond, but it is still closer to the models P and C than the model G. In contrast to the model CC, whereas the XCW fitting model shows the least negative Laplacian value for the nitrogen VSCC, it shows the most negative Laplacian value in the middle of the bond, deviating significantly from all other models. As discussed in section “Interaction density and interaction electrostatic potential”, it is difficult to know whether these deviations are caused by data inaccuracy or the convolution of many different physical effects—not only the crystal field effect whose treatment is the only difference between all the theoretical models. A comparison with Figure S7 in the Supporting Information shows, however, that the multipole model using both the experimental and theoretically generated structure factors leads to hugely different results of the Laplacian in this polar covalent C−N bond, and relative to that result the XCW fitting model agrees well with the theoretical models (compare a related discussion in ref. ^[42] ).

The atomic charges (Table 2, here calculated according to Bader's QTAIM ^[43] ) are directly related to the electrostatic potentials. All the oxygen atoms are most negatively charged in the protein environment, losing negative charge from models C toward model S, and being least negatively charged in the in vacuo state (models G). The same trend holds for the positive charges of the hydrogen atoms. For both oxygen and hydrogen atoms, the crystal environment C produces the atomic charges that are most similar to the protein environment. All these trends are reflected in the interaction ESP plots in the same way (Figure 5). For the carbon atoms, which are not involved in the hydrogen bonding network, the same trend is true, but less pronounced: the positive charges are highest in the P model and lowest in the G models.

Table 2.

QTAIM atomic charges (e) of atoms in each model. For atom labeling, see Figure 1 a. For model definition, see Figure 10. The isolated anion and the QM/MM models do not include explicit K cations, but there are two symmetry‐independent ones in the crystal structure (CC and XCW models).

Atom	G (w/o K)	G (w K)	S (w/o K)	S (w K)	C	P	CC	XCW
O1	−0.875	−0.852	−0.903	−0.898	−0.899	−0.907	−0.928	−1.140
O2	−1.212	−1.227	−1.257	−1.247	−1.267	−1.303	−1.346	−1.266
O3	−1.216	−1.230	−1.256	−1.245	−1.258	−1.304	−1.276	−1.389
O4	−1.151	−1.133	−1.193	−1.192	−1.222	−1.277	−1.225	−1.276
N1	−1.105	−1.126	−1.153	−1.152	−1.201	−1.165	−1.185	−1.563
C1	0.356	0.359	0.356	0.357	0.360	0.382	0.398	0.325
C2	0.335	0.364	0.341	0.346	0.349	0.390	0.377	0.637
C3	1.668	1.581	1.627	1.611	1.614	1.650	1.724	1.820
C4	1.350	1.404	1.409	1.412	1.393	1.407	1.500	1.583
H1	0.052	0.043	0.071	0.074	0.068	0.094	0.053	−0.010
H2	0.029	0.072	0.066	0.072	0.063	0.084	0.053	0.150
H3	0.387	0.396	0.445	0.446	0.506	0.495	0.457	0.647
H4	0.384	0.409	0.448	0.449	0.495	0.456	0.435	0.569
K	–	0.940	–	0.968	–	–	0. 960/ 0. 971	0.925/ 0.957

On average, the charges produced in the Hirshfeld cluster‐charge model (CC) are slightly higher than those in the QM/MM crystal model C, sometimes even higher than in the enzyme model P — an overestimation of the polarization already discussed with respect to Figure 5 h,i. However, the atomic charges produced after XCW fitting are significantly higher than the charges of any of the other models. Despite these discrepancies, chemically meaningful charge differences of the same element in different functional groups are always preserved. This refers to the lower negative charge of the epoxide oxygen atom O1 or the higher positive charges of the carboxyl and carbonyl carbon atoms C3 and C4 compared to the epoxide carbon atoms C1 and C2.

Conclusions

In this study, we used model compound 1 which consists of the pure deprotonated epoxysuccinyl peptide group that is the biologically active center of the drug loxistatin acid (E64c). In molecular dynamics simulations, 1 showed to exhibit the same stable intermolecular contacts inside the enzyme pocket of cathepsin‐B that lead to the irreversible inhibition of this protease by E64c. Moreover, in the crystal structure 1K⋅H₂O intermolecular interactions (hydrogen bonds and electrostatic contacts) are formed that are very similar to those in the enzyme pocket, involving biologically important water molecules and potassium cations. The K⁺ ion is located in the crystal where the His⁺ group is located in cathepsin B.

Detailed analyses of the interaction densities and electrostatic potentials as well as of the difference electron densities show unambiguously that the crystal environment, as described by QM/MM, is significantly more similar to the protein environment than any of the other environments (a cluster of Hirshfeld point charges and dipoles, a solvation model, or the isolated molecule in vacuum, the latter two with or without explicit perturbation by the K⁺ countercation). The difference between the integrated interaction densities in the protein and crystal environments was measured to be smaller than 0.1 e over the entire anion 1, or 0.075 units of the RSR value when integrated over all bonds of 1. We conclude that the sentiment often expressed in the literature that the interaction density in crystals of the pure substance is a measure of the polarization of the same molecule in the enzyme active site is true for the analyzed compound. We also showed that the interaction density can be used to predict the features of the electrostatic recognition process.

Finally, we investigated whether the above conclusion means that experimental electron‐density studies are an ideal tool to get deeper insight into the enzyme‐ligand interaction. Certainly, with an error‐free experiment and an ideal model to refine the experimental structure factors, such studies would be a close simulation of the biological situation. However, the crystal field effect on the electron density is relatively small, that is, less than one out of 67 electrons of 1 are shifted due to polarization. Therefore, the interpretation of the experimental results and maps is difficult relative to the idealized theoretical models. The accuracy of the data and the (in‐)flexibility of the model have a huge influence on the result. The convolution of many physical effects in the experimental data that might be lacking in the theoretical ansatz/model does not allow to unambiguously pin down the crystal field effect in the difference densities. Certainly, for an effect such as the polarization in different environments we cannot trust the experimental data blindly but have to critically assess them, when, simultaneously, a computationally relatively cheap and simple method such as a COSMO solvation model already approximates the results quite closely.

Experimental and Computational Section

The synthesis and spectroscopic characterization of 1K⋅H₂O has been reported previously. ^[19] Details of the synchrotron X‐ray diffraction experiment are given in Table 3. A high‐resolution measurement was carried out at beamline BL02B1 of SPring‐8 using a helium gas‐stream for cooling down to 25 K and a large curved image plate for detection. The data resolution was limited to d=0.45 Å after radiation‐damage problems were observed, which was corrected by using a scaling procedure in the software RapidAuto ^[44] (see more details in the Supporting Information). The crystal structure of 1K⋅H₂O was solved using ShelxT ^[45] and refined using olex2.refine and Tonto ^[46] within the NoSpherA2 framework. ^[47] HAR was performed on a level of theory of B3LYP/def2‐TZVP using a radius of cluster charges and dipoles of 20 Å. Anisotropic displacement parameters of hydrogen atoms of 1 were determined using the SHADE2.1 webservice, ^[31] and then iteratively updated in Shade in‐between HAR cycles, whereas the hydrogen atoms of the water molecule were refined with isotropic displacement parameters. Deposition number 2024395 contains the supplementary crystallographic data for this paper (crystal structure of 1K⋅H₂O, the conditions and the parameters used in the HAR as well as the structure factor magnitudes). These data are provided free of charge by the joint Cambridge Crystallographic Data Centre and Fachinformationszentrum Karlsruhe Access Structures service www.ccdc.cam.ac.uk/structures.

Table 3.

Crystal, measurement, and refinement details for 1K⋅H₂O.

	HAR	XCW
empirical formula	C4H6KNO5
formula weight [g mol−1]	187.20
cell setting, space group	trigonal, P312 (No. 152)
Z	6
T [K]	25
unit cell dimensions
a [Å]	8.14360(10)
c [Å]	19.1623(3)
V [Å3]	1100.55(3)
F(000)	576
crystal size [mm3]	0.15×0.11×0.10
crystal form, color	block, colorless
wavelength λ [Å]	0.3532
absorption correction	multi‐scan
absorption coefficient μ [mm−1]	0.115
T min/T max	0.884/1.206
max. θ (°)	23.103
(sin θ/λ)max [Å−1]	1.11094
measured, independent and observed reflns	62 635, 8415, 8362
completeness	100 %
redundancy	7.474
weighting scheme[a] w=	(σ 2+(0.048 P)2+0.162 P)−1	σ −2
R int	0.0327	–[b]
number of parameters	121	–
R 1(F)	0.0266	0.0200
R w(F)	0.0757	0.0208
R all(F)	0.0267	–[c]
N ref/N v	69.1	–
Δρ max, Δρmin [e Å−3]	1.371/−0.378	0.756/−0.216
Flack parameter	0.13(6)	–[b]
CCDC deposition no.	2024395	–

[a] With $P=\frac{F_o^2+2F_c^2}{3}$ . [b] Merged data. [c] Not reported by Tonto.

The final wavefunction calculation after the last structural least‐squares refinement in HAR serves as the model CC since it is a single‐point calculation under the influence of a surrounding cluster of self‐consistent Hirshfeld point charges and dipoles. Subsequent XCW fitting was performed using a level of theory of B3LYP/def2‐TZVP without cluster charges to include an estimate of the electron correlation effect into the wavefunction ansatz whereas the crystal environmental effect is fitted based on the experimental data. The resulting wavefunction serves as the model X (or XWR/XCW).

The final crystal structure was used to build a supercluster according to the symmetry of the crystal to perform QM/MM calculations in the crystal system (C), treating one anion 1 in the center of the cluster quantum‐mechanically and the proximity using molecular mechanics based on a CHARMM force field. Parameters describing 1 were obtained from the SwissParam webservice. ^[48] QM/MM structure optimizations were performed using NAMD2 and Turbomole in all cases during this study, interfaced using ChemShell.[ ⁴⁹ , ⁵⁰ , ⁵¹ , ⁵² , ⁵³ ] The level of theory used for the QM part was B3LYP/def‐TZVP. Previous studies were able to show that the density is sufficiently well described using triple zeta basis sets, and the extent of differences using different levels of theory in QM/MM are documented.[ ³⁸ , ³⁹ , ⁴⁰ ]

For a model of the protein environment, anion 1 was placed into the active site of cathepsin B, based on a protein crystal structure of the E64c—cathepsin B complex ^[17] already modified as MD input including all hydrogen atoms in ref. [13a]. The resulting geometry was then equilibrated and simulated with molecular dynamics (MD) at 310 K using a CHARMM force field for protein, water and salt ions.[ ⁵⁴ , ⁵⁵ , ⁵⁶ ] The geometries at four points during the simulation between 4 and 5 ns (250 ps apart) were taken to perform QM/MM geometry optimizations (NAMD, Turbomole, ChemShell), optimizing the geometry of 1 quantum‐mechanically on a level of theory of B3LYP/def‐TZVP, and optimizing the residues in proximity of 1 with at least one atom in a range of 3 Å with molecular mechanics. Since four slightly different geometries were the result of these calculations, the calculation of grids was performed on all wavefunctions and the arithmetic average of the geometries and the grid values were calculated for the comparisons between the different environments. All plots labelled as model P refer to these averaged grids.

Optimized geometries in solvation (S) and in vacuo (commonly called gas‐phase model, G) were obtained by ab‐initio optimizations using the level of theory B3LYP/def‐TZVP in Turbomole. ^[51] For model S, a COSMO solvation model of water was used. These calculations were carried out with anionic molecule 1, as well as with a potassium counter‐cation, to give an interaction partner as a first model of interaction with the environment.

The calculation of grid files of the interaction density and interaction ESP is simple, however, the setup of the boxes of the grid files for bond‐wise comparison between different geometries is difficult. We programmed an in‐house software (cuQCT, author: Florian Kleemiss) for the calculation and manipulation of grid files in the Gaussian cube format. Bond‐centered grid files are generated by first finding the midpoint between the two positions of selected atoms. The unit vector connecting them will provide the vector $\overrightarrow{a}$ of the box. A third atom is used to form a plane and to find the vector in this plane that is perpendicular to $\overrightarrow{a}$ . This way, the second vector for the grid is found, which will be called $\overrightarrow{b}$ . Both vectors are normalized to have a length of 1 bohr. The last vector $\overrightarrow{c}$ for the calculation of the grid is found by the calculation of the vector product of $\overrightarrow{a}$ and $\overrightarrow{b}$ The midpoint of the first two selected atoms will then be used as the central point of the grid. By choosing a multiplicator for the distance between atoms 1 and 2 in all three dimensions of the grid, the atoms in different grid files will always be located at the same position of the grids. The origin of the grid is then found by moving into the negative directions of $\overrightarrow{a}$ , $\overrightarrow{b}$ and $\overrightarrow{c}$ for half the corresponding length of the complete grid size from the central point. Then the calculation with a fixed number of grid points scales the grid vectors and allows comparability with grids in different settings or with different molecular geometry without interpolations.

To have a quantitative measure of similarity between two ED or ESP grids, a real space R value (RSR or R_RS) was used. The definition of the RSR was taken from the literature. ^[57] For the ED, it is defined as Equation 1:

$${\displaystyle R_{RS}=\frac{\sum \left|{\rho }_1\left(r\right)-{\rho }_2\left(r\right)\right|}{\sum \left|{\rho }_1\left(r\right)+{\rho }_2\left(r\right)\right|}.}$$ (1)

This RSR gives insight in the total difference in ED relative to the total ED of the compound. It is likewise defined for the ESP. A value of 1 corresponds to a total shift of the complete property, while 0 corresponds to perfect agreement. As an alternative, the weighted Jaccard or Soergel distance, ^[58] as a variation of the Jaccard distance for binary groups, ^[59] can be defined for the ED differences as Equation 2:

$${\displaystyle d_{Jaccard}=\frac{\sum \mathrm{m}\mathrm{i}\mathrm{n}\left({\rho }_1\left(r\right),{\rho }_2\left(r\right)\right)}{\sum \max \left({\rho }_1\left(r\right),{\rho }_2\left(r\right)\right)}}$$ (2)

where the sum runs over all grid points of the density.

The number of electrons shifted between two ED distributions is given by the sum over the whole grid with grid point indices i, j, k. The local density difference is multiplied with the voxel size (which is the triple product of the grid vectors) and divided by 2 since local depletion of electrons will accumulate in a different place [Eq. 3]:

$${\displaystyle N_e={\sum }_i{\sum }_j{\sum }_k\left[\frac{{\rho }_1\left(r\right)-{\rho }_2\left(r\right)}{2}\times \overrightarrow{a}\left(\overrightarrow{b}\times \overrightarrow{c}\right)\right].}$$ (3)

The wavefunctions for the models CC and X of the crystal system required the explicit inclusion of two potassium ions and a water molecule in the asymmetric units of the crystal structure dictated by the crystallographic symmetry. This is necessary to describe the cluster of charges correctly in the case of Hirshfeld point charges and to calculate correct structure factors in the case of XCW. However, for an optimum comparability with respect to the QM/MM calculations, the calculation of ESP and ED grid files for the models CC and X required a routine to calculate these grids without explicit, only implicit, contributions of the potassium ions and the atoms in water. In a new feature of cuQCT, these atoms were ignored for the calculation of ESP and ED by skipping all basis functions that are associated to these atoms while calculating the value of a molecular orbital at a point in space for the ED or during the integration of the density for the ESP.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

F. Kleemiss, E. K. Wieduwilt, E. Hupf, M. W. Shi, S. G. Stewart, D. Jayatilaka, M. J. Turner, K. Sugimoto, E. Nishibori, T. Schirmeister, T. C. Schmidt, B. Engels, S. Grabowsky, Chem. Eur. J. 2021, 27, 3407.