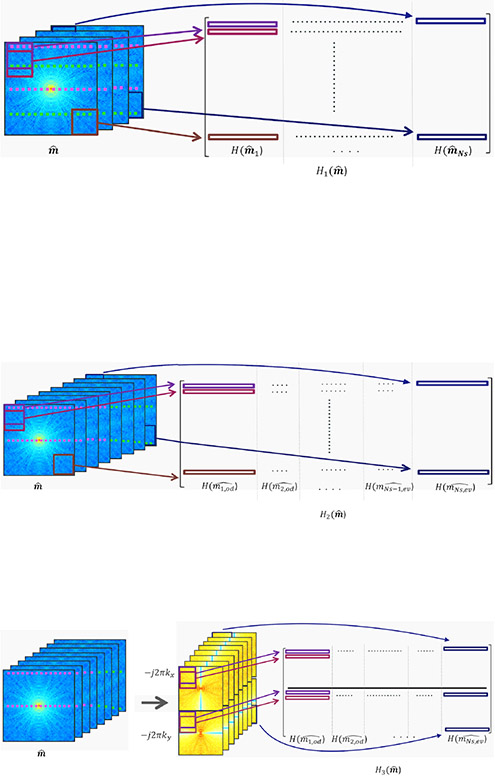
Fig. 1:

Construction of the block-Hankel structured low-rank matrices for various reconstructions

(a) The k-space data of each shot is stacked into a 3-D matrix. Using a moving filter of size r × r (marked by the rectanguar boxes), the k-space data is transformed (“lifted”) to form a structured matrix. The data from the different shots are stacked column-wise. The pink dotted lines etched over the k-space data denote the odd lines of the k-space acquisition while the green dotted lines denote the even lines of the k-space acquisition. Structured low-rank matrix completion using H₁($\widehat{\mathbf{m}}$) can recover the missing k-space data for each shot.

(b) In the presence of odd-even shifts, the k-space data of each shot is separated into data coming from odd and even lines and stacked as a 3D matrix. The structured matrix H₂($\widehat{\mathbf{m}}$) is constructed as explained above and is used for matrix completion.

(c) Construction of the structured low-rank matrix H₃($\widehat{\mathbf{m}}$) to incorporate smoothness regularization. The k-space data is multiplied by −j2πk_x and −j2πk_y respectively. H₃($\widehat{\mathbf{m}}$) is constructed by the lifting of the resulting k-space data as shown.