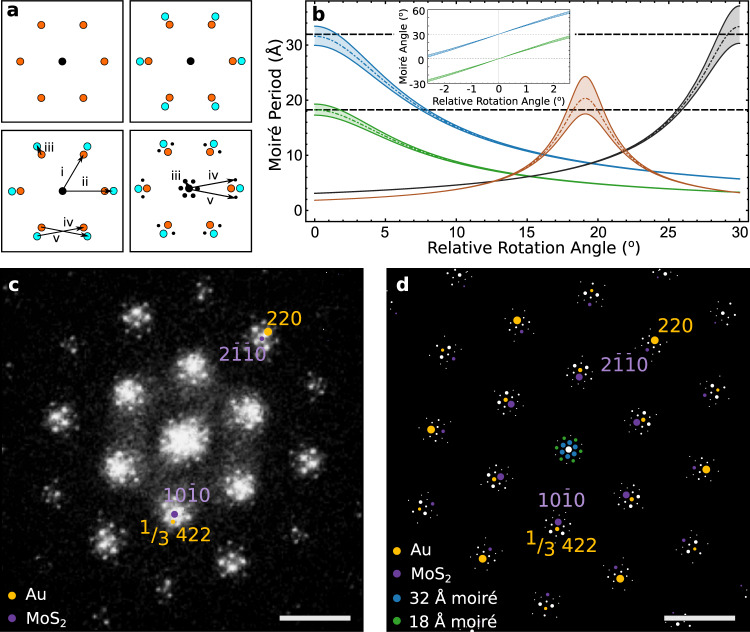
Fig. 3. Geometric convolution technique to predict moiré spectrum.

a Schematic representation of satellite spot generation. Spatial frequencies due to a single lattice shown in the top left panel (orange) are overlaid on those arising from a second lattice on the top right (cyan). The convolution of these two sets of spatial frequencies (i, ii) can be understood as the pairwise vectors connecting spatial frequencies of the two lattices (iii, iv, v - bottom, left). These convolutions generate moiré frequencies (iii, iv, v) shown as black dots in the bottom right panel. b Calculated moiré period vs rotation angle for the four largest moiré supercells in the MoS₂/Au{111} system, illustrated for small (±1%) Au lattice strain. Dot dashed lines represent 0% strain, while the two solid lines on either side represent ±1 strain as a bound. Black dashed lines represent the experimentally observed moiré periods from the FFT, two of which (18 Å and 32 Å) are predicted at 0° relative rotation angle. The moirés are color coded according to the reflections they arise from, with blue arising from the ${\left\{2\overline{11}0\right\}}_{{\mathrm{MoS}}_2}$: {220}_Au, green ${\left\{10\overline{1}0\right\}}_{{\mathrm{MoS}}_2}$:¹/₃{422}Au_, orange ${\left\{6\overline{33}0\right\}}_{{\mathrm{MoS}}_2}$: {642}_Au, and grey ${\left\{20\overline{2}0\right\}}_{{\mathrm{MoS}}_2}$: {220}_Au reflections, respectively. The inset shows the variation of moiré angle with relative rotation angle near 0°. c FFT of atomic resolution HRTEM image of the MoS₂/Au{111} image in Fig. 1c showing ¹/₃{422} reflection and two visible moiré periodicities around the central spot. Illustrative orange dots represent frequencies from Au crystal planes, while purple represent frequencies from MoS₂ crystal planes. Scale bar, 0.5 Å⁻¹. d Simulated FFT for Au/MoS₂ generated via the geometric convolution technique with each spot colored to show its origin (orange: Au, purple: MoS₂, blue: 32 Å crystallographic moiré, green: apparent 18 Å moiré). Area of spots is proportional to absolute intensity, but with inner moiré spots magnified 2x for clarity. Scale bar, 0.5 Å⁻¹.