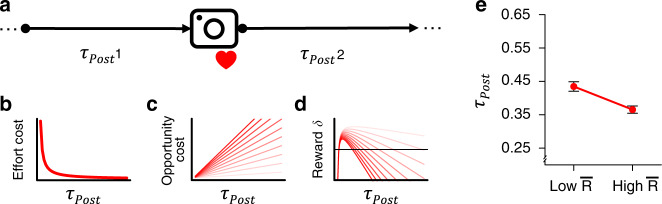
Fig. 1. Schematic illustration of the computational hypothesis.

a The $\overline{\mathrm{R}}\mathrm{L}$ model describes how τ_Post, the latency to the next social media post (denoted by the “camera” icon), is shaped by social rewards. Each post is followed by social reward (denoted by the “heart” symbol), which varies in number. The model adjusts the response policy, or threshold, which determines τ_Post, to maximize the average net rate of reward. b The $\overline{\mathrm{R}}\mathrm{L}$ model posits an effort cost to responding (e.g., taking pictures, uploading), which decreases as a function of τ_Post. The effort cost term penalizes posting in quick succession, because high effort reduces the average reward rate. c The opportunity cost of time increases as a function of the average reward rate $\overline{R}$. The gradient of red lines indicates increasing values of $\overline{R}$ (darker colors represent higher values), and thereby higher opportunity cost. d The optimal value of τ_Post, which maximizes the net reward δ, varies as function of $\overline{R}$ (darker colors represent higher values). The δ is used to update average reward rate $\overline{\mathrm{R}}$. Note that the optimum, indicated by the peak of the function, moves to shorter response latencies when $\overline{\mathrm{R}}$ is higher because the opportunity cost of time increases with $\overline{\mathrm{R}}$. The horizontal line denotes 0. The figure assumes a constant effort cost C. e Simulated model predictions. The $\overline{\mathrm{R}}\mathrm{L}$ model predicts that τ_Post, the latency between successive social media posts, will be shorter with high compared to low average reward rate, $\overline{\mathrm{R}}$. The simulation involved N = 1000 independent synthetic individuals. The prediction is presented as estimated mean ± 99% CI from mixed-effects regression.