Abstract
Machine learning techniques are widely used algorithms for predicting the mechanical properties of concrete. This study is based on the comparison of algorithms between individuals and ensemble approaches, such as bagging. Optimization for bagging is done by making 20 sub-models to depict the accurate one. Variables like cement content, fine and coarse aggregate, water, binder-to-water ratio, fly-ash, and superplasticizer are used for modeling. Model performance is evaluated by various statistical indicators like mean absolute error (MAE), mean square error (MSE), and root mean square error (RMSE). Individual algorithms show a moderate bias result. However, the ensemble model gives a better result with R2 = 0.911 compared to the decision tree (DT) and gene expression programming (GEP). K-fold cross-validation confirms the model’s accuracy and is done by R2, MAE, MSE, and RMSE. Statistical checks reveal that the decision tree with ensemble provides 25%, 121%, and 49% enhancement for errors like MAE, MSE, and RMSE between the target and outcome response.
Keywords: concrete compressive strength, fly ash waste, ensemble modeling, decision tree, DT-bagging regression, cross-validation python
1. Introduction
Carbon dioxide produced from the cement industry has a malignant adamant effect on environmental conditions [1]. Its utilization and excessive use in modern construction around the world produces greenhouse gases (GHG) [2]. Moreover, countless amounts of gases are emitted during the production of cement due to the burning of natural resources and fossil fuels [3]. Annually, 4 billion tons of Portland cement (PC) is being produced and approximately one ton of cement generates one ton of CO2 gas [4]. This huge amount of carbon dioxide is a serious threat to the environment. The report shows that a 1.6% increment (3.4% to 5%) of global CO2 gas discharge was observed from the year 2000 to 2006. The cement industry contributes 18% of industrial greenhouse gases (GHG to the environment. This is due to the direct process-related activity, energy-related combustion, and remaining use of electricity, which is termed as indirect energy [5]. To overcome the above-mentioned issue, a process of replacing the cement material with an alternative binder is of great research interest [6].
The supplementary cementation materials (SCMs) can be used for many purposes, especially in the concrete industry. Their utilization in concrete gives a benignant effect by reducing the percentage of CO2 gas emitted. SCMs used in the cement industry can be industrial and agricultural waste products, which includes olive oil, bagasse ash, sugarcane, rice husk ash, palm oil fuel ash, etc. However, commonly adopted and used in the construction industry are silica fume, fly ash, and ground granulated blast furnace slag [7,8,9]. Their utilization in concrete reduces the malignant effect on the environment [10]. The replacement of cement in concrete with the waste material helps both in the utilization of the wastes and fulfills the increasing demand for the concrete. What is more, it has been observed that the use of waste materials as pozzolanic in high-strength concrete improves its strength and durability. This alternately helps minimize the impending environmental degradation [11].
Concrete is stated as the second-highest used material after water in the world [12]. This is due to the intensive use of concrete in the construction industries and the field of civil engineering. Concrete requires a comprehensive technique to produce. It is a mixture of multiple materials like coarse aggregate, fine aggregate, water, binder, admixtures, and supplementary raw materials [13]. The concrete matrix is the random distribution of the previously mentioned variables [14]. The extensive use of it can be seen as a building material around the globe. For the effective evaluation of the performance of concrete according to the advanced design technologies, its mechanical properties must be examined [14]. One of its supreme mechanical properties is its compressive strength, which is alternately the sign of structural safety throughout life [15]. This remarkable property of concrete can be affected by numerous factors, like particle size, water-to-cement ratio, waste composition, and use of chemicals. However, casting concrete by using the proper techniques in the laboratory and conducting experimental tests to find the mechanical properties after the setting is quite a time-consuming task [14]. Moreover, using the previously mentioned technique in the recent and modern period of life is quite uneconomical. Thus, the modern methodologies of machine learning techniques can be adapted to predict the desired result in advance [16]. The prediction of variables can be done from regressions and machine learning models. These algorithm-based techniques give a precise relation and predict the accurate model by the use of input variables [17].
Machine learning approaches are raising trends in the domain of civil engineering. They are extensively used in forecasting the mechanical properties of concrete [18,19,20,21]. These techniques use extensive data to build a precise model. Their prediction accuracy is dependent upon the data sample used in experimental work during casting of the specimen or upon the literature study. Researchers use these algorithms for the prediction of the mechanical properties of concrete. Javed et al. [22] predict the compressive strength of sugarcane bagasse ash (SCBA) concrete using gene expression programming (GEP). The author used the experimental test for calibration and validation of the model. Similarly, Aslam et al. [23] predict the compressive strength of high-strength concrete (HSC) by employing GEP. The author used 357 data points and reported an adamant relationship between the target and predicted values. Hosein et al. [24] forecast the mechanical properties of recycled concrete (REC) by using an artificial neural network (ANN). Correspondingly, Getahun et al. [25] forecast the strength of concrete incorporating waste materials using ANN. The author concluded that ANN gives adamant relation with fewer errors. Similarly, Qing et al. [26] predict the diffusion capability of chloride in reinforced concrete structures with ANN. The result indicates better prediction by employing an individual algorithm based on 653 data samples. Farooq et al. [15] predict the compressive nature of HSC by developing two models with random forest (RF) and GEP. RF gives a robust performance with precise correlation with strong predicted values. That machine learning algorithm is not limited to predict only the compressive or tensile nature of concrete but can be used to forecast any response in any engineering or data sciences domain. In turn, Ahmad et al. [27] employ supervised machine learning (ML) algorithms to predict energy in the distinct buildings. Similarly, Wang et al. [28] predict the COVID-19 response by employing different ML-based algorithms. Cladera et al. [29] predict the response of a structural beam with and without stirrups by using ANN. The author achieved a better response from modeled than empirical relations. Similarly, Onyari et al. [30] reveal robust performance by utilizing ANN to predict the flexural and compressive strength of modified mortar. Previously mentioned examples show the overwhelming response of individual algorithms.
Recently, application of ensemble modeling is perceived as a chance for enhancement of the model’s overall efficiency. It can be achieved due to taking a weak leaner to build strong, predictive learners than individual learners [31]. Feng et al. [32] use ensemble algorithm techniques for the prediction of failure mode classification and bearing capacity of reinforced concrete (RC) structural element (column). Both models give robust performance. However, bearing capacity is characterized by better correlation than failure mode classification. Bui et al. [33] employed a modified firefly algorithm with ANN on high performance concrete (HPC) and reported better performance of the model. Moreover, Salamai et al. [34] report good accuracy of R2 = 0.9867 by using the RF algorithm. In turn, Cai et al. [35] use various supervised machine ensemble algorithms for the prediction of chloride penetration in the RC structure situated in a marine environment. Ensemble models outclass individual algorithms to predict chloride penetration in RC. Hacer et al. [36] present the comparative assessment of bagging as the ensemble approach for high-performance concrete mix slump flow. Ensemble models with bagging were found to be superior with regard to standalone approaches. Halil et al. [37] predict the strength of HPC by employing three ensemble modeling approaches. The author used the decision tree as a base learner for other models and found that the hybrid model outperforms with the output result of R2 = 0.9368 among the several proposed models. Kermani et al. [38] represents the performance of five soft, computing base learners for predicting concrete corrosion in sewers. The author used both tree-based and network-based learners and reported that RF ensemble learners give a better result with R2 = 0.872. These ensemble approaches give an enhanced effect with robust performance of the overall models.
Taking the above into consideration, it may seem that ensemble learning models have more favorable features and give better results than individual learning models. The difference between individual and ensemble model is illustrated in Figure 1.
Figure 1.
Comparison between individual and ensemble approaches.
2. Research Significance
The aim of this study is to use the machine-learning algorithm with ensemble modeling using Anaconda Python to predict the compressive strength of fly-ash-based concrete using different algorithms. A decision tree with a bagging algorithm is used and optimization is done by making 20 sub-models to give a strong outcome. A comparison is made with the individual, ensemble algorithms, and with gene expression programming to give the best model. Moreover, K-fold cross-validation and a statistical check are applied to evaluate the model performance.
3. Data Description
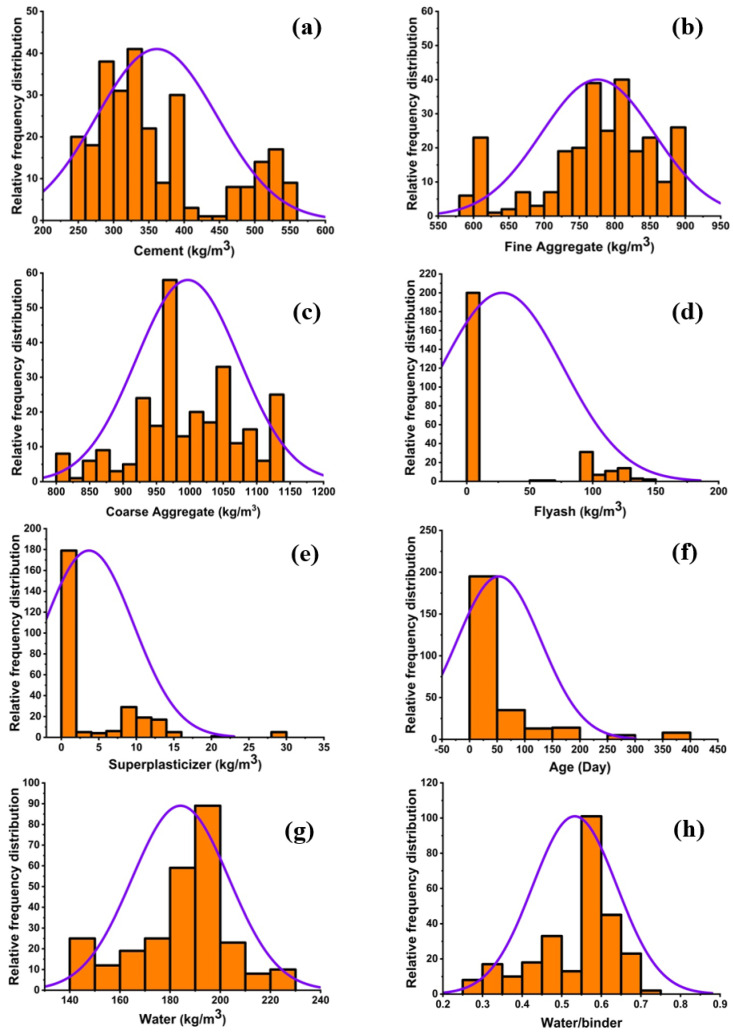
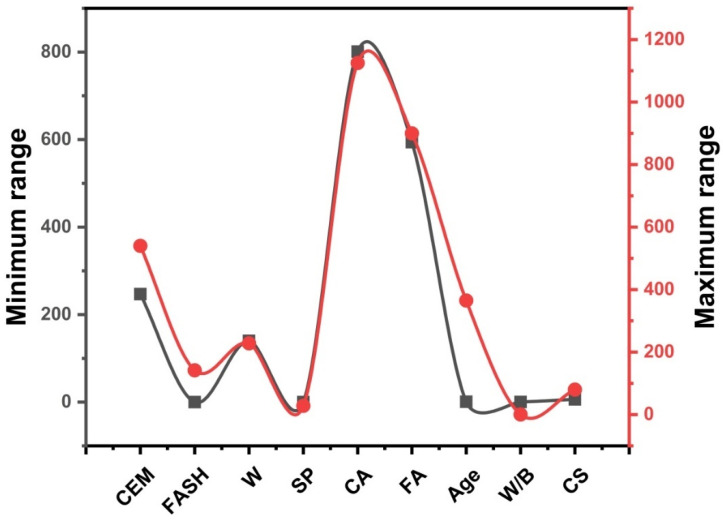
The efficiency of the model is completely dependent upon the variables and the number of data samples used. The parameters used in models preparation in order to predict the strength of concrete were taken from published literature [39] and are summarized in Appendix A. Eight variables concerning composition of the concrete mixture and including cement, fine and coarse aggregate, superplasticizer, water, waste material, age, and a water-to-binder ratio were taken into analysis. The overall distribution in terms of the relative frequency distribution is illustrated in Figure 2. The range of variables of each parameter used in the study, with a minimum and maximum value, is illustrated in Figure 3. Statistical descriptive analysis for the variables in terms of strength is listed in Table 1.
Figure 2.
Relative frequency distribution of variables, (a) cement, (b) fine aggregate, (c) coarse aggregate, (d) fly ash, (e) superplasticizer, (f) age, (g) water, and (h) water-to-binder ratio.
Figure 3.
Parameters range of variables with minimum and maximum values.
Table 1.
Statistical measures on variables.
| Statistics | Cem * | FASH * | W * | SP * | CA * | FA * | Age * | W/B * |
|---|---|---|---|---|---|---|---|---|
| Mean | 361.39 | 28.15 | 184.15 | 3.68 | 996.90 | 775.93 | 53.31 | 0.53 |
| Standard Error | 5.20 | 2.94 | 1.17 | 0.36 | 4.70 | 4.86 | 4.63 | 0.01 |
| Median | 336.25 | 0.00 | 189.00 | 0.00 | 987.80 | 781.95 | 28.00 | 0.58 |
| Mode | 349.00 | 0.00 | 192.00 | 0.00 | 1125.00 | 613.00 | 28.00 | 0.58 |
| Standard Deviation | 85.49 | 48.35 | 19.29 | 5.95 | 77.26 | 79.92 | 76.06 | 0.11 |
| Sample Variance | 7309.14 | 2337.79 | 372.16 | 35.39 | 5969.32 | 6387.59 | 5784.50 | 0.01 |
| Kurtosis | −0.50 | −0.44 | 0.29 | 3.52 | −0.19 | −0.07 | 7.01 | −0.04 |
| Skewness | 0.83 | 1.20 | −0.38 | 1.77 | −0.26 | −0.67 | 2.62 | −0.92 |
| Range | 293.20 | 142.00 | 88.00 | 28.20 | 324.00 | 305.80 | 364.00 | 0.43 |
| Minimum | 246.80 | 0.00 | 140.00 | 0.00 | 801.00 | 594.00 | 1.00 | 0.27 |
| Maximum | 540.00 | 142.00 | 228.00 | 28.20 | 1125.00 | 899.80 | 365.00 | 0.70 |
| Sum | 97,574.60 | 7601.70 | 49,720.30 | 993.40 | 269,163.90 | 209,502.40 | 14,394.00 | 143.89 |
| Count | 270.00 | 270.00 | 270.00 | 270.00 | 270.00 | 270.00 | 270.00 | 270.00 |
* CEM = Cement (kg/m3), FASH = Fly ash (kg/m3), W = Water (kg/m3), SP = Super plasticizer (kg/m3), CA = Coarse aggregate (kg/m3), FA = Fine aggregate (kg/m3), and W/B = Water to binder.
4. Methodology
Individual and ensemble model techniques used to predict the properties in a limited time that are of great interest. The accuracy level between the actual and prediction level is typically obtained from the R2 value (ranges from 0–0.99). A high R2 value indicates the satisfactory results of the selected technique. This study uses three approaches to predict the compressive strength of concrete with waste material. A decision tree with ensemble algorithms such as bagging with a learning rate of 0.9 and gene expression programming is used. These techniques are selected due to their popularity among other algorithms. The overall machine learning model methodology in the form of a diagram is illustrated in Figure 4.
Figure 4.
Machine learning model methodology.
4.1. Decision Tree
The decision tree is one of the supervised learning techniques used for categorizing regression problems but is also commonly used for classification problems [40]. There are classes inside the tree. However, if there is no class, then the regression technique can predict the outcome by independent variables [37]. A decision tree is a tree-structured classifier in which the inner nodes reflect the attribute of a database. Branches indicate the conclusion rules, and every leaf node constitutes the outcome. The decision tree consists of two nodes known as a decision node and a leaf node. Decision nodes have multiple branches with the capability to make any decision, while leaf nodes do not have branches and are considered as the output of the decisions. It is known as a decision tree because it has a similar nature to a tree that starts with the root node and distributes in the number of branches, and reflects a tree-like structure [41]. The decision tree splits the data samples at various points. The executed algorithm finds the error between the target and predicted value at every divided point. The errors are calculated at every divided point, and the variable with the least value for the fitness function is selected as a split point, and the same procedure is repeated again.
4.2. Ensemble Bagging Approach
The ensemble technique is the concept of machine learning used to train numerous models by applying a similar learning algorithm [42]. The ensemble involves a substantial group of methods known as multi-classifiers. The group of hundreds or thousands of learners with a common intent are joined together to fix the problem. Bagging is a parallel type ensemble method that explains the variance of the prediction model by producing supplementary data in the stage of training. This production is from irregular sampling including substituting from the real set of data. Some of the observations can be repeated by sampling with replacement in every new training data set. In bagging, every component has an equal chance to appear in the new dataset. The force of prediction cannot be enhanced by increasing the size of the training set. The variance can also be reduced narrowly by tuning the forecast to an anticipated outcome. All these numbers of sets of the given data are normally used to train other numbers of models. This ensemble of different models uses the average of all the predictions from the other various models. In regression, the prediction may be the mean or average of the predictions taken from the different models [43]. The decision tree with bagging is tuned with 20 sub-models to obtain the optimized value that gives an adamant output result.
4.3. Gene Expression Programming
Gene expression programming (GEP) is a computer programming-based algorithm used to develop different models [44]. GEP, which is initially introduced by Ferreira [45], is considered to be a natural development of genetic programming (GP). Multiple numbers of genetic operators that are being used in genetic algorithms (GAs) can also be used in GEP with the help of a few recommended changes. There are five main components of GEP, namely, function set, terminal set, fitness function, control variables, and termination condition. GEP works as a fixed length of character twine to explain the problems, which are next defined as tree-like structures with different dimensions. This type of tree is known as the GEP expression tree (ETs). Selection of individual chromosomes takes place and then they are copied into the next generation, as per the fitness by roulette wheel sampling with elitism [23]. This ensures the durability and replication of the best individual to the next generation. Fluctuation in the population is shown by applying one or more genetic operators (mutation, crossover, or rotation) on the given chromosomes. Among the number of advantages of GEP, the formation of genetic diversity is remarkably simplified because of the working of genetic operators at the chromosome level. This multi-genic approach of GEP permits the natural selection of other complicated and complex programs composed of numerous subprograms. GEP genes along with a function set and terminal set play a vital role during the process [46].
4.4. K-Fold Cross-Validation and Statistical Measures
The model performance in terms of bias and variance is checked by employing K-fold cross-validation. The data is divided into 10 stratified groups, which randomly distribute the data into a training set and test set. This process takes one part of the overall data into the test sample and the remaining into the training set, as illustrated in Figure 5. The model’s overall efficiency by cross-validation is then tested by taking an average of 10 rounds by various errors. Similarly, the model evaluation is also done by using statistical indicators [23]. Three types of the indicator are used in our current study, which is listed below (Equations (1)–(3)).
| (1) |
| (2) |
| (3) |
where:
n = Total number of data samples,
= reference values in the data sample,
= predicted values from models.
Figure 5.
K-fold cross-validation algorithm [46].
5. Model Result
5.1. Decision Tree/Ensemble Model
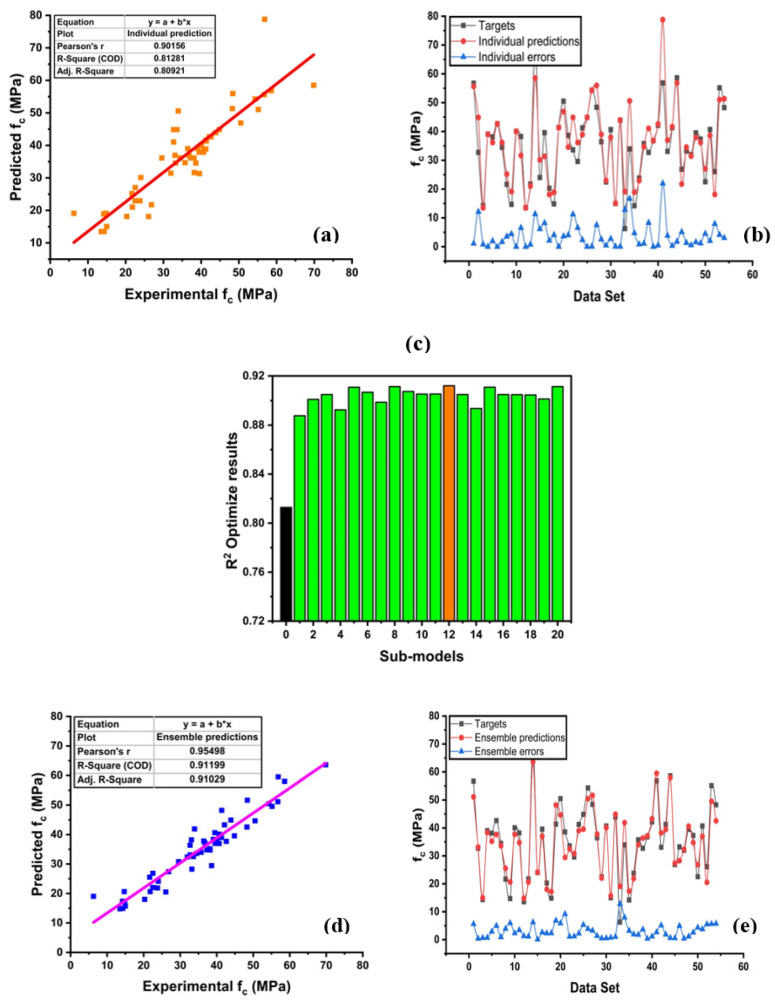
The prediction of concrete strength by employing a decision tree yields an adamantly strong relationship between targets to output strength, as depicted in Figure 6. It can be seen that the individual model gives a better response with less variance, as illustrated in Figure 6a. However, the decision tree with bagging gives precise performance than an individual one, as illustrated in Figure 6d. This is due to an increase in model efficiency as it takes several data to train the best model by using weak base learners [47]. The ensemble model is optimized by making 20 sub-models, as depicted in Figure 6c. The zero number shows the individual model, which is made by using the decision approach and shows R2 = 0.812. After the ensemble approach, there is a significant enhancement in the overall response of the model. Every model shows a surpass effect by giving an average score of about R2 = 0.904 within 20 models. However, the 12th sub-model gives a prime result with R2 = 0.911, as depicted in Figure 6c. Moreover, the model comparison in terms of errors is depicted in Figure 6b,e. Decision tree (DT) with bagging enhances the model accuracy by giving fewer errors. The test data shows that there is a 20.10% prediction capacity of average errors by bagging than in the individual model. Besides, DT shows the minimum and maximum error of 0 and 21.97 MPa, respectively. Similarly, DT with an ensemble model shows the minimum and maximum error of 0.11, and 12.77 MPa, respectively. The detailed result is shown in Table 2.
Figure 6.
Decision tree (DT) with the ensemble model. (a) Predicted regression model with DT. (b) Model errors between targets and predictions from the DT technique. (c) Optimize model of ensemble. (d) Predicted regression model with DT-bagging. (e) Model Errors between targets and predictions from the DT-bagging technique.
Table 2.
Evaluation of models.
| Data Points | Decision Tree (DT) Targets | DT Predictions | Ensemble Prediction | Gene Expression Programming (GEP) Targets | GEP Predictions | DT Errors | Ensemble Errors | GEP Errors |
|---|---|---|---|---|---|---|---|---|
| 1 | 56.74 | 55.64 | 51.14 | 26.74 | 27.66 | 1.10 | 5.60 | 0.92 |
| 2 | 32.72 | 44.87 | 33.11 | 37.44 | 37.21 | 12.15 | 0.39 | 0.23 |
| 3 | 14.31 | 13.52 | 14.94 | 51.04 | 49.48 | 0.79 | 0.63 | 1.56 |
| 4 | 39.06 | 39.05 | 38.35 | 18.13 | 21.68 | 0.01 | 0.71 | 3.55 |
| 5 | 38.11 | 36.15 | 35.22 | 51.33 | 49.31 | 1.96 | 2.89 | 2.02 |
| 6 | 42.64 | 42.64 | 37.67 | 37.91 | 39.76 | 0.00 | 4.97 | 1.85 |
| 7 | 34.49 | 36.15 | 33.57 | 25.10 | 36.42 | 1.66 | 0.92 | 11.32 |
| 8 | 21.65 | 25.18 | 25.55 | 74.17 | 77.61 | 3.53 | 3.90 | 3.44 |
| 9 | 14.7 | 19.11 | 20.62 | 37.27 | 40.69 | 4.41 | 5.92 | 3.42 |
| 10 | 40.06 | 40.06 | 37.74 | 15.05 | 14.58 | 0.00 | 2.32 | 0.47 |
| 11 | 38.21 | 31.65 | 34.74 | 23.52 | 22.76 | 6.56 | 3.47 | 0.76 |
| 12 | 13.52 | 13.52 | 14.79 | 41.89 | 42.56 | 0.00 | 1.27 | 0.67 |
| 13 | 21.78 | 21.02 | 20.63 | 48.79 | 46.44 | 0.76 | 1.15 | 2.35 |
| 14 | 69.84 | 58.52 | 63.61 | 40.68 | 40.59 | 11.32 | 6.23 | 0.09 |
| 15 | 24 | 30.14 | 24.11 | 32.92 | 34.99 | 6.14 | 0.11 | 2.07 |
| 16 | 39.58 | 31.35 | 37.01 | 25.18 | 26.87 | 8.23 | 2.57 | 1.69 |
| 17 | 20.28 | 18.13 | 18.00 | 59.20 | 85.40 | 2.15 | 2.28 | 26.20 |
| 18 | 14.84 | 18.91 | 17.15 | 33.94 | 32.67 | 4.07 | 2.31 | 1.27 |
| 19 | 41.37 | 41.37 | 48.22 | 53.30 | 49.35 | 0.00 | 6.85 | 3.95 |
| 20 | 50.51 | 46.9 | 44.65 | 42.22 | 46.77 | 3.61 | 5.86 | 4.55 |
| 21 | 38.6 | 34.57 | 29.43 | 30.96 | 18.90 | 4.03 | 9.17 | 12.06 |
| 22 | 33.61 | 44.87 | 32.51 | 21.75 | 25.93 | 11.26 | 1.10 | 4.18 |
| 23 | 29.59 | 36.15 | 30.80 | 12.54 | 9.95 | 6.56 | 1.21 | 2.59 |
| 24 | 41.24 | 38.89 | 39.02 | 31.18 | 37.50 | 2.35 | 2.22 | 6.32 |
| 25 | 44.86 | 44.87 | 39.55 | 14.20 | 16.26 | 0.01 | 5.31 | 2.06 |
| 26 | 54.32 | 54.28 | 50.46 | 33.80 | 36.88 | 0.04 | 3.86 | 3.08 |
| 27 | 48.4 | 55.94 | 51.65 | 30.14 | 29.77 | 7.54 | 3.25 | 0.37 |
| 28 | 36.45 | 39 | 37.80 | 31.88 | 36.23 | 2.55 | 1.35 | 4.35 |
| 29 | 22.5 | 22.95 | 22.03 | 30.12 | 36.52 | 0.45 | 0.47 | 6.40 |
| 30 | 40.66 | 37.91 | 40.12 | 32.72 | 32.57 | 2.75 | 0.54 | 0.15 |
| 31 | 14.99 | 15.05 | 15.71 | 30.85 | 41.47 | 0.06 | 0.72 | 10.62 |
| 32 | 43.89 | 43.94 | 44.89 | 43.70 | 45.88 | 0.05 | 1.00 | 2.18 |
| 33 | 6.27 | 19.11 | 19.05 | 24.50 | 25.95 | 12.84 | 12.78 | 1.45 |
| 34 | 33.94 | 50.6 | 41.89 | 39.29 | 41.35 | 16.66 | 7.95 | 2.06 |
| 35 | 14.2 | 18.91 | 17.38 | 32.07 | 35.21 | 4.71 | 3.18 | 3.14 |
| 36 | 23.8 | 22.95 | 21.86 | 9.01 | 13.37 | 0.85 | 1.94 | 4.36 |
| 37 | 35.76 | 34.68 | 33.99 | 22.50 | 18.93 | 1.08 | 1.77 | 3.57 |
| 38 | 32.72 | 41.05 | 36.38 | 14.50 | 16.89 | 8.33 | 3.66 | 2.39 |
| 39 | 36.8 | 36.8 | 37.17 | 39.06 | 37.75 | 0.00 | 0.37 | 1.31 |
| 40 | 42.13 | 42.62 | 43.28 | 42.42 | 43.95 | 0.49 | 1.15 | 1.53 |
| 41 | 56.83 | 78.8 | 59.50 | 42.13 | 38.72 | 21.97 | 2.67 | 3.41 |
| 42 | 33.08 | 36.94 | 38.20 | 42.03 | 48.82 | 3.86 | 5.12 | 6.79 |
| 43 | 41.3 | 41.64 | 39.45 | 43.89 | 46.77 | 0.34 | 1.85 | 2.88 |
| 44 | 58.61 | 56.85 | 58.01 | 40.06 | 31.79 | 1.76 | 0.60 | 8.27 |
| 45 | 26.85 | 21.75 | 27.39 | 48.28 | 47.22 | 5.10 | 0.54 | 1.06 |
| 46 | 33.21 | 34.57 | 28.27 | 37.42 | 37.11 | 1.36 | 4.94 | 0.31 |
| 47 | 31.97 | 31.45 | 32.39 | 39.49 | 41.69 | 0.52 | 0.42 | 2.20 |
| 48 | 39.49 | 37.91 | 40.61 | 36.94 | 38.73 | 1.58 | 1.12 | 1.79 |
| 49 | 37.33 | 36.15 | 34.77 | 25.22 | 27.85 | 1.18 | 2.56 | 2.63 |
| 50 | 22.53 | 27.04 | 26.86 | 55.64 | 55.64 | 4.51 | 4.33 | 0.00 |
| 51 | 40.68 | 38.63 | 36.96 | 60.95 | 60.16 | 2.05 | 3.72 | 0.79 |
| 52 | 26.06 | 18.13 | 20.51 | 37.33 | 40.76 | 7.93 | 5.55 | 3.43 |
| 53 | 55.16 | 51.04 | 49.54 | 25.45 | 29.65 | 4.12 | 5.62 | 4.20 |
| 54 | 48.28 | 51.33 | 42.55 | - | - | 3.05 | 5.73 | - |
5.2. Gene Expression Programming
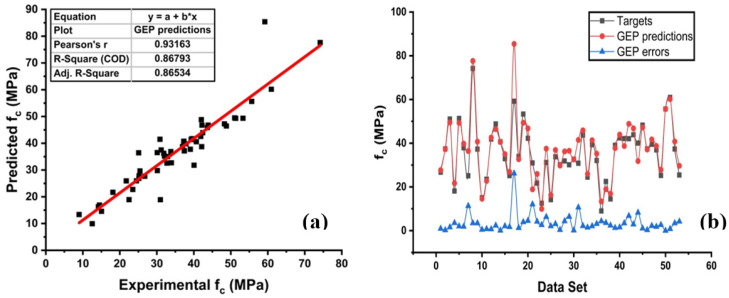
The performance of the model by GEP yielded a robust relationship between targets and predicted, as illustrated in Figure 7. It can be seen that R2 by employing GEP is close to 1. Moreover, Figure 7b represents the error distribution of the testing set with fewer errors. Similarly, the predicted value shows a lower error to target values with a minimum, maximum, and average value of 0.00 MPa, 26.20 MPa, and 3.48 MPa, respectively. Table 2 presents detailed results from the models.
Figure 7.
Gene expression programming (GEP) model: (a) Predicted regression model. (b) Model Errors between targets and predictions from the GEP model.
5.3. Evaluation of the Model by K-Fold and Statistical Checks
Cross-validation is a statistical practice used to evaluate or estimate the actual performance of the machine learning models. It is necessary to know the performance of the selected models. For this purpose, a validation technique is required to find the accuracy level of the model’s data. Shuffling of the data set randomly and splitting a dataset into k-groups is required for the k-fold validation test. In the described study, data of experimental samples are equally divided into 10 subsets. It uses nine out of ten subsets, while the only subset is utilized for the validation of the model. The same approach of this process is then repeated 10 times for obtaining the average accuracy of these 10 repetitions. It is clarified widely that the 10-fold cross-validation method well represents the conclusion and accuracy of the model performance [48].
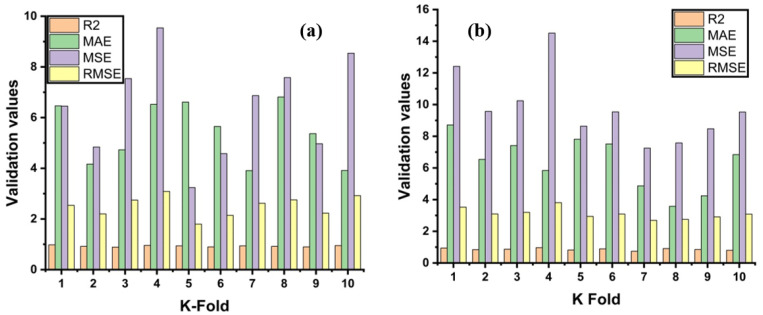
Bias and a variance decrease for the test set can be checked by employing K-fold cross-validation. The results of cross-validation are evaluated by a correlation coefficient (R2), a mean absolute error (MAE), a mean square error (MSE), and a root mean square error (RMSE), as illustrated in Figure 8. The ensemble model shows fewer errors and better R2 as compared to GEP. The average R2 for ensemble modeling is 0.905 with a maximum and minimum values of 0.84 and 0.96, as depicted in Figure 8a. Whereas the GEP model shows an average R2 = 0.873 of ten folds with 0.76 and 0.95 for a minimum and maximum correlation, respectively, as shown in Figure 8b. Each model shows fewer errors for validation. The validation indicator result shows that ensemble means values of MAE, MSE, and RMSE come to be 6.43 MPa, 6.66 MPa, and 2.55 MPa, respectively. Similarly, the GEP model shows the same trend by showing fewer errors. The GEP model shows mean values of 7.30 MPa, 9.60 MPa, and 3.06 MPa for MAE, MSE, and RMSE, respectively (see Figure 8b). Table 3 represents the validation results of both models.
Figure 8.
Statistical indicators from K-Fold Cross-validation; (a) Ensemble model; (b) GEP model.
Table 3.
Result of K-Fold Cross-validation.
| K Fold | Ensemble Model | GEP Model | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | MAE | MSE | RMSE | R2 | MAE | MSE | RMSE | |
| 1 | 0.96 | 8.46 | 4.45 | 2.10 | 0.86 | 10.71 | 13.57 | 3.68 |
| 2 | 0.91 | 5.17 | 7.44 | 2.72 | 0.94 | 7.45 | 7.97 | 2.82 |
| 3 | 0.84 | 3.73 | 8.54 | 2.92 | 0.89 | 6.18 | 11.24 | 3.35 |
| 4 | 0.90 | 9.52 | 5.84 | 2.41 | 0.95 | 5.84 | 14.51 | 3.80 |
| 5 | 0.94 | 6.81 | 6.44 | 2.53 | 0.93 | 7.81 | 9.64 | 3.10 |
| 6 | 0.90 | 5.65 | 5.88 | 2.42 | 0.86 | 7.51 | 6.51 | 2.55 |
| 7 | 0.85 | 7.91 | 6.87 | 2.62 | 0.81 | 8.47 | 7.25 | 2.69 |
| 8 | 0.88 | 5.81 | 9.85 | 3.13 | 0.76 | 6.58 | 7.58 | 2.75 |
| 9 | 0.95 | 6.37 | 4.97 | 2.22 | 0.84 | 5.64 | 9.47 | 3.07 |
| 10 | 0.92 | 4.92 | 6.35 | 2.51 | 0.89 | 6.84 | 8.35 | 2.88 |
Statistical check is also applied to evaluate the model with regard to the testing results. The statistical check is an indicator that shows the model response towards prediction, as shown in Table 4. It can be seen that models depict bottom-most errors. However, the ensemble model shows a 25% error reduction for MAE as compared to the individual and GEP. Similarly, the bagging approach indicates the robust performance of the model. Moreover, MSE and RMSE for strong learners show 121% and 49% enhancement in the predictions by showing reduced errors between the target and predicted outcomes, as shown in Table 4.
Table 4.
Statistical checks.
| Statistics | MAE (MPa) | MSE (MPa) | RMSE (MPa) |
|---|---|---|---|
| DT | 3.896 | 36.01 | 6.00 |
| DT-BAG | 3.113 | 16.28 | 4.03 |
| GEP | 3.478 | 29.91 | 5.46 |
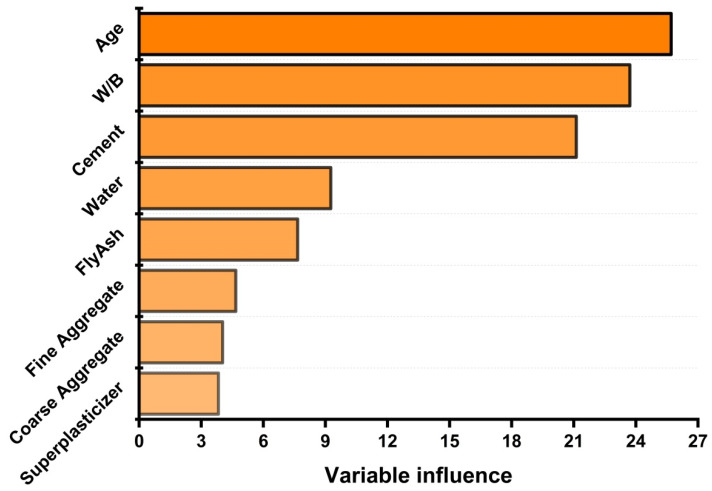
Moreover, permutation feature importance via python is conducted to check the influence of variables on strength, as depicted in Figure 9. These variables have a vital influence on the prediction of compressive strength of concrete. The concrete age, cement, and water-to-cement ratio have a significant influence on model analysis. Whereas water, filler material (fly ash), superplasticizer, fine aggregate, and coarse aggregate have moderate influences in making the model. Thus, it can be concluded that every parameter is crucial in the forecasting of the strength properties. However, cement, age, and the water-to-cement ratio should be given more importance while casting of specimens.
Figure 9.
Variable influence on compressive strength of fly ash-based concrete.
5.4. Limitation and Future Work
Despite the fact that, in the work, a thorough analysis based on a large number of data points was conducted and an extensive machine learning algorithm with evaluation was implemented, the limitations of work should be mentioned. Described in the paper selection, an approach can be enhanced by using other appropriate methods. A clear limitation of work is the number of data points equal to 270. The study is also limited to predict only one result from various mechanical properties of concrete. Tensile strength, durability, corrosion, toughness, and abrasion behavior of concrete is not considered in this work. Other algorithm-based techniques, like artificial neural network (ANN), support vector machine (SVM), gradient boosting, and AdaBoost may also be applied to the same dataset for a better understanding. However, this research work does not only focus on algorithm-based techniques but also involves the programming-based GEP, which indicated the wide scope of this work.
Since concrete is the most widely used material after water on this earth, it is further recommended that other properties of this material should be incorporated except for its compressive strength. Machine learning techniques should also be used to predict the environmental effects on concrete properties. To achieve high accuracy in the actual and predicted results, the multi-stage genetic programming approach may also be used. It is also recommended that models can be run for the concrete modified with different fibers as: jute fibers, glass fibers, polypropylene fibers, nylon fibers, and steel fibers.
6. Conclusions
This study describes the supervised machine learning approaches with ensemble modeling and gene expression programming to predict concrete strength. The following points are drawn from the analysis:
A decision tree with ensemble modeling gives a robust performance compared to a decision tree individually and with gene expression programming. The correlation coefficient of R2 = 0.911 is reported for DT with bagging.
Optimization of the model for the decision tree with bagging is done by making twenty sub-models. Magnificent enhancement is observed from the twelve, which shows R2 = 0.911 as compared to the individual model with R2 = 0.812.
Validation score is conducted by different indicators. Both models (DT with bagging and GEP) show better anticipation for testing results.
Statistical analysis checks reveal that the decision tree with bagging shows enhancement in model accuracy by minimizing the error difference between targeted and predicted values.
To summarize, all applied algorithms show a significant effect on the model’s quality by predicting the target response more accurately. As described in the paper, machine learning approaches can save experimental time and predict the outcome by gathering extensive data from laboratory and published papers. It can help the scientific society to predict the properties and responses in the coming month or year.
Appendix A
Table A1.
Experimental variable data.
| S. No. | Cement | Fly Ash | Water | Super Plasticizer | Coarse Aggregate | Fine Aggregate | Days | W/C | Strength |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 540 | 0 | 162 | 2.5 | 1040 | 676 | 28 | 0.3 | 79.99 |
| 2 | 540 | 0 | 162 | 2.5 | 1055 | 676 | 28 | 0.3 | 61.89 |
| 3 | 475 | 0 | 228 | 0 | 932 | 594 | 28 | 0.48 | 39.29 |
| 4 | 380 | 0 | 228 | 0 | 932 | 670 | 90 | 0.6 | 52.91 |
| 5 | 475 | 0 | 228 | 0 | 932 | 594 | 180 | 0.48 | 42.62 |
| 6 | 380 | 0 | 228 | 0 | 932 | 670 | 365 | 0.6 | 52.52 |
| 7 | 380 | 0 | 228 | 0 | 932 | 670 | 270 | 0.6 | 53.3 |
| 8 | 475 | 0 | 228 | 0 | 932 | 594 | 7 | 0.48 | 38.6 |
| 9 | 475 | 0 | 228 | 0 | 932 | 594 | 270 | 0.48 | 42.13 |
| 10 | 475 | 0 | 228 | 0 | 932 | 594 | 90 | 0.48 | 42.23 |
| 11 | 380 | 0 | 228 | 0 | 932 | 670 | 180 | 0.6 | 53.1 |
| 12 | 349 | 0 | 192 | 0 | 1047 | 806.9 | 3 | 0.55 | 15.05 |
| 13 | 475 | 0 | 228 | 0 | 932 | 594 | 365 | 0.48 | 41.93 |
| 14 | 310 | 0 | 192 | 0 | 971 | 850.6 | 3 | 0.62 | 9.87 |
| 15 | 485 | 0 | 146 | 0 | 1120 | 800 | 28 | 0.3 | 71.99 |
| 16 | 531.3 | 0 | 141.8 | 28.2 | 852.1 | 893.7 | 3 | 0.27 | 41.3 |
| 17 | 531.3 | 0 | 141.8 | 28.2 | 852.1 | 893.7 | 7 | 0.27 | 46.9 |
| 18 | 531.3 | 0 | 141.8 | 28.2 | 852.1 | 893.7 | 28 | 0.27 | 56.4 |
| 19 | 531.3 | 0 | 141.8 | 28.2 | 852.1 | 893.7 | 56 | 0.27 | 58.8 |
| 20 | 531.3 | 0 | 141.8 | 28.2 | 852.1 | 893.7 | 91 | 0.27 | 59.2 |
| 21 | 290.4 | 96.2 | 168.1 | 9.4 | 961.2 | 865 | 3 | 0.58 | 22.5 |
| 22 | 290.4 | 96.2 | 168.1 | 9.4 | 961.2 | 865 | 14 | 0.58 | 34.67 |
| 23 | 290.4 | 96.2 | 168.1 | 9.4 | 961.2 | 865 | 28 | 0.58 | 34.74 |
| 24 | 290.4 | 96.2 | 168.1 | 9.4 | 961.2 | 865 | 56 | 0.58 | 45.08 |
| 25 | 290.4 | 96.2 | 168.1 | 9.4 | 961.2 | 865 | 100 | 0.58 | 48.97 |
| 26 | 277.1 | 97.4 | 160.6 | 11.8 | 973.9 | 875.6 | 3 | 0.58 | 23.14 |
| 27 | 277.1 | 97.4 | 160.6 | 11.8 | 973.9 | 875.6 | 14 | 0.58 | 41.89 |
| 28 | 277.1 | 97.4 | 160.6 | 11.8 | 973.9 | 875.6 | 28 | 0.58 | 48.28 |
| 29 | 277.1 | 97.4 | 160.6 | 11.8 | 973.9 | 875.6 | 56 | 0.58 | 51.04 |
| 30 | 277.1 | 97.4 | 160.6 | 11.8 | 973.9 | 875.6 | 100 | 0.58 | 55.64 |
| 31 | 295.7 | 95.6 | 171.5 | 8.9 | 955.1 | 859.2 | 3 | 0.58 | 22.95 |
| 32 | 295.7 | 95.6 | 171.5 | 8.9 | 955.1 | 859.2 | 14 | 0.58 | 35.23 |
| 33 | 295.7 | 95.6 | 171.5 | 8.9 | 955.1 | 859.2 | 28 | 0.58 | 39.94 |
| 34 | 295.7 | 95.6 | 171.5 | 8.9 | 955.1 | 859.2 | 56 | 0.58 | 48.72 |
| 35 | 295.7 | 95.6 | 171.5 | 8.9 | 955.1 | 859.2 | 100 | 0.58 | 52.04 |
| 36 | 251.8 | 99.9 | 146.1 | 12.4 | 1006 | 899.8 | 3 | 0.58 | 21.02 |
| 37 | 251.8 | 99.9 | 146.1 | 12.4 | 1006 | 899.8 | 14 | 0.58 | 33.36 |
| 38 | 251.8 | 99.9 | 146.1 | 12.4 | 1006 | 899.8 | 28 | 0.58 | 33.94 |
| 39 | 251.8 | 99.9 | 146.1 | 12.4 | 1006 | 899.8 | 56 | 0.58 | 44.14 |
| 40 | 251.8 | 99.9 | 146.1 | 12.4 | 1006 | 899.8 | 100 | 0.58 | 45.37 |
| 41 | 249.1 | 98.8 | 158.1 | 12.8 | 987.8 | 889 | 3 | 0.63 | 15.36 |
| 42 | 249.1 | 98.8 | 158.1 | 12.8 | 987.8 | 889 | 14 | 0.63 | 28.68 |
| 43 | 249.1 | 98.8 | 158.1 | 12.8 | 987.8 | 889 | 28 | 0.63 | 30.85 |
| 44 | 249.1 | 98.8 | 158.1 | 12.8 | 987.8 | 889 | 56 | 0.63 | 42.03 |
| 45 | 249.1 | 98.8 | 158.1 | 12.8 | 987.8 | 889 | 100 | 0.63 | 51.06 |
| 46 | 252.3 | 98.8 | 146.3 | 14.2 | 987.8 | 889 | 3 | 0.58 | 21.78 |
| 47 | 252.3 | 98.8 | 146.3 | 14.2 | 987.8 | 889 | 14 | 0.58 | 42.29 |
| 48 | 252.3 | 98.8 | 146.3 | 14.2 | 987.8 | 889 | 28 | 0.58 | 50.6 |
| 49 | 252.3 | 98.8 | 146.3 | 14.2 | 987.8 | 889 | 56 | 0.58 | 55.83 |
| 50 | 252.3 | 98.8 | 146.3 | 14.2 | 987.8 | 889 | 100 | 0.58 | 60.95 |
| 51 | 246.8 | 125.1 | 143.3 | 12 | 1086.8 | 800.9 | 3 | 0.58 | 23.52 |
| 52 | 246.8 | 125.1 | 143.3 | 12 | 1086.8 | 800.9 | 14 | 0.58 | 42.22 |
| 53 | 246.8 | 125.1 | 143.3 | 12 | 1086.8 | 800.9 | 28 | 0.58 | 52.5 |
| 54 | 246.8 | 125.1 | 143.3 | 12 | 1086.8 | 800.9 | 56 | 0.58 | 60.32 |
| 55 | 246.8 | 125.1 | 143.3 | 12 | 1086.8 | 800.9 | 100 | 0.58 | 66.42 |
| 56 | 275.1 | 121.4 | 159.5 | 9.9 | 1053.6 | 777.5 | 3 | 0.58 | 23.8 |
| 57 | 275.1 | 121.4 | 159.5 | 9.9 | 1053.6 | 777.5 | 14 | 0.58 | 38.77 |
| 58 | 275.1 | 121.4 | 159.5 | 9.9 | 1053.6 | 777.5 | 28 | 0.58 | 51.33 |
| 59 | 275.1 | 121.4 | 159.5 | 9.9 | 1053.6 | 777.5 | 56 | 0.58 | 56.85 |
| 60 | 275.1 | 121.4 | 159.5 | 9.9 | 1053.6 | 777.5 | 100 | 0.58 | 58.61 |
| 61 | 297.2 | 117.5 | 174.8 | 9.5 | 1022.8 | 753.5 | 3 | 0.59 | 21.91 |
| 62 | 297.2 | 117.5 | 174.8 | 9.5 | 1022.8 | 753.5 | 14 | 0.59 | 36.99 |
| 63 | 297.2 | 117.5 | 174.8 | 9.5 | 1022.8 | 753.5 | 28 | 0.59 | 47.4 |
| 64 | 297.2 | 117.5 | 174.8 | 9.5 | 1022.8 | 753.5 | 56 | 0.59 | 51.96 |
| 65 | 297.2 | 117.5 | 174.8 | 9.5 | 1022.8 | 753.5 | 100 | 0.59 | 56.74 |
| 66 | 376 | 0 | 214.6 | 0 | 1003.5 | 762.4 | 3 | 0.57 | 16.28 |
| 67 | 376 | 0 | 214.6 | 0 | 1003.5 | 762.4 | 14 | 0.57 | 25.62 |
| 68 | 376 | 0 | 214.6 | 0 | 1003.5 | 762.4 | 28 | 0.57 | 31.97 |
| 69 | 376 | 0 | 214.6 | 0 | 1003.5 | 762.4 | 56 | 0.57 | 36.3 |
| 70 | 376 | 0 | 214.6 | 0 | 1003.5 | 762.4 | 100 | 0.57 | 43.06 |
| 71 | 500 | 0 | 140 | 4 | 966 | 853 | 28 | 0.28 | 67.57 |
| 72 | 475 | 59 | 142 | 1.9 | 1098 | 641 | 28 | 0.3 | 57.23 |
| 73 | 505 | 60 | 195 | 0 | 1030 | 630 | 28 | 0.39 | 64.02 |
| 74 | 451 | 0 | 165 | 11.3 | 1030 | 745 | 28 | 0.37 | 78.8 |
| 75 | 516 | 0 | 162 | 8.2 | 801 | 802 | 28 | 0.31 | 41.37 |
| 76 | 520 | 0 | 170 | 5.2 | 855 | 855 | 28 | 0.33 | 60.28 |
| 77 | 528 | 0 | 185 | 6.9 | 920 | 720 | 28 | 0.35 | 56.83 |
| 78 | 520 | 0 | 175 | 5.2 | 870 | 805 | 28 | 0.34 | 51.02 |
| 79 | 385 | 136 | 158 | 20 | 903 | 768 | 28 | 0.41 | 55.55 |
| 80 | 500.1 | 0 | 200 | 3 | 1124.4 | 613.2 | 28 | 0.4 | 44.13 |
| 81 | 405 | 0 | 175 | 0 | 1120 | 695 | 28 | 0.43 | 52.3 |
| 82 | 516 | 0 | 162 | 8.3 | 801 | 802 | 28 | 0.31 | 41.37 |
| 83 | 475 | 0 | 162 | 9.5 | 1044 | 662 | 28 | 0.34 | 58.52 |
| 84 | 500 | 0 | 151 | 9 | 1033 | 655 | 28 | 0.3 | 69.84 |
| 85 | 436 | 0 | 218 | 0 | 838.4 | 719.7 | 28 | 0.5 | 23.85 |
| 86 | 289 | 0 | 192 | 0 | 913.2 | 895.3 | 90 | 0.66 | 32.07 |
| 87 | 289 | 0 | 192 | 0 | 913.2 | 895.3 | 3 | 0.66 | 11.65 |
| 88 | 393 | 0 | 192 | 0 | 940.6 | 785.6 | 3 | 0.49 | 19.2 |
| 89 | 393 | 0 | 192 | 0 | 940.6 | 785.6 | 90 | 0.49 | 48.85 |
| 90 | 393 | 0 | 192 | 0 | 940.6 | 785.6 | 28 | 0.49 | 39.6 |
| 91 | 480 | 0 | 192 | 0 | 936.2 | 712.2 | 28 | 0.4 | 43.94 |
| 92 | 480 | 0 | 192 | 0 | 936.2 | 712.2 | 7 | 0.4 | 34.57 |
| 93 | 480 | 0 | 192 | 0 | 936.2 | 712.2 | 90 | 0.4 | 54.32 |
| 94 | 480 | 0 | 192 | 0 | 936.2 | 712.2 | 3 | 0.4 | 24.4 |
| 95 | 333 | 0 | 192 | 0 | 931.2 | 842.6 | 3 | 0.58 | 15.62 |
| 96 | 289 | 0 | 192 | 0 | 913.2 | 895.3 | 7 | 0.66 | 14.6 |
| 97 | 333 | 0 | 192 | 0 | 931.2 | 842.6 | 28 | 0.58 | 31.97 |
| 98 | 333 | 0 | 192 | 0 | 931.2 | 842.6 | 7 | 0.58 | 23.4 |
| 99 | 289 | 0 | 192 | 0 | 913.2 | 895.3 | 28 | 0.66 | 25.57 |
| 100 | 333 | 0 | 192 | 0 | 931.2 | 842.6 | 90 | 0.58 | 41.68 |
| 101 | 393 | 0 | 192 | 0 | 940.6 | 785.6 | 7 | 0.49 | 27.74 |
| 102 | 397 | 0 | 185.7 | 0 | 1040.6 | 734.3 | 28 | 0.47 | 33.08 |
| 103 | 382.5 | 0 | 185.7 | 0 | 1047.8 | 739.3 | 7 | 0.49 | 24.07 |
| 104 | 295.8 | 0 | 185.7 | 0 | 1091.4 | 769.3 | 7 | 0.63 | 14.84 |
| 105 | 397 | 0 | 185.7 | 0 | 1040.6 | 734.3 | 7 | 0.47 | 25.45 |
| 106 | 381.4 | 0 | 185.7 | 0 | 1104.6 | 784.3 | 28 | 0.49 | 22.49 |
| 107 | 295.8 | 0 | 185.7 | 0 | 1091.4 | 769.3 | 28 | 0.63 | 25.22 |
| 108 | 339.2 | 0 | 185.7 | 0 | 1069.2 | 754.3 | 7 | 0.55 | 21.18 |
| 109 | 381.4 | 0 | 185.7 | 0 | 1104.6 | 784.3 | 7 | 0.49 | 14.54 |
| 110 | 339.2 | 0 | 185.7 | 0 | 1069.2 | 754.3 | 28 | 0.55 | 31.9 |
| 111 | 382.5 | 0 | 185.7 | 0 | 1047.8 | 739.3 | 28 | 0.49 | 37.44 |
| 112 | 339 | 0 | 197 | 0 | 968 | 781 | 3 | 0.58 | 13.22 |
| 113 | 339 | 0 | 197 | 0 | 968 | 781 | 7 | 0.58 | 20.97 |
| 114 | 339 | 0 | 197 | 0 | 968 | 781 | 14 | 0.58 | 27.04 |
| 115 | 339 | 0 | 197 | 0 | 968 | 781 | 28 | 0.58 | 32.04 |
| 116 | 339 | 0 | 197 | 0 | 968 | 781 | 90 | 0.58 | 35.17 |
| 117 | 339 | 0 | 197 | 0 | 968 | 781 | 180 | 0.58 | 36.45 |
| 118 | 339 | 0 | 197 | 0 | 968 | 781 | 365 | 0.58 | 38.89 |
| 119 | 277 | 0 | 191 | 0 | 968 | 856 | 14 | 0.69 | 21.26 |
| 120 | 277 | 0 | 191 | 0 | 968 | 856 | 28 | 0.69 | 25.97 |
| 121 | 277 | 0 | 191 | 0 | 968 | 856 | 3 | 0.69 | 11.36 |
| 122 | 277 | 0 | 191 | 0 | 968 | 856 | 90 | 0.69 | 31.25 |
| 123 | 277 | 0 | 191 | 0 | 968 | 856 | 180 | 0.69 | 32.33 |
| 124 | 277 | 0 | 191 | 0 | 968 | 856 | 360 | 0.69 | 33.7 |
| 125 | 307 | 0 | 193 | 0 | 968 | 812 | 180 | 0.63 | 34.49 |
| 126 | 307 | 0 | 193 | 0 | 968 | 812 | 365 | 0.63 | 36.15 |
| 127 | 307 | 0 | 193 | 0 | 968 | 812 | 3 | 0.63 | 12.54 |
| 128 | 307 | 0 | 193 | 0 | 968 | 812 | 28 | 0.63 | 27.53 |
| 129 | 307 | 0 | 193 | 0 | 968 | 812 | 90 | 0.63 | 32.92 |
| 130 | 325 | 0 | 184 | 0 | 1063 | 783 | 7 | 0.57 | 17.54 |
| 131 | 325 | 0 | 184 | 0 | 1063 | 783 | 28 | 0.57 | 30.57 |
| 132 | 275 | 0 | 183 | 0 | 1088 | 808 | 7 | 0.67 | 14.2 |
| 133 | 275 | 0 | 183 | 0 | 1088 | 808 | 28 | 0.67 | 24.5 |
| 134 | 300 | 0 | 184 | 0 | 1075 | 795 | 7 | 0.61 | 15.58 |
| 135 | 300 | 0 | 184 | 0 | 1075 | 795 | 28 | 0.61 | 26.85 |
| 136 | 375 | 0 | 186 | 0 | 1038 | 758 | 7 | 0.5 | 26.06 |
| 137 | 375 | 0 | 186 | 0 | 1038 | 758 | 28 | 0.5 | 38.21 |
| 138 | 400 | 0 | 187 | 0 | 1025 | 745 | 28 | 0.47 | 43.7 |
| 139 | 400 | 0 | 187 | 0 | 1025 | 745 | 7 | 0.47 | 30.14 |
| 140 | 350 | 0 | 186 | 0 | 1050 | 770 | 7 | 0.53 | 20.28 |
| 141 | 350 | 0 | 186 | 0 | 1050 | 770 | 28 | 0.53 | 34.29 |
| 142 | 310 | 0 | 192 | 0 | 1012 | 830 | 3 | 0.62 | 11.85 |
| 143 | 310 | 0 | 192 | 0 | 1012 | 830 | 7 | 0.62 | 17.24 |
| 144 | 310 | 0 | 192 | 0 | 1012 | 830 | 28 | 0.62 | 27.83 |
| 145 | 310 | 0 | 192 | 0 | 1012 | 830 | 90 | 0.62 | 35.76 |
| 146 | 310 | 0 | 192 | 0 | 1012 | 830 | 120 | 0.62 | 38.7 |
| 147 | 331 | 0 | 192 | 0 | 1025 | 821 | 3 | 0.58 | 14.31 |
| 148 | 331 | 0 | 192 | 0 | 1025 | 821 | 7 | 0.58 | 17.44 |
| 149 | 331 | 0 | 192 | 0 | 1025 | 821 | 28 | 0.58 | 31.74 |
| 150 | 331 | 0 | 192 | 0 | 1025 | 821 | 90 | 0.58 | 37.91 |
| 151 | 331 | 0 | 192 | 0 | 1025 | 821 | 120 | 0.58 | 39.38 |
| 152 | 349 | 0 | 192 | 0 | 1056 | 809 | 3 | 0.55 | 15.87 |
| 153 | 349 | 0 | 192 | 0 | 1056 | 809 | 7 | 0.55 | 9.01 |
| 154 | 349 | 0 | 192 | 0 | 1056 | 809 | 28 | 0.55 | 33.61 |
| 155 | 349 | 0 | 192 | 0 | 1056 | 809 | 90 | 0.55 | 40.66 |
| 156 | 349 | 0 | 192 | 0 | 1056 | 809 | 120 | 0.55 | 40.86 |
| 157 | 296 | 0 | 186 | 0 | 1090 | 769 | 7 | 0.63 | 18.91 |
| 158 | 296 | 0 | 186 | 0 | 1090 | 769 | 28 | 0.63 | 25.18 |
| 159 | 297 | 0 | 186 | 0 | 1040 | 734 | 7 | 0.63 | 30.96 |
| 160 | 480 | 0 | 192 | 0 | 936 | 721 | 28 | 0.4 | 43.89 |
| 161 | 480 | 0 | 192 | 0 | 936 | 721 | 90 | 0.4 | 54.28 |
| 162 | 397 | 0 | 186 | 0 | 1040 | 734 | 28 | 0.47 | 36.94 |
| 163 | 281 | 0 | 186 | 0 | 1104 | 774 | 7 | 0.66 | 14.5 |
| 164 | 281 | 0 | 185 | 0 | 1104 | 774 | 28 | 0.66 | 22.44 |
| 165 | 500 | 0 | 200 | 0 | 1125 | 613 | 1 | 0.4 | 12.64 |
| 166 | 500 | 0 | 200 | 0 | 1125 | 613 | 3 | 0.4 | 26.06 |
| 167 | 500 | 0 | 200 | 0 | 1125 | 613 | 7 | 0.4 | 33.21 |
| 168 | 500 | 0 | 200 | 0 | 1125 | 613 | 14 | 0.4 | 36.94 |
| 169 | 500 | 0 | 200 | 0 | 1125 | 613 | 28 | 0.4 | 44.09 |
| 170 | 540 | 0 | 173 | 0 | 1125 | 613 | 7 | 0.32 | 52.61 |
| 171 | 540 | 0 | 173 | 0 | 1125 | 613 | 14 | 0.32 | 59.76 |
| 172 | 540 | 0 | 173 | 0 | 1125 | 613 | 28 | 0.32 | 67.31 |
| 173 | 540 | 0 | 173 | 0 | 1125 | 613 | 90 | 0.32 | 69.66 |
| 174 | 540 | 0 | 173 | 0 | 1125 | 613 | 180 | 0.32 | 71.62 |
| 175 | 540 | 0 | 173 | 0 | 1125 | 613 | 270 | 0.32 | 74.17 |
| 176 | 350 | 0 | 203 | 0 | 974 | 775 | 7 | 0.58 | 18.13 |
| 177 | 350 | 0 | 203 | 0 | 974 | 775 | 14 | 0.58 | 22.53 |
| 178 | 350 | 0 | 203 | 0 | 974 | 775 | 28 | 0.58 | 27.34 |
| 179 | 350 | 0 | 203 | 0 | 974 | 775 | 56 | 0.58 | 29.98 |
| 180 | 350 | 0 | 203 | 0 | 974 | 775 | 90 | 0.58 | 31.35 |
| 181 | 350 | 0 | 203 | 0 | 974 | 775 | 180 | 0.58 | 32.72 |
| 182 | 385 | 0 | 186 | 0 | 966 | 763 | 1 | 0.48 | 6.27 |
| 183 | 385 | 0 | 186 | 0 | 966 | 763 | 3 | 0.48 | 14.7 |
| 184 | 385 | 0 | 186 | 0 | 966 | 763 | 7 | 0.48 | 23.22 |
| 185 | 385 | 0 | 186 | 0 | 966 | 763 | 14 | 0.48 | 27.92 |
| 186 | 385 | 0 | 186 | 0 | 966 | 763 | 28 | 0.48 | 31.35 |
| 187 | 331 | 0 | 192 | 0 | 978 | 825 | 180 | 0.58 | 39 |
| 188 | 331 | 0 | 192 | 0 | 978 | 825 | 360 | 0.58 | 41.24 |
| 189 | 349 | 0 | 192 | 0 | 1047 | 806 | 3 | 0.55 | 14.99 |
| 190 | 331 | 0 | 192 | 0 | 978 | 825 | 3 | 0.58 | 13.52 |
| 191 | 382 | 0 | 186 | 0 | 1047 | 739 | 7 | 0.49 | 24 |
| 192 | 382 | 0 | 186 | 0 | 1047 | 739 | 28 | 0.49 | 37.42 |
| 193 | 382 | 0 | 186 | 0 | 1111 | 784 | 7 | 0.49 | 11.47 |
| 194 | 281 | 0 | 186 | 0 | 1104 | 774 | 28 | 0.66 | 22.44 |
| 195 | 339 | 0 | 185 | 0 | 1069 | 754 | 7 | 0.55 | 21.16 |
| 196 | 339 | 0 | 185 | 0 | 1069 | 754 | 28 | 0.55 | 31.84 |
| 197 | 295 | 0 | 185 | 0 | 1069 | 769 | 7 | 0.63 | 14.8 |
| 198 | 295 | 0 | 185 | 0 | 1069 | 769 | 28 | 0.63 | 25.18 |
| 199 | 296 | 0 | 192 | 0 | 1085 | 765 | 7 | 0.65 | 14.2 |
| 200 | 296 | 0 | 192 | 0 | 1085 | 765 | 28 | 0.65 | 21.65 |
| 201 | 296 | 0 | 192 | 0 | 1085 | 765 | 90 | 0.65 | 29.39 |
| 202 | 331 | 0 | 192 | 0 | 879 | 825 | 3 | 0.58 | 13.52 |
| 203 | 331 | 0 | 192 | 0 | 978 | 825 | 7 | 0.58 | 16.26 |
| 204 | 331 | 0 | 192 | 0 | 978 | 825 | 28 | 0.58 | 31.45 |
| 205 | 331 | 0 | 192 | 0 | 978 | 825 | 90 | 0.58 | 37.23 |
| 206 | 349 | 0 | 192 | 0 | 1047 | 806 | 7 | 0.55 | 18.13 |
| 207 | 349 | 0 | 192 | 0 | 1047 | 806 | 28 | 0.55 | 32.72 |
| 208 | 349 | 0 | 192 | 0 | 1047 | 806 | 90 | 0.55 | 39.49 |
| 209 | 349 | 0 | 192 | 0 | 1047 | 806 | 180 | 0.55 | 41.05 |
| 210 | 349 | 0 | 192 | 0 | 1047 | 806 | 360 | 0.55 | 42.13 |
| 211 | 302 | 0 | 203 | 0 | 974 | 817 | 14 | 0.67 | 18.13 |
| 212 | 302 | 0 | 203 | 0 | 974 | 817 | 180 | 0.67 | 26.74 |
| 213 | 525 | 0 | 189 | 0 | 1125 | 613 | 180 | 0.36 | 61.92 |
| 214 | 500 | 0 | 200 | 0 | 1125 | 613 | 90 | 0.4 | 47.22 |
| 215 | 500 | 0 | 200 | 0 | 1125 | 613 | 180 | 0.4 | 51.04 |
| 216 | 500 | 0 | 200 | 0 | 1125 | 613 | 270 | 0.4 | 55.16 |
| 217 | 540 | 0 | 173 | 0 | 1125 | 613 | 3 | 0.32 | 41.64 |
| 218 | 339 | 0 | 185 | 0 | 1060 | 754 | 28 | 0.55 | 31.65 |
| 219 | 393 | 0 | 192 | 0 | 940 | 758 | 3 | 0.49 | 19.11 |
| 220 | 393 | 0 | 192 | 0 | 940 | 758 | 28 | 0.49 | 39.58 |
| 221 | 393 | 0 | 192 | 0 | 940 | 758 | 90 | 0.49 | 48.79 |
| 222 | 382 | 0 | 185 | 0 | 1047 | 739 | 7 | 0.48 | 24 |
| 223 | 382 | 0 | 185 | 0 | 1047 | 739 | 28 | 0.48 | 37.42 |
| 224 | 310 | 0 | 192 | 0 | 970 | 850 | 7 | 0.62 | 14.99 |
| 225 | 310 | 0 | 192 | 0 | 970 | 850 | 28 | 0.62 | 27.92 |
| 226 | 310 | 0 | 192 | 0 | 970 | 850 | 90 | 0.62 | 34.68 |
| 227 | 310 | 0 | 192 | 0 | 970 | 850 | 180 | 0.62 | 37.33 |
| 228 | 310 | 0 | 192 | 0 | 970 | 850 | 360 | 0.62 | 38.11 |
| 229 | 525 | 0 | 189 | 0 | 1125 | 613 | 3 | 0.36 | 33.8 |
| 230 | 525 | 0 | 189 | 0 | 1125 | 613 | 7 | 0.36 | 42.42 |
| 231 | 525 | 0 | 189 | 0 | 1125 | 613 | 14 | 0.36 | 48.4 |
| 232 | 525 | 0 | 189 | 0 | 1125 | 613 | 28 | 0.36 | 55.94 |
| 233 | 525 | 0 | 189 | 0 | 1125 | 613 | 90 | 0.36 | 58.78 |
| 234 | 525 | 0 | 189 | 0 | 1125 | 613 | 270 | 0.36 | 67.11 |
| 235 | 322 | 0 | 203 | 0 | 974 | 800 | 14 | 0.63 | 20.77 |
| 236 | 322 | 0 | 203 | 0 | 974 | 800 | 28 | 0.63 | 25.18 |
| 237 | 322 | 0 | 203 | 0 | 974 | 800 | 180 | 0.63 | 29.59 |
| 238 | 302 | 0 | 203 | 0 | 974 | 817 | 28 | 0.67 | 21.75 |
| 239 | 397 | 0 | 185 | 0 | 1040 | 734 | 28 | 0.47 | 39.09 |
| 240 | 480 | 0 | 192 | 0 | 936 | 721 | 3 | 0.4 | 24.39 |
| 241 | 522 | 0 | 146 | 0 | 896 | 896 | 7 | 0.28 | 50.51 |
| 242 | 522 | 0 | 146 | 0 | 896 | 896 | 28 | 0.28 | 74.99 |
| 243 | 374 | 0 | 190 | 7 | 1013 | 730 | 28 | 0.51 | 39.05 |
| 244 | 305 | 100 | 196 | 10 | 959 | 705 | 28 | 0.64 | 30.12 |
| 245 | 298 | 107 | 186 | 6 | 879 | 815 | 28 | 0.62 | 42.64 |
| 246 | 318 | 126 | 210 | 6 | 861 | 737 | 28 | 0.66 | 40.06 |
| 247 | 356 | 142 | 193 | 11 | 801 | 778 | 28 | 0.54 | 40.87 |
| 248 | 314 | 113 | 170 | 10 | 925 | 783 | 28 | 0.54 | 38.46 |
| 249 | 321 | 128 | 182 | 11 | 870 | 780 | 28 | 0.57 | 37.26 |
| 250 | 298 | 107 | 210 | 11 | 880 | 744 | 28 | 0.7 | 31.87 |
| 251 | 322 | 116 | 196 | 10 | 818 | 813 | 28 | 0.61 | 31.18 |
| 252 | 313 | 113 | 178 | 8 | 1002 | 689 | 28 | 0.57 | 36.8 |
| 253 | 326 | 138 | 199 | 11 | 801 | 792 | 28 | 0.61 | 40.68 |
| 254 | 336 | 0 | 182 | 3 | 986 | 817 | 28 | 0.54 | 44.86 |
| 255 | 298 | 107 | 164 | 13 | 953 | 784 | 28 | 0.55 | 35.86 |
| 256 | 313 | 0 | 178 | 8 | 1000 | 822 | 28 | 0.57 | 25.1 |
| 257 | 313.3 | 113 | 178.5 | 8 | 1001.9 | 688.7 | 28 | 0.57 | 36.8 |
| 258 | 326.5 | 137.9 | 199 | 10.8 | 801.1 | 792.5 | 28 | 0.61 | 38.63 |
| 259 | 336.5 | 0 | 181.9 | 3.4 | 985.8 | 816.8 | 28 | 0.54 | 44.87 |
| 260 | 298.1 | 107.5 | 163.6 | 12.8 | 953.2 | 784 | 28 | 0.55 | 35.87 |
| 261 | 312.7 | 0 | 178.1 | 8 | 999.7 | 822.2 | 28 | 0.57 | 25.1 |
| 262 | 374.3 | 0 | 190.2 | 6.7 | 1013.2 | 730.4 | 28 | 0.51 | 39.06 |
| 263 | 304.8 | 99.6 | 196 | 9.8 | 959.4 | 705.2 | 28 | 0.64 | 30.12 |
| 264 | 298.1 | 107 | 186.4 | 6.1 | 879 | 815.2 | 28 | 0.63 | 42.64 |
| 265 | 317.9 | 126.5 | 209.7 | 5.7 | 860.5 | 736.6 | 28 | 0.66 | 40.06 |
| 266 | 355.9 | 141.6 | 193.3 | 11 | 801.4 | 778.4 | 28 | 0.54 | 40.87 |
| 267 | 313.8 | 112.6 | 169.9 | 10.1 | 925.3 | 782.9 | 28 | 0.54 | 38.46 |
| 268 | 321.4 | 127.9 | 182.5 | 11.5 | 870.1 | 779.7 | 28 | 0.57 | 37.27 |
| 269 | 298.2 | 107 | 209.7 | 11.1 | 879.6 | 744.2 | 28 | 0.7 | 31.88 |
| 270 | 322.2 | 115.6 | 196 | 10.4 | 817.9 | 813.4 | 28 | 0.61 | 31.18 |
Author Contributions
A.A. (Ayaz Ahmad)—conceptualization, modeling, and write up. F.F.—visualization and review. P.N.—writing, validation and supervision. K.O.—funding and review. A.A. (Arslan Akbar)—review, editing and visualization. F.A. and R.A.—data acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by Wroclaw University of Science and Technology.
Data Availability Statement
The data presented in this article is available within the article.
Conflicts of Interest
The authors declared no conflict of interest.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Zhang N., Duan H., Miller T.R., Tam V.W.Y., Liu G., Zuo J. Mitigation of carbon dioxide by accelerated sequestration in concrete debris. Renew. Sustain. Energy Rev. 2020;117:109495. doi: 10.1016/j.rser.2019.109495. [DOI] [Google Scholar]
- 2.Monkman S., MacDonald M. On carbon dioxide utilization as a means to improve the sustainability of ready-mixed concrete. J. Clean. Prod. 2017;167:365–375. doi: 10.1016/j.jclepro.2017.08.194. [DOI] [Google Scholar]
- 3.Qian X., Wang J., Fang Y., Wang L. Carbon dioxide as an admixture for better performance of OPC-based concrete. J. CO2 Util. 2018;25:31–38. doi: 10.1016/j.jcou.2018.03.007. [DOI] [Google Scholar]
- 4.Akbar A., Liew K.M. Assessing recycling potential of carbon fiber reinforced plastic waste in production of eco-efficient cement-based materials. J. Clean. Prod. 2020;274:123001. doi: 10.1016/j.jclepro.2020.123001. [DOI] [Google Scholar]
- 5.Jahanzaib Khalil M., Aslam M., Ahmad S. Utilization of sugarcane bagasse ash as cement replacement for the production of sustainable concrete—A review. Constr. Build. Mater. 2020:121371. doi: 10.1016/j.conbuildmat.2020.121371. [DOI] [Google Scholar]
- 6.Wang L., Chen L., Tsang D.C.W., Guo B., Yang J., Shen Z., Hou D., Ok Y.S., Poon C.S. Biochar as green additives in cement-based composites with carbon dioxide curing. J. Clean. Prod. 2020;258:120678. doi: 10.1016/j.jclepro.2020.120678. [DOI] [Google Scholar]
- 7.Kang S., Lloyd Z., Kim T., Ley M.T. Predicting the compressive strength of fly ash concrete with the Particle Model. Cem. Concr. Res. 2020;137:106218. doi: 10.1016/j.cemconres.2020.106218. [DOI] [Google Scholar]
- 8.Farooq F., Akbar A., Khushnood R.A., Muhammad W.L.B., Rehman S.K.U., Javed M.F. Experimental investigation of hybrid carbon nanotubes and graphite nanoplatelets on rheology, shrinkage, mechanical, and microstructure of SCCM. Materials. 2020;13:230. doi: 10.3390/ma13010230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Akbar A., Farooq F., Shafique M., Aslam F., Alyousef R., Alabduljabbar H. Sugarcane bagasse ash-based engineered geopolymer mortar incorporating propylene fibers. J. Build. Eng. 2021;33:101492. doi: 10.1016/j.jobe.2020.101492. [DOI] [Google Scholar]
- 10.Ghouleh Z., Shao Y. Turning municipal solid waste incineration into a cleaner cement production. J. Clean. Prod. 2018;195:268–279. doi: 10.1016/j.jclepro.2018.05.209. [DOI] [Google Scholar]
- 11.Lee M.G., Kang D., Jo H., Park J. Carbon dioxide utilization with carbonation using industrial waste-desulfurization gypsum and waste concrete. J. Mater. Cycles Waste Manag. 2016;18:407–412. doi: 10.1007/s10163-015-0461-0. [DOI] [Google Scholar]
- 12.Possan E., Thomaz W.A., Aleandri G.A., Felix E.F., dos Santos A.C.P. CO2 uptake potential due to concrete carbonation: A case study. Case Stud. Constr. Mater. 2017;6:147–161. doi: 10.1016/j.cscm.2017.01.007. [DOI] [Google Scholar]
- 13.Farooq F., Ahmed W., Akbar A., Aslam F., Alyousef R. Predictive modelling for sustainable high-performance concrete from industrial wastes: A comparison and optimization of models using ensemble learners. J. Clean. Prod. 2021;292:126032. doi: 10.1016/j.jclepro.2021.126032. [DOI] [Google Scholar]
- 14.Bin Khairul anuar M.A.R., Ngamkhanong C., Wu Y., Kaewunruen S. Recycled Aggregates Concrete Compressive Strength Prediction Using Artificial Neural Networks (ANNs) Infrastructures. 2021;6:17. doi: 10.3390/infrastructures6020017. [DOI] [Google Scholar]
- 15.Farooq F., Amin M.N., Khan K., Sadiq M.R., Javed M.F., Aslam F., Alyousef R. A comparative study of random forest and genetic engineering programming for the prediction of compressive strength of high strength concrete (HSC) Appl. Sci. 2020;10:7330. doi: 10.3390/app10207330. [DOI] [Google Scholar]
- 16.Javed M.F., Farooq F., Memon S.A., Akbar A., Khan M.A., Aslam F., Alyousef R., Alabduljabbar H., Rehman S.K.U., Ur Rehman S.K., et al. New Prediction Model for the Ultimate Axial Capacity of Concrete-Filled Steel Tubes: An Evolutionary Approach. Crystals. 2020;10:741. doi: 10.3390/cryst10090741. [DOI] [Google Scholar]
- 17.Iqbal M.F., Liu Q.F., Azim I., Zhu X., Yang J., Javed M.F., Rauf M. Prediction of mechanical properties of green concrete incorporating waste foundry sand based on gene expression programming. J. Hazard. Mater. 2020;384:121322. doi: 10.1016/j.jhazmat.2019.121322. [DOI] [PubMed] [Google Scholar]
- 18.De Domenico D., Ricciardi G. Shear strength of RC beams with stirrups using an improved Eurocode 2 truss model with two variable-inclination compression struts. Eng. Struct. 2019;198 doi: 10.1016/j.engstruct.2019.109359. [DOI] [Google Scholar]
- 19.Sadowski Ł., Nikoo M., Nikoo M. Concrete compressive strength prediction using the imperialist competitive algorithm. Comput. Concr. 2018;22:355–363. doi: 10.12989/cac.2018.22.4.355. [DOI] [Google Scholar]
- 20.Czarnecki S., Shariq M., Nikoo M., Sadowski Ł. An intelligent model for the prediction of the compressive strength of cementitious composites with ground granulated blast furnace slag based on ultrasonic pulse velocity measurements. Measurement. 2021:108951. doi: 10.1016/j.measurement.2020.108951. [DOI] [Google Scholar]
- 21.Sadowski Ł., Piechówka-Mielnik M., Widziszowski T., Gardynik A., Mackiewicz S. Hybrid ultrasonic-neural prediction of the compressive strength of environmentally friendly concrete screeds with high volume of waste quartz mineral dust. J. Clean. Prod. 2019;212:727–740. doi: 10.1016/j.jclepro.2018.12.059. [DOI] [Google Scholar]
- 22.Javed M.F., Amin M.N., Shah M.I., Khan K., Iftikhar B., Farooq F., Aslam F., Alyousef R., Alabduljabbar H. Applications of gene expression programming and regression techniques for estimating compressive strength of bagasse ash based concrete. Crystals. 2020;10:737. doi: 10.3390/cryst10090737. [DOI] [Google Scholar]
- 23.Aslam F., Farooq F., Amin M.N., Khan K., Waheed A., Akbar A., Javed M.F., Alyousef R., Alabdulijabbar H. Applications of Gene Expression Programming for Estimating Compressive Strength of High-Strength Concrete. Adv. Civ. Eng. 2020 doi: 10.1155/2020/8850535. [DOI] [Google Scholar]
- 24.Naderpour H., Rafiean A.H., Fakharian P. Compressive strength prediction of environmentally friendly concrete using artificial neural networks. J. Build. Eng. 2018;16:213–219. doi: 10.1016/j.jobe.2018.01.007. [DOI] [Google Scholar]
- 25.Getahun M.A., Shitote S.M., Abiero Gariy Z.C. Artificial neural network based modelling approach for strength prediction of concrete incorporating agricultural and construction wastes. Constr. Build. Mater. 2018;190:517–525. doi: 10.1016/j.conbuildmat.2018.09.097. [DOI] [Google Scholar]
- 26.Liu Q., Iqbal M.F., Yang J., Lu X., Zhang P., Rauf M. Prediction of chloride diffusivity in concrete using artificial neural network: Modelling and performance evaluation. Constr. Build. Mater. 2020;268:121082. doi: 10.1016/j.conbuildmat.2020.121082. [DOI] [Google Scholar]
- 27.Ahmad T., Chen H., Huang R., Yabin G., Wang J., Shair J., Azeem Akram H.M., Hassnain Mohsan S.A., Kazim M. Supervised based machine learning models for short, medium and long-term energy prediction in distinct building environment. Energy. 2018;158:17–32. doi: 10.1016/j.energy.2018.05.169. [DOI] [Google Scholar]
- 28.Wang P., Zheng X., Li J., Zhu B. Prediction of epidemic trends in COVID-19 with logistic model and machine learning technics. Chaos Solitons Fractals. 2020;139:110058. doi: 10.1016/j.chaos.2020.110058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cladera A., Marí A.R. Shear design procedure for reinforced normal and high-strength concrete beams using artificial neural networks. Part I: Beams without stirrups. Eng. Struct. 2004;26:917–926. doi: 10.1016/j.engstruct.2004.02.010. [DOI] [Google Scholar]
- 30.Onyari E.K., Ikotun B.D. Prediction of compressive and flexural strengths of a modified zeolite additive mortar using artificial neural network. Constr. Build. Mater. 2018;187:1232–1241. doi: 10.1016/j.conbuildmat.2018.08.079. [DOI] [Google Scholar]
- 31.Feng D.C., Liu Z.T., Wang X.D., Chen Y., Chang J.Q., Wei D.F., Jiang Z.M. Machine learning-based compressive strength prediction for concrete: An adaptive boosting approach. Constr. Build. Mater. 2020;230:117000. doi: 10.1016/j.conbuildmat.2019.117000. [DOI] [Google Scholar]
- 32.Feng D.C., Liu Z.T., Wang X.D., Jiang Z.M., Liang S.X. Failure mode classification and bearing capacity prediction for reinforced concrete columns based on ensemble machine learning algorithm. Adv. Eng. Inform. 2020;45 doi: 10.1016/j.aei.2020.101126. [DOI] [Google Scholar]
- 33.Bui D.K., Nguyen T., Chou J.S., Nguyen-Xuan H., Ngo T.D. A modified firefly algorithm-artificial neural network expert system for predicting compressive and tensile strength of high-performance concrete. Constr. Build. Mater. 2018;180:320–333. doi: 10.1016/j.conbuildmat.2018.05.201. [DOI] [Google Scholar]
- 34.Salami B.A., Rahman S.M., Oyehan T.A., Maslehuddin M., Al Dulaijan S.U. Ensemble machine learning model for corrosion initiation time estimation of embedded steel reinforced self-compacting concrete. Meas. J. Int. Meas. Confed. 2020;165:108141. doi: 10.1016/j.measurement.2020.108141. [DOI] [Google Scholar]
- 35.Cai R., Han T., Liao W., Huang J., Li D., Kumar A., Ma H. Prediction of surface chloride concentration of marine concrete using ensemble machine learning. Cem. Concr. Res. 2020;136:106164. doi: 10.1016/j.cemconres.2020.106164. [DOI] [Google Scholar]
- 36.Aydogmus H.Y., Erdal H.I., Karakurt O., Namli E., Turkan Y.S., Erdal H. A comparative assessment of bagging ensemble models for modeling concrete slump flow. Comput. Concr. 2015;16:741–757. doi: 10.12989/cac.2015.16.5.741. [DOI] [Google Scholar]
- 37.Erdal H.I. Two-level and hybrid ensembles of decision trees for high performance concrete compressive strength prediction. Eng. Appl. Artif. Intell. 2013;26:1689–1697. doi: 10.1016/j.engappai.2013.03.014. [DOI] [Google Scholar]
- 38.Zounemat-Kermani M., Stephan D., Barjenbruch M., Hinkelmann R. Ensemble data mining modeling in corrosion of concrete sewer: A comparative study of network-based (MLPNN & RBFNN) and tree-based (RF, CHAID, & CART) models. Adv. Eng. Inform. 2020;43:101030. doi: 10.1016/j.aei.2019.101030. [DOI] [Google Scholar]
- 39.Lichman M. UCI Machine Learning Repository. University of California, School of Information and Computer Science; Irvine, CA, USA: 2013. [(accessed on 27 November 2020)]. Available online: http://archive.ics.uci.edu/ml. [Google Scholar]
- 40.Karbassi A., Mohebi B., Rezaee S., Lestuzzi P. Damage prediction for regular reinforced concrete buildings using the decision tree algorithm. Comput. Struct. 2014;130:46–56. doi: 10.1016/j.compstruc.2013.10.006. [DOI] [Google Scholar]
- 41.Ben Chaabene W., Flah M., Nehdi M.L. Machine learning prediction of mechanical properties of concrete: Critical review. Constr. Build. Mater. 2020;260:119889. doi: 10.1016/j.conbuildmat.2020.119889. [DOI] [Google Scholar]
- 42.Ribeiro M.H.D.M., dos Santos Coelho L. Ensemble approach based on bagging, boosting and stacking for short-term prediction in agribusiness time series. Appl. Soft Comput. J. 2020;86:105837. doi: 10.1016/j.asoc.2019.105837. [DOI] [Google Scholar]
- 43.Dou J., Yunus A.P., Bui D.T., Merghadi A., Sahana M., Zhu Z., Chen C.W., Han Z., Pham B.T. Improved landslide assessment using support vector machine with bagging, boosting, and stacking ensemble machine learning framework in a mountainous watershed, Japan. Landslides. 2020;17:641–658. doi: 10.1007/s10346-019-01286-5. [DOI] [Google Scholar]
- 44.Kaboli S.H.A., Fallahpour A., Selvaraj J., Rahim N.A. Long-term electrical energy consumption formulating and forecasting via optimized gene expression programming. Energy. 2017;126:144–164. doi: 10.1016/j.energy.2017.03.009. [DOI] [Google Scholar]
- 45.Ferreira C. Soft Computing and Industry. Springer; London, UK: 2002. Gene Expression Programming in Problem Solving; pp. 635–653. [Google Scholar]
- 46.Shah M.I., Javed M.F., Abunama T. Proposed formulation of surface water quality and modelling using gene expression, machine learning, and regression techniques. Environ. Sci. Pollut. Res. 2020:1–19. doi: 10.1007/s11356-020-11490-9. [DOI] [PubMed] [Google Scholar]
- 47.Khan M.A., Memon S.A., Farooq F., Javed M.F., Aslam F., Alyousef R. Compressive Strength of Fly-Ash-Based Geopolymer Concrete by Gene Expression Programming and Random Forest. Adv. Civ. Eng. 2021;2021:1–17. doi: 10.1155/2021/6618407. [DOI] [Google Scholar]
- 48.Kohavi R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection; Proceedings of the International Joint Conference of Artificial Intelligence; Montreal, QC, Canada. 20–25 August 1995. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data presented in this article is available within the article.