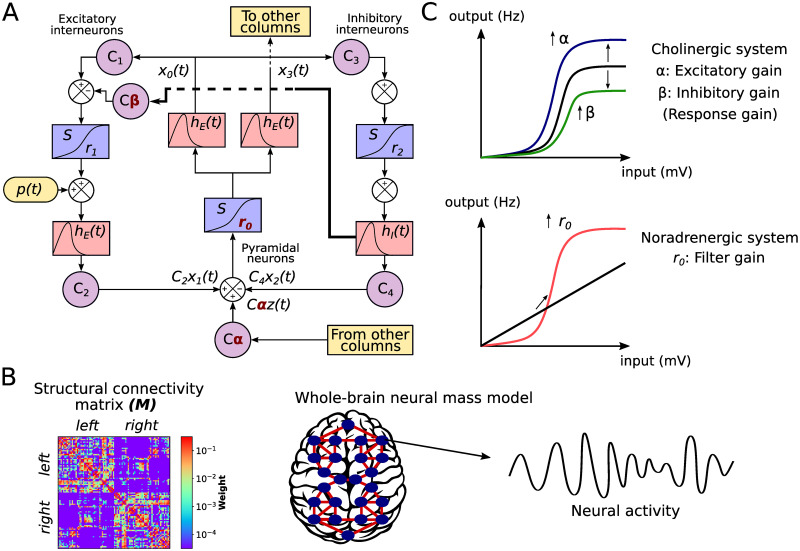
Fig 1. Whole-brain neural mass model.

A) The Jansen & Rit model is constituted by a population of pyramidal neurons with excitatory and inhibitory feedback mediated by interneurons (INs). Each population is connected by a series of constants C_i. The outputs are transformed from average pulse density to average postsynaptic membrane potential by an excitatory (inhibitory) impulse response function h_E(t) (h_I(t)). Then, a sigmoid function S performs the inverse operation. Pyramidal neurons project to distant cortical columns, and receive both uncorrelated Gaussian-distributed inputs p(t) and inputs from other cortical columns z(t). Neuromodulation is constituted by three parameters, colored in red: excitatory gain α, which scales z(t), inhibitory gain β, which increases the inhibitory input to excitatory INs (thick line), and filter gain, r₀, which modifies the slope of the sigmoid function in pyramidal neurons. B) Each node represents a cortical column, whose dynamics is ruled by the Jansen & Rit equations. Nodes are connected through a structural connectivity matrix, M C) Neuromodulation modifies the coupling between neurons and the properties of the input (average postsynaptic membrane potential) to output (average pulse density) sigmoid function. The cholinergic system modifies the global coupling and local inhibition. α amplifies the response of pyramidal neurons to other columns’ input; it also increases pyramidal neurons excitability. β amplifies the effect of inhibitory INs to excitatory INs, damping pyramidal cells excitability. The noradrenergic system increments the responsivity of pyramidal neurons to relevant stimuli respect to noise, as a filter, by increasing the slope r₀ of their sigmoid function.