Fig. 11.

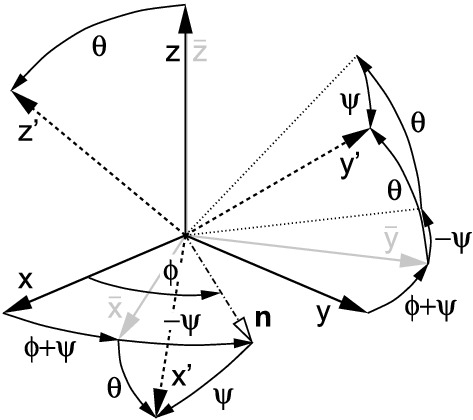
The calculation of the torsion angle $\xi =\varphi +\psi$ and the stick coordinate system ${\overline{\mathcal{K}}}_1$ ($\overline{\mathsf{x}}$-$\overline{\mathsf{y}}$-$\overline{\mathsf{z}}$) at the instant of a ‘stick’ event: separating the tilt from the torsion contribution to an overall rotation of the primed coordinate system ${\mathcal{K}}_1$ (dashed axes) relative to the unprimed system ${\mathcal{K}}_0$ (solid axes). The rotations are expressed in terms of Euler angles executed in the order $\varphi ,\theta ,\psi$. The tilt is the (second) angular rotation by $\theta$ around the $\mathsf{n}$-axis, the latter being the intermediate $\mathsf{x}$-axis after the first rotation around the initial (unprimed) $\mathsf{z}$-axis by $\varphi$. The last (third) rotation by $\psi$ is then executed around the already finally fixed (primed) ${\mathsf{z}}^{\prime }$-axis. The $\mathsf{x}$-$\mathsf{y}$-plane of the (solid, unprimed) ${\mathcal{K}}_0$ system is the contact plane, in which to lie the $\mathsf{n}$-axis of tilting can be assumed and used for parameterising stick–slip interaction when applying the Euler angle description of three-dimensional rotations. Regardless of the angular orientation of ${\mathcal{K}}_1$ relative to ${\mathcal{K}}_0$, the position of the origin of ${\mathcal{K}}_1$ in relation to the contact plane determines (a) whether both coordinate systems (bodies) are in contact at all and, therefore, mechanically interact by a force $\mathbf{f}$ and a torque $\mathit{\tau }$, as well as (b) where in the contact plane a unique stick coordinate system ${\overline{\mathcal{K}}}_1$ is located for modelling a restoring viscoelastic tangential force and torsional torque in the ‘stick’ state. In fact, ${\overline{\mathcal{K}}}_1$ is fixed at the instant when the ‘stick’ event occurs: its origin is chosen to be located in the contact plane at the vector ${\overline{\mathbf{r}}}_{\Vert }$ of the projection of ${\mathcal{K}}_1$’s origin onto the contact plane—here, for simplicity of the illustration at ${\mathcal{K}}_0$’s origin—, the orientation of ${\overline{\mathcal{K}}}_1$’s $\overline{\mathsf{z}}$-axis is chosen to always align with the normal vector of the contact plane (${\mathcal{K}}_0$’s $\mathsf{z}$-axis), and the Euler angle sum $\overline{\xi }=\overline{\varphi }+\overline{\psi }$ is calculated for determining later torsional angular excursions $\Delta \xi =\xi -\overline{\xi }$ relative to the ‘stick’ condition