Fig. 1.

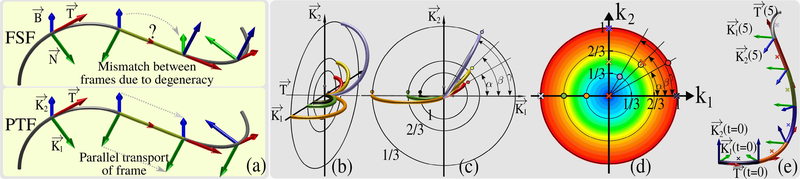
(a) For FSF, $\overrightarrow{T}$, $\overrightarrow{N}$ and $\overrightarrow{B}$ are local and unique. For PTF, $\overrightarrow{T}$ is local and unique but ${\overrightarrow{K}}_1$ and ${\overrightarrow{K}}_2$ can be any two perpendicular vectors that are orthogonal to $\overrightarrow{T}$. Due to the degeneracy of FSF along straight lines (shown in yellow), FSF needs to be rotated during propagation [6]. Because PTF does not suffer from this weakness, rotation of the frame is not required, which makes it a superior approach for tractography. (b-c) show different half circles obtained using the same F(0) but with different k₁ and k₂ which are marked with “∘” using matching colors in (d). Color gradient in (d) shows the increasing curvature from 0 (blue) to 1 (red). (e) shows the propagation of a curve between t = [0, 6] with segment lengths of Δt = 1 that are shown in different colors. The only inputs are F[0] and the k₁[nΔt], k₂[nΔt] pairs at n = (0, 1, 2, 3, 4, 5) that are shown with “×” using matching colors in (d). F[(n + 1)Δt] are calculated for each n > 0 using Eq.7.