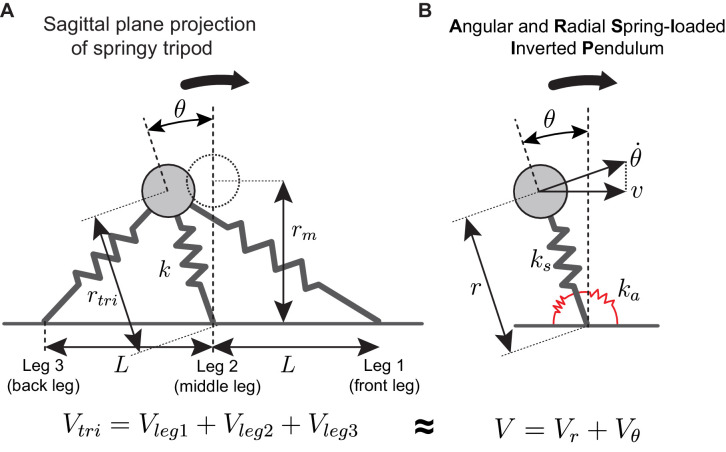
Figure 5. The angular and radial spring-loaded inverted pendulum (ARSLIP) model is equivalent to the springy tripod model.

(A) The sagittal plane mechanics is governed by the sagittal plane projection of the springy tripod. The arrow denotes the direction of motion. The parameters that define the springy tripod model are shown. The overall stiffness of the springy tripod is determined by the spring constant of individual legs, k, the height of the tripod (r_m), and the distance between the front and back legs (2L). See Table 1 as well. The behavior of the springy tripod is described by how the coordinates of the point mass – r and $\theta$ – change with time. (B) The sagittal plane projection of a springy tripod can be modeled as the ARSLIP model. The parameters that describe the ARSLP model are shown. Just like the springy tripod, ARSLIP is described by how the coordinates of the point mass – r and $\theta$ – change with time. The potential energy of the tripod can be derived as a sum of the elastic energies of the three legs. The ARSLIP potential energy can be derived by summing radial and angular potential energies. The equivalence of the two models is shown by finding parameter set for ARSLIP where the potential energies as a function of r and $\theta$ are similar when $\theta$ is small and changes in r are small (derived in 'Materials and methods').