Accurate detection of spontaneous seizures using a generalized linear model with external validation

Abstract

Objective:

Seizure detection is a major facet of electroencephalography (EEG) analysis in neurocritical care, epilepsy diagnosis and management, and the instantiation of novel therapies such as closed-loop stimulation or optogenetic control of seizures. It is also of increased importance in high-throughput, robust, and reproducible pre-clinical research. However, seizure detectors are not widely relied upon in either clinical or research settings due to limited validation. In this study, we create a high-performance seizure-detection approach, validated in multiple data sets, with the intention that such a system could be available to users for multiple purposes.

Methods:

We introduce a generalized linear model trained on 141 EEG signal features for classification of seizures in continuous EEG for two data sets. In the first (Focal Epilepsy) data set consisting of 16 rats with focal epilepsy, we collected 1012 spontaneous seizures over 3 months of 24/7 recording. We trained a generalized linear model on the 141 features representing 20 feature classes, including univariate and multivariate, linear and nonlinear, time, and frequency domains. We tested performance on multiple hold-out test data sets. We then used the trained model in a second (Multifocal Epilepsy) data set consisting of 96 rats with 2883 spontaneous multifocal seizures.

Results:

From the Focal Epilepsy data set, we built a pooled classifier with an Area Under the Receiver Operating Characteristic (AUROC) of 0.995 and leave-one-out classifiers with an AUROC of 0.962. We validated our method within the independently constructed Multifocal Epilepsy data set, resulting in a pooled AUROC of 0.963. We separately validated a model trained exclusively on the Focal Epilepsy data set and tested on the held-out Multifocal Epilepsy data set with an AUROC of 0.890. Latency to detection was under 5 seconds for over 80% of seizures and under 12 seconds for over 99% of seizures.

Significance:

This method achieves the highest performance published for seizure detection on multiple independent data sets. This method of seizure detection can be applied to automated EEG analysis pipelines as well as closed loop interventional approaches, and can be especially useful in the setting of research using animals in which there is an increased need for standardization and high-throughput analysis of large number of seizures.

1 |. INTRODUCTION

Epilepsy as a disease presents a unique challenge to patients, physicians, and researchers: Seizure, the key pathological brain state of interest, occurs only a small fraction of the time. For the ~30% of patients whose seizures remain refractory to antiepileptic medications, automatically identifying their seizures on EEG may be a crucial task in developing therapies.¹ This is particularly true as the field moves toward high-throughput multicenter pre-clinical animal trials with large numbers of animals and even larger numbers of seizures.

Considerable work has been done toward a reliable and fast seizure detector, but challenges remain, namely: (a) maintaining a low rate of false positives; (b) achieving low-latency detection; and perhaps most importantly, (c) generalizing to new patients or other data sets with different recording modalities.^2–5 To address these challenges, we introduce a general purpose seizure-detection model and assess its validity by applying it to two discrete large EEG data sets. Our objective is to formulate a uniform approach that performs well for a range of seizure-detection applications.

We aimed to record over 1000 labeled seizures to ensure that the test performance is a reflection of the general detection power of the algorithm and not of overfitting to a small data set.² In clinical data sets, each subject rarely has more than 10 seizures recorded, resulting in models failing to validate when applied to external data sets.^3,4 We created our own data set using the kainic acid unilateral focal epilepsy model in rats, which reliably models mesial temporal lobe epilepsy (mTLE).^6–8 In these rats, we could record 24/7 for months to collect 1012 seizures, with an average of 54.0 ± 81.6 seizures per animal, an order of magnitude higher than existing public human EEG data sets.² Invasive recordings in animals also allow for a more information-rich dataset: depth recordings better approximate responsive neurostimulation (RNS) paradigms, wherein an implanted device records neuronal activity and delivers stimulation.¹

Several seizure detection methods use a single feature type, such as a power spectrogram, as feature input.^9–11 In our approach, we utilize twenty distinct feature classes in the time and frequency domains. Basic single-channel features such as root mean square and coastline computed in the time domain are broadly descriptive of seizures and other hyperexcitation events.^12,13 Time domain features such as Hjorth parameters capture changes particular to EEG signals that may be pertinent to seizure detection.¹⁴ Additional frequency domain features including band powers and spectral edge frequency are effective due to their characteristic spectrographic signatures during a seizure.^9,10 Finally, multichannel features such as cross-correlation and phase synchronization index can specifically represent ictogenic synchronization.^15,16 (See Table 1 in Methods for a complete summary of all features used.)

TABLE 1.

Features computed on EEG signals as input into classifier model

Feature	Description	Domain
RMS	Root-mean square of signal13	Time
Coastline	Absolute sum of signal derivative36	Time
Skewness	Asymmetry of signal probability distribution45	Time
Kurtosis	Flatness of signal probability distribution45	Time
Autocorrelation function	Linear correlation of signal with itself on lag45	Time
Hjorth parameters	Activity, mobility, complexity of EEG signal14	Time
Maximal cross-correlation	Correlation of two channel signals, with one on lag45	Time
Nonlinear energy	Energy content of linear oscillator46	Time
Shannon entropy	Entropy of signal $\underset{i}{-\sum }{p}_i\log \left(p_i\right)$47	Time
Renyi entropy	Entropy $\frac{1}{1-\alpha }\log \sum _i{p}_i^{\alpha }$ for quadratic (α = 2)47	Time
Spikes	Event thresholded by amplitude, duration, derivative 36	Time
Fractal dimension	Similarity of signals at multiple scales48	Time
Phase synchronization index	Mean phase coherence between two channels15	Time
Band power	Power spectral density by frequency band45	Frequency
Normalized band power	Band power normalized by total power45	Frequency
Spectral edge frequency	Minimum frequency with 90% of power retained45	Frequency
Coherence	Linear synchronization of signals by band 45	Frequency
Spectral entropy	Signal complexity binned by frequency49	Frequency
State entropy	Entropy as a ratio of low and high bands49	Frequency
Response entropy	Entropy as a ratio of low and high bands49	Frequency
High-frequency oscillations	Event thresholded for signal filtered in [80, 200] Hz50	Frequency

Classification algorithms have ranged from thresholding on a principal component analysis (PCA) of the features to neural networks with complex architectures.^9,17–19 In previous studies, performance has not been reported uniformly, and many data sets are proprietary, precluding precise performance comparisons. Nevertheless, we have identified performance benchmarks in recent seizure-detection studies on EEG data, each reporting an Area Under the Receiver Operating Characteristic (AUROC) in the range of 0.990 to 0.995. One study used a convolutional neural network (CNN) trained on a two-dimensional (2D) image of raw EEG waveforms in a mouse model, yielding an AUROC of 0.993.²⁰ Another used a random forest classifier trained on envelopes of wavelet coefficients to produce the highest performing AUROC of 0.995.²¹ Table S1 has a summary of performance in other recent seizure-detection studies.

We aim to study whether one high-performing detector can be trained to perform well on independent EEG data sets representing different epilepsies. Using the highest performing features identified in past studies (see Table 1), we trained a generalized linear model (GLM) with a logit link function, a highly interpretable statistical method that performs well with regularization for feature-rich data; this approach allows an assumption of a Bernoulli distribution for the response variable, which is well-suited for a binary response (ictal versus nonictal).^22,23 We sought to test the validity of this model and approach on held-out test data of two separately constructed data sets modeling epilepsy in rats.

2 |. METHODS

2.1 |. Data acquisition

All procedures were performed in accordance with institutional and national guidelines for animal care and use for research purposes, and the study protocol was approved by the Massachusetts General Hospital Institutional Animal Care and Use Committee (IACUC). We implanted young (age 2–3 months, n = 15) wild-type male Sprague-Dawley rats with surface electrodes, electromyography (EMG) pads, and intrahippocampal depth electrodes bilaterally. We induced anesthesia for surgery via nebulized isoflurane (1%−3%) and drilled burr hole craniotomies for implantation of electrocorticography (ECoG) and local field potential (LFP) electrodes. We implanted the rats with standard electrodes for recording neural activity from the One Channel Electrode System (PlasticsOne, Inc). In each animal, we placed a screw electrode for ECoG overlying left parietal cortex (anteroposterior [AP] = −3 mm, mediolateral [ML] = −3 mm) and depth monopolar electrodes for LFP bilaterally into hippocampal CA3 (AP = −5.3 mm, ML = ±4.5 mm, dorsoventral [DV] = 6 mm). We also placed a guide cannula made from a 23G needle alongside the left hippocampal depth electrode. We inserted an EMG pad electrode underneath the trapezius muscular plane of the neck. Finally, we placed our reference electrode in the frontal bone and the ground electrode in the occipital bone.

Following complete recovery from the surgery (after a minimum of 3 days), microinjections of kainic acid (400 nL of 2.0 g/L in 0.9% saline) were administered into left hippocampal CA3 via the guide cannulas. The microinjection was done through a custom injector made of fused silica tubing fitted to the cannula. These kainic acid microinjections induced behavioral status epilepticus ~15 minutes after infusion, which was always self-limited within 3 hours, without the need for benzodiazepine rescue. Following recovery, rats developed spontaneous recurrent seizures an average of 23.1 ± 7.5 days post-SE (status epilepticus). We developed a rodent epilepsy monitoring unit (EMU) to monitor the physiology and behavior of our subjects. We recorded EEG and video from these subjects 24/7 for 3 months, with 99.8% uptime overall (animals had to be occasionally removed from the EMU for monitoring and care). We developed a custom set of hardware and software tools to acquire and analyze video and EEG data. We used the OpBox system (KimchiLab.org/opbox) for EEG recording, and a script using the OpenCV and skvideo Python libraries for video recording. We acquired EEG signals at 1 kS/s and video at 30 fps. The resultant data set from these experiments is henceforth referred to as the Focal Epilepsy data set.

We obtained an additional, larger and more varied rodent seizure data set from the contract site of the National Institute of Neurological Disorders and Stroke funded Epilepsy Therapy Screening Program (ETSP) at the University of Utah, which allowed us to test this approach in a dataset with a distinct seizure etiology.^24,25 This data set (Multifocal Epilepsy) includes EEG data from rats with multifocal epilepsy as induced by systemic injections of kainic acid. The procedures pertaining to animal use and care for this data set have been outlined previously.²⁴ These rats were recorded continuously with single channel EEG and video for weeks at a time. Because these animals were receiving antiepileptic drugs as part of ETSP, the EEG data used from these animals for this analysis included only the treatment-free periods, with baseline levels of seizure activity. Data were acquired using a custom setup using a Biopac MP150 at 500 Hz, band-pass filtered between 1 to 100 Hz, as described previously.²⁶

2.2 |. Data labeling

We identified events of interest including seizures, epileptiform discharges, and interictal spikes by thresholding line length of the left parietal ECoG at two standard deviations above mean. For the Focal Epilepsy data set, authors AK, SE, and SSC, trained in EEG pattern labeling, reviewed the output from this nonspecific event detector, and labeled specific events according to EEG morphology, including seizures. For these ground truth labels, we used the clinical definition of a seizure as an evolving, rhythmic, high-amplitude signal across multiple EEG channels, lasting at least 10 seconds.^27,28 We established a censorship criterion that if a subject had five or fewer seizures and met early end point criteria with less than 1 month of recording, we would exclude it from the analysis. For the Multifocal Epilepsy data set, the seizures were manually annotated by expert reviewers (authors KET and TGN) by the same process and definitions described earlier.

We validated selected seizures by observing the corresponding video on an as-needed basis for EEG traces that were potentially representative of a new seizure type for each animal. We observed multiple convulsive seizures for every subject on video. To fully capture the distribution of seizures needing detection, we included seizures rated Racine 0–5, with Racine 0 being those seizures that did not produce tonic-clonic activity of any kind. However, in order to ensure reproducibility, we did not include spike-wave discharges or other epileptiform events that are interrupted with mild sensory stimulus; these events are morphological correlates of nonseizure interictal discharges.²⁹

2.3 |. Feature extraction

Once the seizure segment was identified, we extracted the data and processed it by detrending and applying notch filters at 60, 120, and 180 Hz. In the nonictal data, we included the entire hour of data preceding every seizure, with a 30 second buffer. We also included 1 hour of data selected from 10 randomly chosen interictal segments (to maintain a reasonable computational load while sampling representative nonictal data), each of which was at least 2 hours away from a seizure. Thus, our sampled data were representative of all relevant nonictal states. For our pooled data set, we used 3054 ictal windows from 1012 seizures and 995 588 nonictal windows from the nonictal (interictal and preictal) segments. For both data sets, we computed the features shown in Table 1 on these segments, divided into 10-second windows, which is the minimum duration for a seizure. We computed 141 features using three channels (ECoG, left hippocampal LFP, and right hippocampal LFP) and seven frequency bands. These bands were as follows: 0.5–4 Hz (delta), 4–8 Hz (theta), 8–12 Hz (alpha), 12–16 Hz (spindle), 16–25 Hz (beta), 25–50 Hz (gamma), and 70–100 Hz (high gamma). Feature values for all windows were standardized within 1-hour periods.

2.4 |. Classification

In the Focal Epilepsy data set, we assess three different models of seizure detectors: (a) pooled, (b) continuous, and (c) extrapolated. (a) In the pooled model, we include data from all subjects equally weighted in the training data, and measure performance on the test data (held-out data), also drawn from all subjects; this approach aligns with best practices for algorithm performance comparison in the field.⁵ (b) We then trained a model while holding out for the test set the last 24 hours leading up to and including the final seizure for each subject. This approach approximates the clinical scenario of simultaneously recording seizure data from many patients and analyzing them in aggregate to detect future seizures for all patients and then applying the resulting detector to new data. (c) The extrapolated model is a leave-one-out test in which we train on data from all subjects except one, and test on this subject. This approximates the clinical application in which new patient data are analyzed with a detector trained on other patients (which can later be tuned by incorporating weighted data from the new patient).

Our machine learning approach is outlined in Figure 1E. We first randomly split each data set into 80% training data and 20% hold-out test data. When splitting the feature windows into the train and test sets, we grouped all data from within the same ictal or nonictal segments, thus avoiding any correlation between the sets that could cause overfitting. We then implemented fivefold cross-validation, using grid search to identify the optimal hyperparameters. The loss function employed for hyperparameter tuning was (1-AUROC) to equally weight sensitivity and specificity. We utilized PCA for dimensionality reduction and visualization of the feature space. Final performance was determined by the loss computed on the hold-out 20% of the data. We used this paradigm to train GLMs with a ridge penalty, with an assumption of a binomial distribution, due to the fixed number of independent binary classification events in our system. The hyperparameters in the grid search were the number of principal components used for classification and the ridge coefficient. We also sought to assess the ability of this approach to yield low-latency detection. To obtain a finer 1-second resolution of latency in the Focal Epilepsy data set, we recapitulated the same analysis on 5-second feature windows, this time using an 80% overlap. To validate our method, we applied the same methods for the pooled model to the Multifocal Epilepsy data set. To assess the external validity of the Focal Epilepsy model itself, we tested a GLM trained on the single ECoG channel of Focal Epilepsy data on the Multifocal Epilepsy data set.

FIGURE 1.

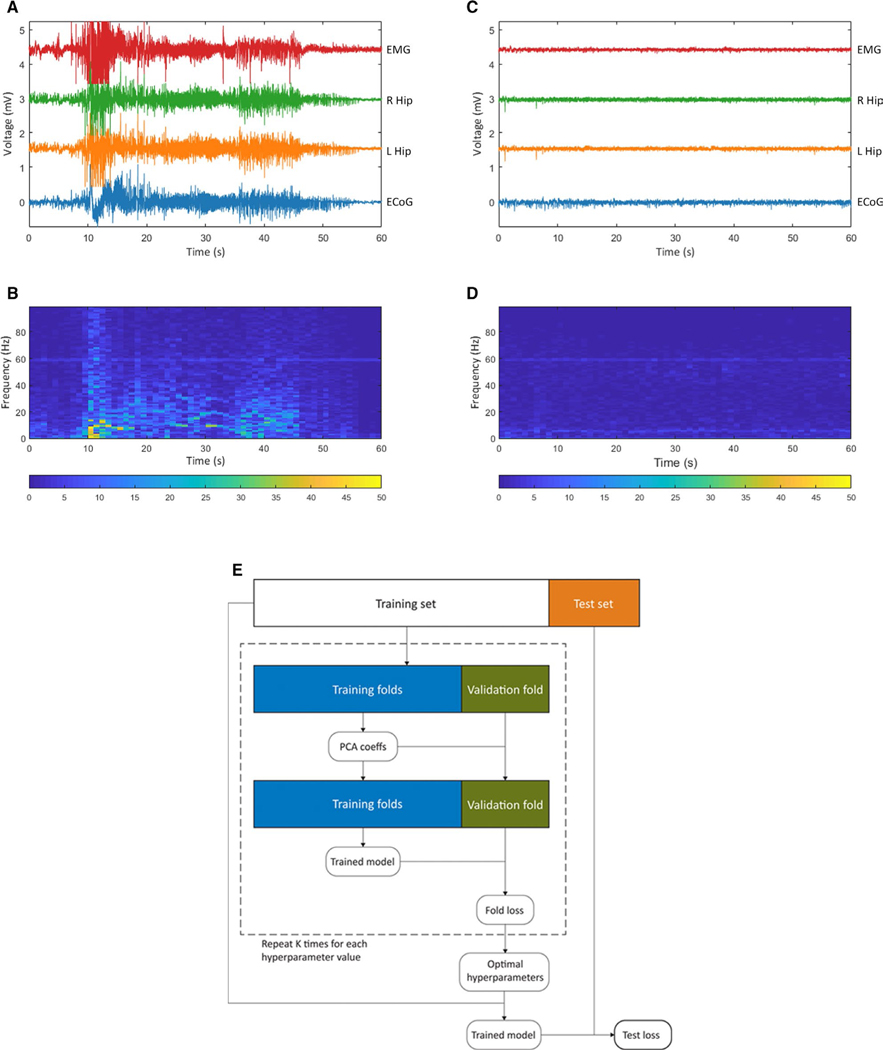
A seizure-detection paradigm for training ictal vs nonictal electroencephalography (EEG) classifier. A, An electrographic recording of a spontaneous seizure in a subject from the Focal Epilepsy data set, corresponding to Racine 5 behavior observed on video. EMG, electromyography channel; R Hip, right hippocampal depth local field potential (LFP) channel; L Hip, left hippocampal depth LFP channel; ECoG, left parietal electrocorticography channel. B, The ECoG spectrogram corresponding to this seizure. (C,D) Analogous to A and B but for an interictal (nonictal) period of EEG for the same subject. E, Flowchart of machine learning approach employed for training a generalized linear model

3. |. RESULTS

Labeling seizures with these predefined criteria led to the Focal Epilepsy data set consisting of 1012 labeled seizures from 16 rats, and the Multifocal Epilepsy data set comprising 2883 seizures from 96 rats. We show representative examples of ictal and nonictal data as captured by our experimental paradigm in Figure 1. Our machine learning approach to train classifiers on these data is outlined Figure 1E.

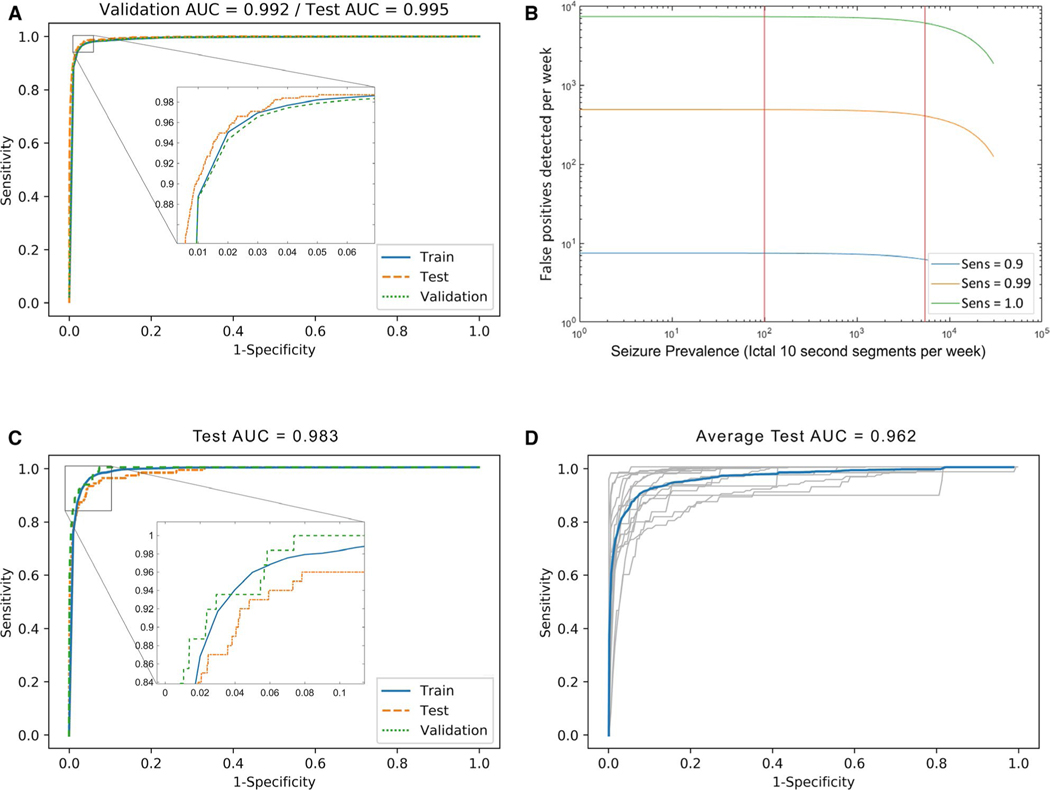
We first trained the classifier on data pooled among all subjects. As shown in Figure 2A, the pooled classifier achieved an AUROC of 0.995 on test data. At a sensitivity of 0.99, the classifier rendered a specificity of 0.911. Operating at this threshold with the mean seizure frequency of 13.5 seizures per week renders a mean positive predictive value (PPV) of 0.0074 for any positive 10-second window. The mean PPV for whether any positive minute contains a seizure is 0.015, and PPV for a positive hour is 0.49, calculated with the assumption that each seizure falls within a single minute or hour. Per Figure 2B, given multiple sensitivities in the range between 0.9 and 0.99 on the 95% confidence interval (CI) of prevalence in our data set, the weekly false discovery rate (FDR) is bounded between 6.2 and 487 false-detection events per week, based on the prevalence 95% confidence interval (CI). This weekly FDR yields the equivalent of an hourly FDR in the range between 0.0369 and 2.89 events/hour. The optimal hyperparameters from the grid search for the pooled classifier were lambda of 0.01 and 50 feature principal components (PCs). Figure 2C with an AUROC of 0.983 demonstrates comparable high performance for 24 hours of continuous testing data that is held out from and chronologically preceded by all the training data. As can be seen in Figure 2D, the mean AUROC of our extrapolated classifier, in which no data from the test subject were included in training, was 0.962. The optimal hyperparameters from a grid search conducted for each extrapolated classifier were a lambda in the range of 0.01 to 1 and retention in the range of 5 to 50 feature PCs with this regularization.

FIGURE 2.

Automated seizure-detection performance for the generalized linear model. For this analysis, 3054 ictal windows from 1012 seizures and 995 588 nonictal windows from the nonictal (interictal and preictal) segments were selected from 16 rats and pooled for this analysis. A, Method performance by receiver operating characteristic (ROC) curve for a pooled generalized linear model with ridge penalty, trained on 80% of all subject data pooled, and tested on the remaining hold-out 20% (test area under the curve [AUC] = 0.995). B, Performance visualized as false-positive seizures detected per week, at three sensitivity levels chosen for clinical relevance. Vertical red lines indicate boundaries of 95% confidence interval for seizure prevalence based on the Focal Epilepsy data set. C, Method performance by ROC for a pooled generalized linear model with ridge penalty, trained on 80% of all subject data, and tested on the held-out continuous last 24 h before the last recorded seizure, including the last seizure (test AUC = 0.983). D, Method performance by ROC for a generalized linear model with ridge penalty, trained on all data from all subjects except one, and tested on all data from the hold-out animal. ROC for each animal is shown in gray; mean ROC is shown in blue (mean test AUC = 0.962)

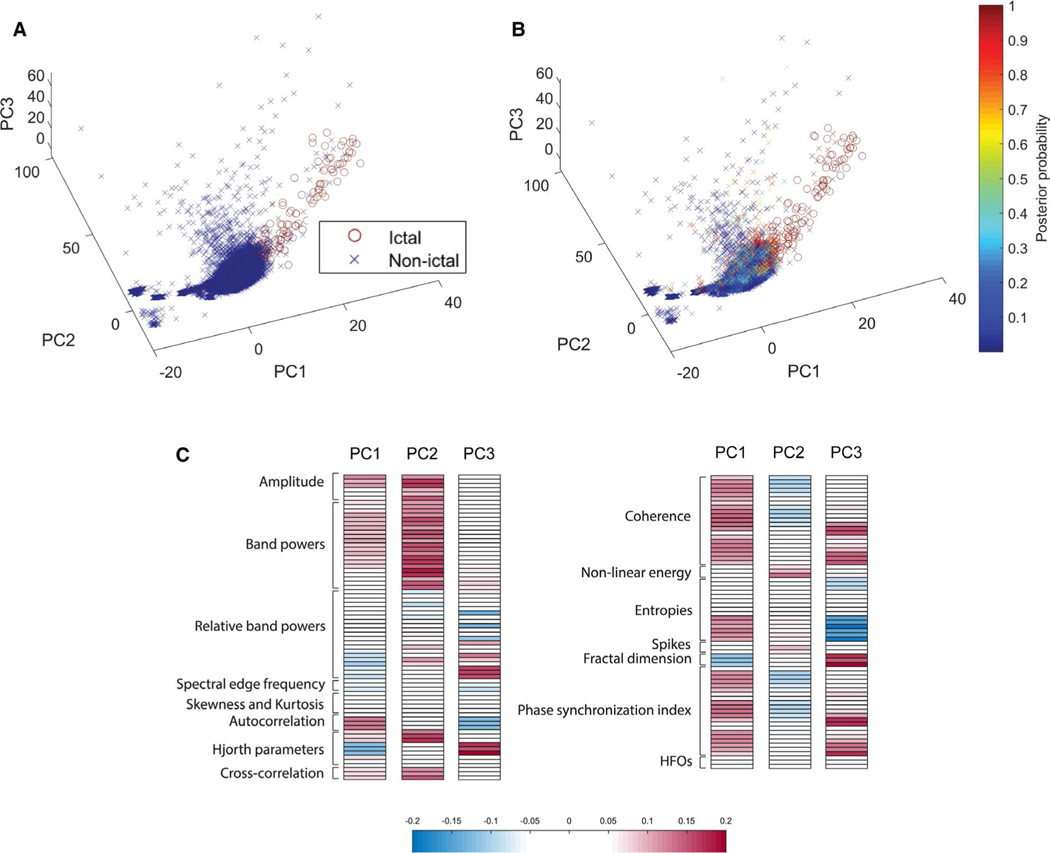
To visualize the class separability of ictal vs nonictal EEG in our highly correlated feature space, we applied a PCA to all features on a representative sample of the data. Figure 3A,B shows the data plotted on the first three PCs, with similar results for ground truth and for our classifier label, shown as a probability without thresholding. These PCA visualizations reflect the high degree of separability of ictal and nonictal EEG data along the axes constructed, both in the ground truth label and the classifier probabilistic label. This visualization validates the effective nature of the feature space in separating ictal and nonictal EEG data. Figure 3C plots the loadings of each feature in each of the first three PCs. The first PC highlights the importance of multi-channel features, that is, coherence and phase synchronization index, in explaining the variance of the data set. PC2 appears to correlate with features describing the amplitude of the signal, whereas PC3 corresponds generally to higher frequency features as well as other measures of the signal, such as entropies, Hjorth parameters, and fractal dimension.

FIGURE 3.

Ictal and nonictal electroencephalography (EEG) are highly separable in the principal component (PC) space. Principal component analysis (PCA) was performed on the EEG features described above for data pooled from four randomly selected animals. The EEG segments are then plotted in the space of the first three principal components. A, True classes of each data point in the testing set, where nonictal windows are represented by a blue cross and ictal windows by a red circle. B, Posterior probabilities superimposed as colors on crosses for nonictal windows, and circles for ictal windows. C, Loadings of each feature in the first three PCs, grouped by labeled feature class

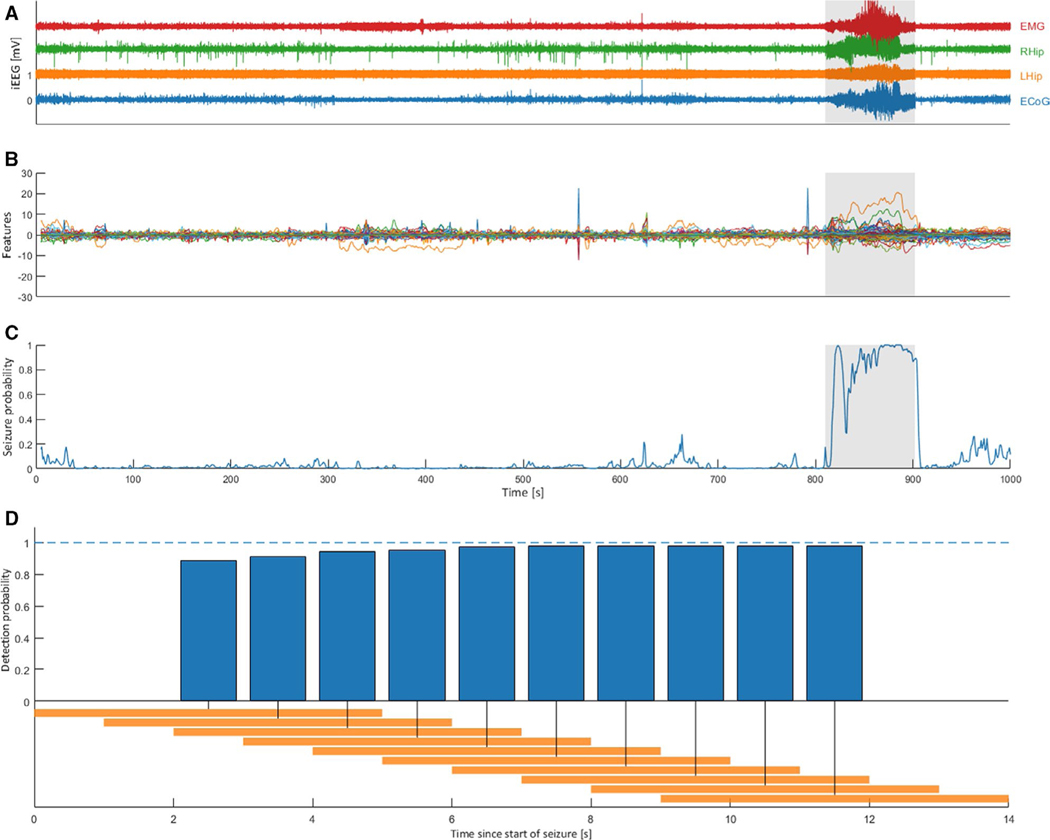
We sought to determine whether our model, in which the temporal order of ictal windows is indeterminate, continues to exhibit high levels of performance as an early seizure detector, such that it might be used for therapeutic interventions. The mean latency at the resolution of 5- second windows was under 5 seconds, as over 80% of seizures were detected within the first 5 seconds. For the representative sample seizure shown in Figure 4A, the overall seizure probability clearly increases specifically within the first 10 seconds of the labeled seizure, as indicated in Figure 4C. As observed in Figure 4B, certain PC features are specifically predictive of this particular seizure; the model combines them to detect the seizure with high probability per Figure 4C. As shown in Figure 4D, when thresholding for a seizure probability of 0.5, over 80% of seizures are detected within the first 5 seconds, and over 99% in the first 12 seconds.

FIGURE 4.

A generalized linear model classifier detects seizures with high specificity and low latency. The pooled classifier shows performance with latency under 5 seconds for over 80% of seizures, one representative sample of which is shown here. A, The electrographic plotted in time with the sample seizure segment highlighted in gray; x-axis matches (C). B, Standardized values for all PC features plotted in time with the sample seizure segment highlighted in gray; x-axis matches (C). C, Seizure probability computed by the model plotted in time. D, Cumulative latency histogram of sensitivity with a probability threshold of 0.5. Plotted is the cumulative proportion of events detected for 5-second windows (shown in orange on the timeline). Zero on the time axis represents the earliest timepoint labeled as seizure. This distribution is composed of 5-second windows overlapped by 80% to achieve 1-second resolution

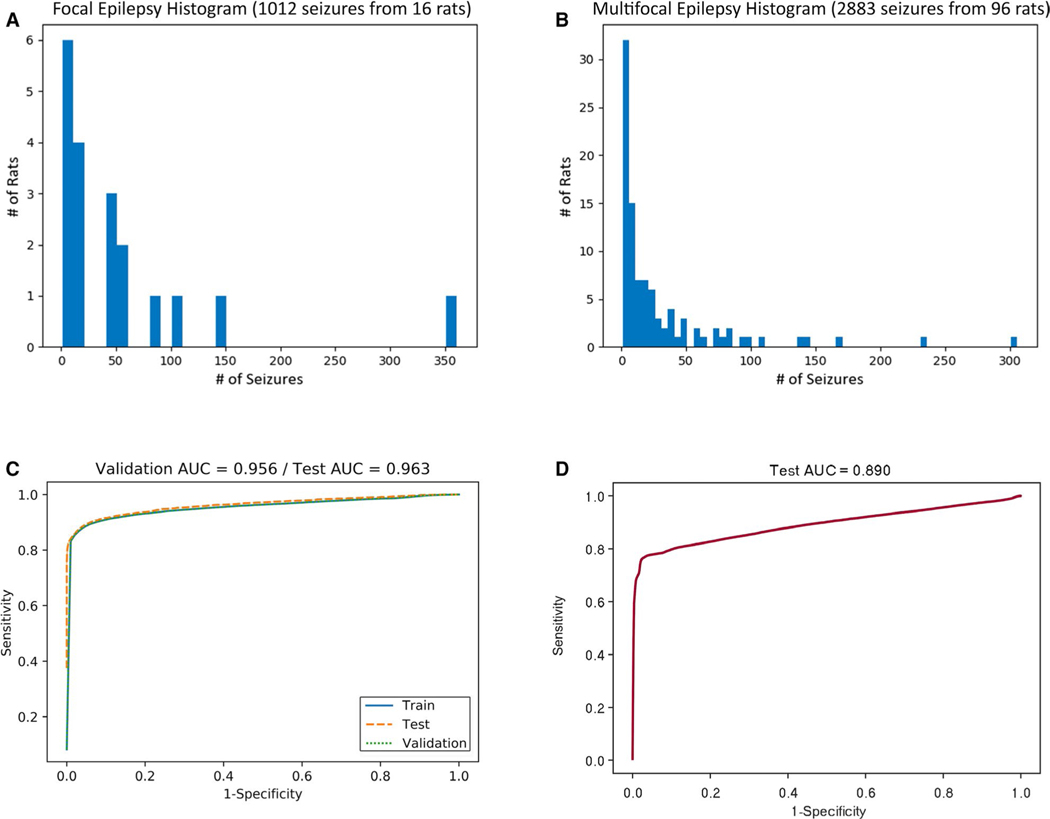
Having established the performance of the GLM on the Focal Epilepsy data set, we then sought to validate our method by applying it to the Multifocal Epilepsy data set, with related but distinct characteristics as reflected in Figure 5A,B. The mean and variance of seizure frequency was not significantly different by a t test (P = .089) and a Brown-Forsythe test (P = .12), respectively. Because the Multifocal Epilepsy data set contains only a single channel, we calculated the univariate subset of features from Table 1 (ie, excluding bivariate features like coherence and cross-correlation). We then applied the same grid search of hyperparameters to train multiple GLMs and obtain the highest performing one. The performance is displayed as an AUROC of 0.963 in Figure 5C. To assess the validity of individual models between data sets, we used the single ECoG channel data from the Focal Epilepsy data set to train a GLM using the univariate feature subset. We then tested the performance of that model in classifying the Multifocal Epilepsy data set, rendering an AUROC of 0.890 (Figure 5D).

FIGURE 5.

Application of detection method to large single-channel Multifocal Epilepsy data set. A, Seizure distribution of the Focal Epilepsy data set (1012 seizures from 16 rats, four-channel EEG). There was a mean of 54.0 ± 81.6 seizures per subject in the Focal Epilepsy data set. B, Seizure distribution of the Multifocal Epilepsy data set (2883 seizures from 96 rats, single-channel EEG). There was a mean of 30.0 ± 48.4 seizures per subject in the Multifocal Epilepsy data set. C, External validation of method with performance by ROC for a newly trained GLM with ridge penalty for the Multifocal Epilepsy data set. D, External validation of model with performance by ROC for GLM model trained on Focal Epilepsy data set, tested on the Multifocal Epilepsy data set

4 |. DISCUSSION

Our results suggest that a GLM trained on the features enumerated in Table 1 constitutes a robust method for the detection of seizures with low latency. Our pooled classifier performs at the current state of the art. As explored previously, Bose and colleagues reported an AUROC of 0.995 for a pooled classifier using a random forest method, which is a benchmark for the current state of the art.²¹ We have matched this performance with our pooled classifier AUROC of 0.995, as shown in Figure 2A, using a simpler method with more interpretable features and reduced computational complexity. Our model’s FDR is comparable to those of previous detectors being studied for clinical applications.^30,31 One caveat for our results is that the considerable variability between seizure patterns in human mTLE patients, let alone other etiologies, may differ from that in rodent models of focal epilepsy.^7,32 The continuous model demonstrates high performance also suitable for applications in both research and clinical settings. We hypothesize that the countinous model AUROC of 0.983 is lower than that of the pooled classifier due to additional variability in seizure phenotype as epilepsy progresses over time in a given animal.

In comparison to previous studies reliant on complex feature calculations, successful training of our model was contingent on the large number of labeled seizures. Although we optimized a pooled generalized model with 50 PCs computed from 141 features, these features are easily computable.

We anticipate that performance of the extrapolated classifier, in particular, may be further improved by inclusion of additional animals to fully exemplify focal seizure patterns. Data sets with hundreds of subjects consistently train classifiers with high performance for both pooled and extrapolated classifiers^{11,21,33–35} using both human and rodent EEG data. We observed lower performance for the GLM in the single-channel Multifocal Epilepsy data set (AUROC of 0.963), which we ascribe to less stereotyped seizure patterns than those found in unilateral focal seizures. We also hypothesize that using multiple channels to record those seizures would yield additional multichannel features that will improve performance to make it comparable to our pooled classifier. Therefore, our analyses of both the Focal Epilepsy and Multifocal Epilepsy data sets lend credence to the importance of bivariate features in seizure detection.

We have demonstrated the separability of ictal and nonictal classes via PCA to further illustrate the robust nature of the feature space. Being formulated in an unsupervised fashion without class labels, the first three principal components demonstrate the utility of the feature space itself. Just as the separability of ictal and nonictal segments is readily apparent in the visual representation of Figure 3, the GLM we trained can readily classify seizures with the high degree of accuracy reflected in Figure 2. As shown in Figure 4, our assessment of seizure detection latency rendered a distribution comparable to the state of the art, operating at higher specificity than the sub-second latency of clinical RNS systems.^1,9,31 Finally, we found that external validation of models between data sets is limited, as evidenced by the AUROC of 0.890 when training on Focal Epilepsy data, and testing on Multifocal Epilepsy data (Figure 5D). This limited performance suggests the relevance of the seizure type to highly accurate detection, particularly for multifocal seizures with data recorded on a single EEG channel. Nevertheless, such an externally trained model remains a viable starting point for automated preliminary seizure detection on a previously unanalyzed EEG data set.

Artifacts inherent in EEG data have often been cited as a significant barrier to classifier performance for seizure detection, as well as other machine learning applications.^4,18,36,37 In this study, intended to develop and test a method for seizure detection with real-world applications, we did not exclude EEG segments with artifact in either ictal or nonictal segments. Thus, our classifier will be robust to a real-world closed-loop application in which artifact will regularly be superimposed on both ictal and nonictal EEG data.

Ultimately, it remains to be seen whether the performance we observed in our data set will extrapolate to data from human patients with various epilepsies. Although we aimed to model mTLE with the intrahippocampal kainic acid rat model, which we selected for its low phenotypic variability, we recognize that many other human epilepsies are not as easily modeled in rats.⁸ However, the same approach described here could be used with a sufficiently large human data set to train a new model on human data with similar performance. One additional challenge in the clinical setting is the collection of sufficient high-quality recordings of seizures from each subject. Although we utilized 54.0 ± 81.6 seizures per subject in the Focal Epilepsy data set and 30.0 ± 48.4 seizures per subject in the Multifocal Epilepsy data set, in human patients, it is difficult to collect data from such a large number of seizures per subject with restrictive inpatient monitoring. With the increased availability of longer-term ambulatory recordings from implanted systems leading to larger sample sizes per patient, the clinical impact of seizure detection software such as ours will continue to grow.^38,39

An additional caveat is that we used all seizures, including and Racine 0 nonconvulsive electrographic seizures. Electrographic subclinical seizures were included to reduce bias for detector performance by maximizing variability of seizures represented, despite the attendant reduction in interrater agreement regarding the definition of a Racine 0 (nonconvulsive) electrographic seizure.⁴⁰ Detection of subclinical nonconvulsive seizures has clinical utility as well because of long-term effects on morbidity and mortality.⁴¹ However, this poses challenging questions as to the definition of the ground truth seizure for a detector to classify, particularly in the rat model, where immobile “seizure-like” states correlate with spike-wave discharges.⁴² These spike-wave discharges were frequently observed in our subjects. Because we were able to interrupt these events using tactile or auditory stimuli, they fell outside the scope of our definition of seizure, and thus we classified them as nonictal.⁴³

We envision multiple possible directions to build upon this analysis. First, this classifier can be used to implement a closed-loop interventional paradigm to assess seizure control. With an appropriate stimulatory paradigm, a significant reduction in seizure burden is expected.⁴⁴ Second, the classifier can be altered to be applied to data sets with different seizure characteristics, for example, extremely infrequent seizures, which requires more heavily weighting the seizure class. Finally, we foresee the use of this model as a broadly useful tool to label large data sets efficiently to rapidly enable other analyses, including for seizure prediction, seizure clustering, and investigating mechanisms of initiation. Such was the intention of testing the system on the Multifocal Epilepsy data set generated as part of the Epilepsy Therapy Screening Program (ETSP). We aim to eventually integrate this classifier into a fully automated seizure-prediction pipeline, wherein seizures are first automatically labeled, and then a predictive model is trained using those generated labels as ground truth.

In summary, our method automatically detected seizures in a preclinical epilepsy model with a high degree of sensitivity and specificity, with performance exceeding the current state of the art. This detection algorithm will significantly reduce the need to manually review EEG data to identify seizures, allowing the field to leverage larger EEG data sets from subjects with epilepsy to analyze seizure dynamics. In addition, it opens the door to a computationally simple method for low-power real-time detection of seizures for neuromodulatory intervention or for seizure forecasting and warning systems.

Key Points.

• Seizures can be automatically detected on electroencephalography (EEG) using a generalized linear model trained on a descriptive feature space

• Two independently constructed EEG data sets yielded models with high sensitivity and specificity, demonstrating the general validity of the method

• Latency to detection using this method is under 5 seconds for 80% of seizures

• This approach can be utilized to create large, accurately labeled EEG data sets for a seizure-prediction pipeline