Optimal Designs of Two-Phase Studies

Abstract

The two-phase design is a cost-effective sampling strategy to evaluate the effects of covariates on an outcome when certain covariates are too expensive to be measured on all study subjects. Under such a design, the outcome and inexpensive covariates are measured on all subjects in the first phase and the first-phase information is used to select subjects for measurements of expensive covariates in the second phase. Previous research on two-phase studies has focused largely on the inference procedures rather than the design aspects. We investigate the design efficiency of the two-phase study, as measured by the semiparametric efficiency bound for estimating the regression coefficients of expensive covariates. We consider general two-phase studies, where the outcome variable can be continuous, discrete, or censored, and the second-phase sampling can depend on the first-phase data in any manner. We develop optimal or approximately optimal two-phase designs, which can be substantially more efficient than the existing designs. We demonstrate the improvements of the new designs over the existing ones through extensive simulation studies and two large medical studies.

1. INTRODUCTION

In modern epidemiological and clinical studies, the outcomes of interest, such as disease occurrence and death, together with demographic factors and basic clinical variables, are typically known for all study subjects. The covariates of main interest often involve genotyping, biomarker assay, or medical imaging and thus are prohibitively expensive to be measured on all study subjects. A cost-effective solution is the two-phase design (White, 1982), under which the outcome and inexpensive covariates are observed on all subjects during the first phase and the first-phase information is used to select subjects for measurements of expensive covariates during the second phase. This type of design greatly reduces the cost associated with the collection of expensive covariate data and thus has been used widely in large-scale studies, including the National Wilms’ Tumor Study (Green et al., 2001; Warwick et al., 2010) and the National Heart, Lung, and Blood Institute Exome Sequencing Project (Lin et al., 2013).

A large body of literature exists on statistical inference for two-phase studies. For case-control studies, Prentice and Pyke (1979) showed that standard logistic regression ignoring the retrospective nature of the sampling scheme yields valid and efficient inference for the odds-ratio parameters. For designs under which every subject has a positive probability of being selected in the second phase, Robins et al. (1995) developed efficient estimators based on augmented inverse probability of selection weighting. For more general designs, Chatterjee et al. (2003) and Weaver and Zhou (2005) constructed inefficient estimators based on pseudo and estimated likelihood, respectively. Efficient estimators that are computationally feasible were proposed by Scott and Wild (1991), Breslow and Holubkov (1997), Scott and Wild (1997), Lawless et al. (1999), and Breslow et al. (2003) when the first-phase variables are discrete and by Song et al. (2009) and Lin et al. (2013) when there are no inexpensive covariates. Recently, Tao et al. (2017) studied efficient estimation under general two-phase designs, where the sampling in the second phase can depend on the first-phase data in any manner, and the outcome and inexpensive covariates can be continuous.

The design aspects of two-phase studies have received much less attention than the inference procedures. It is natural to ask which design leads to the most efficient inference on the effects of expensive covariates. The answer to this question is known only when there are no inexpensive covariates. Specifically, Prentice and Pyke (1979)’s work implies that the case-control design with an equal number of cases and controls is optimal. For a continuous outcome, Lin et al. (2013) showed that the two-phase design is more efficient if it selects subjects with more extreme values of the outcome variable.

The use of two-phase designs in large cohort studies with potentially censored event times has been a topic of great interest. Important examples include the case-cohort design (Prentice, 1986), which selects all cases and a random subcohort, and the nested case-control design (Thomas, 1977), which selects a small number of controls at each observed event time. These designs have been extended so as to select a fraction of, rather than all, cases (Cai and Zeng, 2007). Recently, Ding et al. (2014) proposed a general failure-time outcome-dependent sampling scheme that selects cases with extremely large or small observed event times in addition to a random subcohort, and Lawless (2018) suggested to select the smallest observed event times and the largest censored observations. Various methods have been developed to make inference under two-phase cohort studies; see Zeng and Lin (2014) and Ding et al. (2017) for reviews. However, no theoretical results exist on optimal cohort sampling.

Inexpensive covariates can be used in the second-phase sampling to enhance efficiency. For discrete outcomes, Breslow and Chatterjee (1999) stratified the second-phase sampling by the outcome and inexpensive covariates jointly. For continuous outcomes, the National Heart, Lung, and Blood Institute Exome Sequencing Project selected subjects with extreme values of the residuals from the linear regression of the outcome on inexpensive covariates (Lin et al., 2013). Zhou et al. (2014) proposed a probability-dependent sampling scheme, which selects a simple random sample at the beginning of the second phase and selects the remaining subjects using the predicted values of the expensive covariate. For censored outcomes, Borgan et al. (2000) stratified the selection of the subcohort in the case-cohort design on inexpensive covariates, and Langholz and Borgan (1995) used inexpensive covariates to select “counter-matched” controls at each observed event time. Whether any of the aforementioned two-phase designs are optimal among designs that make use of inexpensive covariates is unknown.

In this paper, we investigate the efficiency of general two-phase designs, where the second-phase sampling can depend on the first-phase data in any manner, and the outcome variable can be continuous, discrete, or censored. The design efficiency pertains to the semiparametric efficiency bound for estimating the regression coefficients of expensive covariates. We explore the optimal designs that maximize the efficiency among all possible two-phase designs and find good approximations to the optimal designs when they are not directly implementable. In addition, we compare the efficiencies of the proposed and existing two-phase designs through extensive simulation studies. Finally, we provide applications to the National Wilms’ Tumor Study and the National Heart, Lung, and Blood Institute Exome Sequencing Project.

2. THEORY AND METHODS

2.1. Data and Models

Let Y denote the outcome of interest, X the expensive covariate, and Z the vector of inexpensive covariates. The observation (Y X, Z) is assumed to be generated from the joint density p_θ,η(Y | X, Z) f (X, Z), where p_θ,η(·|·,·) pertains to a parametric or semiparametric regression model indexed by parameters θ = (α,β,γ^T)^T and η_,(α,β,γ) are the regression coefficients in the linear predictor μ(X,Z) = α + βX + γ^TZ, η is a possibly infinite-dimensional nuisance parameter, and f (·,·) is the joint density of X and Z with respect to a dominating measure. For linear regression,

$$p_{\mathit{\theta },\eta }(Y|X,\mathit{Z})={\left(2\pi {\sigma }^2\right)}^{-1/2}\text{exp}\left[-{\left\{Y-\mu (X,\mathit{Z})\right\}}^2/\left(2{\sigma }^2\right)\right],$$

Where η = σ²; for logistic regression,

$$p_{\mathit{\theta },\eta }(Y=1|X,\mathit{Z})={[1+\text{exp}\{-\mu (X,\mathit{Z})\}]}^{-1}.$$

For proportional hazards regression (Cox, 1972), the hazard function of the event time T conditional on covariates X and Z takes the form λ(t) exp{μ(X, Z)}, where α in μ(X, Z) is set to zero, and λ(·) is an unknown baseline hazard function, which corresponds to η. In the presence of right censoring, the observed outcome becomes $Y=(\tilde{T},\mathrm{\Delta })$, where $\tilde{T}=\text{min}(T,C)$, Δ = I (T ≤ C), C is the censoring time on T, and I(·) is the indicator function. Assuming that C is independent of T and X conditional on Z, we have

$$p_{\mathit{\theta },\eta }(Y|X,\mathit{Z})\propto {[\lambda (\tilde{T})\text{\hspace{0.17em}exp}\{\mu (X,\mathit{Z})\}]}^{\mathrm{\Delta }}\text{\hspace{0.17em}exp}[-\Lambda (\tilde{T})\text{\hspace{0.17em}exp}\{\mu (X,\mathit{Z})\}],$$

where $\Lambda (t)={\int }_0^t\lambda (u)du$.

2.2. Efficient Inference Under Two-Phase Sampling

If (Y,X, Z) is observed for all n subjects in the study, then the inference on θ is typically based on the likelihood $\prod _{n=1}^n{p}_{\mathit{\theta },n}\left(Y_i|X_i,{\mathit{Z}}_i\right)$. Under the two-phase design, however, only (Y, Z) is measured on all n subjects in the first phase, and X is measured for a sub-sample of size n₂ in the second phase. Let R be the selection indicator for the measurement of X in the second phase. It is assumed that the distribution of (R₁,…,R_n) depends on (Y_i,X_i,Z_i) (i = 1,…,n) only through the first-phase data (Y_i,Z_i) (i = 1,…,n). This assumption implies that the data on X are missing at random, such that the joint distribution of (R₁,…,R_n) conditional on (Y₁,Z₁,…,Y_n,Z_n) can be disregarded in the likelihood inference on _θ. Thus, the observed-data likelihood can be written as

$$L(\mathit{\theta },\eta ,f)=\prod _{i=1}^n{\left\{p_{\mathit{\theta },n}\left(Y_i|X_i,{\mathit{Z}}_i\right)f\left(X_i,{\mathit{Z}}_i\right)\right\}}^{R_i}{\left\{\int p_{\mathit{\theta },n}\left(Y_i|x,{\mathit{Z}}_i\right)f\left(x,{\mathit{Z}}_i\right)dx\right\}}^{1-R_i}.$$ (1)

Our main interest lies in the inference on β.

Remark 1. For designs that select a simple random sample at the beginning of the second phase, the observed-data likelihood (1) is valid even if the selection of the remaining subjects depends on the values of X in the simple random sample.

As mentioned in Section 1, efficient inference on β has been studied for different regression models (e.g., Robins et al., 1995; Breslow et al., 2003; Lin et al., 2013). In particular, nonparametric maximum likelihood estimation, under which the distribution of covariates is unspecified, has been developed by Tao et al. (2017) for continuous and discrete outcomes and by Zeng and Lin (2014) for censored data. Specifically, the joint density f (x, z) in (1) is expressed as the product of the marginal density of Z and the conditional density of X given Z = z. The marginal density of Z drops out of the likelihood, whereas the conditional density of X given z is estimated through sieves and kernel smoothing by Tao et al. (2017) and Zeng and Lin (2014), respectively. Under mild regularity conditions, the nonparametric maximum likelihood estimator for β, denoted by $\widehat{\beta }$, is consistent, and $n^{1/2}(\widehat{\beta }-\beta )$ is asymptotically zero-mean normal with a variance that attains the semiparametric efficiency bound. We denote this variance by V_β. By definition, the design is more efficient if the corresponding V_β is smaller, and the optimal design minimizes V_β for a given n₂.

2.3. Design Efficiency

In this subsection, we present some theoretical results on V_β in terms of the joint distribution of (Y,X,Z) and the probability of R = 1 given (Y,Z). The general form of V_β is available but involves an implicit integral equation (Robins et al., 1995; Bickel et al., 1998). To make the expression of V_β analytically tractable, we assume that β is small in the sense that β = o(1). This situation is of practical importance because design efficiency is the most critical when β is small, as in genetic association studies. For commonly used regression models, the information matrix is insensitive to perturbation in β, such that the expression of V_β under β = o(1) provides a good approximation for large β.

Let D_μ be the derivative of logp_θ,η (Y|X,Z) with respect to the linear predictor μ. We state below our main theoretical result.

Theorem 1. Under β = o(1),

$$V_{\beta }={\left[{\Sigma }_1+\text{E}\left\{R\text{\hspace{0.17em}var}\left(D_{\mu }|R=1,\mathit{Z}\right)\text{\hspace{0.17em}var}(X|\mathit{Z})\right\}\right]}^{-1},$$ (2)

Where Σ₁ is the Fisher information for β in the regression model p_θ,η (Y | X,Z) based on one observation, with X replaced by E(X | Z).

The proof of Theorem 1 is given in the Appendix. A key step in the proof is to derive the efficient score function for β using the semiparametric efficiency theory (Bickel et al., 1998) and the fact that Y and X are approximately independent given Z under β = o(1). When β = 0, Z is discrete, and η is finite-dimensional, taking the inverse of the two sides of equation (2) yields equation (7) in Derkach et al. (2015).

In Theorem 1, Σ₁ does not depend on R. Therefore, searching for the optimal, two-phase design is equivalent to finding the sampling rule R that maximizes

$$\text{E}\left\{R\text{\hspace{0.17em}var}\left(D_{\mu }|R=1,\mathit{Z}\right)\text{\hspace{0.17em}var}(X|\mathit{Z})\right\}$$ (3)

subject to the constraint

$$\text{Pr}(R=1)=\tau ,$$ (4)

where τ is the second-phase sampling fraction that is fixed by study budgets. In light of expression (3), it is desirable to select the subjects with the largest or smallest values of D_μ in each stratum of Z to maximize the variability of D_μ, where the strata correspond to the levels of discrete or discretized Z. In addition, expression (3) shows that the optimal design should oversample subjects with the largest values of var(X | Z). This is reasonable because X is harder to “impute” by Z when var(X | Z) is larger, such that measuring X among subjects with larger values of var(X | Z) is more “rewarding” than measuring X among subjects with smaller values of var(X | Z). We formalize these heuristic arguments in the following theorem, whose proof is provided in the Appendix.

Theorem 2. The optimal sampling rule R^opt under budget constraint (4) takes the following form:

$$\text{Pr}\left(R^{\text{opt}}=1|D_{\mu }=d_{\mu },\mathit{Z}=\mathit{z}\right)=\{\begin{array}{ll}1\hfill & \text{if }{d}_{\mu }<l_{\mathit{z}}\text{ or }{d}_{\mu }>u_{\mathit{z}},\hfill \\ a_{\mathit{z}}\hfill & \text{if }{d}_{\mu }=l_{\mathit{z}}\text{ and Pr}\left(D_{\mu }=l_{\mathit{z}}|\mathit{Z}=\mathit{z}\right)>0,\hfill \\ b_{\mathit{z}}\hfill & \text{if }{d}_{\mu }=u_{\mathit{z}}\text{ and Pr}\left(D_{\mu }=u_{\mathit{z}}|\mathit{Z}=\mathit{z}\right)>0,\hfill \\ 0\hfill & \text{othervise, }\hfill \end{array}$$ (5)

where (l_z,u_z,a_z,b_z) for each z in the support of Z is chosen to maximize

$${\int }_{\mathit{z}}[{\int }_{\left\{d_{\mu }<l_{\mathit{z}}\right\}\cup \left\{d_{\mu }>u_{\mathit{z}}\right\}}{d}_{\mu }^{2}dF\left(d_{\mu }|\mathit{z}\right)+l_{\mathit{z}}^2{a}_{\mathit{z}}F\left(\left\{l_{\mathit{z}}\right\}|\mathit{z}\right)+u_{\mathit{z}}^2{b}_{\mathit{z}}F\left(\left\{u_{\mathit{z}}\right\}|\mathit{z}\right)-\frac{{\left\{{\int }_{\left\{d_{\mu }<l_{\mathit{z}}\right\}\cup \left\{d_{\mu }>u_{\mathit{z}}\right\}}{d}_{\mu }dF\left(d_{\mu }|\mathit{z}\right)+l_{\mathit{z}}{a}_{\mathit{z}}F(\{l_{\mathit{z}}\}|\mathit{z})+u_{\mathit{z}}{b}_{\mathit{z}}F\left(\left\{u_{\mathit{z}}\right\}|\mathit{z}\right)\right\}}^2}{F\left(l_{\mathit{z}}^{-}|\mathit{z}\right)+1-F\left(u_{\mathit{z}}^{+}|\mathit{z})+a_{\mathit{z}}F\left(\left\{l_{\mathit{z}}\right\}|\mathit{z}\right)+b_{\mathit{z}}F(\{u_{\mathit{z}}\}|\mathit{z}\right)}]\text{\hspace{0.17em}var}(X|\mathit{z})d{F}_{\mathit{z}}(\mathit{z})$$ (6)

subject to

$$\int \left\{F\left(l_{\mathit{z}}^{-}|\mathit{z}\right)+1-F\left(u_{\mathit{z}}^{+}|\mathit{z}\right)+a_{\mathit{z}}F\left(\left\{l_{\mathit{z}}\right\}|\mathit{z}\right)+b_{\mathit{z}}F\left(\left\{u_{\mathit{z}}\right\}|\mathit{z}\right)\right\}d{F}_{\mathit{z}}(\mathit{z})=\tau .$$ (7)

Here, F_Z is the cumulative distribution function of Z, F(·| z) is the conditional cumulative distribution function of D_μ given Z = z, and F({d_μ}| z) is the jump size of F(d_μ | z) at D_{μ =} d_μ.

Remark 2. If F(·| z) is continuous, then a_z = b_z = 0, and equation (5) and expression (6) can be simplified greatly. Note that expression (6) and constraint (7) correspond to expression (3) and constraint (4), respectively.

Theorem 2 confirms that the optimal design selects subjects with the largest or smallest values of D_μ in each stratum of Z and favors the strata with the largest values of var(X | Z). Under β = 0, μ(X,Z) reduces to μ(Z) = γ^TZ. For linear regression, D_μ = {Y − μ(Z)}/σ², which is the error term scaled by σ²; for logistic regression D_μ = Y−[1 + exp{−μ(Z)}]⁻¹, which is the deviance for one subject; for proportional hazards regression, $D_{\mu }=\mathrm{\Delta }-\Lambda (\tilde{T})\text{\hspace{0.17em}exp}\{\mu (\mathit{Z})\}$, which is a martingale. The unknown parameters in D_μ are estimated by the first-phase data to yield the scaled, deviance, and martingale residuals for the linear, logistic, and proportional hazards regression, respectively.

The dependence of the optimal design on var(X | Z) is a new discovery. In practice, var(X | Z) is unknown and needs to be estimated from prior knowledge or historical data. Many two-phase studies, including the National Heart, Lung, and Blood Institute Exome Sequencing Project, select a simple random sample in the second phase, which can be used to study multiple outcomes or to explore the correct form of the model. We can estimate var(X | Z) from this subsample and then use the optimal rule R^opt to select the remaining subjects. The resulting design is optimal among those with a second-phase simple random sample of the same size.

Remark 3. A question naturally arises as to what the “optimal” size of the simple random sample is. A larger simple random sample will yield a more accurate estimate of var(X | Z) but entails more efficiency loss. If the spread of var(X | Z) is small across different values of Z, then it may be sensible to treat var(X | Z) as a constant and not select a simple random sample at all. If the spread of var(X | Z) is large, then one should select the smallest number of subjects that ensures an accurate estimate of var(X | Z). A rule of thumb is to group Z into five strata and select ten subjects in each stratum.

2.4. Algorithms for Finding the Optimal Design

According to Theorem 2, the optimal design is determined by the distribution of D_μ at the two extreme tails and the variability of X in each stratum of Z. Except for some special distributions of D_μ, there exists no explicit solution for (l_z, u_z, a_z, b_z). In this subsection, we first derive the optimal designs for linear and logistic regression, where simple solutions exist. We then propose a generic algorithm for finding an approximate solution to the optimal design for general regression models.

For linear regression, D_μ = −{Y – μ(Z)}/σ². Under β = o(1) the conditional distribution of Y given Z is continuous and symmetric about zero. In this situation, the optimal design has an explicit form, as given in the following corollary, whose proof is provided in the Appendix.

Corollary 1. The second-phase sampling rule $R_{\text{linear}}^{\text{opt }}$, defined as

$$R_{\text{linear}}^{\text{opt }}=\{\begin{array}{l}1\text{ if\hspace{0.17em}}{\{Y-\mu (\mathit{Z})\}}^2\text{\hspace{0.17em}var}(X|\mathit{Z})\ge c_0^2,\hfill \\ 0\text{ otherwise},\hfill \end{array}$$

where c₀ is chosen to satisfy $\text{Pr}\left[{\{Y-\mu (\mathit{Z})\}}^2\text{\hspace{0.17em}var}(X|\mathit{Z})\ge c_0^2\right]=\text{Pr}\left(R_{\text{linear}}^{\text{opt }}=1\right)=\tau$, maximizes expression (3) over all rules that satisfy budget constraint (4).

Corollary 1 sheds light on existing two-phase designs. If var(X | Z) is a constant, then the optimal design is the same as the residual-dependent sampling design that selects subjects with extreme values of Y – μ(Z). If we further assume that Z does not affect Y, such that μ(Z) is a constant, then the optimal design becomes the outcome-dependent sampling design that selects subjects with extreme values of Y; this result was previously proven by Lin et al. (2013). The probability-dependent sampling design of Zhou et al. (2014) requires a simple random sample at the beginning of the second phase; it selects the remaining subjects using the extreme predicted values of X, where the prediction model is built on the simple random sample. This sampling strategy essentially maximizes E{R var(X | Z,Y,R =1)}, which reduces to

$$\text{E}\{R\text{\hspace{0.17em}var}(X|\mathit{Z})\}$$ (8)

under β = 0. Unlike expression (3), expression (8) ignores var(D_μ | R = 1,Z) Thus, the probability-dependent sampling design is less efficient than the optimal design.

For logistic regression, D_μ = Y−[1 + exp{−μ(Z)}]⁻¹. Because the conditional distribution of Y given Z among subjects with R = 1 is Bernoulli, we have var(Y | R = 1,Z) = E(Y | R = 1,Z) {1 − E(Y | R = 1,Z)}. By Bayes’ theorem, E(Y | R = 1,Z) = E(R | Y = 1,Z)E(Y | Z)/ E(R | Z)_{. Thus, expression (}3_{) equals}

$$\text{E}\left[\frac{\text{E}(R|Y=1,\mathit{Z})\text{E}(Y|\mathit{Z})\{\text{E}(R|\mathit{Z})-\text{E}(R|Y=1,\mathit{Z})\text{E}(Y|\mathit{Z})\}}{\text{E}(R|\mathit{Z})}\text{\hspace{0.17em}var}(X|\mathit{Z})\right].$$ (9)

We derive the optimal design that maximizes expression (9) in the following corollary, whose proof is provided in the appendix.

Corollary 2. Assume, without loss of generality, that E(Y | Z) ≤1/2. The optimal sampling rule $R_{\text{logistic}}^{\text{opt }}$ satisfies

$$\text{E}\left(R_{\text{logistic}}^{\text{opt }}|Y=1,\mathit{Z}\right)=\text{min}\left\{\text{E}\left(R_{\text{logistic }}^{\text{opt }}|\mathit{Z}\right)/2\text{E}(Y|\mathit{Z}),1\right\},$$ (10)

where $\text{E}\left(R_{\text{logistic}}^{\text{one }}|\mathit{Z}\right)$ maximizes

$$\text{E}\left(\left[I\left\{\frac{\text{E}(R|\mathit{Z})}{\text{E}(Y|\mathit{Z})}\le 2\right\}\frac{\text{E}(R|\mathit{Z})}{4}+I\left\{\frac{\text{E}(R|\mathit{Z})}{\text{E}(Y|\mathit{Z})}>2\right\}\text{E}(Y|\mathit{Z})\left\{1-\frac{\text{E}(Y|\mathit{Z})}{\text{E}(R|\mathit{Z})}\right\}\right]\text{\hspace{0.17em}var}(X|\mathit{Z})\right)$$ (11)

over E(R | Z) subject to budget constraint (4). In particular, if var(X | Z) is a constant and τ ≤ 2E(Y), then there exists a design such that E(R | Z) ≤ 2E(Y | Z) and E(R | Y = 1,Z) = E(R | Z)/{2E(Y | Z)}. Moreover, any such design maximizes (11) and thus is optimal.

Remark 4. Equation (10) is equivalent to E(RY | Z) = E{R(1 − Y) | Z} if E(R | Z) ≤ 2E(Y | Z). Thus, the optimal design selects an equal number of cases and controls within the strata of Z for which E(R | Z) ≤ 2E(Y | Z) and selects all cases and more controls than cases for the other strata. If var(X | Z) is a constant and τ ≤ 2E(Y), then the optimal design always selects an equal number of cases and controls in each stratum of Z. In this situation, the stratum sizes are irrelevant to design efficiency. In other situations, we determine the optimal stratum sizes by maximizing the empirical version of expression (11) through grid search.

For more complex models such as the proportional hazards model, the conditional distribution of D_μ given Z is not symmetric. In this situation, (l_z, u_z, a_z, b_z) does not have an explicit form, and finding the optimal design relies on numerical maximization of the empirical version of expression (3). When the conditional distribution of D_μ given Z is not too skewed, we suggest to select an equal number of subjects at the two extreme tails of D_μ in each stratum of Z and then determine the optimal second-phase sample size of each stratum by maximizing the empirical version of expression (3) through grid search. This design is easy to implement and should provide a good approximation to the optimal design.

Remark 5. When there is no information about var(X | Z) at all, treating it as a constant will result in a design that is optimal among those with the same second-phase sample stratification. For linear regression, Corollary 1 shows that the optimal design does not need to stratify on Z. Then treating var(X | Z) as a constant reduces the optimal design to residual-dependent sampling, which is always more efficient than outcome-dependent sampling whether var(X | Z) is a constant or not. For logistic regression, treating var(X | Z) as a constant reduces the optimal design to stratified case-control sampling. In this situation, we do not know the optimal stratum sizes because var(D_μ | R = 1,Z) = 1/4 for any Z (provided that τ < 2E(Y)). If var(X | Z) is a constant, then the stratum sizes are irrelevant to design efficiency. If the spread of var(X | Z) is large, then stratified case-control sampling with equal stratum sizes can be more or less efficient than case-control sampling when the strata with larger values of var(X | Z) are less or more prevalent than the other strata, respectively. For more complex models, such as the proportional hazards model, treating var(X | Z) as a constant is appropriate when the spread of var(X | Z) is small or when var(X | Z) and var(D_μ | R =1,Z) are positively correlated. Treating var(X | Z) as a constant can reduce design efficiency when the spread of var(X | Z) is large and var(X | Z) and var(D_μ | R = 1,Z) are negatively correlated.

3. SIMULATION STUDIES

We conducted extensive simulation studies to compare the efficiencies of various two-phase designs in realistic settings. In the first set of studies, we considered a continuous outcome with discrete covariates. Specifically, we set Z and X | Z to Bern(0.5) and Bern{I(Z = 0)p₀ + I(Z = 1)p₁}, respectively, with 0 < p₀ <1 and 0 < p₁ <1. We generated the outcome from the linear model Y =βX + γZ + ϵ₁, where ϵ₁ is a standard normal random variable independent of X and Z. We set n = 4000 and considered four sampling strategies at the second phase: simple random sampling selects 400 subjects randomly; outcome-dependent sampling selects 200 subjects with the highest and 200 subjects with the lowest values of Y; residual-dependent sampling selects 200 subjects with the highest and 200 subjects with the lowest values of $Y-\widehat{\mu }(Z)$, where $\widehat{\mu }(Z)=\widehat{\alpha }+\widehat{\gamma }Z$, and $\widehat{\alpha }$ and $\widehat{\gamma }$ are the least-squares estimates from the linear regression of Y on Z; and optimal sampling selects 200 subjects with the highest and 200 subjects with the lowest values of $\{Y-\widehat{\mu }(Z)\}{\{\text{\hspace{0.17em}var}(X|Z)\}}^{12}$, where var(X | Z = j) = p_j (1 − p_j) (j = 0,1). We performed maximum likelihood estimation (Tao et al., 2017) under the four designs. We evaluated the efficiency of each design according to the empirical variance of $\widehat{\beta }$. In addition, we compared the analytical variance V_β given in Theorem 1 with the empirical variance.

The results for the first set of studies are shown in Table 1 and Supplementary Table S1. We see that outcome-dependent, residual-dependent, and optimal sampling are much more efficient than simple random sampling. When γ = 0, residual-dependent sampling is as efficient as outcome-dependent sampling. When γ ≠ 0, residual-dependent sampling is more efficient than outcome-dependent sampling, and the efficiency gain increases as γ increases. When var(X | Z) is a constant, the optimal design is as efficient as residual-dependent sampling. When var(X | Z) is a non-trivial function of Z, the optimal design is substantially more efficient than residual-dependent sampling. The analytical standard error of $\widehat{\beta }$ approximates the empirical standard error very well when β is small. The approximation becomes less accurate when β is large; however, the bias tends to be small (relative to the true value) and in the same direction for different designs, such that the ordering of the design efficiencies is unaltered.

Table 1.

Simulation Results for Linear Regression With Discrete Covariates

				Analytical				Empirical				Efficiency
				standard error of $\widehat{\beta }$				standard error of $\widehat{\beta }$				relative to SRS
p0	p1	β	γ	SRS	ODS	RDS	OPT	SRS	ODS	RDS	OPT	ODS	RDS	OPT
0.7	0.7	0.0	0.0	0.109	0.052	0.052	0.052	0.109	0.053	0.053	0.053	4.23	4.24	4.24
			0.5	0.109	0.058	0.052	0.052	0.109	0.058	0.053	0.053	3.53	4.24	4.24
			1.0	0.109	0.080	0.052	0.052	0.109	0.081	0.053	0.053	1.83	4.24	4.24
		0.3	0.0	0.108	0.052	0.052	0.052	0.108	0.054	0.054	0.054	3.96	3.95	3.95
			0.5	0.108	0.057	0.052	0.052	0.108	0.060	0.054	0.054	3.21	3.95	3.95
			1.0	0.108	0.078	0.052	0.052	0.108	0.082	0.054	0.054	1.71	3.95	3.95
		0.5	0.0	0.107	0.051	0.051	0.051	0.104	0.057	0.057	0.057	3.31	3.31	3.31
			0.5	0.107	0.056	0.051	0.051	0.104	0.062	0.057	0.057	2.77	3.31	3.31
			1.0	0.107	0.076	0.051	0.051	0.104	0.083	0.057	0.057	1.55	3.31	3.31
0.5	0.9	0.0	0.0	0.122	0.058	0.058	0.055	0.122	0.059	0.058	0.055	4.35	4.37	5.01
			0.5	0.122	0.064	0.058	0.055	0.122	0.065	0.058	0.055	3.50	4.37	5.01
			1.0	0.122	0.089	0.058	0.055	0.122	0.090	0.058	0.055	1.82	4.37	5.01
		0.3	0.0	0.120	0.058	0.057	0.054	0.117	0.059	0.060	0.055	3.89	3.87	4.51
			0.5	0.120	0.067	0.057	0.054	0.117	0.068	0.060	0.055	3.02	3.87	4.51
			1.0	0.120	0.096	0.057	0.054	0.117	0.095	0.060	0.055	1.53	3.87	4.51
		0.5	0.0	0.119	0.057	0.056	0.053	0.110	0.061	0.061	0.056	3.19	3.23	3.82
			0.5	0.119	0.068	0.056	0.053	0.110	0.070	0.061	0.056	2.45	3.23	3.82
			1.0	0.119	0.099	0.056	0.053	0.110	0.097	0.061	0.056	1.29	3.23	3.82
0.1	0.5	0.0	0.0	0.122	0.058	0.058	0.055	0.123	0.059	0.059	0.055	4.36	4.36	5.00
			0.5	0.122	0.064	0.058	0.055	0.123	0.066	0.059	0.055	3.52	4.36	5.00
			1.0	0.122	0.088	0.058	0.055	0.123	0.091	0.059	0.055	1.82	4.36	5.00
		0.3	0.0	0.120	0.058	0.05	0.054	0.118	0.060	0.060	0.056	3.88	3.87	4.40
			0.5	0.12	0.067	0.057	0.054	0.118	0.068	0.060	0.056	3.03	3.87	4.40
			1.0	0.120	0.096	0.057	0.054	0.118	0.096	0.060	0.056	1.52	3.87	4.40
		0.	0.	0.11	0.05	0.05	0.05	0.11	0.06	0.06	0.05	3.18	3.19	3.72
		5	0	9	7	6	3	0	2	2	7
			0.5	0.119	0.068	0.056	0.053	0.110	0.071	0.062	0.057	2.43	3.19	3.72
			1.0	0.119	0.099	0.056	0.053	0.110	0.097	0.062	0.057	1.28	3.19	3.72

NOTE: SRS, ODS, RDS, and OPT denote simple random sampling, outcome-dependent sampling, residual-dependent sampling, and optimal design, respectively. Each entry is based on 10,000 replicates.

In the second set of simulation studies, we considered a continuous instead of a discrete expensive covariate. Specifically, we set X = 0.2Z + (1 + kZ)^1/2ϵ₂, where ϵ₂ is a standard normal random variable independent of Z and ϵ₁, and κ is a parameter that controls the value of var(X | Z). We set Z to Bern(0.5) or Unif(0,1). In addition to the two-phase designs considered in the first set of studies, we included four designs that select a simple random sample of 200 subjects at the beginning of the second phase. The following strategies were adopted to select the remaining 200 subjects in the second phase: outcome-dependent sampling selects subjects with extreme values of Y; residual-dependent sampling selects subjects with extreme values of $Y-\widehat{\mu }(Z)$; probability-dependent sampling (Zhou et al., 2014) selects subjects with extreme values of $\widehat{X}$, where $\widehat{X}$ is the predicted value of X from the linear regression of X on Y stratified by Z when Z is discrete and from the linear regression of X on (Y, Z) when Z is continuous; and optimal sampling selects subjects with extreme values of $\left\{Y-\widehat{\mu }(Z)\right\}{\left\{\text{\hspace{0.17em}var}(X|Z)\right\}}^{1/2}$, where var(X | Z) is estimated from the simple random sample.

The results for the second set of studies are summarized in Table 2 and Supplementary Tables S2–S3. In general, the designs that do not require a simple random sample at the beginning of the second phase are more efficient than those that do. Among designs that contain a simple random sample, the design that adopts the optimal sampling rule $R_{\text{linear}}^{\text{opt }}$ to select the remaining subjects in the second phase is the most efficient.

Table 2.

Relative Efficiencies of Two-Phase Designs to Simple Random Sampling for Linear Regression With a Continuous Expensive Covariate

				Without a simple			With a simple
				random sample			random sample
Z	κ	β	γ	ODS	RDS	OPT	ODS	RDS	PDS	OPT
Bern(0.5)	0.0	0.0	0.0	4.41	4.40	4.40	3.24	3.24	2.44	3.22
			0.5	3.55	4.40	4.40	2.82	3.24	2.44	3.22
			1.0	1.88	4.40	4.40	2.12	3.24	2.44	3.22
		0.3	0.0	2.57	2.60	2.60	2.29	2.30	1.93	2.28
			0.5	2.14	2.60	2.60	2.08	2.30	1.93	2.28
			1.0	1.37	2.60	2.60	1.74	2.30	1.93	2.28
		0.5	0.0	1.30	1.30	1.30	1.48	1.49	1.41	1.48
			0.5	1.12	1.30	1.30	1.42	1.49	1.41	1.48
			1.0	0.85	1.30	1.30	1.32	1.49	1.41	1.48
	−0.7	0.0	0.0	4.40	4.40	5.07	3.26	3.26	2.52	3.83
			0.5	3.55	4.40	5.07	2.83	3.26	2.52	3.83
			1.0	1.88	4.40	5.07	2.13	3.26	2.52	3.83
		0.3	0.0	2.48	2.49	2.90	2.14	2.15	2.01	2.35
			0.5	2.08	2.49	2.90	1.93	2.15	2.01	2.35
			1.0	1.35	2.49	2.90	1.63	2.15	2.01	2.35
		0.5	0.0	1.41	1.41	1.65	1.45	1.46	1.41	1.46
			0.5	1.20	1.41	1.65	1.36	1.46	1.41	1.46
			1.0	0.89	1.41	1.65	1.23	1.46	1.41	1.46
Unif(0, 1)	0.0	0.0	0.0	4.93	4.94	4.94	3.57	3.56	2.00	3.56
			0.5	4.61	4.93	4.93	3.38	3.55	2.00	3.55
			1.0	3.69	4.94	4.94	2.99	3.55	2.00	3.55
		0.3	0.0	2.82	2.83	2.83	2.50	2.50	2.01	2.50
			0.5	2.65	2.83	2.83	2.41	2.51	2.02	2.51
			1.0	2.26	2.83	2.83	2.22	2.51	2.01	2.51
		0.5	0.0	1.36	1.36	1.36	1.58	1.57	1.51	1.57
			0.5	1.30	1.36	1.36	1.54	1.57	1.50	1.57
			1.0	1.16	1.36	1.36	1.48	1.57	1.50	1.57
	−0.7	0.0	0.0	4.92	4.92	5.06	3.57	3.56	1.85	3.79
			0.5	4.60	4.92	5.06	3.38	3.56	1.86	3.79
			1.0	3.69	4.92	5.06	2.99	3.56	1.85	3.79
		0.3	0.0	3.18	3.21	3.40	2.68	2.67	1.86	2.77
			0.5	2.99	3.20	3.39	2.55	2.67	1.86	2.76
			1.0	2.55	3.21	3.39	2.36	2.67	1.86	2.76
		0.5	0.0	1.82	1.82	1.96	1.86	1.86	1.69	1.85
			0.5	1.72	1.82	1.96	1.81	1.86	1.69	1.85
			1.0	1.52	1.82	1.96	1.71	1.86	1.69	1.85

NOTE: ODS, RDS, PDS, and OPT denote outcome-dependent sampling, residual-dependent sampling, probability-dependent sampling, and optimal design, respectively. Each entry is based on 10,000 replicates.

In the third set of simulation studies, we considered a binary outcome. We generated X and Z in the same manner as in the first set of studies, except that we considered different values of E(Z). We simulated the outcome from the logistic model logit {Pr(Y = 1 | X,Z)} = a + βX + γZ, where we used α to control E(Y). We considered both common and rare outcomes. For a common outcome, we let E(Y) = 0.3 and varied E(Z) from 0.3 to 0.7. We set n = 10, 000 and defined two strata according to the values of Z. We set n₂ = 400 and compared the optimal design with case-control sampling, which selected 200 cases and 200 controls, and stratified case-control sampling, which selected 100 cases and 100 controls from each stratum. For a rare outcome, we set n = 4000, E(Y) = 0.14, and E(Z) = 0.1, mimicking the “rare disease and rare exposure” scenario described in Breslow and Chatterjee (1999). We compared the optimal design with case-control sampling and stratified case-control sampling, both of which select all cases and an equal number of controls in the second phase.

The results for the third set of studies are summarized in Table 3 and Supplementary Tables S4–S5. When var(X | Z) is a constant and γ = 0, all designs are equally efficient. When γ ≠ 0, stratified case-control sampling and optimal design are more efficient than case-control sampling, and the efficiency gain increases as γ increases. In addition, the similar efficiencies between stratified case-control sampling and optimal design confirm that the stratum size is irrelevant to the design efficiency. When var(X | Z) is a non-trivial function of Z, the optimal design is substantially more efficient than the other two designs. Stratified case-control sampling can be less efficient than case-control sampling when var(X | Z) is larger in the more prevalent stratum. These results disprove the common belief that it is always desirable to pursue an equal number of subjects per stratum.

Table 3.

Relative Efficiencies of Other Two-Phase Designs to Case-Control Sampling for Logistic Regression

				Common disease						Rare disease
				E(Z) = 0.3		E(Z) = 0.5		E(Z) = 0.7		E(Z) = 0.1
p0	p1	β	γ	SCC	OPT	SCC	OPT	SCC	OPT	SCC	OPT
0.7	0.7	0.0	0	0.98	1.00	1.03	1.04	0.97	1.00	0.99	0.98
			1	1.04	1.05	1.08	1.10	1.03	1.07	1.05	1.05
			2	1.23	1.27	1.30	1.29	1.18	1.19	1.17	1.17
		0.3	0	0.96	1.01	1.04	1.05	0.97	1.00	1.01	1.03
			1	1.04	1.07	1.09	1.07	1.05	1.03	1.06	1.05
			2	1.24	1.28	1.22	1.26	1.17	1.19	1.18	1.19
		0.5	0	0.99	1.01	1.02	1.00	1.01	1.04	1.01	0.99
			1	1.08	1.10	1.05	1.07	1.04	1.07	1.05	1.03
			2	1.28	1.33	1.23	1.26	1.13	1.15	1.14	1.12
0.5	0.9	0.0	0	0.84	1.20	1.02	1.45	1.25	1.77	0.97	1.02
			1	0.90	1.29	1.15	1.66	1.44	2.04	0.99	1.10
			2	1.10	1.64	1.56	2.18	1.71	2.51	0.95	1.10
		0.3	0	0.83	1.19	1.00	1.47	1.27	1.85	0.97	1.05
			1	0.91	1.31	1.16	1.65	1.45	2.08	0.99	1.08
			2	1.11	1.56	1.52	2.17	1.82	2.62	0.96	1.10
		0.5	0	0.82	1.23	1.02	1.50	1.29	1.95	1.01	1.06
			1	0.92	1.31	1.14	1.72	1.47	2.16	0.98	1.07
			2	1.12	1.58	1.57	2.18	1.86	2.75	0.96	1.09
0.1	0.5	0.0	0	1.22	1.80	0.98	1.46	0.85	1.21	1.01	1.02
			1	1.29	1.90	0.99	1.47	0.86	1.22	1.16	1.22
			2	1.52	2.10	1.12	1.58	0.90	1.28	1.55	1.56
		0.3	0	1.20	1.73	1.01	1.46	0.84	1.20	1.01	1.04
			1	1.29	1.84	1.01	1.41	0.84	1.17	1.16	1.24
			2	1.58	2.19	1.10	1.58	0.87	1.23	1.46	1.50
		0.5	0	1.22	1.74	0.98	1.37	0.84	1.16	1.02	1.06
			1	1.27	1.80	1.00	1.41	0.87	1.20	1.16	1.23
			2	1.53	2.11	1.16	1.58	0.89	1.23	1.41	1.43

NOTE: SCC and OPT denote stratified case-control sampling and optimal design, respectively. Each entry is based on 10,000 replicates.

In the last set of simulation studies, we considered a potentially censored event time. We generated X and Z in the same manner as in the first set of studies. We generated T from the Weibull proportional hazards model with cumulative hazard function 0.1t^0.7 exp(βX + γZ). In addition, we generated the censoring time C from a Uniform(0,c₁) distribution, where c₁ = 1or 5, yielding 85% to 94% or 64% to 84% censoring, to be referred to as high and moderate censoring rates, respectively. We set the cohort size n = 2000. In the case of moderate censoring rate, we set n₂ = 400 and compared the optimal design with four sampling strategies that select a subset of cases: case-cohort sampling (Cai and Zeng, 2007) selects 200 cases and 200 controls; stratified case-cohort sampling (Borgan et al., 2000) selects 100 cases and 100 controls from each of the two strata; general failure-time outcome-dependent sampling (Ding et al., 2014) selects 100 cases with the largest and 100 cases with the smallest observed event times in addition to a subcohort of 200 subjects; and Y-dependent sampling (Lawless, 2018) selects the 200 smallest observed event times and the 200 largest censored observations. In the case of high censoring rate, we compared the optimal design with four sampling strategies that select all cases and an equal number of controls in the second phase: case-cohort sampling (Prentice, 1986); stratified case-cohort sampling; nested case-control sampling (Thomas, 1977) with one control for each observed event time; counter-matching (Langholz and Borgan, 1995), which selects one control with Z = 0 for each case with Z = 1 and vice versa; and Y-dependent sampling.

The results for the last set of studies are summarized in Table 4 and Supplementary Tables S6–S7. The optimal design is much more efficient than the other designs in most situations. The Y-dependent sampling design is as efficient as the optimal design when var(X | Z) is a constant and γ = 0. In this situation, $D_{\mu }=\mathrm{\Delta }-\Lambda (\tilde{T})$, which is a monotone function of $\tilde{T}$. Therefore, selecting the smallest observed event times and the largest censored observations is equivalent to selecting subjects with the largest and smallest values of D_μ, respectively.

Table 4.

Relative Efficiencies of Other Two-Phase Designs to Case-Cohort Sampling Under the Proportional Hazards Model

				High censoring rate					Moderate censoring rate
p0	p1	β	γ	SCC	NCC	CM	YDS	OPT	SCC	ODS	YDS	OPT
0.7	0.7	0.0	0.0	1.01	1.01	0.97	1.06	1.07	1.02	0.99	1.35	1.36
			0.5	1.02	1.02	0.95	1.08	1.12	1.02	1.01	1.44	1.50
			1.0	1.11	1.07	0.90	1.17	1.28	1.07	1.01	1.58	1.94
		0.3	0.0	1.02	1.02	1.00	1.09	1.10	1.00	1.00	1.38	1.41
			0.5	1.05	1.03	0.98	1.13	1.16	1.02	1.00	1.50	1.56
			1.0	1.06	1.04	0.87	1.12	1.23	1.02	0.98	1.62	2.00
		0.5	0.0	1.00	1.03	1.02	1.11	1.11	1.01	0.98	1.43	1.43
			0.5	1.01	1.02	0.97	1.11	1.14	0.99	0.93	1.52	1.60
			1.0	1.03	1.03	0.90	1.14	1.24	1.04	0.93	1.65	2.05
0.5	0.9	0.0	0.0	0.99	1.03	1.04	1.08	1.18	0.99	0.97	1.34	1.62
			0.5	0.96	1.03	1.03	1.09	1.13	1.05	0.97	1.39	1.69
			1.0	0.96	1.03	0.99	1.12	1.15	1.13	0.99	1.50	1.82
		0.3	0.0	0.97	1.02	1.02	1.08	1.17	1.02	0.98	1.37	1.74
			0.5	0.95	1.05	1.07	1.14	1.14	1.10	1.00	1.48	1.87
			1.0	0.95	1.04	1.01	1.15	1.15	1.13	0.95	1.50	1.84
		0.5	0.0	0.98	1.01	1.05	1.11	1.17	1.07	0.98	1.45	1.90
			0.5	0.93	1.04	1.05	1.12	1.12	1.13	0.98	1.51	1.99
			1.0	0.93	1.02	0.98	1.14	1.12	1.17	0.94	1.51	1.89
0.1	0.5	0.0	0.0	0.97	1.01	0.99	1.06	1.14	0.99	0.95	1.30	1.56
			0.5	1.06	1.02	0.93	1.09	1.26	0.98	0.94	1.46	1.86
			1.0	1.22	1.06	0.82	1.15	1.43	0.96	0.93	1.63	2.33
		0.3	0.0	1.01	0.99	0.98	1.06	1.13	1.02	0.96	1.38	1.62
			0.5	1.06	1.05	0.92	1.09	1.26	0.98	0.90	1.49	1.90
			1.0	1.19	1.05	0.81	1.17	1.43	1.01	0.94	1.78	2.50
		0.5	0.0	1.03	1.03	1.02	1.10	1.17	0.96	0.93	1.40	1.61
			0.5	1.10	1.05	0.94	1.14	1.28	1.00	0.91	1.58	2.00
			1.0	1.17	1.07	0.81	1.18	1.44	1.00	0.92	1.73	2.43

NOTE: SCC, NCC, CM, ODS, YDS, and OPT denote stratified case-cohort sampling, nested case-control sampling, counter-matching, general failure-time outcome-dependent sampling, Y-dependent sampling, and optimal design, respectively. Each entry is based on 10,000 replicates.

4. APPLICATIONS

4.1. National Heart, Lung, and Blood Institute Exome Sequencing Project

The National Heart, Lung, and Blood Institute Exome Sequencing Project was designed to identify genetic variants in all protein–coding regions of the human genome that are associated with heart, lung, and blood disorders. The project performed whole-exome sequencing on 4494 subjects from seven large cohorts and consisted of several studies, each focusing on a particular outcome (Lin et al., 2013). The majority of the studies adopted two-phase designs. For example, the study on body mass index selected 659 subjects with body mass index less than 25kg / m² or greater than 40kg / m². The study on blood pressure selected 806 subjects from the upper and lower 0.2% to 1.0% of the blood pressure distribution adjusted for age, gender, race, body mass index, and anti-hypertensive medication. The study on low-density lipoprotein cholesterol selected 657 subjects with extremely high or low values of low-density lipoprotein cholesterol adjusted for age, gender, race, and lipid medication. In addition to the two-phase studies, the project obtained a simple random sample of 964 subjects with measurements on a common set of phenotypes, referred to as the “deeply phenotyped reference”. We used this deeply phenotyped reference to evaluate the efficiencies of two-phase designs.

We considered log-transformed body mass index as the outcome of interest and included age, gender, race, and cohort indicators as inexpensive covariates. We restricted our analysis to the 43,245 single-nucleotide polymorphisms (SNPs) with minor allele frequencies greater than 5%. We chose the additive genetic model, under which the genetic variable codes the number of minor alleles that a subject carries at a variant site. We set n² = 300 and considered three sampling strategies: outcome-dependent sampling; residual-dependent sampling; and optimal sampling. The probability-dependent sampling design (Zhou et al., 2014) is not applicable because it does not allow discrete expensive covariates. Because age, gender, and cohort indicators are independent of SNPs, we only need to estimate the conditional variance of the genetic variable given race when implementing the optimal design. Because this conditional variance depends on the genetic variable, the optimal sampling rule is specific to each SNP.

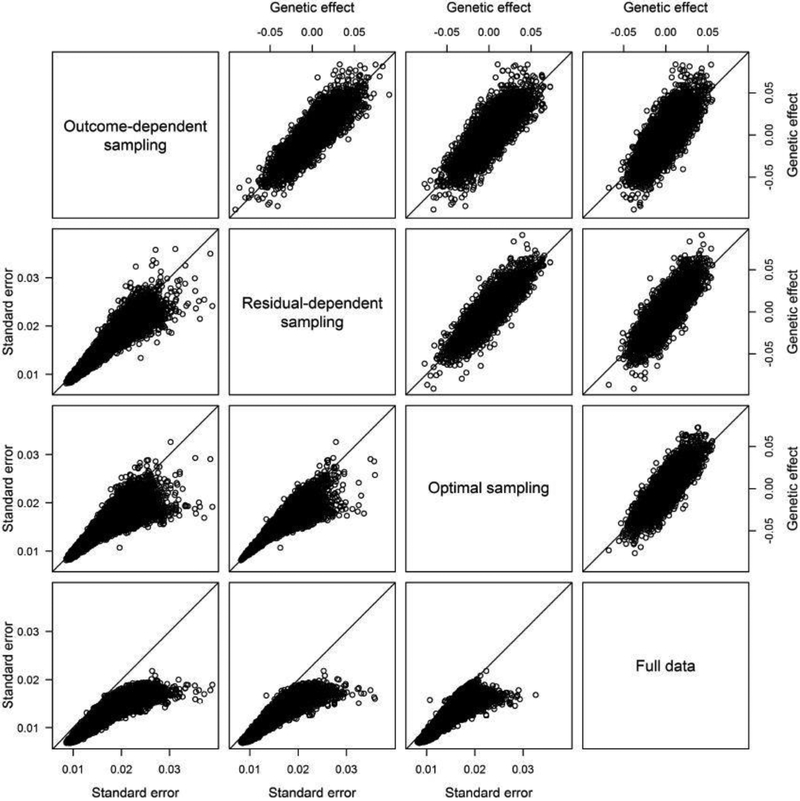
Figure 1 compares the estimates of the genetic effects and the standard error estimates among the three two-phase designs and the full-data analysis. The effect estimates are similar among the three two-phase designs and are close to those of the full-data analysis. The standard error estimates under the optimal design tend to be smaller than those under residual-dependent sampling, which tend to be smaller than those under outcome-dependent sampling. These results show that residual-dependent sampling can yield more precise genetic effect estimates and higher power than outcome-dependent sampling for genome-wide association studies, and the optimal design can be more efficient than residual-dependent sampling for candidate-gene studies.

Fig. 1.

Estimates of the genetic effects, shown in the upper right triangle, and standard errors, shown in the lower left triangle, from the linear regression of the log-transformed body mass index on SNPs in the deeply phenotyped reference for the National Heart, Lung, and Blood Institute Exome Sequencing Project.

4.1. National Wilms’ Tumor Study

The National Wilms’ Tumor Study Group conducted a series of studies on Wilms’ tumor, which is a rare childhood kidney cancer. We used data on 4028 patients from the group’s third and fourth clinical trials (D’angio et al., 1989; Green et al., 1998) to evaluate the effects of tumor histological type, stage, and age at diagnosis on disease relapse. The censoring rate was approximately 86%. This dataset was analyzed previously by Breslow and Chatterjee (1999).

Each tumor’s histological type was assessed by both a local pathologist and an experienced pathologist from a central facility. The latter assessment tends to be more accurate but is more expensive and time-consuming. If a two-phase design had been adopted to assess histological type at the central facility for only a small subset of patients, then the cost of the trials would have been drastically reduced. In fact, several follow-up studies by the National Wilms’ Tumor Study Group adopted the nested case-control design (Green et al., 2001; Warwick et al., 2010).

We defined two strata according to unfavorable versus favorable local histological assessment. We considered two scenarios with different values of n₂. In the first scenario, we set n₂ = 400 and considered five sampling strategies: case-cohort sampling; stratified case-cohort sampling; general failure-time outcome-dependent sampling; Y-dependent sampling; and optimal sampling. To ensure model identifiability and numerical stability, we required the second-phase sample size for each stratum to be greater than 60 under the optimal design. Because var(X | Z) is larger among patients with unfavorable local histological assessment than those with favorable local histological assessment, with values of 0.152 versus 0.034, we ended up selecting 156 cases and 184 controls with unfavorable local histological assessment and 30 cases and 30 controls with favorable local histological assessment. In the second scenario, we set n₂ = 1142 and compared the optimal design with case-cohort sampling, stratified case-cohort sampling, nested case-control sampling, counter-matching, and Y-dependent sampling. These designs selected all 571 cases in the second phase. The optimal design selected all patients, 156 cases and 250 controls, with unfavorable local histological assessment and 368 cases and 368 controls with favorable local histological assessment.

Table 5 shows the estimation results for the proportional hazards model under the two-phase designs and the full-cohort analysis. The log hazard-ratio estimates under most two-phase designs are close to their full-cohort counterparts. The effect of local histological assessment is not significant after adjusting for central histological assessment. The standard error estimate of central histological assessment under the optimal design is smaller than that under the other two-phase designs. These results are consistent with our theoretical and simulation results.

Table 5.

Estimates of Log Hazard Ratios, With Standard Error Estimates in Parentheses, from the Proportional Hazards Regression Analysis of the National Wilms’ Tumor Study

		Histological assessment		Tumor stage
n2	Design	Central	Local	II	III	IV	Age
400	CC	1.573 (0.359)	0.114 (0.291)	0.682 (0.125)	0.793 (0.125)	1.067 (0.141)	0.078 (0.015)
	SCC	1.579 (0.322)	0.068 (0.297)	0.677 (0.127)	0.790 (0.127)	1.092 (0.143)	0.078 (0.015)
	ODS	1.882 (0.382)	−0.127 (0.302)	0.692 (0.127)	0.795 (0.128)	1.083 (0.145)	0.080 (0.015)
	YDS	2.210 (0.269)	−0.034 (0.229)	0.704 (0.129)	0.835 (0.130)	1.113 (0.147)	0.080 (0.015)
	OPT	1.549 (0.260)	0161 (0.258)	0.666 (0.124)	0.781 (0.123)	1.151 (0.139)	0.077 (0.015)
1142	CC	1.513 (0.219)	0.128 (0.199)	0.676 (0.131)	0.789 (0.131)	1.062 (0.146)	0.077 (0.015)
	SCC	1.578 (0.193)	0.083 (0.195)	0.665 (0.113)	0.788 (0.112)	1.134 (0.132)	0.077 (0.015)
	NCC	1.510 (0.226)	0.133 (0.198)	0.675 (0.132)	0.789 (0.132)	1.063 (0.147)	0.077 (0.015)
	CM	1.585 (0.192)	0.077 (0.200)	0.666 (0.117)	0.789 (0.117)	1.134 (0.159)	0.077 (0.016)
	YDS	1.947 (0.202)	−0.109 (0.184)	0.699 (0.124)	0.838 (0.124)	1.110 (0.140)	0.072 (0.015)
	OPT	1.424 (0.185)	0.228 (0.181)	0.667 (0.111)	0.777 (0.111)	1.135 (0.141)	0.075 (0.015)
4028	FC	1.444 (0.135)	0.203 (0.144)	0.662 (0.122)	0.802 (0.121)	1.137 (0.135)	0.071 (0.015)

NOTE: CC, SCC, ODS, YDS, OPT, NCC, CM, and FC denote case-cohort sampling, stratified case-cohort sampling, general failure-time outcome-dependent sampling, Y-dependent sampling, optimal design, nested case-control sampling, counter-matching, and full-cohort, respectively. Estimates of log hazard ratios and standard errors under the CC, SCC, ODS, NCC, and CM designs are averaged over 1000 replicates.

5. DISCUSSION

As mentioned in Section 1, the existing literature on two-phase studies is concerned primarily with the inference procedures rather than the design aspects. In particular, Tao et al. (2017) studied efficient inference under two-phase sampling but did not consider design efficiency at all. To investigate design efficiency, one has to know exactly how the design parameter affects the efficiency bound. To this end, Theorem 1 provides for the first time an explicit form for the efficiency bound. It reveals an important fact that the efficiency depends on the conditional variance of the expensive covariate given inexpensive covariates. Theorem 2, together with Corollaries 1 and 2, provides the optimal sampling rules for two-phase studies. No such result exists in the literature, despite extensive prior research on two-phase studies. Indeed, our work shows that the commonly used two-phase designs are not optimal. The proofs of Theorems 1 and 2 and Corollaries 1 and 2 require considerable technical innovation.

As shown in Section 2.4, the optimal design for linear regression does not need to stratify on Z. The optimal designs for logistic regression and proportional hazards regression do not need to stratify on Z when γ = 0 and var(X | Z) is a constant. In other situations, we need to divide Z into a few strata when implementing the “optimal” design. Discretizing Z is a common practice to facilitate implementation of two-phase studies. The resulting design should converge to the optimal one as the number of strata increases.

The efficiency bound under the condition of β = o(1) is of practical importance because design efficiency matters the most when β is small, and it provides a good approximation to the efficiency bound for large β, as confirmed by our numerical studies. In the simulation studies, we considered β as large as 0.5, which corresponds to 50% of the error variance, odds ratio of 1.65, and hazard ratio of 1.65 under the linear, logistic, and proportional hazards models, respectively. For the National Heart, Lung, and Blood Institute Exome Sequencing Project, the estimates of the genetic effects on standardized log-transformed body mass index range from −0.39 to 0.32. For genetic studies with binary traits, the odds ratio estimates are rarely larger than 1.3 (Schizophrenia Working Group of the Psychiatric Genomics Consortium, 2014; Xue et al., 2018). Thus, the values of β is our simulation studies cover the typical values in genetic studies, for which two-phase designs are most commonly adopted. For the National Wilms’ Tumor Study, the hazard ratio for central histology is 4.24. In all these situations, the proposed designs are more efficient than the existing designs.

Our theory does not require every study subject to have a positive probability of being selected in the second phase and thus can accommodate the outcome-dependent sampling and residual-dependent sampling described in Lin et al. (2013), the Y-dependent sampling proposed by Lawless (2018), and the optimal design. Naturally, we can estimate only the parameters that are informed by the observed data. For example, if we sample only from the extreme tails of the outcome distribution, then we cannot nonparametrically identify the distribution in the middle, although we can estimate the regression parameters. The existing semiparametric efficiency theory with missing data (Robins et al., 1995) requires positive selection probability for every study subject, so as to identify all parameters.

We evaluated the efficiencies of existing two-phase designs and developed optimal designs. A closely-related problem is to calculate the power and sample size for a specific design. The variance formula given in (2) can be used for power and sample size calculations under any two-phase design, provided that the first-phase data and the first and second moments of the conditional distribution of X given Z are available.

We focused on the main effect of X. If the primary interest lies instead in the interactions between X and Z, then we can include those interactions in the linear predictor μ(X,Z) and derive the corresponding optimal designs. In this case, the design efficiency for logistic regression may depend on stratum sizes even when var(X | Z) is a constant.

We assumed that X is a scalar. For multivariate X, var(D_μ | R = 1,Z) is still a scalar, whereas var(X | Z) becomes a matrix. We can still use Theorem 1 to calculate V_β for any two-phase design. The added complexity lies in the estimation of var(X | Z). We can define the design efficiency based on the trace or determinant of V_β, with the corresponding optimal designs being “A-optimal” or “D-optimal”, respectively. Optimality criteria have been discussed in the design of experiments literature; see Fedorov and Leonov (2013). The use of different optimality criteria, such as the determinant, trace, or eigenvalues of the covariance matrix, can yield different optimal designs, and which should be chosen in practice depends on the scientific question of interest. Because var(D_μ | R = 1,Z) is a scalar, the optimal designs still select subjects with the largest or smallest values of D_μ in each stratum of Z and favors the strata with the largest values of the trace or determinant of var(X | Z). Theorem 2 and Corollaries 1 and 2 with multivariate X can be derived similarly to the case of a scalar X.

Some of the early research on two-phase designs was concerned with the main effects of Z, with X as an expensive confounder, and the inference procedures were typically based only on the second-phase data (White, 1982; Breslow and Cain, 1988). Because our efficient inference procedures utilize the data on Z for all study subjects, our estimator of γ under any two-phase design is essentially as efficient as the maximum likelihood estimator based on the full data.

We dealt with a single outcome. In large-scale cohort studies and electronic heath record systems, a number of potentially correlated outcomes are observed. An interesting topic of investigation is the optimal two-phase design when multiple continuous outcomes are of equal importance. Tao et al. (2015) considered two multivariate outcome-dependent sampling designs: the first design selects an equal number of subjects from the upper and lower tails of each outcome distribution; the second design selects subjects from one tail of each outcome distribution and uses a random sample as a common comparison group. Although their simulation results indicated that the first design is more efficient than the second one, it is unclear whether or not this conclusion holds broadly. Another interesting topic is the optimal design when the outcome is longitudinal repeated measures (Schildcrout et al., 2013). Our framework can be used to derive optimal designs for studies with multiple or longitudinal outcomes.

APPENDIX: Technical Details

Let S_η(h₁) denote the score for η along the submodel ϵ → η_ϵ(h₁) for one complete Let observation (Y, X, Z), where h₁ is the tangent direction along this submodel in that dη_ϵ(h₁) / dϵ_|ϵ=0 = h₁, and η₀(h₁) = η. Let U_θ denote the score for θ,U_η(h₁) denote the score for η along the submodel η_ϵ(h₁), and U_f (h₂) denote the score for f along the submodel {1 + ϵh₂(x, z)}f(x, z) under the two-phase design, where h₂ belongs to $L_2^0(f)=\left\{h:\int h\mathit{\text{\hspace{0.17em}fdxdz}}=0,\int h^2\mathit{\text{\hspace{0.17em}fdxdz}}<\infty \right\}$. Clearly,

$$\begin{gathered} U_{\mathit{\theta }}=R{D}_{\mu }{\left(1,X,{\mathit{Z}}^{\text{T}}\right)}^{\text{T}}+(1-R)\text{E}\left\{D_{\mu }{\left(1,X,{\mathit{Z}}^{\text{T}}\right)}^{\text{T}}|Y,\mathit{Z}\right\}, \\ {U}_{\eta }\left(h_1\right)=R{S}_{\eta }\left(h_1\right)+(1-R)\text{E}\left\{S_{\eta }\left(h_1\right)|Y,\mathit{Z}\right\}, \\ {U}_f\left(h_2\right)=R{h}_2(X,\mathit{Z})+(1-R)\text{E}\left\{h_2(X,\mathit{Z})|Y,\mathit{Z}\right\}. \end{gathered}$$

The information operator is

$$\left(\begin{array}{ccc}{U}_{\mathit{\theta }}^{*}{U}_{\mathit{\theta }}& U_{\mathit{\theta }}^{*}{U}_{\eta }& U_{\mathit{\theta }}^{*}{U}_f\\ U_{\eta }^{*}{U}_{\mathit{\theta }}& U_{\eta }^{*}{U}_{\eta }& U_{\eta }^{*}{U}_f\\ U_f^{*}{U}_{\mathit{\theta }}& U_f^{*}{U}_{\eta }& U_f^{*}{U}_f\end{array}\right),$$

where $U_{\mathit{\theta }}^{*}$, $U_{\eta }^{*}$ and $U_f^{*}$ are the adjoint operators of U_θ, U_η, and U_f, respectively. where β = 0, D_μ and S_η(h₁) do not depend on X, and the calculations of the information operators can be simplified greatly. We utilize this property to derive the semiparametric efficiency bound of estimating β under general two-phase designs.

Let θ₀, η₀, and f₀ be the true values of θ, η, and f, respectively. We impose the following regularity conditions:

• Condition A.1. The set of covariates (X, Z) has bounded support.

• Condition A.2. If there exist two sets of parameters (θ₁, η₁, f₁) and (θ₂, η₂, f₂) such that

  $$p_{{\mathit{\theta }}_1,n_2}(Y|X,\mathit{Z})f_1(X,\mathit{Z})=p_{{\mathit{\theta }}_2,n_2}(Y|X,\mathit{Z})f_2(X,\mathit{Z}),$$

  where (Y, X, Z) lies in $\mathcal{C}=\{(y,x,\mathit{z}):\text{Pr}(R=1|y,\mathit{z})>0\}$, then θ₁ = θ₂, η₁ = η₂, and f₁ = f₂. In addition, if there exists a constant vector v such that

  $${\left[\partial \text{log}\left\{p_{{\mathit{\theta }}_0,{\eta }_0}\left(y_1|x,\mathit{z}\right)/p_{{\mathit{\theta }}_0,{\eta }_0}\left(y_2|x,\mathit{z}\right)\right\}/\partial \mathit{\theta }\right]}^{\text{T}}v=0$$

  for any $\left(y_i,x,\mathit{z}\right)\in \mathcal{C}(i=1,2)$, then ν = 0.

• Condition A.3. The density function f₀ is positive in its support and q-times continuously differentiable with respect to a suitable measure, where q > d_z / 2, and d_z is the dimension of Z.

• Condition A.4. The function E(R | Y, Z) is q-times continuously differentiable with respect to Z in its support.

Remark A.1. Conditions A.1–A.4 correspond to Conditions (C.1)–(C.4) in Tao et al. (2017); see Remark S.1 in Tao et al. (2017) for discussion of these conditions.

Because α, β, and γ can be perturbed independently, we can write $U_{\mathit{\theta }}^{*}{U}_{\mathit{\theta }}$ as

$$\left(\begin{array}{ccc}{U}_{\alpha }^{*}{U}_{\alpha }& U_{\alpha }^{*}{U}_{\beta }& U_{\alpha }^{*}{U}_{\gamma }\\ U_{\beta }^{*}{U}_{\alpha }& U_{\beta }^{*}{U}_{\beta }& U_{\beta }^{*}{U}_{\gamma }\\ U_{\gamma }^{*}{U}_{\alpha }& U_{\gamma }^{*}{U}_{\beta }& U_{\gamma }^{*}{U}_{\gamma }\end{array}\right),$$

where U_α, U_β and U_γ denote the scores for α, β, and γ, respectively, and $U_{\alpha }^{*}$, $U_{\beta }^{*}$ and $U_{\gamma }^{*}$ denote the adjoint operators of U_α, U_β and U_γ, respectively. We state and prove the following two lemmas, which will be used in the proof of Theorem 1.

Lemma A.1. When β = 0, the information operators for (θ, η, f) are

$$U_{\alpha }^{*}{U}_{\alpha }=\text{E}\left(D_{\mu }^2\right),U_{\gamma }^{*}{U}_{\gamma }=\text{E}\left(D_{\mu }^2\mathit{Z}{\mathit{Z}}^{\text{T}}\right),U_{\alpha }^{*}{U}_{\gamma }=\text{E}\left(D_{\mu }^2{\mathit{Z}}^{\text{T}}\right),$$

$$U_{\alpha }^{*}{U}_{\beta }=\text{E}\left\{D_{\mu }^2\text{E}(X|\mathit{Z})\right\},U_{\beta }^{*}{U}_{\gamma }=\text{E}\left\{D_{\mu }^2\text{E}(X|\mathit{Z}){\mathit{Z}}^{\text{T}}\right\},$$

$$U_{\beta }^{*}{U}_{\beta }=\text{E}\left\{D_{\mu }^2\text{E}{(X|\mathit{Z})}^2\right\}+\text{E}\left\{R{D}_{\mu }^2\text{\hspace{0.17em}var}(X|\mathit{Z})\right\},$$

$$U_{\alpha }^{*}{U}_{\eta }\left(h_1\right)=\text{E}\left\{D_{\mu }{S}_{\eta }\left(h_1\right)\right\},U_{\gamma }^{*}{U}_{\eta }\left(h_1\right)=\text{E}\left\{D_{\mu }\mathit{Z}{S}_{\eta }\left(h_1\right)\right\},$$

$$U_{\beta }^{*}{U}_{\eta }\left(h_1\right)=\text{E}\left\{D_{\mu }\text{E}(X|\mathit{Z})S_{\eta }\left(h_1\right)\right\},U_{\eta }^{*}{U}_{\eta }\left(h_1\right)=S_{\eta }^{*}{S}_{\eta }\left(h_1\right),$$

$$U_{\alpha }^{*}{U}_f\left(h_2\right)=0,U_{\gamma }^{*}{U}_f\left(h_2\right)=0,U_{\eta }^{*}{U}_f\left(h_2\right)=0,$$

$$U_{\beta }^{*}{U}_f\left(h_2\right)=\text{E}\left[\text{E}\left\{R{D}_{\mu }|\mathit{Z}\right\}\{X-\text{E}(X|\mathit{Z})\}{h}_2(X,\mathit{Z})\right],$$

$$U_f^{*}{U}_f\left(h_2\right)=\text{E}(R|\mathit{Z})h_2(X,\mathit{Z})+\text{E}(1-R|\mathit{Z})\text{E}\left\{h_2(X,\mathit{Z})|\mathit{Z}\right\},$$

where $S_{\eta }^{*}$ is the adjoint operator of S_η.

Proof of Lemma A.1. The calculations of the information operators follow from the derivations in the proof of Theorem S.2 in Tao et al. (2017) and the fact that Y and R are independent of X conditional on Z when β = 0. ■

Lemma A.2. Let $M_2=U_f{\left(U_f^{*}{U}_f\right)}^{-1}{U}_f^{*}$ be the projection operator onto the score space of f. Suppose that h₃ belongs to $L_2^0(\mathcal{P})$, where $\mathcal{P}$ is the probability measure indexed by (θ, η, f). When β = 0 and Conditions A.1–A.4 hold,

$$M_2{h}_3=R\text{E}{(R|\mathit{Z})}^{-1}\left\{\text{E}\left(R{h}_3/X,\mathit{Z}\right)-\text{E}\left(R{h}_3|\mathit{Z}\right)\right\}+\text{E}\left(h_3|\mathit{Z}\right),$$ (A.1)

where we define E(R | Z)⁻¹ = 0 whenever E(R | Z) = 0.

Proof of Lemma A.2. We first derive $U_f^{*}\left(h_3\right)$. By the definition of adjoint operators,

$$\langle U_f\left(h_2\right),h_3\rangle =\langle h_2,U_f^{*}\left(h_3\right)\rangle ,$$ (A.2)

where 〈·,·〉 denotes the inner product in Hilbert space. Under β = 0, Y and R are independent of X given Z, such that the left side of equation (A.2) equals

$$\begin{gathered} \text{E}\left(\left[R{h}_2(X,\mathit{Z})+(1-R)\text{E}\left\{h_2(X,\mathit{Z})|\mathit{Z}\right\}\right]h_3(Y,X,\mathit{Z})\right) \\ =\text{E}\left[\text{E}\left\{R{h}_3(Y,X,\mathit{Z})|X,\mathit{Z}\right\}{h}_2(X,\mathit{Z})\right]+\text{E}\left(\text{E}\left[\text{E}\left\{(1-R)h_3(Y,X,\mathit{Z})|\mathit{Z}\right\}{h}_2(X,\mathit{Z})|\mathit{Z}\right]\right) \\ =\text{E}\left(\left[\text{E}\left\{R{h}_3(Y,X,\mathit{Z})|X,\mathit{Z}\right\}+\text{E}\left\{(1-R)h_3(Y,X,\mathit{Z})|\mathit{Z}\right\}\right]h_2(X,\mathit{Z})\right). \end{gathered}$$

Thus,

$$U_f^{*}\left(h_3\right)=\text{E}\left\{R{h}_3(Y,X,\mathit{Z})|X,\mathit{Z}\right\}+\text{E}\left\{(1-R)h_3(Y,X,\mathit{Z})|\mathit{Z}\right\}.$$ (A.3)

Next, we calculate ${\left(U_f^{*}{U}_f\right)}^{-1}\left(h_2\right)$. Assume, without loss of generality, that ${\left(U_f^{*}{U}_f\right)}^{-1}\left(h_2\right)=A(X,\mathit{Z})h_2(X,\mathit{Z})+B(X,\mathit{Z})\text{E}\left\{h_2(X,\mathit{Z})|\mathit{Z}\right\}$, where A(X, Z) and B(X, Z) belong to L₂(f) = {h: ∫ h² fdxdz < ∞}. Clearly,

$$\begin{gathered} h_2(X,\mathit{Z})={\left(U_f^{*}{U}_f\right)}^{-1}\left(U_f^{*}{U}_f\right)\left(h_2\right) \\ =A(X,\mathit{Z})\left[\text{E}(R|\mathit{Z})h_2(X,\mathit{Z})+\{1-\text{E}(R|\mathit{Z})\}\text{E}\left\{h_2(X,\mathit{Z})|\mathit{Z}\right\}\right]+B(X,\mathit{Z})\text{E}\left[\text{E}(R|\mathit{Z})h_2(X,\mathit{Z})+\{1-\text{E}(R|\mathit{Z})\}\text{E}\left\{h_2(X,\mathit{Z})|\mathit{Z}\right\}|\mathit{Z}\right] \\ =A(X,\mathit{Z})\text{E}(R|\mathit{Z})h_2(X,\mathit{Z})+\{A(X,\mathit{Z})-A(X,\mathit{Z})\text{E}(R|\mathit{Z})+B(X,\mathit{Z})\}\text{E}\left\{h_2(X,\mathit{Z})|\mathit{Z}\right\}. \end{gathered}$$ (A.4)

Because equation (A.4) holds for all $h_2\in L_2^0(f)$, we have A(X, Z) = E(R | Z)⁻¹ and B(X, Z) = 1 – E(R | Z)⁻¹. Thus,

$${\left(U_f^{*}{U}_f\right)}^{-1}\left(h_2\right)=\text{E}(R){(\mathit{Z})}^{-1}{h}_2(X,\mathit{Z})+\left\{1-\text{E}{(R|\mathit{Z})}^{-1}\right\}\text{E}\left\{h_2(X,\mathit{Z})|\mathit{Z}\right\}.$$ (A.5)

By combining equations (A.3) and (A.5), we obtain

$$\begin{gathered} {\left(U_f^{*}{U}_f\right)}^{-1}{U}_f^{*}\left(h_3\right)=\text{E}{(R|\mathit{Z})}^{-1}\left[\text{E}\left(R{h}_3|X,\mathit{Z}\right)+\text{E}\left\{(1-R)h_3|\mathit{Z}\right\}\right] \\ +\left\{1-\text{E}{(R|\mathit{Z})}^{-1}\right\}\text{E}\left[\text{E}\left(R{h}_3|X,\mathit{Z}\right)+\text{E}\left\{(1-R)h_3|\mathit{Z}\right\}|\mathit{Z}\right] \\ =\text{E}{(R|\mathit{Z})}^{-1}\left\{\text{E}\left(R{h}_3|X,\mathit{Z}\right)-\text{E}\left(R{h}_3|\mathit{Z}\right)\right\}+\text{E}\left(h_3|\mathit{Z}\right), \\ {M}_2{h}_3=U_f{\left(U_f^{*}{U}_f\right)}^{-1}{U}_f^{*}\left(h_3\right)=R\text{E}{(R|\mathit{Z})}^{-1}\left\{\text{E}\left(R{h}_3|X,\mathit{Z}\right)-\text{E}\left(R{h}_3|\mathit{Z}\right)\right\}+\text{E}\left(h_3|\mathit{Z}\right). \end{gathered}$$ (A.6)

This concludes the proof of Lemma A.2. ■

Proof of Theorem 1. By Lemma A.1, $U_{\alpha }^{*}{U}_f\left(h_2\right)=0,U_7^{*}{U}_f\left(h_2\right)=0$, and $U_{\eta }^{*}{U}_f\left(h_2\right)=0$, i.e., the score space for (α, γ, η) and f are orthogonal when β = 0. Thus, the inverse of the efficiency bound for estimating β with one observation is

$$\begin{gathered} {\Sigma }_0=U_{\beta }^{*}{U}_{\beta }-\langle M_1{U}_{\beta },U_{\beta }\rangle -\langle M_2{U}_{\beta },U_{\beta }\rangle \\ =\text{E}\left\{D_{\mu }^2\text{E}{(X|\mathit{Z})}^2\right\}-\langle M_1{U}_{\beta },U_{\beta }\rangle -\langle M_2{U}_{\beta },U_{\beta }\rangle +\text{E}\left\{R{D}_{\mu }^2\text{\hspace{0.17em}var}(X|\mathit{Z})\right\}, \end{gathered}$$ (A.7)

where M₁ is the projection operator onto the score space of (α, γ, η). Clearly,

$$M_1=\left[\begin{array}{lll}{U}_{\alpha }\hfill & U_{\gamma }\hfill & U_{\eta }\hfill \end{array}\right]{\left[\begin{array}{ccc}{U}_{\alpha }^{*}{U}_{\alpha }& U_{\alpha }^{*}{U}_{\gamma }& U_{\alpha }^{*}{U}_{\eta }\\ U_{\gamma }^{*}{U}_{\alpha }& U_{\gamma }^{*}{U}_{\gamma }& U_{\gamma }^{*}{U}_{\eta }\\ U_{\eta }^{*}{U}_{\alpha }& U_{\eta }^{*}{U}_{\gamma }& U_{\eta }^{*}{U}_{\eta }\end{array}\right]}^{-1}\left[\begin{array}{c}{U}_{\alpha }^{*}\\ U_{\gamma }^{*}\\ U_{\eta }^{*}\end{array}\right],$$ (A.8)

$${\Sigma }_1=\text{E}\left\{D_{\mu }^2\text{E}{(X|\mathit{Z})}^2\right\}-\langle M_1{U}_{\beta },U_{\beta }\rangle .$$

We wish to calculate 〈M₂U_β,U_β〉. By setting h₃ = U_β in Lemma A.2, we have

$$M_2{U}_{\beta }=R\text{E}{(R|\mathit{Z})}^{-1}\left\{E\left(R{U}_{\beta }|X,\mathit{Z}\right)-E\left(R{U}_{\beta }|\mathit{Z}\right)\right\}+E\left(U_{\beta }|\mathit{Z}\right).$$ (A.9)

We evaluate the expressions E(RU_β|X, Z), E(RU_β|Z), and E(U_β| Z) on the right side of equation (A.9) as follows:

$$\begin{gathered} \text{E}\left(R{U}_{\beta }|X,\mathit{Z}\right)=\text{E}\left[R\left\{R{D}_{\mu }X+(1-R)\text{E}\left(D_{\mu }X|Y,\mathit{Z}\right)\right\}|X,\mathit{Z}\right] \\ =\text{E}\left(R{D}_{\mu }|\mathit{Z}\right)X, \end{gathered}$$ (A.10)

$$\text{E}\left(R{U}_{\beta }|\mathit{Z}\right)=\text{E}\left\{\text{E}\left(R{U}_{\beta }|X,\mathit{Z}\right)|\mathit{Z}\right\}=\text{E}\left(R{D}_{\mu }|\mathit{Z}\right)\text{E}(X|\mathit{Z}),$$ (A.11)

$$\begin{gathered} \text{E}\left(U_{\beta }|\mathit{Z}\right)=\text{E}\left\{R{D}_{\mu }X+(1-R)\text{E}\left(D_{\mu }X|Y,\mathit{Z}\right)|\mathit{Z}\right\} \\ =\text{E}\left\{R{D}_{\mu }X+(1-R)D_{\mu }\text{E}(X|\mathit{Z})|\mathit{Z}\right\} \\ =\text{E}\left\{R{D}_{\mu }+(1-R)D_{\mu }|\mathit{Z}\right\}\text{E}(X|\mathit{Z}) \\ =0. \end{gathered}$$ (A.12)

By combining equations (A.9), (A.10), (A.11), and (A.12), we have

$$M_2{U}_{\beta }=R\text{E}{(R|\mathit{Z})}^{-1}\text{E}\left(R{D}_{\mu }|\mathit{Z}\right)\{X-\text{E}(X|\mathit{Z})\}.$$ (A.13)

In light of equation (A.13),

$$\begin{gathered} \langle M_2{U}_{\beta },U_{\beta }\rangle =\text{E}\left[R\text{E}{(R|\mathit{Z})}^{-1}\text{E}\left(R{D}_{\mu }|\mathit{Z}\right)\{X-\text{E}(X|\mathit{Z})\}\left\{R{D}_{\mu }X+(1-R)D_{\mu }\text{E}(X|\mathit{Z})\right\}\right] \\ =\text{E}\left[R\text{E}{(R|\mathit{Z})}^{-1}\text{E}\left(R{D}_{\mu }|\mathit{Z}\right)\{X-\text{E}(X|\mathit{Z})\}R{D}_{\mu }X\right] \\ =\text{E}\left[\text{E}{(R|\mathit{Z})}^{-1}\text{E}\left(R{D}_{\mu }|\mathit{Z}\right)\text{E}\left\{X^2-\text{E}(X|\mathit{Z})X|Y,\mathit{Z}\right\}R{D}_{\mu }\right] \\ =\text{E}\left[\text{E}{(R|\mathit{Z})}^{-1}\text{E}{\left(R{D}_{\mu }|\mathit{Z}\right)}^2\text{\hspace{0.17em}var}(X|\mathit{Z})\right]. \end{gathered}$$ (A.14)

By combining equations (A.7), (A.8), and (A.14), we obtain

$$\begin{gathered} {\sum }_0={\sum }_1+\text{E}\left[\left\{\text{E}\left(R{D}_{\mu }^2|\mathit{Z}\right)-\text{E}{(R|\mathit{Z})}^{-1}\text{E}{\left(R{D}_{\mu }|\mathit{Z}\right)}^2\right\}\text{\hspace{0.17em}var}(X|\mathit{Z})\right] \\ ={\sum }_1+\text{E}\left[R\text{\hspace{0.17em}var}\left\{D_{\mu }|R=1,\mathit{Z}\right\}\text{\hspace{0.17em}var}(X|\mathit{Z})\right]. \end{gathered}$$ (A.15)

Because Σ₀ is a continuous function of β, equation (A.15) continues to hold when β = o(1). Taking the inverse of both sides of equation (A.15) yields equation (2). ■

Proof of Theorem 2. By Theorem 1, for any fixed E(R | Z) = g > 0, we wish to find Pr(R = 1| D_μ, Z) that maximizes var(D_μ | R = 1, Z), which is equal to $\text{E}\left(R{D}_{\mu }^2|\mathit{Z}\right)/\text{E}(R|\mathit{Z})-\text{E}{\left(R{D}_{\mu }|\mathit{Z}\right)}^2/\text{E}{(R|\mathit{Z})}^2$. If we further fix E(RD_μ | Z) = m, then this maximization is equivalent to maximizing $\text{E}\left(R{D}_{\mu }^2|\mathit{Z}\right)$ subject to the constraints of E(R | Z) = g and E(RD_μ | Z) = m. That is, we wish to find Pr(R = 1| D_μ, Z) that maximizes

$${\int }_{d_{\mu }}{d}_{\mu }^2\text{Pr}\left(R=1|D_{\mu }=d_{\mu },\mathit{Z}\right)dF\left(d_{\mu }|\mathit{Z}\right)$$

subject to the constraints

$${\int }_{d_{\mu }}\text{Pr}\left(R=1|D_{\mu }=d_{\mu },\mathit{Z}\right)dF\left(d_{\mu }|\mathit{Z}\right)=g,$$ (A.16)

$${\int }_{d_{\mu }}{d}_{\mu }\text{Pr}\left(R=1|D_{\mu }=d_{\mu },\mathit{Z}\right)dF\left(d_{\mu }|\mathit{Z}\right)=m.$$ (A.17)

Using the method of Lagrange multipliers, we aim to maximize

$${\int }_{d_{\mu }}\left(d_{\mu }^2-{\xi }_1-{\xi }_2{d}_{\mu }\right)\text{Pr}\left(R=1|D_{\mu }=d_{\mu },\mathit{Z}\right)dF\left(d_{\mu }|\mathit{Z}\right),$$

where ξ₁ and ξ₂ are the Lagrange multipliers. By the arguments in the proof of the Neyman–Pearson lemma (Lehmann and Romano, 2005), we can show that

$$\text{Pr}\left(R^{\text{opt}}=1|D_{\mu }=d_{\mu },\mathit{Z}\right)=\{\begin{array}{ll}1\hfill & \text{if }\left(d_{\mu }^2-{\xi }_1-{\xi }_2{d}_{\mu }\right)>0,\hfill \\ c_{\mathit{Z}}\hfill & \text{if }\left(d_{\mu }^2-{\xi }_1-{\xi }_2{d}_{\mu }\right)=0,\hfill \\ 0\hfill & \text{otherwise,}\hfill \end{array}$$

where c_Z is a constant such that pr(R^opt = 1|D_μ = d_μ, Z) satisfies constraints (A.16) and (A.17). This immediately leads to expression (5). ■

Proof of Corollary 1. Again, we appeal to the arguments in the proof of the Neyman–Pearson lemma (Lehmann and Romano, 2005). Specifically, if R′ is another second-phase sampling rule that satisfies budget constraint (4), then

$$\text{E}\left(\left(R_{\text{linex }}^{\text{opt }}-R^{\prime }\right)\left[{\left\{Y-\mu (\mathit{Z})\right\}}^2\text{\hspace{0.17em}var}(X|\mathit{Z})-c_0^2\right]\right)\ge 0$$

by the definition of $R_{\text{linear }}^{\text{opt }}$. This inequality can be rewritten as

$$\begin{gathered} \text{E}\left[R_{\text{linex }}^{\text{opt }}{\left\{Y-\mu (\mathit{Z})\right\}}^2\text{\hspace{0.17em}var}(X|\mathit{Z})\right]-\text{E}\left[R^{\prime }{\left\{Y-\mu (\mathit{Z})\right\}}^2\text{\hspace{0.17em}var}(X|\mathit{Z})\right] \\ \ge c_0^2\text{E}\left(R_{\text{linear }}^{\text{opt }}-R^{\prime }\right)=0. \end{gathered}$$

It follows that

$$\begin{gathered} \text{E}\left[R_{\text{linear }}^{\text{opt }}{\left\{Y-\mu (\mathit{Z})\right\}}^2\text{\hspace{0.17em}var}(X|\mathit{Z})\right] \\ \ge \text{E}\left[R^{\prime }{\left\{Y-\mu (\mathit{Z})\right\}}^2\text{\hspace{0.17em}var}(X|\mathit{Z})\right]=\text{E}\left(\text{E}\left[R^{\prime }{\left\{Y-\mu (\mathit{Z})\right\}}^2|\mathit{Z}\right]\text{\hspace{0.17em}var}(X|\mathit{Z})\right) \\ \ge \text{E}\left\{R^{\prime }\text{\hspace{0.17em}var}(Y|R^{\prime }=1,\mathit{Z})\text{\hspace{0.17em}var}(X|\mathit{Z})\right\}. \end{gathered}$$ (A.18)

When β = 0, Y is independent of X given Z, and the conditional distribution of Y – μ(Z) given Z is symmetric about 0. Thus,

$$\text{E}\left[R_{\text{linear }}^{\text{opt }}\left\{Y-\mu (\mathit{Z})\right\}|\mathit{Z}\right]=0.$$ (A.19)

By combining inequality (A.18) and equality (A.19), we obtain

$$\begin{gathered} \text{E}\left\{R_{\text{linear}}^{\text{opt}}\text{\hspace{0.17em}var}(Y|R=1,\mathit{Z})\text{\hspace{0.17em}var}(X|\mathit{Z})\right\}=\text{E}\left[R_{\text{linex }}^{\text{opt }}{\left\{Y-\mu (\mathit{Z})\right\}}^2\text{\hspace{0.17em}var}(X/\mathit{Z})\right] \\ \ge \text{E}\left\{R^{\prime }\text{\hspace{0.17em}var}\left(Y|R^{\prime }=1,\mathit{Z}\right)\text{\hspace{0.17em}var}(X|\mathit{Z})\right\}. \end{gathered}$$

That is, the second-phase sampling rule $R_{\text{linear }}^{\text{opt }}$ maximizes expression (3) over all rules R′ that satisfy budget constraint (4). ■

Proof of Corollary 2. To maximize expression (9), we first fix E(R | Z) ∈[0,1] and search for the value of E(R | Y = 1, Z) that maximizes

$$\text{E}(R|Y=1,\mathit{Z})\{\text{E}(R|\mathit{Z})-\text{E}(R|Y=1,\mathit{Z})\text{E}(Y|\mathit{Z})\}$$ (A.20)

subject to the constraint

$$\text{max}\left\{1-\frac{1-\text{E}(R|\mathit{Z})}{\text{E}(Y|\mathit{Z})},0\right\}\le \text{E}(R|Y=1,\mathit{Z})\le \text{min}\left\{\frac{\text{E}(R|\mathit{Z})}{\text{E}(Y|\mathit{Z})},1\right\}.$$ (A.21)

This constraint arises from the relationship

$$\text{E}(R|\mathit{Z})=\text{E}(R|Y=1,\mathit{Z})\text{E}(Y|\mathit{Z})+\text{E}(R|Y=0,\mathit{Z})\{1-\text{E}(Y|\mathit{Z})\}$$ (A.22)

and the fact that E(R | Y = 1, Z) and E(R | Y = 0, Z) are conditional probabilities. We consider two scenarios for E(R | Z).

Scenario 1: E(R | Z) ≤ 2E(Y | Z). Let

$$\text{E}(R|Y=1,\mathit{Z})=\text{E}(R|\mathit{Z})/\{2\text{E}(Y|\mathit{Z})\}.$$ (A.23)

By equation (A.22),

$$\text{E}(R|Y=0,\mathit{Z})=\text{E}(R|\mathit{Z})/[2\{1-\text{E}(Y|\mathit{Z})\}].$$ (A.24)

Clearly, both E(R | Y = 1, Z) and E(R | Y = 0, Z) lie in [0,1], and E(R | Y = 1, Z) maximizes expression (A.20). Under this sampling rule, E(RY | Z) = E{R(1–Y) | Z}, so we should select an equal number of cases and controls in this stratum.

Scenario 2: E(R | Z) > 2E(Y | Z). The upper bound for E(R | Y =1, Z) in constraint (A.21) is one. Because E(R | Z)/ {2E(Y | Z)}>1, the maximum of expression (A.20) is attained when E(R | Y = 1, Z) = 1. By equation (A.22),

$$\text{E}(R|Y=0,\mathit{Z})=\frac{\text{E}(R|\mathit{Z})-\text{E}(Y|\mathit{Z})}{1-\text{E}(Y|\mathit{Z})}.$$

Clearly, E(RY | Z) < E{R(1 – Y) | Z}, so we should select all cases and a larger number of controls in this stratum.

By taking into account both scenarios, we see that expression (9) can be written as expression (11). We then search for the optimal E(R | Z) that maximizes expression (11) subject to budget constraint (4).

Now consider the special case when var(X | Z) is a constant and E(R) ≤ 2E(Y). We first show that there exists a design such that E(R | Z) ≤ 2E(Y | Z). In fact, if we define (z₀ (= inf {(z (: 2Pr(Y = 1,(Z(>(z₀ () ≤τ}, which is finite, then the design with E(R | Z = z) = 2E(Y | Z = z) for (z (>(z₀ (and E(R| Z = z₀) = τ − Pr(R = 1, (Z (>(z₀ () satisfies the condition. For any such design, if we further let E(R | Y = 1, Z) = E(R | Z) / {2E(Y | Z)}, then the value of expression (11) equals constant var(X)τ / 4. On the other hand, expression (11) is bounded by var(X)τ / 4 because

$$\text{E}(Y|\mathit{Z})\left\{1-\frac{\text{E}(Y|\mathit{Z})}{\text{E}(R|\mathit{Z})}\right\}\le \frac{\text{E}(R|\mathit{Z})}{4}.$$

Hence, any design that satisfies E(R | Z) ≤ 2E(Y | Z) and

$$\text{E}(R|Y=1,\mathit{Z})=\text{E}(R|\mathit{Z})/\{2\text{E}(Y|\mathit{Z})\}$$

is optimal. ■