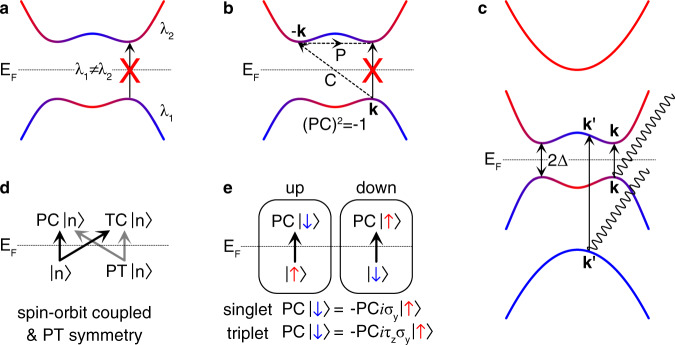
Fig. 2. Selection rules in clean superconductors.

a Selection rule by unitary symmetry. λ_1,2 are eigenvalues of a k-local unitary symmetry operator. No optical excitation occurs between two states with different eigenvalues. b Selection rule by $\mathfrak{C}$ symmetry. The case with $\mathfrak{C}=\mathrm{PC}$ is shown. No optical transition occurs between PC-related states when (PC)² = −1. c Optical excitation channels in $\mathfrak{C}$-symmetric superconductors in the clean limit. At low photon energies comparable to the superconducting gap 2Δ, the relevant excitations are spectrum-inversion-symmetric (SIS) ones, i.e., from energy −E to E. For nondegenerate bands, they are transitions between $\mathfrak{C}$-related pairs. d, e Optical excitations in spin-degenerate systems with and without spin–orbit coupling, respectively. (here, the order of d and e has been changed in order to match the label in the figure.) In d, $\mathfrak{T}=\mathrm{PT}$ symmetry with (PT)² = −1 imposes Kramers degeneracy. As a state $∣n⟩$ can be excited to one of two SIS states, $\mathrm{PC}∣n⟩$ and $\mathrm{PT}\left(\mathrm{PC}∣n⟩\right)=\mathrm{TC}∣n⟩$, the excitation from $∣n⟩$ is possible even when one transition channel, from $∣n⟩$ to $\mathrm{PC}∣n⟩$, is blocked by (PC)² = −1. The same applies to the excitation from $\mathrm{PT}∣n⟩$. In e, the boxes labeled up and down indicate the spin up and down eigenspace (s_z = ℏ/2 and − ℏ/2, respectively). Since C reverses the spin (the anti-particle of a spin-up electron carries the down spin) while P does not change the spin, PC reverses the spin. Its combination with the spin rotation around the y axis, which is iσ_y for spin-singlet pairing, acts within a s_z sector. For spin-triplet pairing, the spin rotation around the y-axis acts on the particle and hole sector with an opposite sign due to the spin carried by the Cooper pair, so the additional τ_z is introduced (see section 3 in the “Methods”). Optical excitations are forbidden when $\mathfrak{C}$ defined within a spin sector, which is −iPCσ_y for singlet pairing (−iPCτ_zσ_y for triplet pairing), satisfies ${\mathfrak{C}}^2=-1$. E_F is the Fermi level in all figures.