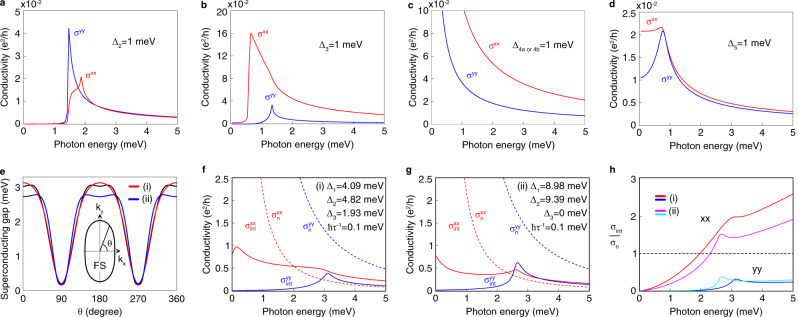
Fig. 3. Optical conductivity in a model of superconducting FeSe near Γ at zero temperature.

Model parameters in the normal state are adapted from ref. ³⁹ (see section 6 in the Methods). The xx and yy components of the conductivity tensor is shown in red and blue, respectively, in (a–d, f, g). a–d Nonzero intrinsic optical conductivity tensors for each constant pairing function. See Methods and Table 2 for the matrix form and symmetries of the six constant pairing functions Δ₁–Δ_4a, Δ_4b, and Δ₅. The case of the Δ₁ pairing is not shown as the conductivity is identically zero. e Superconducting gap similar to the experimentally observed gap. FS and the ellipse enclosing it represent the Fermi surface. Red and blue curves correspond to the choice of pairing functions (i) Δ₁ = 4.09 meV, Δ₂ = 4.82 meV, and Δ₃ = 1.93 meV or (ii) Δ₁ = 8.98 meV, Δ₂ = 9.39 meV, and Δ₃ = 0 meV, respectively. They are least-square fits with and without Δ₃ to $\mathrm{\Delta }\left(\theta \right)=\mid 2.06+1.42\cos \left(2\theta \right)-0.44\cos \left(4\theta \right)\mid$ (shown as a black curve) that was obtained in ref. ¹⁵ from experimental data. f, g Conductivity with pairing functions used in (e). σ_int is the internal optical conductivity in the superconducting state (solid lines), and σ_n is the Drude conductivity in the normal state (dashed lines). The disorder-mediated conductivity in the superconducting state is expected to be comparable to σ_n. h Ratio of σ_int and σ_n. Red and blue curves are for parameters in (f), and magenta and cyan are for parameters in (g). xx and yy indicate the component of the conductivity tensor. σ^xy and σ^yx are not shown in all plots because they vanish due to M_x symmetry.