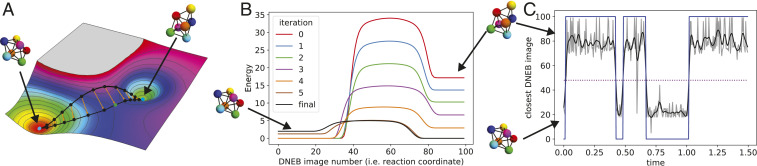
Fig. 3.

(A) Illustration of the DNEB method (39) for finding the transition state between two local energy minima, which in our case, corresponds to metastable seven-particle clusters. Given such an energy landscape, we construct a series of $n_I=100$ images that span the two minima and are connected by high-dimensional springs. Keeping the two end points fixed to the minima, the energy of the ensemble is minimized collectively. The resulting $n_I$ images give the steepest descent path from one minimum to the other, traversing the saddle point. Thus, the image with the largest energy approximates the saddle point, or transition state, and we can use the image number as a one-dimensional representation of the steepest descent path, or reaction coordinate. However, note that the spacing between images is not imposed, and so, the image number is not a direct measure of distance. SI Appendix has more details. (B) Energy (in $k_{B}T$) along the steepest descent path after successive iterations of the optimization algorithm. For clarity, the minimum energy along the path is subtracted. Note that the regions of constant energy at the beginning and end of the path correspond to global rotations of the cluster. (C) Verification of the transition rates via MD simulation. Periodic snapshots from MD simulations are mapped to the steepest descent path found through the DNEB calculation (gray). Noise is reduced using a Butterworth low-pass filter (black) and then binarized (blue). The dashed line represents the threshold for binarizing the signal and corresponds to the image with the highest energy (i.e., $R_t$). Transition rates are calculated from the dwell times of the binarized signal.