Elastic amplification of the Rayleigh–Taylor instability in solidifying melts

Significance

Patterns resulting from successive far-from-equilibrium processes are common in nature. Yet, they are challenging to investigate, model, and translate to engineering owing to their complexity coupled to fluctuating developmental conditions. Here we introduce a comparatively simpler system combining a fluidic instability and large solid deformations in solidifying melts to produce soft solids with complex surface geometry. We fully rationalize this different kind of pattern comprising elongated hair-like features using the framework of continuum mechanics. Our work is relevant to the broad range of problems where mechanical deformations and solidification are concomitant and paves the way for the use of multistep moldless approaches for the assembly of complex materials.

Abstract

The concomitant mechanical deformation and solidification of melts are relevant to a broad range of phenomena. Examples include the preparation of cotton candy, the atomization of metals, the manufacture of glass fibers, and the formation of elongated structures in volcanic eruptions known as Pele’s hair. Usually, solid-like deformations during solidification are neglected as the melt is much more malleable in its initial liquid-like form. Here we demonstrate how elastic deformations in the midst of solidification, i.e., while the melt responds as a very soft solid ($G\sim 100$ Pa), can lead to the formation of previously unknown periodic structures. Namely, we generate an array of droplets on a thin layer of liquid elastomer melt coated on the outside of a rotating cylinder through the Rayleigh–Taylor instability. Then, as the melt cures and goes through its gelation point, the rotation speed is increased and the drops stretch into hairs. The ongoing solidification eventually hardens the material, permanently “freezing” these elastic deformations into a patterned solid. Using experiments, simulation, and theory, we demonstrate that the formation of our two-step patterns can be rationalized when combining the tools from fluid mechanics, elasticity, and statistics. Our study therefore provides a framework to analyze multistep pattern formation processes and harness them to assemble complex materials.

The mechanical properties of common materials are usually time invariant, such that these quantities typically enter as constants in the continuum mechanics models classically used in hydrodynamics (1) and elasticity (2). Yet, the microstructure of a material may evolve through time due to biological, chemical, or physical processes, thereby affecting its macroscopic properties which become time dependent. For instance, thixotropic fluids (3), growing tissues (4), swelling gels (5), phase separating systems (6), shape-memory polymers (7), and solidifying melts (8) all have time-varying properties. In Nature, phase transitions coupled to mechanical processes yield a broad range of morphologies including elongated glass threads (9), icicles (10), and penitentes (11). In engineering, melts which transition from liquid to solid are widely used to “freeze” the deformations induced in the liquid state into solid materials. Examples include the glass float and rotational spinning processes (12, 13), the foaming of ceramics (14), three-dimensional printing (15, 16), and the fabrication of thin shells via coating (17), as well as the functionalization of materials using fluid instabilities (18–20).

Continuously solidifying melts explore all of the intermediate rheological states between liquid and solid, thereby providing an opportunity to combine fluid-like and elastic-like deformations in the same material to achieve unprecedented structures. Yet, mechanical instabilities and the patterns they generate are primarily studied using fixed material properties, whether in liquids (1), elastic solids (21–24), viscoelastic materials (25), or multiphase problems (26, 27). Conversely, there are examples of complex natural structures formed by successive far-from-equilibrium nonlinear processes, e.g., in biology (28, 29) and geomorphology (30). Porting multistep pattern formation to comparatively simpler model systems, e.g., melts, could unveil additional physics and open more possibilities in engineering.

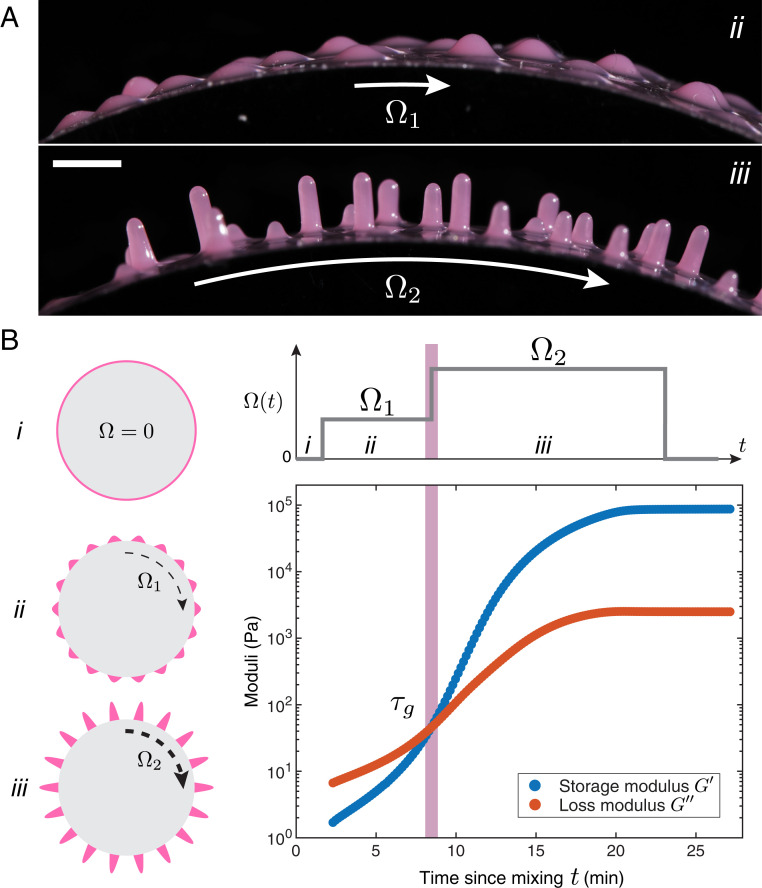
Here, we report a different kind of pattern formation involving the elastic amplification of the liquid Rayleigh–Taylor instability in curing elastomers. Our pattern comprises a regular array of hairs. We first trigger the Rayleigh–Taylor instability in a thin layer of liquid melt coated on the outside of a rotating cylinder to produce an array of seed droplets (20). In the midst of solidification, the rotation speed of the substrate is suddenly increased to elastically deform the drop pattern into hairs (Fig. 1A). As the elastomer continues to cure, the newly developed hairs are “frozen” to form a pristine elastic material that stays in place even when the rotation of the substrate ceases.

Fig. 1.

From drops to hairs. (A) Side view comparing the droplets and hairs obtained with VPS-8 at ${\mathrm{\Omega }}_1=400$ rpm, ${\mathrm{\Omega }}_2=\mathrm{1,000}$ rpm, $t^{*}=7$ min. (Scale bar, 3 mm.) (B) Schematic of the experiment coupled with the rheology data of VPS-8 curing in oscillatory shear (strain $5\%$, frequency 0.5 Hz). In step i, a cylinder is initially coated with a liquid elastomer melt undergoing curing. In step ii, while the melt remains liquid ($G^{{}^{″}}\gg G^{\prime }$) the cylinder is rotated at a speed ${\mathrm{\Omega }}_1$ to form an array of droplets through the Rayleigh–Taylor instability. In step C, when the melt becomes predominantly elastic, i.e., for $t^{*}\gtrsim {\tau }_c$ with ${\tau }_c$ the gelation point, the rotation speed is increased to ${\mathrm{\Omega }}_2$ to stretch the droplets into hairs. The rotation is finally stopped when the polymer is fully cured.

From Drops to Hairs.

Our methodology is outlined in Fig. 1B. Using elastomers that spontaneously cure when reagents are mixed (vinylpolysiloxane [VPS-8] and polydimethylsiloxane [PDMS]) (Materials and Methods), we coat the outside of a cylinder of radius $R$ with a uniform layer of the melt (step i). While the melt is still liquid, i.e., while its loss modulus $G^{{}^{″}}$ is much higher than its storage modulus $G^{\prime }$, the cylinder is rotated at a speed ${\mathrm{\Omega }}_1$ (step ii). The resulting centrifugal acceleration $R{\mathrm{\Omega }}_1^2$ triggers the liquid Rayleigh–Taylor instability and generates an array of pendant drops whose characteristic size is ${\ell }_c=\sqrt{\gamma /\left(\rho R{\mathrm{\Omega }}_1^2\right)}$, the generalized capillary length with $\gamma$ the melt interfacial tension and $\rho$ its density (20). As the polymer cures, cross-links form in the initially disconnected polymer network, thereby increasing $G^{\prime }$. After a time ${\tau }_g$, the reaction reaches the gel point (8) and the melt becomes predominantly elastic ($G^{\prime }>G^{{}^{″}}$), albeit still very soft ($G^{\prime }\left({\tau }_g\right)\sim 100$ Pa) compared to the fully cured elastomer ($G^{\prime }\left(\infty \right)>10^5$ Pa) (Fig. 1B). At a time $t^{*}\gtrsim {\tau }_g$, the cylinder rotation speed is increased to reach ${\mathrm{\Omega }}_2>{\mathrm{\Omega }}_1$, thereby stretching the array of soft drops into elongated hair-like structures (step iii). The rotation is stopped when the elastomer is fully cured.

In Fig. 1A, we show the drop pattern obtained after step ii and the hair pattern obtained after step C. The elastic deformation induced during step C does not change the wavelength of the pattern, which is set by the liquid instability. However, step C increases the amplitude of the pattern, yielding elongated structures that remain indefinitely after the rotation is halted. To rationalize the formation of these hairs, we study their growth step by step.

Seed Droplet Pattern.

The Rayleigh–Taylor instability in curing elastomer melts (20) (step ii of our experiment in Fig. 1) produces a predominantly hexagonal array of drops with a wavelength $2\pi \sqrt{2}{\ell }_c$, the linearly most unstable mode of the instability (31). The growth rate of the instability is $\tau =12\eta {\ell }_c^4/\left(\gamma {\delta }_0^3\right)\sim 1$ s with $\eta \sim 1$ Pa$\cdot$s the initial viscosity of the melt and ${\delta }_0\sim 1$ mm the initial coating thickness. This time scale is much smaller than the gelation time $\tau \ll {\tau }_g\approx 8$ min for VPS-8 (Fig. 1B). The instability thus has ample time to develop and saturate in the form of a quasistatic network of interconnected pendant drops before the gelation is point is reached (20, 32). The typical height of these drops $h_0$ is controlled by the capillary length ${\ell }_c$ as drops can grow up to $h_0\approx 2.15{\ell }_c$ before dripping. Likewise, ${\ell }_c$ dictates the spacing between drops, such that increasing the value of the initial acceleration ${\mathrm{\Omega }}_1$ ultimately results in smaller motifs (SI Appendix, section I and Fig. S2).

Elastic Deformation.

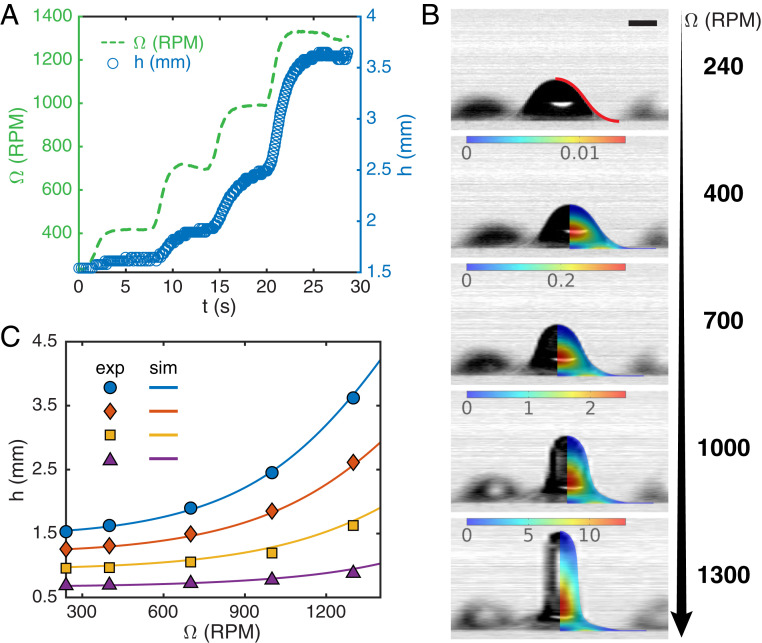
We anticipate that the shape of the hairs depends on the centrifugal acceleration, the rheology of the melt, and the initial shape of the drops. To disentangle the respective role of these contributing factors we conduct the following experiment. We increase the rotation speed of the cylinder by successive increments (Fig. 2A) and use a high-speed camera to track the deformation of individual drops during this stretching sequence (Materials and Methods and Movie S1). Using PDMS, an elastomer that cures slowly allows us to keep the material properties approximately constant during the sequence of successive acceleration (SI Appendix, Fig. S1A; ${\left.\frac{1}{G^{\prime }}\frac{\partial G^{\prime }}{\partial t}\right|}_{t\approx {\tau }_g}\approx 15$%/min).

Fig. 2.

(A) Time evolution of the height $h$ of a droplet as we increase the rotation speed $\mathrm{\Omega }$. (B) Images of the corresponding droplet after each step. The red curve shows the initial theoretical profile used in the FEM simulations whose results are superimposed on the pictures. Color bars indicate the dimensionless neo-Hookean strain energy density: $2\mathcal{W}/G$. (C) Steady-state height reached after each step for drops with different initial shapes. Solid curves show FEM simulation results for the same droplets with $G=224$ Pa. Experimental details: PDMS with curing accelerator, $R=6.36$ cm, $t^{*}=63$ min (Movie S1).

In Fig. 2A we show the height, $h\left(\mathrm{\Omega }\right)$ of an individual hair, while the corresponding shapes are shown in Fig. 2B. At each acceleration step, the drop height increases and eventually reaches a plateau a few seconds after the motor does. The higher the rotation speed, the more the hair stretches. Our methodology allows us to track 20 to 50 drops in each experiment and extract their steady-state height $h$ shown in Fig. 2C for a representative subset of drops. As evident from Fig. 2C, the final height of the hair depends on the initial drop shape, bigger drops deforming comparatively more. Additionally, the increase in height with the rotation speed appears to be nonlinear as explained next.

Right after gelation, the elastomers behave as viscoelastic solids (Fig. 1B and SI Appendix, Fig. S1A). In the following, we focus on steady-state shapes such that viscous effects can be neglected. We thus develop a purely elastic framework to rationalize the shape of the hairs. Step ii in Fig. 1B yields quasistatic drops, which are assumed to be macroscopic stress-free solids under an acceleration $R{\mathrm{\Omega }}_1^2$ after the gelation point. Using this state as our reference configuration, we model the increase in centrifugal acceleration of step C as the fictitious body force $\rho g_{\mathrm{e}\mathrm{ff}}=\rho R\left({\mathrm{\Omega }}_2^2-{\mathrm{\Omega }}_1^2\right)$. This framework was implemented in finite-element simulations (FEM) using an incompressible neo-Hookean constitutive law to represent our half-cured drops. The strain energy density is $\mathcal{W}=\left(G/2\right)\left({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2-3\right)$, with ${\lambda }_i$ the principal stretches and $G$ the shear modulus, the only material constant required in our model. The axisymmetric initial profile is obtained numerically by solving the Young–Laplace equation for pendant drops (20) (shown as the red curve in Fig. 2B) (Materials and Methods). The results of our FEM simulations are overlaid on the experimental pictures in Fig. 2B. The agreement is quantitative when using the value $G=224$ Pa for the shear modulus, in reasonable agreement with the storage modulus around gelation $G^{\prime }\left({\tau }_g\right)\sim 200$ Pa measured in the rheometer for PDMS (SI Appendix, Fig. S1A). Using this unique value of $G$, we simulate the deformations of all of the drops shown in Fig. 2C. The numerical results are shown as solid lines in Fig. 2C and quantitatively agree with the experimental data. Our simple elastic framework thus appears to be sufficient to capture the steady-state deformation of the elastomer melt right after gelation.

We now leverage our theoretical framework to get analytical insights into the physics at play. An elastic layer of uniform thickness subjected to an acceleration can destabilize into a pattern of hexagonal dimples via an elastic version of the Rayleigh–Taylor instability (23, 33). However, in our experiment the hairs develop from an array of preexisting droplets rather than a uniform layer. This difference in initial condition produces a very different final pattern. Balancing the pressure induced by the acceleration, $\rho g_{\mathrm{e}\mathrm{ff}}{h}_0$ with $h_0$ the initial drop height, and the elastic resistance of the drop, $G$, yields the nondimensional parameter

$$\alpha =\rho g_{\mathrm{e}\mathrm{ff}}{h}_0/G,$$ [1]

which is defined locally for each drop as $h_0$ varies across the sample since the drops are not perfectly monodisperse (20). A second dimensionless number, $h_0/{\ell }_c$, representing the drop shape itself is needed to fully characterize our problem.

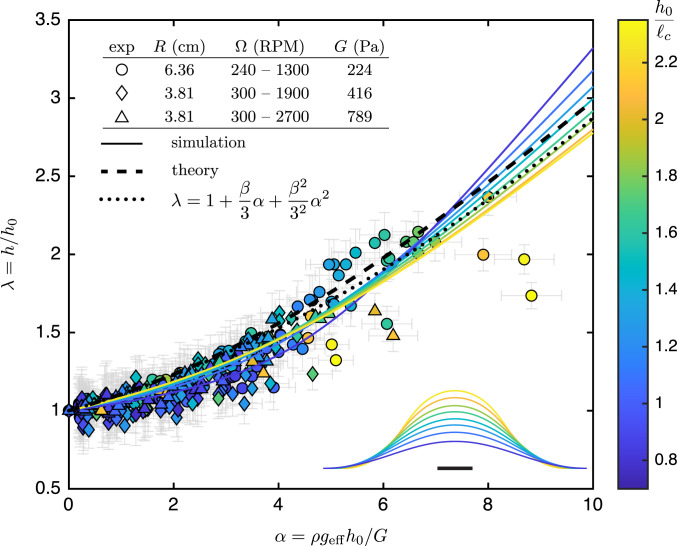
We repeat our multistep acceleration experiment to independently vary $g_{\mathrm{e}\mathrm{ff}}$ (through $R$ and $\mathrm{\Omega }$), $G$ (through $t^{*}$, the time at which the rotation speed is increased), and $h_0$. Because of the experimental uncertainties in the curing speed of the elastomer (Materials and Methods), we cannot determine $G$ precisely beforehand and rely on the FEM simulations to determine the shear modulus for each experiment. In Fig. 3 we plot the dimensionless height, or stretch, $\lambda =h/h_0$ as a function of the local rescaled acceleration $\alpha =\rho g_{\mathrm{e}\mathrm{ff}}{h}_0/G$ for all of the drops obtained across our experiments, while color coding the value of $h_0/{\ell }_c$. We find that the data collapse reasonably well, confirming the relevance of $\alpha$ in our problem. Additionally, we performed FEM simulations for the range of drop shapes shown in Fig. 3, Inset. The numerical results are shown as solid lines in Fig. 3. While these curves start to diverge past $\alpha \approx 6$, their proximity indicates the marginal influence of the details of the initial drop shape on the final deformation.

Fig. 3.

Stretch $\lambda =h/h_0$ as a function of the dimensionless gravity $\alpha =\rho g_{\mathrm{e}\mathrm{ff}}{h}_0/G$ with $g_{\mathrm{e}\mathrm{ff}}=R\left({\mathrm{\Omega }}_2^2-{\mathrm{\Omega }}_1^2\right)$ the acceleration jump. Markers represent individual PDMS droplets from three experiments whose parameters are shown in the key, and experimental uncertainties are shown as error bars. The color codes the initial droplet dimensionless height $h_0/{\ell }_c$ which defines its shape as shown in Inset. (Scale bar, ${\ell }_c$.) Colored solid curves are the results of FEM simulations, the black dashed curve is our analytical model (Eq. 3), and the dotted line is a second-order expansion of the model.

Leveraging the predominant role of $\alpha$ we derive a simplified model for $\lambda \left(\alpha \right)$ based on the minimization of the energy of the system which comprises an elastic component (the strain energy) and a potential energy (stemming from the centrifugal acceleration $g_{\mathrm{e}\mathrm{ff}}$). Assuming axisymmetry and homogeneous deformations (34, 35) (SI Appendix, section II), the total energy is

$$\mathcal{E}=\frac{G{V}_0}{2}\left({\lambda }^2+\frac{2}{\lambda }-3-2\beta \alpha \lambda \right).$$ [2]

Here, $V_0$ is the drop volume, $\lambda =h/h_0$ is the previously defined stretch, and $\beta \approx 0.29$ is a constant calculated from the initial drop shape. Minimizing the total energy with respect to the stretch ($\frac{\partial \mathcal{E}}{\partial \lambda }=0$) yields the cubic equation ${\lambda }^3-\beta \alpha {\lambda }^2-1=0$ whose real solution is

$$\begin{array}{c}\lambda \left(\alpha \right)=\frac{1}{3}\left(\beta \alpha +g\left(\alpha \right)+\frac{{\beta }^2{\alpha }^2}{g\left(\alpha \right)}\right),\\ g\left(\alpha \right)=\sqrt[3]{{\beta }^3{\alpha }^3+\left(3/2\right)\left(9+\sqrt{12{\beta }^3{\alpha }^3+81}\right)}.\end{array}$$ [3]

We plot Eq. 3 as a dashed black line and its asymptotic expansion $\lambda =1+\frac{\beta }{3}\alpha +\frac{{\beta }^2}{3^2}{\alpha }^2$ as a dotted line in Fig. 3. We find that our simplified model captures the drop elongation up to $\alpha \approx 8$. Above this value, the hairs in our experiments stretch more than expected with a wider spread of the data and are eventually torn apart for $\alpha \gtrsim 20$ (SI Appendix, Fig. S5A and Movie S2). The value $\alpha =8$ coincides with the formation of voids at the base of the hairs that break axisymmetry (SI Appendix, Fig. S5 B and C and Movie S3). These voids reveal the limitations of our theoretical framework (SI Appendix, section III); rationalizing the physics of their formation is beyond the scope of this study.

From Individual Hairs to Periodic Patterns.

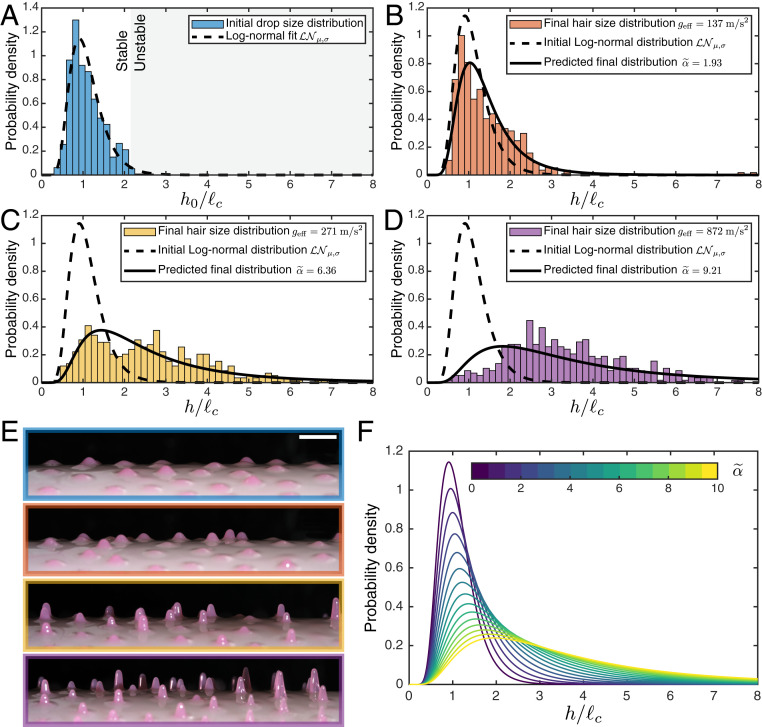
We now turn back to studying the patterns formed in our experiment. The initial liquid Rayleigh–Taylor instability (step ii in Fig. 1) produces drops whose characteristic size is ${\ell }_c$. In Fig. 4A we report the distribution of the dimensionless drop height $h_0/{\ell }_c$, normalized to represent the probability density. We observe a (positively) skewed distribution peaked around $h_0={\ell }_c$ that stops around $h_0\approx 2.2{\ell }_c$. Our initial coating in step i is thick such that dripping occurs and we can observe all possible (i.e., stable) pendant drop solutions in a single experiment (20). We find that the log-normal distribution ${\mathcal{L}\mathcal{N}}_{\mu ,\sigma }$ captures the shape of the drop distribution (dashed curve in Fig. 4A). In Fig. 4 B–D we show the final hair height distribution $h/{\ell }_c$ as we increase the effective gravity $g_{\mathrm{e}\mathrm{ff}}$. The distribution gradually widens and becomes more skewed with increasing $g_{\mathrm{e}\mathrm{ff}}$. Representative pictures of each experiment in Fig. 4E show both the increase in height and the loss of uniformity.

Fig. 4.

(A) Distribution of the initial droplet dimensionless height $h_0/{\ell }_c$ (from $n=754$ VPS-8 droplets, ${\mathrm{\Omega }}_1=400$ rpm). The dashed curve is a log-normal fit ${\mathcal{L}\mathcal{N}}_{\mu ,\sigma }$ with $\mu =0.034$ and $\sigma =0.36$. (B–D) Distribution of the final VPS-8 hair dimensionless height $h/{\ell }_c$ as the acceleration is increased from B to D, $n>379$ hairs per histogram. The initial distribution fit is shown as the dashed curve while the distribution predicted by our model is the solid curve (shear modulus fitted to $G=\left\{41.5,24.7,54.9\right\}$ Pa respectively leading to $\tilde{\alpha }=\left\{1.93,6.36,9.21\right\}$). (E) Representative pictures of the experiments shown in A–D. (Scale bar, 5 mm.) (F) Theoretical evolution of the initial drop distribution as $\tilde{\alpha }$ is increased (Eq. 4).

The hair height statistics can be understood from the deformation of individual hairs. Within an experiment, small drops experience a smaller dimensionless acceleration $\alpha$ than large drops (Eq. 1). Consequently small drops deform less than large drops, thereby widening the distribution and increasing its skewness. Quantitatively, the stretching of each droplet can be seen as the transformation of the random variable $h_0/{\ell }_c$ into $h/{\ell }_c$ following Eq. 3. For our purpose, Eq. 3 can be rewritten as $h/{\ell }_c=f_{\tilde{\alpha }}\left(h_0/{\ell }_c\right)$, a function of the initial random variable $h_0/{\ell }_c$ with a global parameter $\tilde{\alpha }=\rho g_{\mathrm{e}\mathrm{ff}}{\ell }_c/G$, the value of $\alpha$ for the most probable droplet in the initial distribution. It follows that $h_0/{\ell }_c=f_{\tilde{\alpha }}^{-1}\left(h/{\ell }_c\right)$, with $f_{\tilde{\alpha }}^{-1}$ the inverse function of $f_{\tilde{\alpha }}$. The final hair distribution can then be computed (36) from the initial log-normal distribution as

$${\mathcal{P}}_{\tilde{\alpha }}\left(\frac{h}{{\ell }_c}\right)={\mathcal{L}\mathcal{N}}_{\mu ,\sigma }\left(f_{\tilde{\alpha }}^{-1}\left(\frac{h}{{\ell }_c}\right)\right)\left|\frac{\partial f_{\tilde{\alpha }}^{-1}\left(h/{\ell }_c\right)}{\partial \left(h/{\ell }_c\right)}\right|.$$ [4]

We plot the theoretical evolution of the height distribution as we continuously increase $\tilde{\alpha }$ in Fig. 4F. We find that Eq. 4 predicts a positively skewed widening of the distribution as seen in the experiments. In Fig. 4 B–D we compare our model to experiments with VPS-8 hairs. The distributions obtained with our model are shown as solid curves and the value of $G$ is adjusted around $G^{\prime }\left({\tau }_g\right)\approx 40$ Pa (Fig. 1B) using a maximum-likelihood estimation (36). As evident from Fig. 4, there is a favorable agreement between our model and the experiment (Fig. 4 B and C). As expected from the analysis of individual hairs, the agreement worsens for $\tilde{\alpha }\gtrsim 8$ (Fig. 4D) owing to the limitations of our elastic model.

Shaping an Interface.

Using parameterized centrifugal acceleration, we have shown that liquid and elastic deformations could be coupled to produce a different kind of periodic structures in solidifying elastomer melts. Taking advantage of the continuously varying mechanical properties of the melt, we first form an initial droplet pattern via the liquid Rayleigh–Taylor instability. We then amplify the pattern by elastically stretching the drops into hairs when the elastomer is half cured. Albeit elastic in nature, the stretching of the half-cured polymer is eventually imprinted on the final material as cross-linking proceeds in the melt. When the substrate rotation is halted, the hairs remain in place and no noticeable deformation due to the lack of acceleration can be noticed. In fact, the elasticity of the elastomer is now orders of magnitude greater than when it has been stretched. This pattern is rationalized using the tools of both fluid and solid mechanics; the wavelength of the pattern is fixed by a fluidic instability through the capillary length ${\ell }_c$, while the amplitude of the pattern stems from elasticity and the acceleration jump $\alpha$.

Although demonstrated on a specific example, our approach is generic and can theoretically be applied to any material whose mechanical properties vary significantly. Examples include cooling melts, metals, and glass, but also programmable materials such as shape memory polymers that could make the pattern-forming process reversible. Using different types of forcing (e.g., vibrations, acoustic or electromagnetic waves) could unveil a variety of patterns that remain to be discovered, while using smart materials (e.g., dielectric elastomers, composites) could make these structures active in response to stimuli. These patterns could offer more flexibility than their single-step counterpart to build structured materials for applications in wave control, sensing, adhesion, or wetting. In addition, we believe our approach to modeling that consists of rationalizing the different pattern-forming processes individually and tying them together statistically to understand the final structure could be applied to multistep patterns formed by different physical processes involving seeding (e.g., via fracture, condensation, or crystallization).

Materials and Methods

Experimental Procedure.

Two silicone-based elastomers are used: VPS-8 (Zhermack Elite Double 8 with a weight base to catalyst ratio of 1:1) and PDMS (Dow Corning Sylgard 184 mixed with cure accelerator 3-6559 using the base:catalyst:accelerator weight ratios 8.4:1:1.66). The whole experiment is done at room temperature $T=21\pm 1\hspace{0.17em}°$C. The VPS-8 (resp. PDMS) reagents are mixed in a centrifuge (Thinky ARE-310) for 10 s (resp. 30 s) at 2,000 rpm clockwise and then 10 s (resp. 30 s) at 2,200 rpm counterclockwise. The end of mixing sets the zero of time for our experiments.

The initial coating is done by first pouring the melt on a horizontal cylinder of radius $R=63.6$ or $R=38.1$ mm attached to a spin coater (Laurell WS-650Mz-23NPPB). We then use a custom blade coater with a 1-mm gap to even out the initial thickness. For VPS-8 we start coating 1 min 10 s after mixing and subsequently start 1 min 30 s later the cylinder rotation at ${\mathrm{\Omega }}_1$. For PDMS, we degas the mixed reactant in vacuum for 6 min before starting the cylinder coating. The rotation at ${\mathrm{\Omega }}_1$ is subsequently started 2 min later. Finally the second rotation step at ${\mathrm{\Omega }}_2$ is triggered at $t^{*}$.

Material Properties.

The time-dependent rheology data of the curing elastomers are obtained through small-amplitude oscillation with an Anton Paar MCR 301 rheometer (using a cone-plate geometry CP25-1). Because the elastomers are curing rapidly, we cannot measure both the spectral and temporal responses simultaneously. We chose to measure {$G^{\prime }\left(t\right)$, $G^{{}^{″}}\left(t\right)$ } the storage and loss moduli as a function of time at a constant low strain ($\le 5\%$) and a constant frequency ($0.3\text{to}0.5$ Hz). This range of frequency is of the order of the maximal frequency imposed in our experiments which comes from the cylinder acceleration: The motor needs 3 to 5 s to change speed (Fig. 2A). The data for VPS-8 are shown in Fig. 1B while the data for PDMS are shown in SI Appendix, Fig. S1A.

These rheological measurements are restricted to small deformations and a narrow frequency range. Moreover, the curing reaction speed and hence ${\tau }_g$ of these materials are impacted by many external factors such as temperature, mixing ratios, or the flow within the melt (17). Since $G^{\prime }$ increases exponentially around the gelation point, the small experimental variations of ${\tau }_g$ create noticeable differences of shear modulus for a given $t^{*}$. As a result, we know only the order of magnitude of the shear modulus $G$ and have to calibrate it using the FEM simulations by matching the shape of a few drops as done in Fig. 2B.

The surface tensions of both elastomer melts are similar, $\gamma \approx 21$ mN/m, as well as their densities with ${\rho }_{\mathrm{V}\mathrm{P}\mathrm{S}-\mathrm{8}}=\mathrm{1,070}$ kg/${\mathrm{m}}^3$ and ${\rho }_{\mathrm{P}\mathrm{D}\mathrm{M}\mathrm{S}}=\mathrm{1,030}$ kg/${\mathrm{m}}^3$.

Image Analysis.

High-speed movies of the drops during stretching are recorded with either a Kron Technologies Chronos 1.4 or a Phantom v2012. The multistep stretching shown in Fig. 2 takes about 0.5 min while the cylinder velocity is variable and very high (up to 10.7 m/s). To extract as much information as possible from the limited memory of the camera, we record a small region of the cylinder shown in SI Appendix, Fig. S1C at a high frame rate and obtain a very large number of frames ($\sim 10^6$). We then extract a radial line of pixels from each frame and append them to construct a spatiotemporal image (or kymograph) that unwraps the whole experiment. The horizontal axis on this unwrapped image therefore represents both the time and the angular position on the cylinder. A mark on the cylinder allows us to detect each full rotation of the cylinder such that we can crop horizontally the full spatiotemporal image into multiple images, each representing one rotation. We finally resize horizontally each of these images to recover the original aspect ratio (the width of each image is set to $2\pi R$). This treatment reconstructs an unwrapped image of the whole cylinder perimeter that shows all of the drops side by side for each cylinder rotation (SI Appendix, Fig. S1C).

For the statistical analysis, pictures of the cured samples are taken with a high-resolution camera while rotating the sample (one picture every $10°$) to image a large number of drops/hairs. All our image analysis is done with imageJ and Matlab.

Simulations.

Two-dimensional axisymmetric finite-element simulations are performed with the commercial software COMSOL 5.4. First, the initial drop shape is computed by solving numerically the Young–Laplace equation with the appropriate boundary conditions (20) (Mathematica, shooting method):

$$\begin{array}{c}\frac{{\mathrm{d}}^2\theta \left(s\right)}{\mathrm{d}{s}^2}=\frac{-\cos \theta \left(s\right)}{{\ell }_c^2}+\frac{\mathrm{d}}{\mathrm{d}s}\left[\frac{\cos \theta \left(s\right)}{r\left(s\right)}\right]\\ \frac{\mathrm{d}z\left(s\right)}{\mathrm{d}s}=\cos \theta \left(s\right),\frac{\mathrm{d}r\left(s\right)}{\mathrm{d}s}=\sin \theta \left(s\right),\\ z\left(0\right)=0,\theta \left(0\right)=-\pi /2,\\ r\left(s_{\mathrm{f}}\right)=0,\theta \left(s_{\mathrm{f}}\right)=-\pi /2,z\left(s_{\mathrm{f}}\right)=h_0.\end{array}$$ [5]

Here, {$r\left(s\right)$, $z\left(s\right)$} are the (cylindrical) coordinates of the drop surface, $\theta \left(s\right)$ is the local angle that the tangent makes with the vertical, and $s$ is the arc length as defined in SI Appendix, Fig. S1B. The value of $s_{\mathrm{f}}$ is a priori unknown and is determined by the additional boundary condition.

The drop shapes are then imported in the FEM solver and a thin layer of material (height $0.05{\ell }_c$, width $\pi \sqrt{2}{\ell }_c$) is added below the drop to complete the simulated geometry: a unit cell of our experimental drop lattice including the thin film connecting the drops. We finally apply an effective gravity jump $g_{\mathrm{e}\mathrm{ff}}=R\left({\mathrm{\Omega }}_2^2-{\mathrm{\Omega }}_1^2\right)$ to the drop and solve for the static mechanical equilibrium with an incompressible neo-Hookean hyperelastic material model.

Data Availability

All study data are included in this article and/or SI Appendix.