Optimization of the Pore Structures of MOFs for Record High Hydrogen Volumetric Working Capacity

Abstract

Metal–organic frameworks (MOFs) are promising materials for onboard hydrogen storage thanks to the tunable pore size, pore volume, and pore geometry. In consideration of pore structures, the correlation between the pore volume and hydrogen storage capacity is examined and two empirical equations are rationalized to predict the hydrogen storage capacity of MOFs with different pore geometries. The total hydrogen adsorption under 100 bar and 77 K is predicted as n_tot = 0.085 × V_p − 0.013 × V_p² for cage-type MOFs and n_tot = 0.076 × V_p − 0.011 × V_p² for channel-type MOFs, where V_p is the pore volume of corresponding MOFs. The predictions by these empirical equations are validated by several MOFs with an average deviation of 5.4%. Compared with a previous equation for activated carbon materials, the empirical equations demonstrate superior accuracy especially for MOFs with high surface area (i.e., S_BET over ≈3000 m² g⁻¹). Guided by these empirical equations, a highly porous Zr-MOF NPF-200 (NPF: Nebraska Porous Framework) is examined to possess outstanding hydrogen total adsorption capacity (65.7 mmol g⁻¹) at 77 K and record high volumetric working capacity of 37.2 g L⁻¹ between 100 and 5 bar at 77 K.

The CO₂ emission from combustion of fossil fuel has caused serious environmental issues such as global warming. Hydrogen has been recognized as a promising candidate to replace fossil fuel because of its high energy density (33.3 kWh kg⁻¹),^[1] which is three times higher than that of gasoline (11.1 kWh kg⁻¹) and clean combustion that only produce water as by-product. In order to use hydrogen as fuel for automobiles, 5.6 kg of H₂ need to be stored safely and efficiently to allow 300 miles driving of fuel cell vehicle with each filling. Storage of hydrogen is very challenging due to its low density and requires compression of hydrogen at very high pressure of 700 bar. Such processes involve significant energy input and expensive carbon fiber tank.^[2]

Traditional porous adsorbents such as zeolites^[3] and carbon materials^[4] and emerging porous materials such as metal–organic frameworks (MOFs),^[5] covalent-organic frameworks (COFs),^[6] and microporous polymer^[7] have been studied to store hydrogen at lower pressure. MOFs constructed by connecting metal ion or cluster with organic linkers are highly tuneable materials in terms of their surface area, pore size, pore geometry, and functional sites^[8] and has demonstrated great potential for gas storage and separation.^[1,9] The well-defined structures also allow crystallography and computational studies of host–guest interaction to gain fundamental understanding for rational material design.^[10]

In 2003, Rosi et al.^[11] reported for the first time the H₂ adsorption of microporous MOF at high-pressure up to 20 bar. Since then, many MOFs have been examined for H₂ storage and great progress has been made. The storage capacities of some highly porous MOFs^[12] (>14 wt% under 70 bar, 77 K) are much higher than those of traditional porous materials such as zeolite and activated carbon (<7 wt%).^[3,13]

For onboard hydrogen storage for fuel cell vehicles, the minimum usable gas pressure is 5 bar and only the adsorption capacity between pressure of 100 and 5 bar is the usable as working capacity. Therefore, the ideal H₂ storage material should exhibit high capacity at 100 bar and low capacity at 5 bar. U.S. Department of Energy (DOE) has set the gravimetric and volumetric working capacity targets of 4.5 wt%; 30 g L⁻¹ (2020), 5.5 wt%; 40 g L⁻¹ (2025), and 6.5 wt%; 50 g L⁻¹ (ultimate).^[14] Although several MOFs such as NU-1103 (NU: Northwestern University), UMCM-9 (UMCM: University of Michigan Crystalline Material), and NU-100 possess high gravimetric working capacity reaching the DOE target, simultaneously high volumetric working capacity is still very challenging and the current record by NU-100 is only 35.5 g L⁻¹ between 100 and 5 bar at 77 K.

Working capacity involves two distinct adsorption conditions under which the correlations between adsorption capacity and pore properties are quite different. Understanding the adsorption behavior at high pressure is pivotal to obtain high working capacity and some research endeavours have been performed along this way. For example, the excess H₂ adsorption is found to be positively correlated with the MOF surface area.^[15] Such correlation is similar to what found previously for carbon materials.^[16] Indeed, H₂ excess adsorption of MOFs follows this correlation fairly well for those with surface area under ≈ 3000 m² g⁻¹.^[2c] For MOFs with higher surface area, the hydrogen adsorption falls off the trend,^[15a,17] which is likely caused by the decreased pore surface occupancy as the surface area and pore volume increase. Such phenomenon has been found in our previous study of high-pressure methane adsorption.^[9a,18] Besides, the structural properties of MOFs such as pore size, pore geometry, and aperture size significantly affect the gas adsorption behavior at high pressure.^[10a] Full consideration of structural properties can only be realized with extensive computational screening of a great number of MOFs.^[10c,15b] Our previous successful discovery of the correlation between pore volume and methane adsorption motivates us to explore such empirical equation for hydrogen adsorption with consideration of pore occupancy and pore geometry.

Theoretically, the sorbate–sorbent interaction potential in spherical pore is higher than that in cylindrical pore due to more surface atom interaction.^[19] Similarly for MOF materials, we speculate that the interaction potential in cages would be higher than that in channels, which would result in higher pore occupancy and adsorption capacity for cage-type MOFs. In this work, we analyzed a series of MOFs from the same measurements^[2c] to correlate the pore geometry with hydrogen total adsorption. We found that the cage-type MOFs generally possess higher pore occupancy than that of channel-type MOFs with the same pore volume. Accordingly, taking the pore geometry into accounts, empirical equations have been rationalized for the H₂ total adsorption prediction with given pore volume. Guided by these empirical equations, we discovered that a cage-type Zr-MOF NPF-200 (NPF: Nebraska Porous Framework)^[20] exhibits record high volumetric working capacity (37.2 g L⁻¹ at 77 K, 100–5 bar) and simultaneously high gravimetric working capacity.

In comparison of computational screening of millions of MOFs by machine learning^[15b] strategy, only limited number of MOFs were experimentally measured for H₂ storage. Our analysis starts from the MOFs measured under the same conditions^[2c] to minimize the inconsistency of measurements. To study the effects of structural properties to H₂ adsorption, the crystal structure of MOFs must accurately represent the bulk MOF material, which is not always the case since some MOFs are well known to contain significant amount of crystal defects^[21] or become partially collapsed during activation.^[22] Therefore, we compared the experimental pore volume and Brunauer–Emmett–Teller (BET) surface area with calculated pore volume and surface area, and large deviations (>10%) have been found for four MOFs as shown in Table S1 in the Supporting Information. We then excluded these four MOFs and used the other six MOFs: HKUST-1 (HKUST: Hong Kong University of Science and Technology), NU-125, NU-1000, UiO-68-Ant (UiO: University of Oslo; Ant: anthracene), Cu-MOF-74, and Zn₂(bdc)₂(dabco) for the following study.

The pore diameter (D), aperture size (A), and pore diameter to aperture size ratio (D/A) have been measured from their crystal structures. Based on the D/A ratio, these six MOFs can be categorized into two types: cage-type with large D/A ≈1.8 or higher and channel-type with D/A = 1 as shown in Figure 1a,–f and Table 1. We hypothesize that the cage-type MOFs would have stronger sorbate–sorbent interaction potential due to more surface atom interaction. Such hypothesis is based on theoretical calculation of interaction potential in cylindrical and spherical pore geometries. In spherical pore, more surface atoms are in close contact with the guest molecule, which lead to higher interaction potential as demonstrated in Figure S1 in the Supporting Information. Consequently, spherical pore can adsorb more guest molecules under unsaturated conditions, in another word, possess a higher pore occupancy. The closest model of ideal spherical pore is fullerene, while we speculate that the adsorption behavior of cage and channel in MOFs would to some extend follow the principle of spherical and cylindrical pores.

Figure 1.

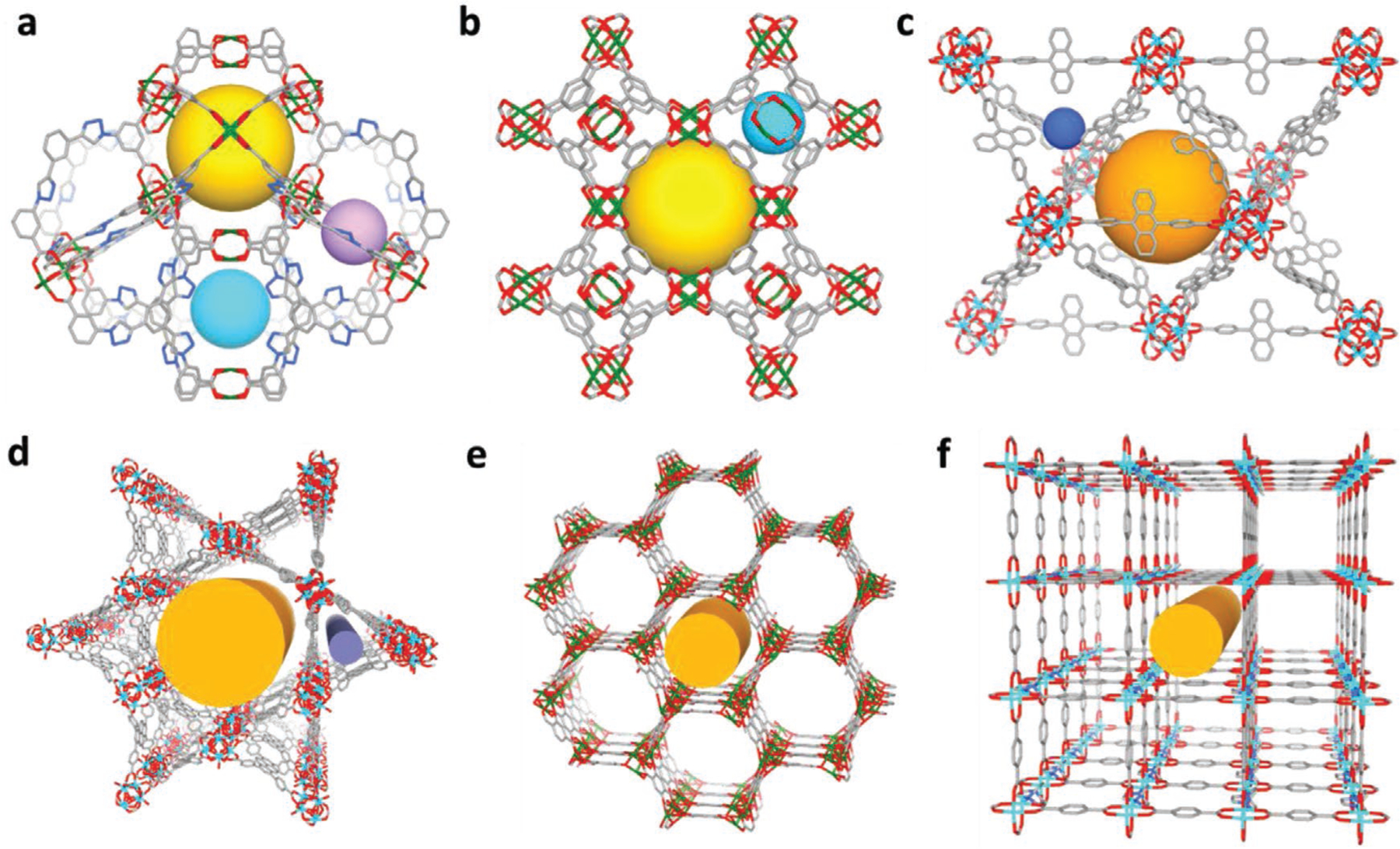
Major channels or cages in the investigated MOFs structures. a) NU-125, b) HKUST-1, c) UiO-68-Ant, d) NU-1000, e) Cu-MOF-74, and f) Zn₂(bdc)₂(dabco)₂.

Table 1.

Comparison of D (pore diameter) (cage or channel size is measured by fitting the largest sphere or cylinder inside the pore considering the Van der Waals radius of atoms), A (aperture), and D/A ratio of cage and channel in MOFs.

MOF	Cavity-1			Cavity-2			Cavity-3
	D [Å]	A [Å]	D/A ratio	D [Å]	A [Å]	D/A ratio	D [Å]	A [Å]	D/A ratio
NU-125	20	5.3	3.8	12	5.3	2.3	6.6	5.3	1.2
HKUST-1	12	6.5	1.8	5	4.1	1.2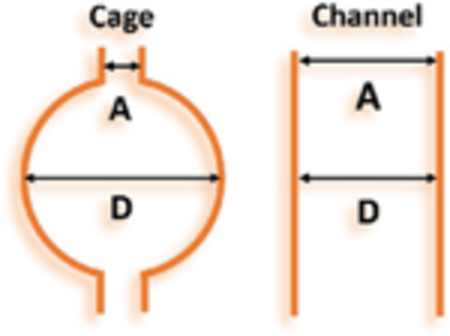
UiO-68-Ant	17	4	4.25	5	4	1.25
NU-1000	28.5	28.5	1	7.2	7.2	1
Cu-MOF-74	11	11	1
Zn2(bdc)2(dabco)	7.6	7.6	1	3.6 × 7.6	3.6 × 7.6	1

At very low temperature such as 30 K, the H₂ adsorption can reach saturation at about 4 bar, for MOF-5, and the H₂ packing density inside the pore is about 0.087 g cm⁻³, very close to the density of solid H₂ (0.086 g cm⁻³).^[18] Thus the saturated adsorption of hydrogen in MOFs can be estimated by equation: n_sat = ρ_solid × V_p, where n_sat is the saturated total adsorption, ρ_solid is the density of solid H₂, and V_p is the MOF pore volume. At higher temperature, such as 77 K, the adsorption cannot reach saturation even at high pressure of 100 bar. We can define pore occupancy, O, under 100 bar and 77 K, as total adsorption of H₂ under 100 bar and 77 K, n_tot, divided by saturated total adsorption n_sat (see Table S1, Supporting Information, for calculation details). As shown in Figure 2a and Table S2 in the Supporting Information, for both types of MOFs, the pore occupancy decreases as pore volume increases, which can be attributed to the lower interaction potential of adsorption in large pore center. The interaction potential decreases as the distance between H₂ molecule and the pore surface increases. For MOFs with high pore volume, the pore size is larger and the interaction potential of H₂ molecule in the pore center is mainly from the weak sorbate–sorbate interaction similar to the bulk gas. As expected, the pore occupancy of cage-type MOFs is higher than that of channel-type MOFs for MOFs in this study, such superiority of cage-type MOFs indicates that adsorption behavior of cage and channel in MOFs indeed follows the previously reported principle of spherical and cylindrical pores. Through data fitting, the pore occupancy is found to be approximately linearly related to the corresponding pore volume, for cage-type MOFs: O = 0.992–0.149 × V_p; for channel-type MOFs: O = 0.881 − 0.128 × V_p. Cross-validation of the fitting revealed the deviation is less than 1.0% which is much smaller than that of fitting all six MOFs in one group as shown in Tables S3 and S4 in the Supporting Information. Thus the total H₂ adsorption of a specific MOF can be calculated by the equation: n_tot = n_sat × O = (0.086 × V_p) × (0.992 – 0.149 × V_p) = 0.085 × V_p – 0.013 × V_p ² for cage-type MOFs; n_tot = n_sat × O = (0.086 × V_p) × (0.881 – 0.128 × V_p) =0.076 × V_p – 0.011 × V_p² for channel-type MOFs with units of g g⁻¹ for n_tot and cm³ g⁻¹ for V_p.

Figure 2.

a) Pore occupancy under 100 bar and 77 K versus pore volume (cm³ g⁻¹) of channel-type and cage-type MOFs. The dash lines show the linear fitting results. b) Predicted H₂ total adsorption under 100 bar and 77 K versus pore volume using our empirical equations for the two types of MOFs. Vertical line at 3.3 cm³ g⁻¹ indicates the peak total adsorption position. c) Comparison of predicted total adsorption with experimental adsorption of nine MOFs not used in empirical equation fitting. Prediction by our equation is closer to experimental adsorption (diagonal line). d) Comparison of deviations of prediction by our empirical equations and Chahine’s rule. The average deviation of the prediction by our empirical equation and by Chahine’s rule are 5.4% and 21.9%, respectively.

With the obtained empirical equations, the H₂ total adsorption at 100 bar and 77 K can be predicted with given pore volume. As shown in Figure 2b, the total adsorption would initially increase as the pore volume increases, until around pore volume of 3.3 cm³ g⁻¹. After that, the total adsorption starts to decrease due to the lower pore occupancy at higher pore volume region. Overall, the adsorption of cage-type MOFs is higher than that of channel-type MOFs with the same pore volume. The superiority of cage-type structure for gas adsorption has also been observed in pore space partition study when large channels are partitioned into cages.^[23] In reality, many MOFs would be somewhere between being purely cage-type and being purely channel-type. In this case, the two empirical equations predict a narrow range where the expected H₂ uptake might be located. To validate the prediction by these empirical equations, adsorption of another nine MOFs was predicted based on their structural type and compared with their experimental adsorption capacity (Figure 2c and Table S5, Supporting Information). The average deviation of the prediction is 5.4% indicating the reasonable accuracy of this method (Figure 2d). For comparison, the H₂ adsorption of these nine MOFs were also predicted using Chahine’s rule which states that the maximum excess adsorption can be predicted from the BET surface area (Scheme S1, Supporting Information). For activated carbon, the H₂ excess adsorption N_excess (wt%) = 1.91 × 10⁻³ × SA (m² g⁻¹) determined by fitting experimental data.^[16] In comparison with experimental adsorption and prediction by our equations (Figure 2c,d), the predictions of by Cahine’s rule yield large deviation for MOFs with high pore volume such as NU-1101 (30.2%) and NU-1103 (36.9%). The average deviation is 21.9%, much higher than that of our empirical equations (5.4%) as shown in Figure 2d. The superiority of our empirical equations indicates that the pore occupancy and pore geometry merit consideration especially for highly porous MOFs.

In practical application, the ideal material should also exhibit high volumetric adsorption capacity which requires high volumetric surface area for MOFs.^[10c] As shown in Table S6 in the Supporting Information, MOFs with ultrahigh pore volume such as NU-1301^[24] and DUT-60 (DUT: Dresden University of Technology)^[25] exhibits only small volumetric surface area. Considering the prediction results in Figure 2b, MOFs with moderately high pore volume of ≈3.3 cm³ g⁻¹ and high volumetric surface area would likely possess simultaneously high gravimetric and volumetric H₂ storage capacity at 100 bar and 77 K.

Base on the above analysis, we projected that a highly porous Zr-MOF NPF-200^[20] would be a promising candidate to balance the volumetric capacity and the gravimetric capacity, due to its near-optimal pore volume of 2.17 cm³ g⁻¹ and high volumetric surface area of 2268 m² cm⁻³. NPF-200 is considered as a cage-type MOFs since its largest cage with D/A ≈2 contributes the most to the total porosity, as shown in Figure 3a and Table S7 in the Supporting Information. The H₂ total capacity of NPF-200 was predicted to be 61.8 mmol g⁻¹ (11.7 wt%) based on the equation for cage-type MOFs. The H₂ excess and total adsorption of NPF-200 was predicted by Chahine’s rule as 55.7 and 89.4 mmol g⁻¹, respectively.

Figure 3.

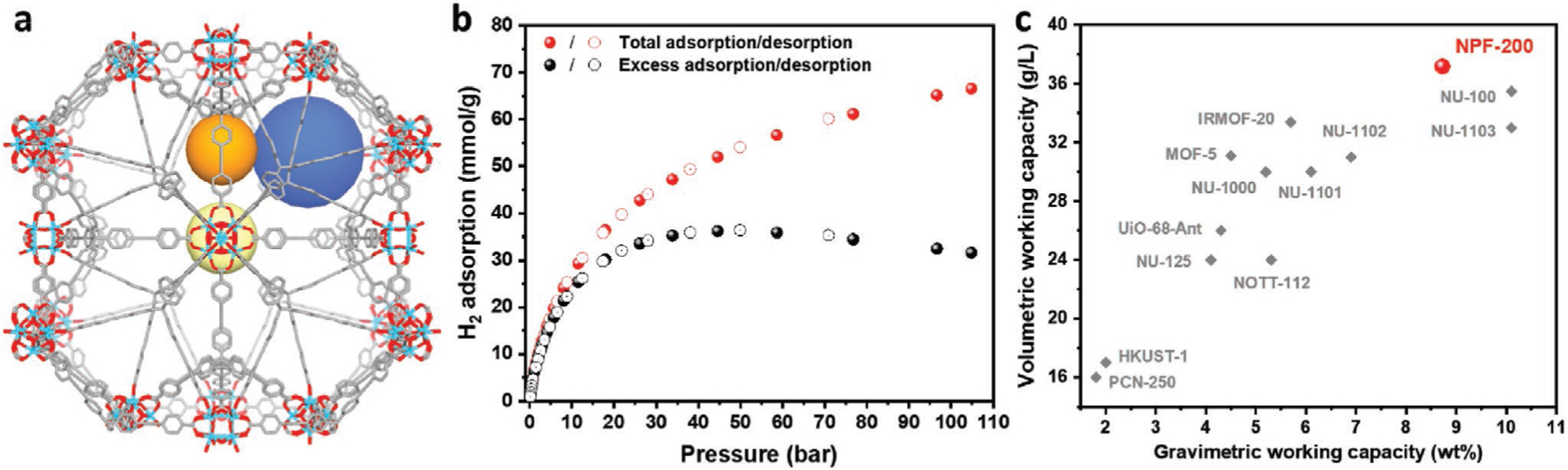
a) Three major cages of NPF-200. b) Hydrogen total and excess adsorption isotherm of NPF-200 up to 100 bar. c) Volumetric and gravimetric working capacity of NPF-200 between 100 and 5 bar at 77 K in comparison with the best MOFs reported to date.

The excess and total H₂ adsorption isotherms of NPF-200 were measured experimentally as shown in Figure 3b. The total adsorption at 77 K and 100 bar is 65.7 mmol g⁻¹ which is slightly higher than the predicted value of 61.8 mmol g⁻¹ by our empirical equation (with ≈5.9% deviation). In contrast, the predictions by Chahine’s rule overestimate the H₂ excess adsorption and total adsorption by 54% and 40%, respectively.

The total adsorption of NPF-200 is comparable to the best MOF materials such as NU-1102 (54.4 mmol g⁻¹), NU-1103 (73.9 mmol g⁻¹), MOF-210 (88 mmol g⁻¹), and NU-100 (82 mmol g⁻¹). The volumetric adsorption of NPF-200 (51 g L⁻¹) is also very high compared to the best MOFs reported such as NU-1102 (43.8 g L⁻¹), NU-1103 (44 g L⁻¹), MOF-210 (44 g L⁻¹), and NU-100 (49.7 g L⁻¹). The high gravimetric and volumetric adsorption of NPF-200 motivate us to further examine the gravimetric and volumetric working capacities which are 8.7 wt% and 37.2 g L⁻¹ respectively under 100 to 5 bar pressure swing condition at 77 K. To the best of our knowledge, the volumetric working capacity of NPF-200 is the highest among MOF materials under identical conditions as shown in Figure 3c and Table S8 in the Supporting Information. Meanwhile, its gravimetric working capacity is also quite high, only slightly smaller than those of NU-100 and NU-1103. NPF-200 represents a rare example of simultaneously high gravimetric and volumetric working capacities thanks to its near-optimal pore volume indicated by the empirical equation, cage-type pore geometry, and high volumetric surface area.

Lastly, the heat of adsorption (Q_st) was calculated from the adsorption isotherms at different temperatures (see Figure S4, Supporting Information). The initial Q_st of H₂ adsorption in NPF-200 is 4.5 kJ mol⁻¹, which is modest and similar to those of many other classical MOFs. It indicates that H₂ adsorption in NPF-200 is based on the typical van der Waals type interaction.^[2c,26]

In summary, we analyzed the contribution of pore geometry and pore occupancy to hydrogen total adsorption for a series of MOFs and rationalized two empirical equations to predict the total hydrogen adsorption under 100 bar and 77 K with given MOFs pore volume. Based on the prediction, cage-type MOFs with moderately high pore volume and high volumetric surface area seem to be promising candidates for hydrogen storage, which inspired our discovery of the cage-type Zr-MOF NPF-200 with simultaneously high volumetric and gravimetric working capacities. Especially, the volumetric working capacity (37.2 g L⁻¹) between 100 and 5 bar at 77 K of NPF-200 is the highest among reported MOFs. Considering its excellent structural and water stabilities,^[20] NPF-200 is a very promising material for practical H₂ storage application. Such encouraging result indicates that prediction based on our empirical equations could provide a quick guidance on MOFs evaluation and consequently accelerate the discovery of MOFs for high-pressure H₂ storage. It may also provide valuable guidance for H₂ storage using other types of porous materials such as covalent organic frameworks (COFs) and hydrogen bonded organic frameworks (HOFs). It is foreseeable that MOFs with higher storage capacity and working capacity will be discovered in the near future.

Experimental Section

Powder X-ray diffraction (PXRD) data were taken with a PANalytical Empyrean diffractometer with a PIXcel 3D detector. The copper target X-ray tube was set to 45 kV and 40 mA. N₂ adsorption isotherms at 77 K was measured under liquid nitrogen bath with Micromeritics ASAP (Accelerated Surface Area and Porosimetry System) 2020 surface area analyzer. High-pressure hydrogen sorption measurements were performed using a computer-controlled Sieverts apparatus, details of which can be found in a previous publication.^[27] Research grade hydrogen with purity of 99.999% was used for high-pressure measurements. PLATON^[28] was used to calculate the pore volume using a probe of 1.8 Å in radius, which corresponds to the kinetic diameter of N₂, to enable accurate comparison with experimental pore volume measured by N₂ adsorption at 77 K. Simulated BET surface area values are taken from ref. [2c]. Cage or channel size is measured by fitting largest sphere or cylinder inside the pore considering the Van der Waals radius of atoms.

For high-pressure studies, excess adsorption and total adsorption are frequently used to evaluate the gas storage capacity of porous material. Excess adsorption is approximately the amount of gas molecules interacting with pore surface. Total adsorption is the total amount of gas molecules inside the pore. Excess adsorption is determined experimentally and total adsorption is calculated with the following equation: n_tot = n_ex + ρ_bulk (P,T) × V_p, where ρ_bulk is obtained from the National Institute of Standardsand Technology (NIST) Refprop database^[29] and V_p is usually determined from the N₂ adsorption isotherm at 77 K. The H₂ density ρ_bulk = 15.528 mol L⁻¹ under 100 bar and 77 K. Weight percent (wt%) in this work is calculated by mass of H₂/(mass of H₂ + mass of material).

The structures and synthesis details of six MOFs (NU-125,^[30] HKUST-1,^[31] UiO-68-Ant,^[32] NU-1000,^[33] Cu-MOF-74,^[2c] and Zn₂(bdc)₂(dabco)^[34]) investigated for empirical formula derivation can be found in literatures.

Highly crystalline NPF-200 sample was synthesized and activated by supercritical CO₂ following the previously reported procedures.^[20] The PXRD and nitrogen adsorption match well with the previous measurements, indicating the phase purity and thorough activation of the sample. The measured pore volume is 2.17 cm³ g⁻¹, very close to the calculated value of 2.10 cm³ g⁻¹ by Platon. More details can be found in Figures S2 and S3 in the Supporting Information.