Experimentally determined strengths of favorable and unfavorable interactions of amide atoms involved in protein self-assembly in water

Significance

Quantitative information about strengths of amide nitrogen−amide oxygen hydrogen bonds and π-system and hydrophobic interactions involving amide-context sp² and/or sp³ carbons is needed to assess their contributions to specificity and stability of protein folds and assemblies in water, as well as to predict or interpret how urea and other amides interact with proteins and affect protein processes. Here we obtain this information from thermodynamic measurements of interactions between amide compounds in water and an analysis that determines intrinsic strengths of atom−atom interactions, relative to water and per unit area of each atom type present. These findings allow prediction or interpretation of effects of any amide on protein processes from structure, and may be useful to analyze protein interfaces.

Abstract

Folding and other protein self-assembly processes are driven by favorable interactions between O, N, and C unified atoms of the polypeptide backbone and side chains. These processes are perturbed by solutes that interact with these atoms differently than water does. Amide NH···O=C hydrogen bonding and various π-system interactions have been better characterized structurally or by simulations than experimentally in water, and unfavorable interactions are relatively uncharacterized. To address this situation, we previously quantified interactions of alkyl ureas with amide and aromatic compounds, relative to interactions with water. Analysis yielded strengths of interaction of each alkylurea with unit areas of different hybridization states of unified O, N, and C atoms of amide and aromatic compounds. Here, by osmometry, we quantify interactions of 10 pairs of amides selected to complete this dataset. An analysis yields intrinsic strengths of six favorable and four unfavorable atom−atom interactions, expressed per unit area of each atom and relative to interactions with water. The most favorable interactions are sp²O−sp²C (lone pair−π, presumably n−π*), sp²C−sp²C (π−π and/or hydrophobic), sp²O−sp²N (hydrogen bonding) and sp³C−sp²C (CH−π and/or hydrophobic). Interactions of sp³C with itself (hydrophobic) and with sp²N are modestly favorable, while sp²N interactions with sp²N and with amide/aromatic sp²C are modestly unfavorable. Amide sp²O−sp²O interactions and sp²O−sp³C interactions are more unfavorable, indicating the preference of amide sp²O to interact with water. These intrinsic interaction strengths are used to predict interactions of amides with proteins and chemical effects of amides (including urea, N-ethylpyrrolidone [NEP], and polyvinylpyrrolidone [PVP]) on protein stability.

Biopolymer self-assembly in water, including folding, binding, droplet formation, phase separation, and formation of the functional protein and nucleic acid complexes of the cell, is driven by net-favorable interactions between C, N, and O unified atoms of their biochemical functional groups, relative to interactions with water. To understand the energetics of these processes and relate thermodynamic and structural information, strengths of interaction of the different types of C, N, and O unified atoms with one another, relative to their interactions with water, must be determined. Effects of biochemical solutes and noncoulombic effects of salts from the Hofmeister series on these biopolymer processes result from preferential interactions of the C, N, and O atoms of the solute (and inorganic ions of the salt) with the C, N, and O atoms of the biomolecule (1, 2). Quantitative information about preferential interactions of the various types of C, N, and O atoms of biomolecules and solutes will therefore be useful in analyzing both self-assembly interactions and solute effects on these interactions.

Hydrogen bonding between amide sp²O and sp²N unified atoms (3–6) and the hydrophobic effect of reducing the exposure of sp²C and sp³C atoms to water (7–10) have long been recognized to be key determinants of specificity and stability of protein assemblies and complexes. In addition, n−π* interactions [a type of lone pair (lp)–π interaction (11)] between amide sp²O and amide or aromatic sp²C (12–17), π−π interactions of sp²C with sp²C (18, 19) and CH−π interactions of sp³C with sp²C (20–23) have been characterized by structural, spectroscopic, and computational studies. Much less is known about the relative strengths of these and other amide atom−atom contacts in water, including interactions of amide sp²N with amide sp²N, sp³C, and sp²C and interactions of amide sp²O with amide sp²O and sp³C.

Preferential interactions of biochemical solutes and Hofmeister salts with other solutes or biopolymers, relative to interactions with water, are quantified by chemical potential derivatives ${\left(\partial {\mathrm{\mu }}_2/\partial {\mathrm{m}}_3\right)}_{\mathrm{T},\mathrm{P},\mathrm{m}2}={\mathrm{\mu }}_{23}$ where the subscripts “2” and “3” refer to the two solutes and µ₂₃ = µ₃₂ (1, 2). These µ₂₃ values, related to transfer free energies, are determined by osmometry or solubility assays (20, 24–32). Integration of the radial distribution (33–36) of one solute in the vicinity of the other, obtained from molecular dynamics simulations (36–41), also yields µ₂₃ (31).

Experimental research and analysis extending over the last decade (24–32) has shown that µ₂₃ values are accurately described as a sum of contributions from interactions of solute 3 with the different types (hybridization states) of C, N, and O atoms on solute 2,

$$\hspace{0.17em}{\mu }_{23}={\displaystyle \sum _i{\alpha }_{3,i}AS{A}_{i\left(2\right)}}.$$ [1]

The choice of which solute to designate as component 2 or 3 is arbitrary because µ₂₃ = µ_32.

In Eq. 1, each intensive quantity ${\alpha }_{3,i}$ is a thermodynamic coefficient (called a one-way alpha value) that quantifies the strength of interaction of the amide compound designated component 3 (e.g., urea) with a unit area of one of the i different types of C, N, and O atoms on the set of amide compounds (each designated component 2), relative to interactions with water. The extensive quantity $AS{A}_{i\left(2\right)}$ in Eq. 1 is the water-accessible surface area (abbreviated ASA, in units of angstrom squared [Ų] where 1 Š= 0.1 nm), of the ith atom type of the amide solute (component 2) whose interaction with amide solute 3 is quantified by ${\mu }_{23}$. Examples of Eq. 1 for the interaction of two amide compounds investigated here are provided in SI Appendix, section III.

Eq. 1 is based on the two hypotheses that contributions to µ₂₃ from different weak solute−atom interactions are additive and increase in proportion to the ASA of that C, N, or O atom. Additivity has been tested and validated by analysis of sets of µ₂₃ values using Eq. 1 because the sizes of the µ₂₃ datasets greatly exceed the number of one-way alpha values determined from the analysis. ASA is found to be a better choice of extensive variable than the number of atoms or weighted number of atoms (31, 32). Using one-way alpha values ${\alpha }_{3,i}$, effects of solutes (species 3) on biopolymer (species 2) processes are predicted or interpreted in terms of the interaction of solute 3 with the different types of biopolymer ASA exposed or buried in the process.

The µ₂₃ values can be interpreted as free energy changes for transfer of a solute from a two-component solution to a three-component solution in which the concentration of the other solute is 1 molal. Originally, effects of urea and osmolytes on protein stability were interpreted assuming additivity of transfer free energy contributions from the peptide backbone and each of the nineteen different amino acid side chains that are exposed to the solution in unfolding (42–44). These 20 side chain and backbone transfer free energies were obtained from amino acid and dipeptide solubility data, also assuming additivity. Analysis of urea effects on protein stability using Eq. 1 involves many fewer parameters [from as few as two (45) to four (31) or seven (26, 27) one-way alpha values $\left({\alpha }_{urea,i}\right)$ depending on the extent of coarse graining of the ASA exposed in unfolding]. One-way alpha values are interpretable in terms of the local accumulation or exclusion of the solute in the vicinity of a particular type of atom on the model compound or protein, using the solute partitioning model (2, 20, 24–29, 46, 47).

Trends in one-way alpha values for interactions of the series of alkyl ureas with the different atoms of amide compounds (31) indicate that these one-way alpha values can be dissected further. This analysis, reported below, yields a set of 10 two-way alpha values quantifying strengths of all pairwise interactions (favorable and unfavorable) between the different types of unified C, N, and O atoms of amide compounds (amide sp²O, sp²N, sp²C; aliphatic sp³C) relative to water and per unit ASA of each atom. No experimental information of this type was previously available. These two-way alpha values are also useful to predict strengths of interaction of other amide compounds and the effects of amide compounds on protein processes like folding in which most of the change in ASA is from amide and hydrocarbon atoms. Our previous study focused on the series of alkylated ureas, all of which have small water-accessible surface area of amide sp²C atoms. Here we extend the amide dataset by determining µ₂₃ values for interactions of five other amides, including formamide and N-methylformamide, which have large amide sp²C ASA, and malonamide and N-acetylalanine N-methylamide (aama), which have two amide groups and correspondingly larger amide sp²O ASA.

Results

Analysis to Determine Atom−Atom Interactions from Solute−Atom Interactions.

For interactions of a series of urea and alkyl ureas (component 3) with amide compounds (component 2), analyzed by Eq. 1 as summarized above, each of the solute (3)−atom (i) one-way alpha values $\left({\mathit{\alpha }}_{3,\mathit{i}}\right)$ exhibited a regular progression with increasing alkylation (and reduced exposure of amide nitrogen) of the urea (SI Appendix, Fig. S1 and ref. 31). Motivated by this observation, here we test the hypothesis that each of these one-way alpha values can be dissected into additive, ASA-based contributions from the interaction of the different types of atoms on amide solute 3 (sp²O, N, C, and sp³C) with the ith type of atom (also sp²O, N, C, or sp³C) on amide solute 2.

$${\mathit{\alpha }}_{3,\mathit{i}}={\displaystyle \sum _{\mathit{j}}{\mathit{\alpha }}_{\mathit{ij}}\mathit{AS}{\mathit{A}}_{\mathit{j}\left(3\right)}}.$$ [2]

Eq. 2 for the one-way alpha value ${\alpha }_{3,i}$ is completely analogous to Eq. 1 for µ₂₃. In Eq. 2, each intensive quantity ${\alpha }_{ij}$ is the strength of interaction of a unit area of atom j of solute 3 with a unit area of atom i of solute 2, and the corresponding extensive quantity $AS{A}_{j\left(3\right)}$ is the accessible surface area of atom type j on solute 3. For the amide−amide interactions of interest here, an example with all of the individual terms in the sum in Eq. 2 is provided in SI Appendix, section III. The hypotheses of additivity and ASA dependence of the contributions ${\alpha }_{ij}AS{A}_{j\left(3\right)}$ to the one-way alpha value ${\alpha }_{3,i}$ are tested concurrently with the determination of two-way alpha values $\left({\alpha }_{ij}\right)$, because the number of equations (like Eq. 2) greatly exceeds the number of unknowns $\left({\alpha }_{ij}\right)$ being determined (see below). A direct but semiquantitative application of Eq. 2 to determine two-way alpha values from differences in one-way alpha values for amides differing primarily in ASA of one type of unified atom is given in SI Appendix, sections I and III and Eq. S1.

Combination of Eqs. 1 and 2 gives the proposed dissection of any solute−model compound µ₂₃ values into contributions from the interactions of accessible atoms of the solute with accessible atoms of the model compound,

$${\mathit{\mu }}_{23}={\displaystyle \sum _{\mathit{i}}{\displaystyle \sum _{\mathit{j}}{\mathit{\alpha }}_{\mathit{ij}}\mathit{AS}{\mathit{A}}_{\mathit{i}}\mathit{AS}{\mathit{A}}_{\mathit{j}}}},$$ [3]

where ${\alpha }_{ij}={\alpha }_{ji}$. The complete set of terms in this double sum for the amide compounds investigated here is given in SI Appendix, section III.

As an interpretation of one term in Eq. 3, consider the contribution to µ₂₃ from the interaction of amide sp²N of one amide solute (component 2) with amide sp²O on a second amide solute (component 3), relative to interactions with water, given by ${\alpha }_{sp2N-sp2O}AS{A}_{sp2N\left(2\right)}AS{A}_{sp2O\left(3\right)}$. The product of ASA values is proportional to the probability that a contact between the two solutes involves sp²N atom(s) of solute component 2 and sp²O atom(s) of solute component 3, and the two-way alpha value ${\alpha }_{sp2N-sp2O}$ is the strength of that interaction per unit ASA of both atom types, again relative to water. These two-way alpha values are useful to predict or interpret µ₂₃ values for interactions of amides for which one-way alpha values are not available, and to predict or interpret effects of these amides on protein processes in terms of structural information. Two-way alpha values may also be useful in analyses of atom−atom interactions in protein assemblies and in binding interfaces.

Vapor Pressure Osmometry Determinations of Interactions of Amides with Large ASA of Amide sp²C and sp²O.

Previously, we determined one-way alpha values ${\alpha }_{3,i}$ (Eq. 1) quantifying interactions of urea and six alkyl urea solutes with the types of unified atoms of amide (sp²O, sp²N, sp²C; sp³C) and aromatic hydrocarbon (sp²C) compounds using osmometric and solubility studies (31). Trends in these one-way alpha values with increasing alkylation of the urea showed which atom−atom interactions are favorable and which are unfavorable. However, preliminary tests of Eqs. 2 and 3 using the 95 ${\mu }_{23}$ values from this previous study revealed that these were insufficient to accurately quantify all atom−atom interactions (two-way alpha values) involving amide sp²O and/or sp²C.

Here we determine ${\mu }_{23}$ values by osmometry for an additional 10 interactions of five amide compounds, including interactions of two amides with large ASA of amide sp²C (formamide, N-methylformamide) with one another and with two amides with large ASA of amide sp²O (malonamide, aama). Interactions of these four amides with propionamide are also determined. In addition to their significance for the two-way analysis proposed here, these measurements also permit the determination of one-way alpha values for the interactions of these five amides with amide sp²O, sp²N, sp²C, and aliphatic sp³C atoms, increasing the number of amide compounds for which one-way alpha values (Eq. 1) are available from 7 to 12.

For uncharged solutes at concentrations up to ∼1 molal, the difference ΔOsm = Osm(m₂,m₃) – Osm(m₂) – Osm(m₃) between the osmolality (Osm) of a three-component solution and the two corresponding two-component solutions is proportional to the product of solute molal concentrations (m₂m₃) with proportionality constant μ₂₃/RT (31).

$$\mathrm{\Delta }\mathrm{Osm\hspace{0.17em}=\hspace{0.17em}}\left({\mathrm{\mu }}_{23}/\mathrm{RT}\right)\mathrm{\hspace{0.17em}}{\mathrm{m}}_2{\mathrm{m}}_3.$$ [4]

If ΔOsm is negative, μ₂₃ is negative, μ₂ decreases with increasing m₃, and the interaction of the two solutes is favorable.

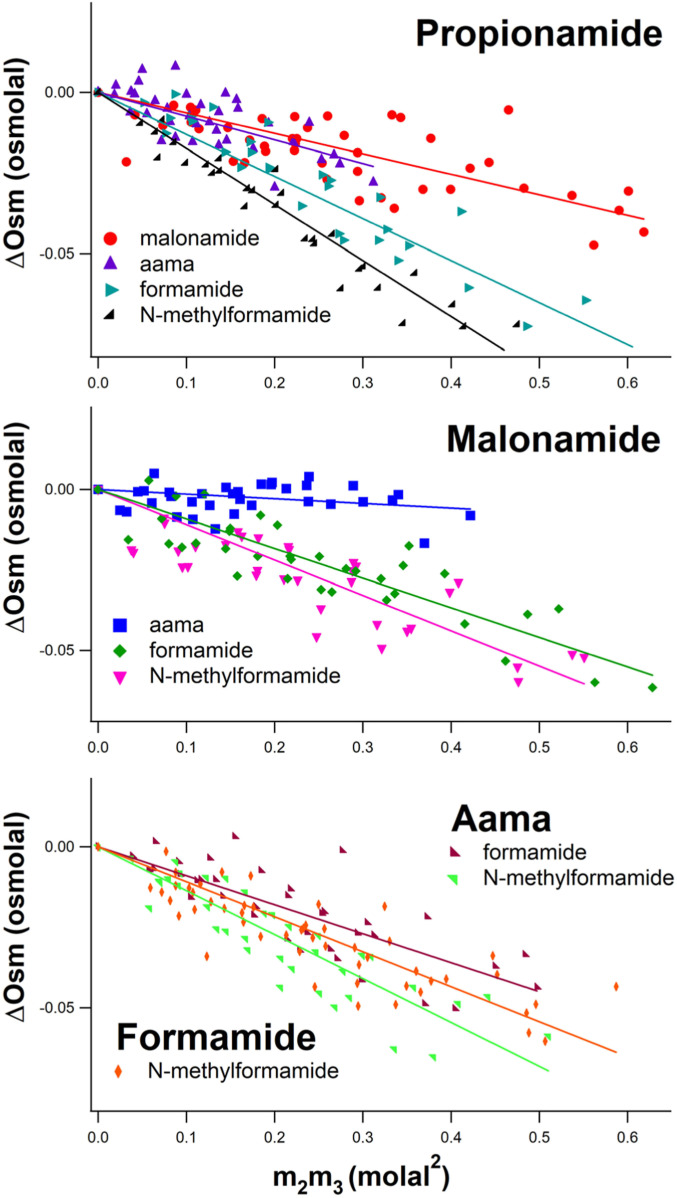
For each of the 10 pairs of amides investigated here, ΔOsm is plotted vs. m₂m₃ in Fig. 1. All µ₂₃ values are negative, indicating favorable interactions between all 10 pairs of amides investigated here. Values of µ₂₃ at 23 °C obtained from these slopes are listed in SI Appendix, Table S1. Of these, the interaction of malonamide and aama (Fig. 1, Middle) is the least favorable (µ₂₃ = −8.6 ± 2.2 cal⋅mol⁻¹⋅molal⁻¹), and the interaction of propionamide and N-methylformamide (Fig. 1, Top) is the most favorable (µ₂₃ = −102 ± 1.9 cal⋅mol⁻¹⋅molal⁻¹). Although there is substantial scatter in the data for some pairs of amides, slopes µ₂₃/RT are quite well determined (SI Appendix, Table S1) because the intercept is constrained to be zero.

Fig. 1.

Osmometric determinations of preferential interactions of pairs of amide compounds in water. (Top) Propionamide-amide interactions. (Middle) Malonamide-amide interactions. (Bottom) N-acetylalanine N-methylamide (aama)-amide and formamide-amide interactions. Osmolality differences $\mathrm{\Delta }\mathrm{Osm=Osm}\left({\mathrm{m}}_2,{\mathrm{m}}_3\right)-\mathrm{Osm}\left({\mathrm{m}}_2\right)-\mathrm{Osm}\left({\mathrm{m}}_3\right)$ between a three-component solution of two amide compounds and the two corresponding two-component solutions, determined by VPO at 23 °C, are plotted vs. the product of molal concentrations (m₂m₃) of the two amides (Eq. 4). Slopes of linear fits with zero intercept yield chemical potential derivatives ${\left(\partial {\mu }_2/\partial m_3\right)}_{P,\hspace{0.17em}\hspace{0.17em}T,m_2}=\hspace{0.17em}{\mu }_{23}$ quantifying preferential interactions between the two amides.

One-Way Alpha Values for Interactions of Five Amide Solutes with Amide O, N, and C Atoms.

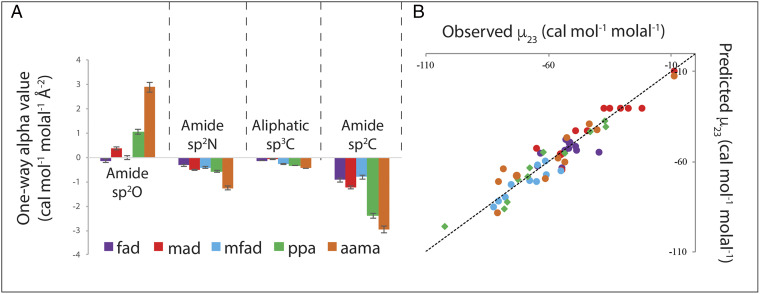
Analysis of the 10 µ₂₃ values determined from Fig. 1 together with previous results for the interactions of these five amides with other amides (31) by Eq. 1 yields one-way alpha values ${\alpha }_{3,i}$ for interactions of these five amides with each of the four types of unified atoms of amide compounds. These one-way alpha values are plotted as bar graphs in Fig. 2 and listed in SI Appendix, Table S2. SI Appendix, Fig. S1 compares one-way alpha value for all 12 amide compounds investigated to date. Fig. 2 and SI Appendix show that all amide compounds investigated here and previously interact favorably with amide sp²C, amide sp²N, and aliphatic sp³C, and that all but urea and formamide interact unfavorably with amide sp²O.

Fig. 2.

(A) Strengths of interaction of five amides (formamide [fad], N-methylformamide [mfad], malonamide [mad], propionamide [ppa] and N-acetylalanine N-methylamide [aama]) with amide and hydrocarbon unified atoms. Bar graphs compare interaction potentials (one-way alpha values; SI Appendix, Table S2) quantifying interactions of these five amide compounds with a unit area of amide sp²O, amide sp²N, aliphatic sp³C, and amide sp²C at 23 °C. Favorable interactions have negative one-way alpha values, while unfavorable interactions have positive one-way alpha values. (B) Comparison of predicted and observed µ₂₃ values for pairwise interactions of these five amide compounds at 23 °C. Predictions of µ₂₃ use one-way alpha values for these five amide compounds with amide sp²O, amide sp²N, amide sp²C, and aliphatic sp³ C from A and SI Appendix, Table S2. Color scheme is that of A. Observed µ₂₃ values are from SI Appendix, Tables S1 and S3. The line represents equality of predicted and observed values.

Strengths of Pairwise Interactions of Amide sp²O, N, C, and Aliphatic sp³C Unified Atoms.

All 105 µ₂₃ values (SI Appendix, Tables S3 and S4) for interactions of 12 different amide compounds with each other, and, in some cases, with naphthalene and/or anthracene, were analyzed using Eq. 3 to obtain 10 two-way alpha values (α_sp2O,sp2O, α_sp2O,sp2N, α_{sp2O, sp2C}, α_sp2O,sp3C; α_sp2N,sp2N, α_sp2N,sp2C, α_sp2N,sp3C; α_sp2C,sp2C, α_sp2C,sp3C; α_sp3C,sp3C). The previous one-way (31) analysis revealed that interactions of sp²C atoms of aromatic hydrocarbons and of amides are similar if not identical, and they are analyzed together here. Alternative analyses of sp²C presented in SI Appendix, section IV justify this treatment. In this analysis of all amide−amide and amide−aromatic µ₂₃ values, the number of equations (105 applications of Eq. 4) exceeds the number of unknowns (10 two-way alpha values) by more than 10-fold, making them highly overdetermined. The hypotheses of additivity and ASA dependence of the various atom−atom contributions to µ₂₃ underlying Eq. 3 are tested quantitatively by comparison of predicted and observed µ₂₃ values (SI Appendix, Tables S3 and S4 and Fig. 3B).

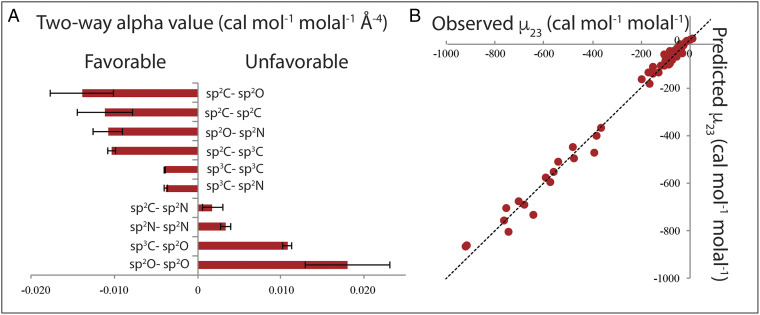
Fig. 3.

Amide compound atom−atom interaction strengths and their ability to predict µ₂₃ values. (A) Bar graph summary of two-way alpha values (Table 1) quantifying pairwise interactions of unified C, N, and O atoms of amide compounds, relative to interactions with water at 23 °C. (Sp²C is combined amide and aromatic sp²C.) Negative two-way alpha values indicate favorable interactions. (B) Comparison of predicted and observed µ₂₃ values for interactions of each pair of amide compounds investigated at 23 °C. Predictions of µ₂₃ use two-way alpha values in Table 1. Observed µ₂₃ values are from SI Appendix, Tables S1 and S3. The line represents equality of predicted and observed values.

Results of this analysis (two-way alpha values) quantifying the pairwise interactions of amide sp²O, sp²N, sp²C, and aliphatic sp³C unified atoms with one another are listed in Table 1. These 10 two-way alpha values are also plotted in the bar graph of Fig. 3A in ranked order from the most negative (most favorable interactions relative to interactions with water) to the most positive (most unfavorable interactions). Uncertainties in these two-way alpha values range from 3 to 30%, except for the small-magnitude interaction of sp²C with sp²N, where the uncertainty is larger (∼70%). These uncertainties do not affect the semiquantitative conclusions of this research.

Table 1.

Ranked intrinsic strengths of atom−atom interactions of amide compounds

Interaction Type	Amide atom*		Strength
	i	j	Two-way alpha value (cal⋅mol−1⋅molal−1⋅Å−4)	Relative to sp3C–sp3C
Aliphatic sp3C interactions:	sp3C	sp2C	−0.0103 ± 0.0005	2.6
	sp3C	sp3C	−0.0039 ± 0.0001	1.0
	sp3C	sp2N	−0.0038 ± 0.0002	1.0
	sp3C	sp2O	0.0108 ± 0.0005	(2.8)†
Amide sp2C interactions:	sp2C	sp2O	−0.0139 ± 0.0038	3.6
	sp2C	sp2C	−0.0111 ± 0.0033	2.9
	sp2C	sp3C	−0.0103 ± 0.0005	2.6
	sp2C	sp2N	0.0018 ± 0.0013	(0.5)†
Amide sp2O interactions:	sp2O	sp2C	−0.0139 ± 0.0038	3.6
	sp2O	sp2N	−0.0108 ± 0.0017	2.8
	sp2O	sp3C	0.0108 ± 0.0005	(2.8)†
	sp2O	sp2O	0.0181 ± 0.0051	(4.6)†
Amide sp2N interactions:	sp2N	sp2O	−0.0108 ± 0.0017	2.8
	sp2N	sp3C	−0.0038 ± 0.0002	1.0
	sp2N	sp2C	0.0018 ± 0.0013	(0.5)†
	sp2N	sp2N	0.0034 ± 0.0006	(0.9)†

^*Labels i and j are interchangeable, so only 10 of the 16 two-way alpha values listed are unique.

^†Unfavorable interaction strengths (indicated by parentheses) are expressed relative to the magnitude of the sp³C–sp³C interaction.

Six of the 10 atom−atom interactions in Table 1 are favorable, with negative two-way alpha values. The four most favorable interactions, of similar strength when expressed per unit area of each unified atom, are sp²O−sp²C, sp²C−sp²C, sp²O−sp²N, and sp²C−sp³C. Two-way alpha values for these four interactions are about 3 times more negative than two-way alpha values for sp³C−sp³C and sp³C−sp²N interactions. The most unfavorable interaction in this set is sp²O−sp²O. Sp²O−sp³C and sp²N−sp²N interactions are modestly unfavorable, while the sp²N−sp²C interaction is slightly unfavorable. The signs and relative magnitudes of these interaction strengths, relative to interactions with water, make good chemical sense, as discussed below. We therefore conclude that these two-way alpha values not only are useful to predict and interpret interactions of amide solutes and amide effects on protein processes but also have fundamental chemical significance for understanding the weak interactions that drive self-assembly.

Comparison of Observed µ₂₃ Values and One-Way Alpha Values for Amide Solutes with Predictions from Two-Way Alpha Values.

Fig. 3B compares observed µ₂₃ values for interactions of the series of urea and amide solutes with those predicted from two-way alpha values (Table 1) and ASA information (31) using Eq. 3. All these observed and predicted µ₂₃ values are listed in SI Appendix, Tables S3 and S4. For amide−amide interactions, predicted and observed µ₂₃ values are in good agreement within the combined uncertainties ($\pm \hspace{0.17em}1$ SD, typically 15%) for about 90% of the interactions investigated (94 out of 105).

SI Appendix, Tables S3 and S5 and Fig. S2 summarizes results of additional comparisons of observed and predicted µ₂₃ values and one-way alpha values for amide solutes investigated here. SI Appendix, Table S3 compares µ₂₃ values for interactions of five amides (formamide, malonamide, N-methylformamide, propionamide, and aama) determined here and previously (31) with predictions of µ₂₃ and µ₃₂ from one-way alpha values using Eq. 1. SI Appendix, Fig. S2 and Table S5 compares one-way alpha values obtained by analysis of sets of µ₂₃ values for amides using Eq. 1 with predictions from two-way alpha values (Table 1) using Eq. 2. In almost all cases, good agreement within the combined uncertainties is obtained.

Applications of Two-Way Alpha Values.

SI Appendix provides applications of two-way alpha values for amide atom−atom interactions to analyze effects of the amide urea and the polyamide polyvinyl pyrrolidone on protein stability and also discusses the potential use of these two-way alpha values in polymer solution thermodynamic analyses of processes like expansion and contraction of polyamide flexible coils and aggregation/droplet formation of intrinsically disordered polypeptides.

Discussion

Chemical Significance of Amide Two-Way Alpha Values.

Interactions of aliphatic sp³C with aliphatic sp³C, amide/aromatic sp²C, and amide sp²N and sp²O.

Interactions of aliphatic sp³C atoms of amide compounds with aliphatic sp³C, amide sp²C, and amide sp²N atoms of other amides are favorable, while interactions with amide sp²O are unfavorable, relative to interactions with water. Strengths (two-way alpha values) of these preferential interactions, expressed per unit area of each atom type (Table 1), span a wide range. These two-way alpha values are well determined from the global fitting, with uncertainties of 3 to 5%.

The preferential interaction of sp³C with sp²C, quantified per unit ASA of each atom type, is one of the four most favorable atom−atom interactions characterized here. This is often called a CH−π interaction, and should also involve a hydrophobic effect from the burial of sp³C and sp²C ASA when it occurs. From Table 1 two-way alpha values, the strength of a favorable sp³C−sp²C interaction is almost 3 times that of an sp³C−sp³C interaction, which is presumably driven by a hydrophobic effect from removing sp³C ASA from water. Interpreted most simply, this comparison indicates that the CH−π component of the favorable interaction of aliphatic sp³C with amide or aromatic sp²C contributes more than the hydrophobic component of this interaction.

Two-way alpha values in Table 1 also reveal that the sp³C−sp²N preferential interaction is about as favorable as the sp³C−sp³C interaction. Because sp²N unified atoms are expected to interact more favorably with water than sp³C atoms do, it follows that the intrinsic interaction of sp³C with sp²N (i.e., not relative to water) is more favorable than the intrinsic interaction of sp³C with sp³C.

The sp³C−sp²O interaction in water is highly unfavorable, with a two-way alpha value that is equal in magnitude and opposite in sign to the sp³C−sp²C interaction. An unfavorable interaction means that intrinsic interactions of the unified sp³C and sp²O atoms with water are more favorable than the intrinsic sp³C−sp²O interaction. The sp³C−sp²O interaction is unfavorable because the intrinsic interaction of water with sp²O is favorable while the intrinsic interaction of sp³C with amide sp²O is probably comparably unfavorable to its intrinsic interaction with water.

Amide/aromatic sp²C interactions.

From Table 1, interactions of amide/aromatic sp²C atoms with amide sp²O, aliphatic sp²C, and amide sp³C atoms of other amides are all very favorable, while interactions with amide sp²N are slightly unfavorable, relative to interactions with water. Overall, amide/aromatic sp²C atoms interact more favorably with the atoms of amide compounds than any other atom type in Table 1. These sp²C two-way alpha values are not as accurately known as sp³C two-way alpha values. Except for the sp²C−sp³C interaction (5% uncertainty), uncertainties are 27% for interactions with sp²O and sp²C and 70% for the very weak interaction with sp²N.

The sp²C−sp²O interaction is the most favorable interaction quantified here, with a two-way alpha value which is about 3 times as favorable as for hydrophobic sp³C−sp³C, which we take as a reference. In all likelihood, the sp²C−sp²O interaction is an n–π* interaction [one example of an lp–π interaction (11)] involving n-shell electrons of amide sp²O and the π-system of the amide group or aromatic ring, as characterized previously in structural and spectroscopic studies and molecular dynamics simulations (12–17). The observation that a single two-way alpha value quantifies this interaction for both amide and aromatic sp²C is a compelling argument for the use of ASA in this analysis. This two-way alpha value is very similar to that deduced from the one-way alpha value for the interaction of naphthalene with amide sp²O (31) (SI Appendix, Table S6). Water forms hydrogen bonds to amide sp²O atoms and presumably participates in an lp–π interaction with sp²C atoms, so the strength of the sp²O−sp²C interaction in Table 1 is relative to these competitive interactions involving water.

Comparison of two-way alpha values in Table 1 reveals that the sp²C−sp²C interaction is about as favorable, per unit area of each participant, as the sp²C−sp³C interaction discussed above. Therefore it is likely that the π–π component of the sp²C−sp²C interaction, expressed per unit area of each participant, is similar in strength to the CH−π interaction and contributes about twice as much as the hydrophobic effect to the favorable sp²C−sp²C interaction.

The unnamed interaction of amide/aromatic sp²C with amide sp²N is very marginally unfavorable. This interaction is not as favorable as the sp³C−sp²N interaction, probably because the intrinsic interaction of water oxygen lps with the sp²C π-system is more favorable than the interaction of water with sp³C. Even so, because it is only marginally unfavorable, there should be no significant free energy penalty for forming contacts between amide/aromatic sp²C and amide sp²N in a protein interface.

Amide sp²O interactions.

From Table 1, interactions of amide sp²O atoms with amide and aromatic sp²C and amide sp²N atoms are both very favorable, while amide sp²O interactions with aliphatic sp³C and amide sp²O are very unfavorable, relative to interactions with water. Uncertainties in these two-way alpha values are moderate, ranging from 5% for sp²O−sp³C to 28% for sp²O−sp²C and sp²O−sp²O.

The favorable interaction of amide sp²O with amide/aromatic sp²C is discussed above. The similarly favorable interaction of amide sp²O with amide sp²N in water is almost certainly the NH···O=C hydrogen bond interaction in which the unified amide sp²N atom is the donor and the sp²O atom is the acceptor (3–6). The amide sp²O−amide sp²O interaction is almost twice as unfavorable as the amide sp²O–aliphatic sp³C interaction, because of the very favorable intrinsic interaction of amide sp²O with water, which contributes twice as much in magnitude to the two-way alpha value for sp²O−sp²O as for sp²O−sp³C.

Amide sp²N interactions.

From Table 1, the amide sp²N−amide sp²O interaction is the most favorable interaction involving amide sp²N, while the amide sp²N−aliphatic sp³C interaction is modestly favorable, and the amide sp²N interactions with amide/aromatic sp²C and amide sp²N is slightly unfavorable, relative to interactions with water. Uncertainties in two-way alpha values for interactions involving amide sp²N are small (5 to 18%) except for the very weak interaction with sp²C. All these interactions except amide sp²N−amide sp²N are discussed above.

The amide sp²N−amide sp²N interaction, which very likely is the NH···N hydrogen bond, is modestly unfavorable, indicating that hydrogen bonding of amide sp²N with water is intrinsically more favorable. Consistent with this, NH···N hydrogen bonds are seldom observed in protein secondary structures, except involving proline (48). However, a hydrogen bond between unified N atoms of heterocyclic aromatic rings occurs in both AT (also AU) and GC base pairs of nucleic acid duplexes.

Conclusion

Average strengths of interaction of amide O, N, and C unified atoms, quantified per unit of accessible area of each atom by two-way alpha values, provide important bridges between protein structural (ASA) information, molecular dynamics simulations, and experimental studies of protein−solute interactions and solute effects of protein processes, as well as a window into a chemistry of weak interactions of these O, N, and C unified atoms in water.

Materials and Methods

Details about materials, vapor pressure osmometry (VPO) measurements, and data analysis (determination of μ₂₃, surface area calculations) are provided in SI Appendix, section V and ref. 31.

Data Availability.

All study data are included in the article and SI Appendix.