Abstract
Motivation
Neuroimaging genetics is an emerging field to identify the associations between genetic variants [e.g. single-nucleotide polymorphisms (SNPs)] and quantitative traits (QTs) such as brain imaging phenotypes. However, most of the current studies focus only on the associations between brain structure imaging and genetic variants, while neglecting the connectivity information between brain regions. In addition, the brain itself is a complex network, and the higher-order interaction may contain useful information for the mechanistic understanding of diseases [i.e. Alzheimer’s disease (AD)].
Results
A general framework is proposed to exploit network voxel information and network connectivity information as intermediate traits that bridge genetic risk factors and disease status. Specifically, we first use the sparse representation (SR) model to build hyper-network to express the connectivity features of the brain. The network voxel node features and network connectivity edge features are extracted from the structural magnetic resonance imaging (sMRI) and resting-state functional magnetic resonance imaging (fMRI), respectively. Second, a diagnosis-aligned multi-modality regression method is adopted to fully explore the relationships among modalities of different subjects, which can help further mine the relation between the risk genetics and brain network features. In experiments, all methods are tested on the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database. The experimental results not only verify the effectiveness of our proposed framework but also discover some brain regions and connectivity features that are highly related to diseases.
Availability and implementation
The Matlab code is available at http://ibrain.nuaa.edu.cn/2018/list.htm.
1 Introduction
Alzheimer’s disease (AD), the most common form of dementia, is characterized by an insidious decline in memory, later affecting language, visuospatial perception, arithmetic abilities and executive functioning. Effective prevention and early diagnosis are the important research topic for AD (Brookmeyer et al., 2007; Winkler et al., 2010). At present, brain imaging genetics is an emerging field to study the influence of genetic variation on the brain structure and function (Ge et al., 2013; Glahn et al., 2007). Its major task is to examine the association between genetic markers such as single-nucleotide polymorphisms (SNPs) (The Genomes Project Consortium, 2015) and quantitative traits (QTs) extracted from multi-modal neuroimaging data (e.g. anatomical, functional and molecular imaging scans).
In the association analysis of imaging genetics, pairwise univariate analysis (Shen et al., 2010) is of extensive research. Meanwhile, regression analysis and bi-multivariate analyzes have also achieved very ideal results for exploring the joint effect of multiple SNPs on single or few QTs and revealing complex multi-SNPs-multi-QTs associations (Shao et al., 2018; Zhu et al., 2018; Zille et al., 2017). Most of these methods focus on the association analysis of neuroimaging and genetic variation based on brain structures. For example, Yan et al. (2014) have applied prior knowledge sparse canonical correlation analysis to the association between the APOE gene and structure information of 78 regions of interests (ROIs). Hao et al. (2016) have discovered common ROIs that are associated with both risk genetic factors and disease status by the multi-modal fusion technology. Du et al. (2016) have utilized a structured sparse canonical correlation method to analyze imaging genetic association. Based on this, they use a graph-guided fused lasso to conduct feature selection and feature grouping simultaneously. Song et al. (2016) have constructed functional networks between genes by the support vector machine classifier. Furthermore, the association between genes and diseases is rearranged.
At present, most of the methods regard each brain region as a single node, which ignores the interconnected signals between the nodes. Recent studies have shown that resting networks (RSNs) consist of internal functional connections by fluctuating coupling signals. The networks can be extracted from resting fMRIs to quantify brain region connections. They are also used to assess the association between a single region and other regions in a networked cluster. Meanwhile, the brain network connections of different individuals reflect the comprehensive characteristics of different brain systems (Sporns, 2014). In addition, the brain network model is a simple functional structural representation of the entire brain. However, the function interconnections between nodes are important data to constitute the entire network model and show the connection strength between the brain regions, for carrying different difference information between the patients and normal control (NC). For example, Fu et al. (2015) have obtained the conclusion that the functional connectivity of the human brain is genetically restricted by heritability analysis. At the same time, this gene level regulation is heterogeneous in different resting state functional networks. Jie et al. (2014) proposed a classification method based on the connection network to classify patients with mild cognitive impairment (MCI) and normal people, which can significantly improve the classification accuracy. Hence, the brain function connection network is closely related to genes and diseases.
In this article, a novel diagnosis-aligned multi-modality method is proposed to mine network phenotype between genetic risk factors and disease status. The novel imaging genetic association framework considers both network voxel node information and network edge connectivity information as intermediate traits that bridge genetic risk factors and disease status. In detail, the proposed method consists of two steps: (i) Extract the brain network features. The sparse representation (SR) model is used to build hyper-network to express the connectivity features of the brain. The network voxel node features and network connectivity edge features are respectively extracted from the structural magnetic resonance imaging (sMRI) and resting-state functional magnetic resonance imaging (fMRI). (ii) Mine network phenotype between genetic risk factors and disease status via the diagnosis-aligned multi-modality method. Most of existing multi-modality methods can select more discriminative features by embedding complementary information between multi-modality data. However, the traditional multi-modality regression methods only consider the relationship between the modalities of the same subjects. They neglect the potential internal relations among different modalities of different subjects. Therefore, a diagnosis-aligned multi-modality method is adopted to fully explore the relationships among different modalities of different subjects, which can help further mine the relation between the well-known AD risk SNP APOE rs429358 and two brain network features (i.e. network voxel node features and network connectivity edge features). As demonstrated in the experimental results, the proposed algorithm achieves much improved cross-validation performances as well as biologically meaningful results compared with the current state-of-the-art methods.
The contributions of this article are listed in the following two aspects:
A brain imaging genetics study can be performed to explore the relationship between brain network features and the well-known AD risk SNP APOE rs429358. This study is an initial attempt to explore the relationship between the connectivity features and genetic variants.
Adding the diagnosis-aligned regularization term can fully explore the relationships among different modalities of different subjects.
The rest of this article is organized in the following fashion. Section 2 presents our novel framework to mine network phenotype between genetic risk factors and disease status. Related simulation and experimental results are included in Section 3. Limitations and conclusions are given in Sections 4 and 5.
2 Materials and methods
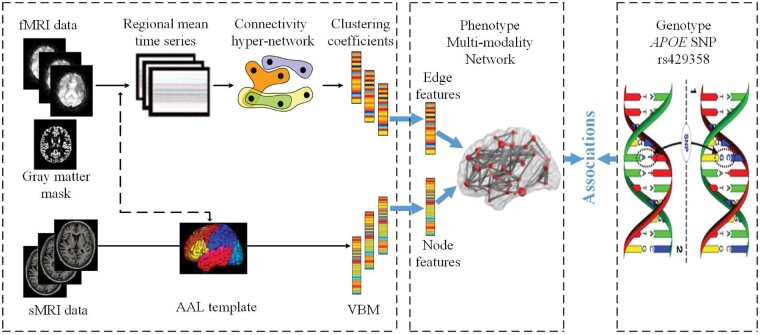
Recently, most of the current studies focus only on the associations between brain structure imaging and genetic variants, while neglecting the connectivity information between brain regions. In addition, the brain itself is a complex network and the higher-order interaction may contain useful information for the mechanistic understanding of diseases (i.e. AD). As the input, the brain fMRI and sMRI for each subject are then parcellated into 90 ROIs (remove the cerebellum) based on the Automated Anatomical Labeling (AAL) atlas. Figure 1 shows an overview of the proposed method. First, a SR model is adopted to build hyper-network to express the connectivity features of the brain, and the network voxel node features and network connectivity edge features are extracted from sMRI and fMRI. Second, a diagnosis-aligned multi-modality method is proposed to explore the relationship between the well-known AD risk SNP APOE rs429358 and two brain network features.
Fig. 1.
Overview of our proposed method
In the next subsection, we describe the hyper-graph, connectivity edge features and node features of the brain, multi-modality network phenotype associations, diagnosis-aligned multi-modality network phenotype associations and optimization algorithm.
2.1 Hyper-graph
It is known that a graph is a powerful tool for representing the pairwise relationships between paired nodes. Actually, besides pairwise relationships, in many applications (e.g. functional connectivity among brain regions), there may exist higher-order relationships, which cannot be represented by the conventional graphs. To overcome this problem, a hyper-graph has been proposed to characterize the higher-order relationship among nodes. In general, the hyper-graph is an extended graph where an edge (called hyper-edge in hyper-graph) can connect more than two nodes.
Denote a hyper-graph (Zhou and Huang, 2006) with a node set V and a hyper-edge set E, we can represent G using a incidence matrix H with elements 0 and 1 as follows:
| (1) |
where is a node and is a hyper-edge of G. Then, the node degree d(v) represents the number of hyper-edges passing through this node. The hyper-edge degree represents the number of nodes contained in this hyper-edge. They are defined as following:
| (2) |
| (3) |
It is worth noting that the conventional graph is a special kind of hyper-graph with each hyper-edge containing only two nodes. Figure 2 illustrates an example of a hyper-graph.
Fig. 2.
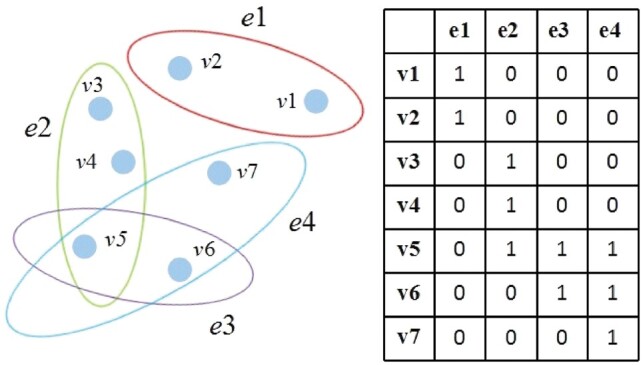
An example of the hyper-graph. Left: a hyper-graph in which each hyper-edge can connect more than two nodes. Right: the incidence matrix for the hyper-graph in the left
2.2 The connectivity edge features and node features of the brain
Inspired by the definition of the hyper-graph (in Section 2.1), in Jie et al. (2014, 2016), the authors use fMRI time series and the SR model to build the super-network as:
| (4) |
where zt represents the regional mean time series of the tth ROI. denotes a data matrix including all-time series except the tth ROI (where we put a vector of all zeros in its location). at is the weight vector that quantifies the degree of influence of other ROIs to the tth ROI. is a regularization parameter controlling the sparsity of the model.
In Gallagher and Goldberg (2013), the concept of the clustering coefficient has been extended from the conventional network to hyper-network, which reflects local clustering properties of the hyper-network. Therefore, after constructing the connectivity hyper-network by (4), the clustering coefficient of the hyper-network is completed by:
| (5) |
where HCC represents the amount of overlaps among adjacent hyper-edges of the node v. represents a set of hyper-edges adjacent to the node v. are the nodes that are neighbors of the node v. The numerator of (5), the difference between and , represents the number of vertices in multiple hyper-edges incident to v. The denominator represents the possible number of such overlaps.
Finally, for the definition of the clustering coefficients in (5), we extract a set of clustering coefficients from the connectivity hyper-networks as the connectivity edge features of the brain, hence, producing one set of connectivity edge features for each subject.
Otherwise, the voxel-based morphometry (VBM) is obtained by preprocessing sMRI data, which is the normalized gray matter density maps in the standard Montreal Neurological Institute (MNI) space as mm3 voxels. Then, we align the VBM to each subject’s same visit scan, and 90 ROIs (remove the cerebellum) level measurements of mean gray matter densities are further extracted based on the AAL atlas. In this article, we regard each ROI as a single node, thus, producing one set of node features for each subject.
2.3 Multi-modality network phenotype associations
Intuitively, pathological changes are closely related to the associated ROI and important network edges. The structural voxel features (i.e. VBM) from sMRI and the clustering coefficients in (5) from the fMRI can be considered as the network node and edge features. Then, we assume that there are N training subjects or samples, with each one represented by network node feature and network connectivity edge feature modalities of phenotypes. Given the network phenotypes as the input and the corresponding response value (i.e. APOE SNP rs429358) as the output, where d is the number of network QT (node and edge features dimensionality). Thus, the multi-modality network phenotype association model can be formulated as:
| (6) |
where is the linear discriminant function corresponding to the mth modality. is the weight matrix whose row wj is the vector of coefficients assigned to the jth feature across different modalities, and is a ‘group-sparsity’ regularizer, which penalizes all coefficients in the same row of the matrix W for joint feature selection. The parameter λ is a regularization parameter that is used to balance the relative contributions of those two terms in (6).
2.4 Diagnosis-aligned multi-modality network phenotype associations
One limitation of the traditional multi-modality models is that only the relationship between modalities of the same subjects is considered, while ignoring the important relationship among the different subjects with diagnostic information, i.e. NC, SMC, EMCI, LMCI or AD. To address this issue, we introduce a new diagnosis-aligned regularization term Ω, which minimizes the distance between within-class subjects in the projected space as follows:
| (7) |
where Sij is defined as:
| (8) |
where measures the distance between and in the projected space. It implies that if and are from the same class, the distance between them should be as small as possible in the projected space. Otherwise, when p = q, the local geometric structure of the same modality data is preserved in the projected space; when p < q, the complementary information provided from different modalities is used to guide the estimation of the projected space. Therefore, (7) preserves the intrinsic diagnostic information relatedness among multi-modality data and also explores the complementary information conveyed by different modalities. In general, the goal of (7) is to reserve diagnostic information relatedness by aligning paired within-class subjects from multiple modalities.
By incorporating the regularizer (7) into (6), we can obtain the objective function of our diagnosis-aligned multi-modality network phenotype association model as below:
| (9) |
where λ1 and λ2 denote control parameters of the regularization terms, respectively. Their values can be determined via inner cross-validation on training data. From (9), we can not only jointly select a subset of common features from multimodality data, but also retain diagnostic information relatedness by aligning paired within-class subjects. Figure 3 illustrates the used relationships among different modalities and subjects in our proposed method as compared with the traditional multi-modality methods. In Figure 3a, traditional multimodal methods only concern the single line relationships connecting node features and edge features of different modalities from the same subject. However, as shown in Figure 3b, our proposed model can preserve both the multi-modality relationship from the same subject and the correlation across modalities among different subjects. Moreover, when p = q, (9) will degenerate into the diagnosis-guided multi-modality model (Hao et al., 2016), which shows that (9) has a more general application scene.
Fig. 3.
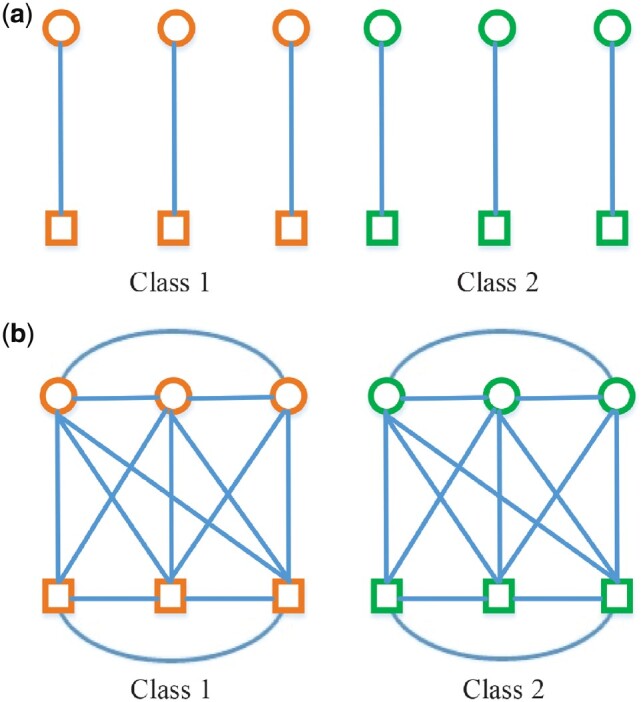
Illustrations on the relationships among modalities and subjects. (a) Traditional multi-modality method in identifying subjects for class 1 and class 2. (b) Proposed method in identifying subjects for class 1 and class 2. Circles and rectangles represent node features data from sMRI and edge features data from fMRI, respectively. Orange and green denote different classes
2.5 Optimization algorithm
A similar model has been used in Jie et al. (2015) and Zu et al. (2016) for multi-modality disease classification. Here, we also choose the widely applied accelerated proximal gradient (APG) method (Chen et al., 2009) to get the solution of our proposed method. First, we separate the objective function into the smooth part f(W) and non-smooth part g(W) as following:
| (10) |
| (11) |
Then, we define the approximation function as:
| (12) |
where denotes the gradient of f(W) on point Wi at the ith iteration, is Frobenius norm, l is the step size. Finally, the APG update step is as follows:
| (13) |
where wj and vj respectively denote the jth row of the matrix W and V, with
| (14) |
Therefore, through (13), this optimization problem can be decomposed into d sub-problems. The key of the APG algorithm is how to solve the update step efficiently. The analytical solutions of those sub-problems can be easily obtained by:
| (15) |
Instead of the gradient descent based on Wi via:
| (16) |
with
The optimization procedure of the proposed algorithm is shown as Algorithm 1.
Algorithm 1
Input:
Risk genetics (i.e. APOE SNP rs429358);
;
fMRI, sMRI data;
Subjects with diagnosis information (i.e. NC, SMC, EMCI, LMCI or AD).
Output:
Wk;
1. Extract voxel node features and network connectivity edge features from sMRI and fMRI data;
2. Get multi-modality network phenotype ;
3. Initialization: ;
4. For i = 1 to max iteration I
Compute Qi by (16)
While
Compute using (13)
End.
3 Experiments
In this section, we evaluate the performances of our method on ADNI dataset.
3.1 ADNI dataset
The imaging data (sMRI, fMRI) and genotyping data used in the preparation of this article were obtained from the Alzheimer’s disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 as a public–private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. For up-to-date information, see www.adni-info.org.
ADNI is the result of efforts of many coinvestigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the United States and Canada. The initial goal of ADNI was to recruit 800 adults, aged 55–90, to participate in the research approximately 200 cognitively normal older individuals to be followed for 3 years, 400 people with MCI to be followed for 3 years and 200 people with early AD to be followed for 2 years. In current studies, the subjects data used in this article includes two parts, one is fMRI and sMRI image data, and the other is SNP data. The mini-mental state examination (MMSE), which is neuropsychological assessment measures from different aspects, is often used as quantitative descriptions of symptom severity instead of binary diagnosis. After aligning the gene and imaging subjects and rejecting subjects with missing values, we used a total of 157 valid subjects, which include 38 NC, 19 significant memory concern (SMC), 40 early mild cognitive impairment (EMCI), 34 late mild cognitive impairment (LMCI) and 26 AD. Demographic information of the subjects is listed in Table 1.
Table 1.
Characteristics of the subjects
| Subjects | NC | SMC | EMCI | LMCI | AD |
|---|---|---|---|---|---|
| Number | 38 | 19 | 40 | 34 | 26 |
| Gender (male/female) | 15/23 | 7/12 | 17/23 | 22/12 | 11/15 |
| Age (mean ± SD) | 75.16 ± 7.64 | 72.41 ± 7.64 | 71.2 ± 7.58 | 71.85 ± 7.58 | 72.54 ± 7.64 |
| Education (mean ± SD) | 16.37 ± 2.68 | 16.63 ± 2.70 | 15.83 ± 2.68 | 16.85 ± 2.68 | 15.50 ± 2.69 |
| MMSE | 28.76 ± 1.27 | 29.05 ± 0.89 | 28.03 ± 1.74 | 27.85 ± 1.56 | 22.42 ± 2.44 |
Note: NC, normal control; SMC, significant memory concern; EMCI, early mild cognitive impairment; LMCI, late mild cognitive impairment; AD, Alzheimer’s disease; MMSE, mini-mental state examination.
3.2 Experimental setup
We use the root-mean-squared error (RMSE) and correlation coefficient (CC) between actual and predicted response values to measure the performance of regression and association analysis.
In the experiments, we have conducted the centering preprocessing for the node, edge features and response valuable y in the training set. The 5-fold cross-validation strategy is implemented in the training dataset to tune the free parameters and evaluate the effectiveness of our proposed method. The regularization parameter μ in the SR model is tuned from . As for regularization parameters of the regression and association analysis, we tune the parameters λ1, λ2 in the proposed DAMM model [i.e. shown in (9)] both from . Besides, in the optimization algorithm, the larger values of σ and l0 usually come with the faster convergence speed, and we set l0 and σ as 1 and 2, respectively.
We compare SM [denoted as single modality-based method with Lasso (Tibshirani, 2011) to detect a sparse significant subset from node features or edge features], MM (denoted as multi-modality method to detect a sparse subset of common ROIs from node features and edge features), DGMM [denoted as multi-modality-based method with diagnosis-guided (Hao et al., 2016) to detect a sparse subset of common ROIs from node features and edge features] and DAMM (denoted as multi-modality-based method with diagnosis-aligned to detect a sparse subset of common ROIs from node features and edge features).
3.3 Improved association between risk SNP and network phenotype
We compare our proposed DAMM method with conventional methods (including SM, MM and DGMM). In order to avoid any bias caused by random data division, 10 times independent non-repetitive 5-fold cross-validation is implemented to further evaluate the average regression performance. The average results of RMSE and CC among the 5-fold training and testing data on node and edge modalities are calculated respectively as shown in Table 2. SM yields the RMSE values of 0.6917 (0.6837), 0.7142 (0.6950) and CC values of 0.1787 (0.2028), 0.0068 (0.0785) on node and edge test (training) set, respectively. These results indicate that the functional connectivity edge information between brain regions contains useful information for mechanistic understanding of AD. In addition, MM produces the RMSE values of 0.5602 (0.4528), 0.6635 (0.5856) and CC values of 0.5696 (0.7410), 0.2380 (0.5057) on node features and edge features test (training) set, respectively, which are better than those of SM. These results indicate that the MM method can jointly select the node and edge features. Moreover, DAMM exports the best RMSE values of 0.5498 (0.4648), 0.6577 (0.5869) and the best CC values of 0.5854 (0.7571), 0.2446 (0.5227) on node and edge features test (training) set, respectively, which indicate the advantages of using the diagnosis-aligned regularization term. Meanwhile, we have made pairwise t-test based on the results of 5-fold cross-validation and added the P-values in Table 2. The resulting P-value (P < 0.05) shows that the improvement for our method is statistically significant.
Table 2.
Comparison of regression performance of node features and edge features by different methods
| Method | RMSE (mean ± SD) |
P-value | CC (mean ± SD) |
P-value | |||
|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | ||||
| SM | Node | 0.6837 ± 0.0101 | 0.6917 ± 0.0201 | < 1e-3 | 0.2028 ± 0.0261 | 0.1787 ± 0.1050 | <1e-3 |
| Edge | 0.6950 ± 0.0061 | 0.7142 ± 0.0554 | <1e-3 | 0.0785 ± 0.0201 | 0.0068 ± 0.1120 | <1e-3 | |
| MM | Node | 0.4528 ± 0.0098 | 0.5602 ± 0.0285 | <1e-3 | 0.7410 ± 0.0239 | 0.5696 ± 0.1016 | <1e-3 |
| Edge | 0.5856 ± 0.0066 | 0.6635 ± 0.0254 | <1e-3 | 0.5057 ± 0.0191 | 0.2380 ± 0.1170 | <1e-3 | |
| DGMM | Node | 0.4572 ± 0.0032 | 0.5526 ± 0.0032 | 0.0426 | 0.7439 ± 0.0012 | 0.5799 ± 0.0043 | 0.0396 |
| Edge | 0.5891 ± 0.0024 | 0.6621 ± 0.0015 | <1e-3 | 0.5131 ± 0.0026 | 0.2333 ± 0.0044 | <1e-3 | |
| DAMM | Node | 0.4648 ± 0.0132 | 0.5498 ± 0.0033 | – | 0.7571 ± 0.0077 | 0.5854 ± 0.0087 | – |
| Edge | 0.5869 ± 0.0029 | 0.6577 ± 0.0019 | – | 0.5227 ± 0.0070 | 0.2446 ± 0.0013 | – | |
Note: The best results are highlighted in bold.
In our method, there are two regularization items, i.e. the sparsity regularizer λ1 and diagnosis-aligned regularization term . The two parameters control the relative contribution of those regularization terms. Here, the values of λ1 and λ2 are respectively set in the range of to observe the effect of the diagnosis-aligned regularization term on the regression performance of our proposed method. Figure 4 shows the results when λ1 ( in this article) is fixed, the results are with respect to different values of λ2. When , no diagnosis-aligned regularization item is introduced, and thus our proposed method will degenerate into the MM method. As shown in Figure 4, with all values of λ2, our proposed algorithm consistently outperforms the MM method, which further indicates the advantages of the diagnosis-aligned regularization term.
Fig. 4.
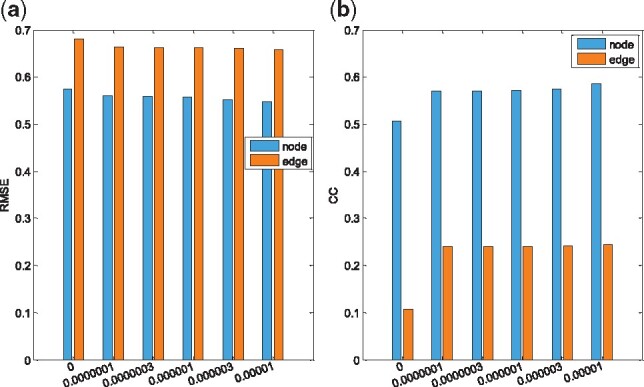
The regression performance with the regularization parameter λ2. (a) RMSE, (b) CC. X-axis represents different values for λ2
3.4 Identification of the most related node ROI marker
Besides the improved performances, one major goal of this study is to identify some significant and related phenotypes that are highly correlated to both risk SNP markers and disease status to capture imaging genetics associations in AD research.
For the node features, we average the obtained sparse coefficients by 5-fold cross-validation. Then, the top 10 maximum weight ROIs are selected as the important ROI marker. The top 10 selected MRI-VBM imaging features as shown in Table 3, as well as their average regression coefficients across five cross-validation trials, are visualized in Figure 5 by mapping them onto the human brain. The colors of the selected brain regions indicate the regression coefficients of the corresponding MRI-VBM markers. It should be noted that these selected ROIs most are in accordance with the previous studies. Structural imaging studies have already identified several diagnostic markers of AD: hippocampus, amygdala and parahippocampal gyrus (de Leon et al., 1995; Echávarri et al., 2011; Horínek et al., 2007). The literature (de Jong et al., 2008) shows that the volume of the pallidum and putamen is significantly correlating to the volume of the neocortical gray matter in subjects. However, there are different degrees of brain gray matter atrophy in AD subjects (Karas et al., 2004). The structural characteristics of right sup-motor-area and right precentral gyrus are closely related to the onset of AD (Iwai et al., 1995; Jenkins et al., 1992), and a large number of clinical examples have proved that there are certain obstacles in the movement and perception of advanced Alzheimer’s patients in this areas. For example, patients often have the abnormal symptoms of stiff hands and feet, curl and incontinence. In Foundas et al. (1997), the paper shows that the insula may be involved early in AD and that atrophy of the insular cortex may contribute to the cognitive deficits typical of early AD. And the left inferior frontal gyrus (opercular) has potentially associated with MCI (Shen et al., 2010).
Table 3.
The top 10 ROIs selected by the node features
| ID | Name |
|---|---|
| 39 | R. Parahippocampal gyrus |
| 37 | L. Hippocampus |
| 2 | R. Precentral gyrus |
| 73 | L. Putamen |
| 20 | R. Supplementary motor area |
| 75 | L. Pallidum |
| 30 | R. Insula |
| 40 | L. Parahippocampal gyrus |
| 11 | L. Inferior frontal gyrus (opercular) |
| 42 | R. Amygdala |
Note: L, left; R, right
Fig. 5.
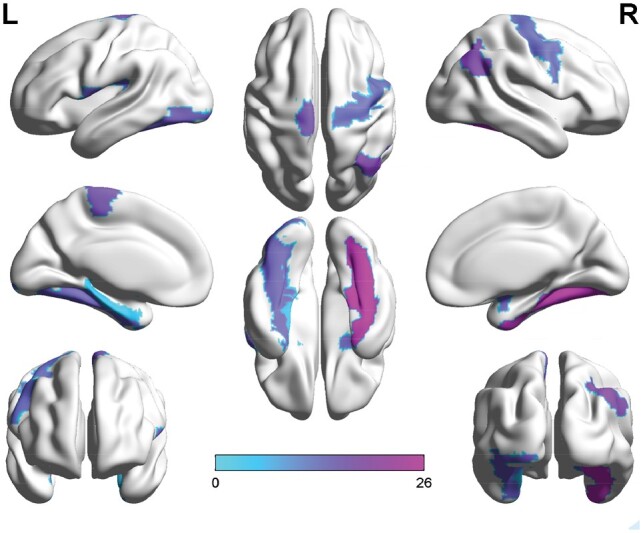
Visualization of the mapping top 10 ROIs selected by the node features. The color represents the regression coefficients of the corresponding VBM markers (Color version of this figure is available at Bioinformatics online.)
3.5 Identification of the most related edge ROI marker
The brain network model is a simple representation of the brain system. The nodes are defined as brain regions. And the edges correspond to connections between brain regions. In our article, we construct the brain connectivity hyper-networks, and the clustering coefficients are defined as edge features. After extracting a set of clustering coefficients from the brain connectivity hyper-networks, the clustering coefficients are absorbed into each brain region, i.e. the obtained feature dimension is the same as the brain region dimension, and each dimension corresponds to a brain region. We can get the ROI imaging features by the proposed method.
For the edge features, we also average the obtained sparse coefficients by 5-fold cross-validation and select the top 10 maximum weight ROIs as the important ROI marker. Table 4 presents the top 10 ROI imaging features, which illustrates that the selected ROIs such as left precuneus and right superior occipital gyrus are related to the structure atrophy, pathological amyloid depositions and metabolic alteration in the brain (Camus et al., 2012; Karas et al., 2007; Liu et al., 2015; Reiman et al., 1996; Wishart et al., 2006), showing effectiveness of the proposed method. The reduction of the putamen gray matter has been correlated with APOE SNP rs429358 (de Jong et al., 2008; Karas et al., 2004). In Jacobs et al. (2012) and Shen et al. (2010), the papers show that the right superior parietal gyrus and right inferior frontal gyrus (opercular) areas are most commonly associated with MCI. Besides confirming the prior findings, our method also yields the associations between APOE rs429538 and other eminent AD markers such as left orbitofrontal cortex (middle) and right superior frontal gyrus (media), left cuneus, right fusiform gyrus and left postcentral gyrus. There also appear to be specific relationships among genotypes, phenotypes and neuropsychiatric symptoms that deserve further investigation.
Table 4.
The top 10 ROIs selected by the edge features
| ID | Name |
|---|---|
| 50 | R. Superior occipital gyrus |
| 67 | L. Precuneus |
| 57 | L. Postcentral gyrus |
| 56 | R. Fusiform gyrus |
| 12 | R. Inferior frontal gyrus (opercular) |
| 24 | R. Superior frontal gyrus (media) |
| 60 | R. Superior parietal gyrus |
| 74 | R. Putamen |
| 46 | R. Cuneus |
| 9 | L. Orbitofrontal cortex (middle) |
Note: L, left; R, right
Otherwise, to analyze the connectivity of selected brain regions and to graphically show differences on connectivity hyper-network between AD patients and NC, we compute the average hyper-edges based on the selected maximum weight ROI (right superior occipital gyrus) and the smaller weight ROI (right cuneus) in Table 4 for each group (i.e. AD and NC). Specifically, for the maximum weight ROI and the smaller weight ROI listed in Table 4, the following steps are repeated to construct hyper-edges of NC and AD groups. First, for each subject in each group, we first construct a hyper-edge using (4), and calculate the edges of the highest occurrence frequency. Finally, for each group, the top 8 ROIs with the highest occurrence number are selected to construct the corresponding average hyper-edges. Figure 6 graphically shows the average hyper-edges constructed on the maximum weight ROI and the smaller weight ROI [BrainNet is used to plot the hyper-edges (http://www.nitrc.org/projects/bnv/) (Xia et al., 2013)]. As seen in Figure 6, the hyper-edges of the selected maximum weight ROI in the AD group are obviously different from those in the NC group. However, the hyper-edges of the selected smaller weight ROI in the AD group are the same as those in the NC group. These results confirm that the identified significant brain ROI (the selected maximum weight ROI) is indeed related to AD.
Fig. 6.
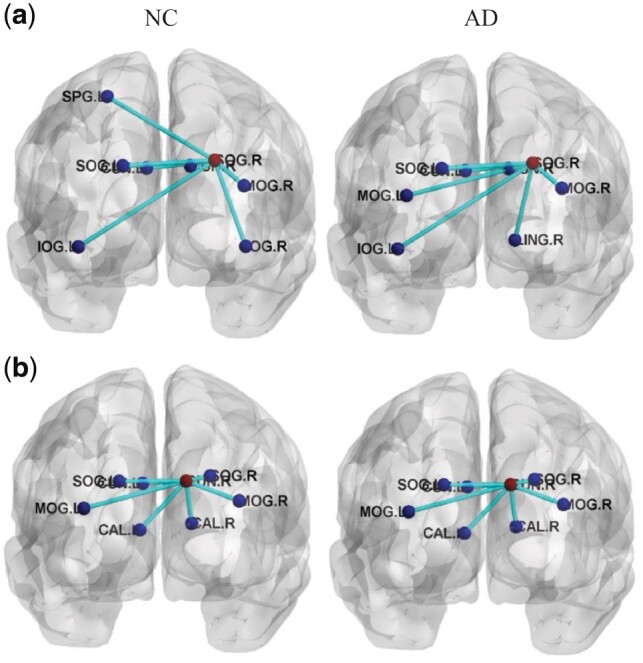
The average hyper-edges for NC (left) and AD (right) groups based on the maximum weight ROI and the smaller weight ROI listed in Table 4. Here, each sub-figure denotes a hyper-edge constructed based on the corresponding ROI, where all nodes in each sub-figure form a hyper-edge, the red node (i.e. centroid node linked by other nodes) in each sub-figure represents the ROI used for constructing the hyper-edge, and the blue nodes represent the corresponding ROIs. (a) R. Superior occipital gyrus (SOG.R) [L. Inferior occipital gyrus (IOG.L), L. Middle occipital gyrus (MOG.L), L.Supperior occipital gyrus (SOG.L), L.Cuneus (CUN.L), R. Lingual gyrus (LING.R), R. Cuneus (CUN.R), R. Middle occipital gyrus (MOG.R), L. Superior parietal gyrus (SPG.L), R. Inferior occipital gyrus (IOG.R)]; (b) R. Cuneus (CUN.R) [L. Middle occipitial gyrus (MOG.L), L. Superior occipitial gyrus (SOG.L), L.Cuneus (CUN.L), L. Calcarine cortex (CAL.L), R. Calcarine cortex (CAL.R), R. Superior occipital gyrus (SOG.R), R. Middle occipital gyrus (MOG.R)] (Color version of this figure is available at Bioinformatics online.)
By the above analysis, it is further demonstrated that the functional connectivity information between brain regions could help mine the significant brain ROIs associated with the top risk genotype.
3.6 Identification of the most stable ROI marker
We average the obtained sparse coefficients by our proposed DAMM method. The overall average regression coefficients which are combinations of brain network features phenotype for the ROIs are plotted in Figure 7. The association weight map shows that the selected imaging markers by our proposed method have clear patterns that span across all the average five cross-validation trials. The different metric features, node features and edge features, have identified some related ROI markers. And these identified phenotypic markers are from extremely stable ROIs such as left hippocampus, right parahippocampal gyrus and putamen. The identified stable markers strongly agree with the existing findings, which further demonstrated that connectivity features can be used as the complementary information to identify phenotypic markers.
Fig. 7.
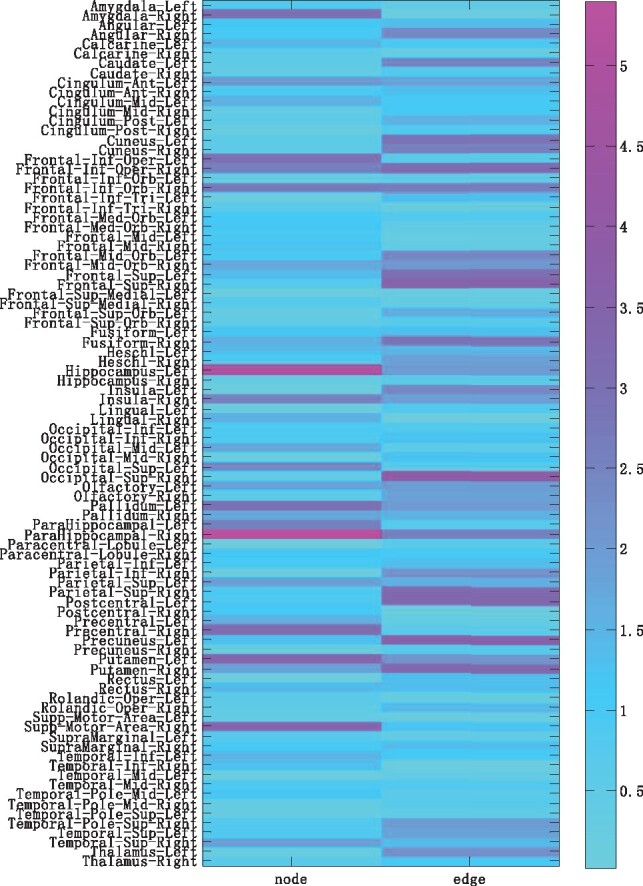
Weight maps on the associations between network phenotype and APOE rs429358 across average five cross-validation trials by proposed methods
4 Limitation
There are several limitations that should be further discussed in the current study. First, we associate only the small samples, while our proposed method considers the relationship between subjects to further improve the performance for the association analysis, and the small samples limit the heritability relationship. Therefore, much more samples should be used in our experiments in future. Second, the correlation coefficients (i.e. the correlation coefficients from the edge features) are low in the experimental results, which only demonstrate that the functional connectivity information between brain regions could help mine the significant brain ROIs associated with the top risk genotype. However, there also appear to be specific relationships among genotypes and connectivity phenotypes that deserve further investigation. Finally, we only investigate the top risk SNP (i.e. APOE rs429358) association with the AD problem, and do not test the risk SNP association with MCI problem, which is important to diagnose different stages of dementia.
5 Conclusion
In this article, a brain imaging genetics study has been performed to explore the relationship between two brain network features and the well-known AD risk SNP APOE rs429358. Because most of the current studies only focus on the associations between brain structure imaging and genetic variants, while neglecting the functional connectivity information between brain regions. A novel framework has been proposed to use structural voxel information and network connectivity information as intermediate traits that bridge genetic risk factors and disease status. In addition, most of existing multi-modality methods are designed to select more discriminative features by embedding complementary information between multimodal data, which only consider relationship between modalities of the same subjects, and neglect the possible internal relations among modalities of the different subjects. A diagnosis-aligned multi-modality method has been adopted to fully explore the relationships among modalities of the different subjects. The promising empirical results demonstrated that our method significantly outperforms the traditional methods. Furthermore, the diagnosis-aligned multi-modality method could effectively mine the possible internal relations among modalities of the different subjects, as well as yield improved performances and biologically meaningful findings from real data. This study is an initial attempt to explore the relation between the connectivity features and genetic variants.
The future research topics are to further investigate how to construct the brain network model and mine more brain network features for exploring some biologically meaningful results.
Acknowledgements
Data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Bio-gen; Bristol-Myers Squibb Company; CereSpir, Inc.; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Disease Cooperative Study at the University of California, San Diego. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California.
Contributor Information
Meiling Wang, Department of Computer Science and Technology, College of Computer Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing, China.
Xiaoke Hao, Department of Internet of Things Engineering, School of Artificial Intelligence, Hebei University of Technology, Tianjin, China.
Jiashuang Huang, Department of Computer Science and Technology, College of Computer Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing, China.
Wei Shao, Department of Computer Science and Technology, College of Computer Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing, China.
Daoqiang Zhang, Department of Computer Science and Technology, College of Computer Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing, China.
Funding
This work was supported by the National Natural Science Foundation of China (nos. 61422204, 61473149, 61732006, 61876082 and 61806071).
Conflict of Interest: none declared.
References
- Brookmeyer R., et al. (2007) Forecasting the global burden of Alzheimer’s disease. Alzheimers Dement., 3, 186–191. [DOI] [PubMed] [Google Scholar]
- Camus V., et al. (2012) Using PET with 18F-AV-45 (florbetapir) to quantify brain amyloid load in a clinical environment. Eur. J. Nucl. Med. Mol. Imaging, 39, 621–631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X., et al. (2009) Accelerated Gradient Method for Multi-Task Sparse Learning Problem. ICDM, Florida, pp. 746–751. [Google Scholar]
- de Jong L.W., et al. (2008) Strongly reduced volumes of putamen and thalamus in Alzheimer’s disease: an MRI study. Brain, 131, 3277–3285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Leon M.J., et al. (1995) The hippocampus in aging and Alzheimer’s disease. Neuroimag. Clin. N. Am., 5, 1–17. [PubMed] [Google Scholar]
- Du L., et al. (2016) Structured sparse canonical correlation analysis for brain imaging genetics: an improved graphnet method. Bioinformatics, 32, 1544–1551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Echávarri C., et al. (2011) Atrophy in the parahippocampal gyrus as an early biomarker of Alzheimer’s disease. Brain Struct. Funct, 215, 265–271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foundas A.L., et al. (1997) Atrophy of the hippocampus, parietal cortex, and insula in Alzheimer’s disease: a volumetric magnetic resonance imaging study. Neuropsychiatry Neuropsychol. Behav. Neurol., 10, 81–89. [PubMed] [Google Scholar]
- Fu Y., et al. (2015) Genetic influences on resting-state functional networks: a twin study. Hum. Brain Mapp., 36, 3959–3972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallagher S.R., Goldberg D.S. (2013) Clustering Coefficients in Protein Interaction Hypernetworks. BCB, Washington, DC, pp. 552–560. [Google Scholar]
- Ge T., et al. (2013) Imaging genetics-towards discovery neuroscience. Quantitat. Biol., 1, 227–245. [Google Scholar]
- Glahn D.C., et al. (2007) Neuroimaging endophenotypes: strategies for finding genes influencing brain structure and function. Hum. Brain Mapp., 28, 488–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hao X., et al. (2016) Identifying multimodal intermediate phenotypes between genetic risk factors and disease status in Alzheimer’s disease. Neuroinformatics, 14, 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horínek D., et al. (2007) Magnetic resonance analysis of amygdalar volume in Alzheimer’s disease. Curr. Opin. Psychiatry, 20, 273–277. [DOI] [PubMed] [Google Scholar]
- Iwai A., et al. (1995) The precursor protein of non- component of Alzheimer’s disease amyloid is a presynaptic protein of the central nervous system. Neuron, 14, 467–475. [DOI] [PubMed] [Google Scholar]
- Jacobs H.I.L., et al. (2012) Parietal cortex matters in Alzheimer’s disease: an overview of structural, functional and metabolic findings. Neurosci. Biobehav. Rev., 36, 297–309. [DOI] [PubMed] [Google Scholar]
- Jenkins I.H., et al. (1992) Impaired activation of the supplementary motor area in Parkinson’s disease is reversed when akinesia is treated with apomorphine. Ann. Neurol., 32, 749–757. [DOI] [PubMed] [Google Scholar]
- Jie B., et al. (2014) Brain Connectivity Hyper-Network for MCI Classification. MICCAI, Boston, MA, pp. 724–732. [DOI] [PubMed] [Google Scholar]
- Jie B., et al. (2014) Topological graph kernel on multiple thresholded functional connectivity networks for mild cognitive impairment classification. Hum. Brain Mapp., 35, 2876–2897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jie B., et al. (2015) Manifold regularized multitask feature learning for multimodality disease classification. Hum. Brain Mapp., 36, 489–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jie B., et al. (2016) Hyper-connectivity of functional networks for brain disease diagnosis. Med. Image Anal., 32, 84–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karas G., et al. (2007) Precuneus atrophy in early-onset Alzheimer’s disease: a morphometric structural MRI study. Neuroradiology, 49, 967–976. [DOI] [PubMed] [Google Scholar]
- Karas G.B., et al. (2004) Global and local gray matter loss in mild cognitive impairment and Alzheimer’s disease. Neuroimage, 23, 708–716. [DOI] [PubMed] [Google Scholar]
- Liu Y., et al. (2015) APOE genotype and neuroimaging markers of Alzheimer’s disease: systematic review and meta-analysis. J. Neurol. Neurosurg. Psychiatry, 86, 127–134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reiman E.M., et al. (1996) Preclinical evidence of Alzheimer’s disease in persons homozygous for the epsilon 4 allele for apolipoprotein E. N. Engl. J. Med., 334, 752–758. [DOI] [PubMed] [Google Scholar]
- Shao W., et al. (2018) Ordinal Multi-Modal Feature Selection for Survival Analysis of Early-Stage Renal Cancer. MICCAI, Granada, Spain, pp. 648–656. [Google Scholar]
- Shen L., et al. (2010) Whole genome association study of brain-wide imaging phenotypes for identifying quantitative trait loci in MCI and AD: a study of the ADNI cohort. Neuroimage, 53, 1051–1063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song A., et al. (2016) Network-based analysis of genetic variants associated with hippocampal volume in Alzheimer’s disease: a study of ADNI cohorts. BioData Mining, 9, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O. (2014) Contributions and challenges for network models in cognitive neuroscience. Nat. Neurosci., 17, 652–660. [DOI] [PubMed] [Google Scholar]
- The Genomes Project Consortium. (2015) A global reference for human genetic variation, the 1000 genomes project consortium. Nature, 526, 68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R. (2011) Regression shrinkage and selection via the lasso: a retrospective, J . Roy. Statist. Soc., 73, 267–288. [Google Scholar]
- Winkler A.M., et al. (2010) Cortical thickness or grey matter volume? The importance of selecting the phenotype for imaging genetics studies. Neuroimage, 53, 1135–1146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wishart H.A., et al. (2006) Regional brain atrophy in cognitively intact adults with a single APOE epsilon4 allele. Neurology, 67, 1221–1224. [DOI] [PubMed] [Google Scholar]
- Xia M., et al. (2013) BrainNet viewer: a network visualization tool for human brain connectomics. PLoS One, 8, e68910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan J., et al. (2014) Transcriptome-guided amyloid imaging genetic analysis via a novel structured sparse learning algorithm. Bioinformatics, 30, 564–571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou D., Huang J. (2006) Learning with Hypergraphs: Clustering, Classification, and Embedding. NIPS, Vancouver, BC, Canada, pp. 1601–1608. [Google Scholar]
- Zhu H., et al. (2018) A novel method to test associations between a weighted combination of phenotypes and genetic variants. PLoS One, 13, e0190788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zille P., et al. (2017) Enforcing co-expression within a brain-imaging genomics regression framework. IEEE Trans. Med. Imaging. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zu C., et al. (2016) Label-aligned multi-task feature learning for multimodal classification of Alzheimer’s disease and mild cognitive impairment. Brain Imaging Behav., 10, 1148–1159. [DOI] [PMC free article] [PubMed] [Google Scholar]