Estimation of Tumor Volume with Fuzzy-Connectedness Segmentation of MR Images

Abstract

BACKGROUND AND PURPOSE: Reproducible measurements of brain tumor volume are helpful in evaluating the response to therapy and the need for changing treatment plans. Our purpose was to adapt the fuzzy-connectedness segmentation technique to measure tumor volume. This technique requires only limited operator interaction.

METHODS: Routine postoperative brain MR imaging was performed in 19 patients with primary malignant gliomas of the brain. Segmentation was performed on axial and coronal gadolinium-enhanced and axial fluid-attenuated inversion recovery (FLAIR) images by using a fuzzy-connectedness algorithm, and tumor volumes were generated. Operator interaction was limited to selecting representative seed points within the tumor and, if necessary, editing the segmented image to include or exclude improperly classified regions.

RESULTS: Measurements of tumor volume were highly reproducible when they were obtained with no editing; intraobserver coefficients of variation were 0.15–0.37% and 0.29–0.38%, respectively, for enhanced images and FLAIR images. Editing consistently produced smaller volumes, at the cost of greater variability in volume measurements. Coefficients of variation for volumes with editing ranged from 0.2% to 1.3%.

CONCLUSIONS: Fuzzy-connected segmentation permits rapid, reliable, consistent and highly reproducible measurement of tumor volume from MR images with limited operator interaction.

MR imaging of the brain is often used to monitor tumor response to treatment, in conjunction with other imaging techniques such as MR spectroscopy and positron emission tomography. Objective, accurate, and reproducible methods of measuring tumor volume are of the utmost importance to the clinicians in assessing the response to treatment and in guiding appropriate therapy in serial studies. Large variations occur in the size of tumor, amount of tumor edema, and enhancement characteristics, as subjectively measured or qualitatively assessed in routine practice. These problems are compounded in lesions that are poorly marginated, diffusely infiltrating, or multiple. Residual or recurrent tumors are particularly challenging because of irregular borders, postoperative hemorrhage, isolated or discontinuous patches of tumor, and nodular rings and arcs of enhancement that do not readily lend themselves to subjective measurement or assessment with planimetry.

Methods based on visual inspection for the assessment of change in tumor size and the response to treatment regimens have large interobserver variability (1). The computational process of detecting and delineating objects in images, referred to as image segmentation, has been a fertile area for research in the past few decades. A method involving manual tracing of tumor boundaries has inter- and intraobserver agreement indices similar to those of semiautomated methods, but it is more time-consuming (2). Various promising computer-assisted techniques to measure tumor volume have been described in the literature (1, 3–9). Of these, the most popular approaches are based on applying clustering techniques to the features extracted from multiprotocol MR imaging. The k nearest-neighbor, fuzzy c-means and its variants, and region-growing techniques have been used to segment tumor regions (1–3, 6–9). When manual tracing by a knowledgeable operator is used as truth, overall agreements for the results of automatic methods range from 82% to 94% (7). For some of these methods, the time required for the computations on a Sun 4/470 workstation has been reported to vary from several hours to several tens of hours. Presumably, with modern computing platforms, this time can be reduced to several minutes or several tens of minutes (7). A computer-assisted system with demonstrated routine applicability in a clinical environment does not seem to exist.

A computer assisted three-dimensional (3D) image segmentation framework that is minimally interactive and based on fuzzy-connectedness theory and principles was developed at our institution (10). Images are, by nature, fuzzy, and object intensities manifest themselves on images with a gradation of values in a nonbinary fashion. This gradation comes from the material heterogeneity of the object and from blurring, noise, and background variations introduced by the imaging device. Despite this graded composition of object regions, humans usually do not have any difficulty in perceiving these regions as a gestalt, and the image elements in them seem to “hang” together to represent the object. The fuzzy-connectedness theory and algorithms attempt to capture this notion in a computational framework. The main idea behind this theory is that a strength of connectedness is considered to exist between any two voxels v1 and v2 on the image. This strength is determined by considering all possible connecting paths between v1 and v2 in the 3D space. A path is simply a sequence of nearby voxels starting from v1 and ending on v2. Each path has a strength of connectedness associated with it that is determined by examining successive pairs of voxels along the path. Each pair of nearby voxels has an affinity associated with it that is determined on the basis of how close the voxels are spatially and how similar they are in their image-intensity characteristics. Affinity describes how strongly the voxels hang together locally in the same object. The strength assigned to a path is the smallest affinity of pairwise elements along the path. The strength of connectedness between any two elements v1 and v2 is the strength of the strongest of all paths between v1 and v2. To compute a fuzzy-connected object, the strength of connectedness between all possible pairs of voxels in the image must be determined. The theory leads to elegant solutions to this problem that seems computationally impractical and makes the computation of fuzzy-connected objects on acquired images practical (10).

In the fuzzy-connected method, operator interaction is limited to the selection of representative points—that is, seeding the segmentation—within the object of interest. It was successfully applied in more than 1000 studies in the following applications: quantification of lesions and component tissues of the brain with MR imaging in multiple sclerosis (11), segmentation of vessels with MR angiography and artery-vein separation (12), quantification of subglandular tissue with mammography for the assessment of breast cancer risk (13), and 3D visualization of muscles with CT for craniomaxillofacial surgery planning (14). In these applications, the method was shown to be highly reliable, reproducible, and consistent for volume measurement. We adapted the same method with requisite changes, as described later, to objectively and reproducibly measure enhancing tumor volume and regions of abnormal signal intensity on fluid-attenuated inversion recovery (FLAIR) images obtained to represent tumor and edema.

Methods

MR imaging data of 19 patients with primary malignant gliomas of the brain were included in this study. The patients were aged 20–72 years. Twelve were men, and seven were women. All patients had previously undergone surgery, as well as chemotherapy, radiation therapy, or both. Cytoreductive surgery had been performed some time prior to imaging, not necessarily immediately prior to MR imaging. All studies were performed with a 1.5-T GE MR imaging system with a head coil. A neuroradiologist and an image-processing scientist, henceforth referred to as operators 1 (G.M.) and 2 (J.L.), respectively, independently conducted all analyses of the routine brain MR images. Gadolinium-enhanced (0.1 mmol/kg) images were designated as T1e. Images used for segmentation were acquired with the following parameters: axial T1-weighted images, 400–717/8.0/1(TR/TE/NEX); axial FLAIR images, 10,000/133–145/1; axial T1e images, 500–600/8–20/1; and coronal T1e images, 500–700/8–20/1. Images had a FOV of 22 cm, a matrix of 256 × 192, and 5 mm interleaving.

The following patient subsets were created: 1) T1e axial and coronal images were segmented in 10 studies without editing. 2) FLAIR images were segmented in 10 studies without editing. 3) A second set of axial T1e images was acquired after the initial T1e axial and coronal images in a subset of five patients to study the effect of delay on the measured volume. The repeat T1e axial acquisition was performed with the same imaging parameters as the initial T1e axial acquisition. 4) Five patients underwent repeat FLAIR imaging after their head position was changed between the first and second FLAIR acquisitions to evaluate whether this introduced subjectivity to the volume measurements. For each of these patients, one operator (the neuroradiologist) determined the volumes three times on the second set of FLAIR images to account for intraobserver variability. 5) In six patients, operator 1 manually edited the T1e axial and coronal images to achieve the best subjective tumor segmentation. All images were processed on a 300 MHz Pentium computer by using the 3DVIEWNIX software system (15). Processing consisted of the following two steps for each patient data set.

Step 1: MR Imaging Intensity Normalization

Interpatient and intrapatient scanner-dependent variations in the MR image intensity cause considerable difficulties in MR image segmentation and analysis. To mitigate this problem, an intensity standardization method (16, 17) was applied to the acquired image data. This method was used to map the input intensities into intensities on a standard scale, which we chose to be [0, 4095] so that the mapped intensities on images acquired with the same protocol in the same body region had the same tissue meaning independent of the scanner and the patient. The map was achieved by deforming the histogram of the volume image to match, as well as possible, a standard histogram for that protocol and body region. Previous work (16) has shown that, when performed properly, this transformation retains the relationship of the intensities in the input image and never merges distinct input intensities into a single intensity. All images acquired with each of the protocols mentioned earlier (T1 weighted, T1e, FLAIR) were independently transformed so that the images obtained with the same protocol had the same tissue-specific intensity meaning.

From this point on, the processing steps for the FLAIR images were different from those for the T1-weighted and T1e images. For further reference, we use the following notations: I_F indicates the standardized FLAIR volume image; I_T1, the standardized T1-weighted volume image; I_T1e1, the standardized T1e volume image for the first axial acquisition; I_T1e2, the standardized T1e volume image for the coronal acquisition; and I_T1e3, the standardized T1e volume image for the second axial acquisition.

Step 2: Segmentation of FLAIR Images

On one section of an I_F, an operator indicated a rectangular box large enough to completely enclose the tumor and edema volume to be segmented (Fig 1A). This was not an attempt to trace the borders of the lesion; it simply served to limit the 3D region in which the subsequent analyses were performed. The range of the sections on the I_F covering the tumor was also specified. In this fashion, a rectangular box was specified in 3D on the I_F. All subsequent operations were confined to the part of the volume image within this box. This restriction was not necessary for the method to work, but by limiting the region to be analyzed, processing time was considerably reduced. We realized that the region of high signal intensity on the FLAIR images included both tumor and edema and that these could not be shown to be distinguished on the FLAIR images. For the purposes of this study, we referred to the region of abnormal high signal intensity on the FLAIR images as the FLAIR volume.

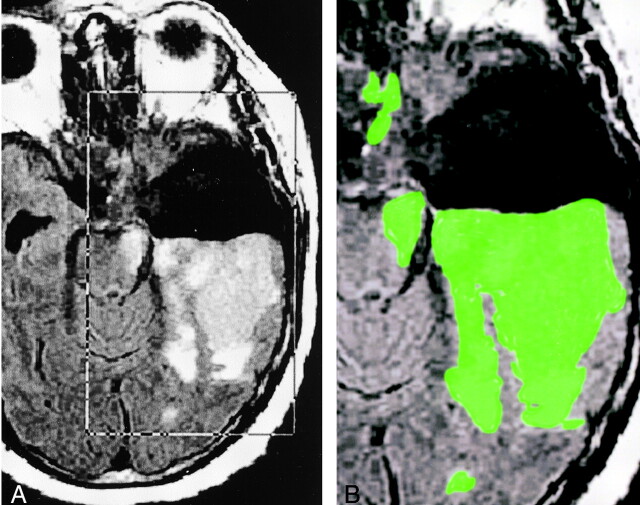
Fig 1.

Images illustrate step 2: segmentation of FLAIR images.

A, Placement of rectangular VOI around the area of presumed tumor and edema (FLAIR volume) on axial FLAIR images designated I_F.

B, Delineated FLAIR volume displayed as a green overlay obtained after the deposition of seed points in the VOI.

Next, seed points were specified within the tissue of interest. Although, typically, one point is sufficient, we specified several points, sprinkled in different sections so that even weakly connected parts of the tumor were detected. At this time, the tumor was automatically delineated in 3D as a fuzzily connected 3D object containing the specified points in a few seconds. The system then displayed the delineated tumor region as a colored overlay over the I_F in a section-by-section fashion for operator verification (Fig 1B). In the edited series, any extraneous segments (eg, scalp or orbital enhancement, which is occasionally detected if the tumor is close to these areas) were interactively deleted. False-negative regions rarely occurred. At the end of the process, the volume of the fuzzy-connected object was reported as the FLAIR volume. Step 2 was completed in approximately 2 minutes.

Step 3: Segmentation of Enhancing Tumor

To enable the distinction of hemorrhage from enhancing tumor, the I_T1e1 was first registered with the I_T1 by using an intensity correlation method (18, 19) that has been demonstrated to have an accuracy of as much as a voxel. The registered I_T1e1 was then redigitized by means of interpolation (15) to obtain sections that matched with those on the I_T1. This resulted in a new set of volume images, I′_T1e1. The difference image, I′_T1e1 − I_T1, was then computed (Fig 2). The procedure described in step 2 was repeated on this difference image to compute the enhancing tumor volume. The enhancing tissue included viable tumor, reactive inflammatory changes, and variable amounts of necrosis. We referred to the region of abnormal signal intensity as the enhancing volume.

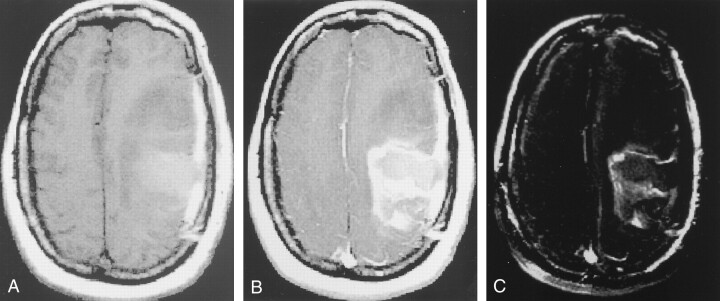
Fig 2.

Images illustrate step 3: segmentation of enhancing tumor.

A, I_T1, or T1-weighted axial image, demonstrates the postoperative cavity in the left frontoparietal area, with hemorrhage, edema, and possible residual tumor.

B, I_T1e1, or axial image obtained after the administration of gadolinium-based contrast material, shows rim enhancement along the margins of the postoperative cavity, as well as anterior nodular enhancement. Note the overlying postoperative dural enhancement.

C, I′_T1e1 − I_T1, or axial image obtained after subtracting the registered, resection volume in B from the volume in A, shows that only areas in which signal intensity increased on B compared with A have high signal intensity.

For segmentation in steps 2 and 3, the values of the parameters of the affinity relation for the fuzzy-connectedness algorithm were determined by using the training facility available in 3DVIEWNIX. Training was accomplished by painting the tumor and edema regions on one section in one patient study by using a paint brush attached to the mouse cursor. The required parametric values were then computed and fixed for all subsequent studies. To ensure that the standardized intensities on the T1 and T1e images were on the same scales (so that subtraction made sense), they were standardized by treating them within the same group as if they were obtained with the same protocol.

Subjectivity in our system for volume estimation was derived from the required operator interaction in segmentation and, possibly, from the way the patient was positioned in the imager.

The two operators—the neuroradiologist and the image-processing scientist—performed segmentation and measured tumor volumes. An initial learning process occurred; this involved selecting the number and position of the seed points within the tissue of interest. This tissue of interest was the area of enhancement on T1e images and the area of hyperintensity on the FLAIR images. From this initial experience, the operators obtained insight into the seeding process, learning which areas required more seeds (eg, areas that were weakly enhancing or nodular areas of enhancement separate from the main tumor mass). Operator interaction was limited to this seeding process and, in the edited series, to editing the segmented image to include or exclude improperly classified voxels. Each of the two operators obtained triplicate measures of the enhancing volume and FLAIR volume, without editing, on the subtracted T1e axial and on the coronal images to determine reproducibility and systematic differences that may have existed between the axial and coronal images. Similar measurements of edema plus the tumor volume were conducted by using the FLAIR images.

Inter- and intraobserver reproducibility were evaluated by using the coefficient of variation (defined as the standard deviation/mean) among the repeated measurements for each study. A paired t test was used to compare interobserver (for automated measurements) and intraobserver (for edited measurements) mean volumes and coefficients of variation.

Results

The total time required to generate all volumes in the above mentioned fashion was approximately 10 minutes per case (approximately 2 minutes for FLAIR images and approximately 3 minutes each for the T1e axial and coronal images). Nearly all the time required for these analyses represented operator interaction time. The computational processing itself was almost instantaneous.

In cases in which manual editing was performed on T1e axial and coronal images, the mean time required was approximately 7 minutes for each of the two acquisitions. The time required to generate volumes was dependent on the number of axial or coronal sections that included tumor. Only the neuroradiologist performed this editing, because it required knowledge of the enhancement pattern of residual and/or recurrent tumors. In cases in which non-neoplastic enhancing tissues (eg, dura, orbit, or scalp), were inadvertently included in the actual enhancing tumor segmentation, these were manually deleted by removing the portion of the image near these areas. This process did not require precise drawing of the tumor boundaries. When regions of enhancing tumor were not included in the segmentation by the fuzzy-connectedness process, they were included by means of manual tracing. This process was repeated for each study three times on different days.

Measurements of FLAIR and enhancing tumor volumes were highly reproducible when conducted with no editing, as well as with operator editing. The mean intraobserver coefficients of variation for FLAIR volumes were 0.27% and 0.21% for the two operators. For enhancing tumor volume, these values were 0.27% and 0.25% (Table 1). Interobserver concordance was excellent, with a coefficient of variation of 0.38% for FLAIR volumes and 0.33% for enhancing tumor (Table 1). Coefficients of variation for the two operators were comparable for enhancing tumor volume and FLAIR volume.

TABLE 1:

Percentage coefficient of variation for the estimated T1e and FLAIR volumes

Operator	T1e Mean (%)	T1e Axial (%)	T1e Coronal (%)	FLAIR (%)
1	0.27	0.37	0.15	0.27
2	0.25	0.27	0.23	0.21
Interobserver	0.33	0.29	0.37	0.38

Operator editing consistently produced smaller volumes (Table 2). The percentage coefficient of variation for manually edited T1e axial and coronal images was excellent, indicating high intraobserver reproducibility (Table 2).

TABLE 2:

Changes in measured tumor volume with editing

Image	Coefficient of Variation (%)
T1e axial automatic	1.0
T1e axial edited*	1.3
T1e coronal automatic	0.2
T1e coronal edited†	0.4

^*The median change with editing was −17.21%, with a range of −53.7% to 0.15%.

^†The median change with editing was −0.17%, with a range of −10.59% to 3.59%.

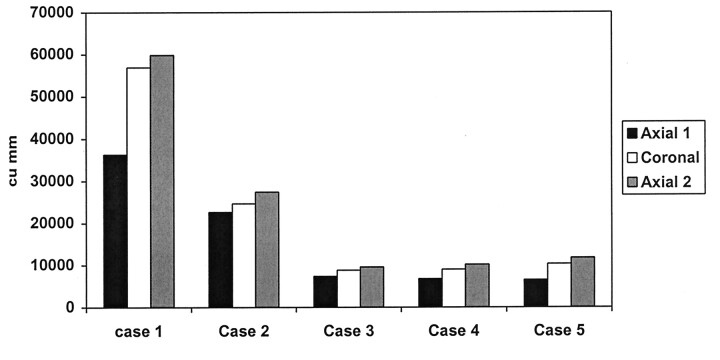
On initial data analysis, we found that enhancing tumor volumes on coronal images were generally larger than enhancing tumor volumes on axial images. We suspected that this finding was due to the time delay between the axial and coronal acquisitions: The axial acquisitions were always acquired earlier. The mean enhancing tumor volume measured on coronal T1e images was greater than that estimated from the axial T1e images (Fig 3). In the five cases in which an additional set of gadolinium-enhanced T1e axial images was obtained after the initial T1e axial and coronal acquisitions, the enhancing tumor volume obtained on the second set of axial T1e images was greater than that on the initial T1e axial volume by approximately 49%. Enhancing tumor volume on the second set of T1e axial images was, in turn, higher than the enhancing volume (by approximately 10.3%) on T1e coronal images, which were acquired earlier in the imaging sequence.

Fig 3.

Comparison of measured volumes from T1e initial axial, coronal, and repeat axial images.

FLAIR volumes measured on the second set of FLAIR images after a change in the head position were not significantly different from those measured from initial FLAIR images. This finding is important in serial imaging in patients who cannot be expected to be imaged in exactly the same position every time (Table 3).

TABLE 3:

Changes in unedited volumes with the first and second sets of FLAIR images

FLAIR Image Set	Coefficient of Variation (%)
First	0.64
Second*	0.59

^*The mean percentage volume change between the first and second sets was 2.53 cm.

For automated measures (on T1e axial, T1e coronal, and FLAIR images) interobserver differences in the mean volumes and coefficients of variation were not significant. We found no significant intraobserver difference between the edited and automated measures for T1e axial or T1e coronal measurements. Although no significant difference was observed in the tumor volume for the automated and edited measures, editing produced a more accurate measurement of tumor volume, because improperly classified pixels could be included or excluded.

Discussion

Neuroepithelial tumors account for 50–60% of primary intracranial tumors in adults. Glial neoplasms outnumber neuronal neoplasms by 100:1. Glioblastoma multiforme and anaplastic astrocytoma account for about 60% of glial neoplasms, and they are usually associated with a dismal prognosis (20–22). Earlier studies have demonstrated correlation between regions of contrast enhancement on MR Imaging and CT scans and areas of neovascularity and endothelial proliferation (23). These tumors are infiltrative and often extend beyond the enhancing tumor margin seen on MR Imaging and CT scan images (23–27). Despite this, the extent of tumor enhancement is used as an estimate of tumor volume, and it has prognostic importance (2, 28). Most protocols use information about enhancing tumor to determine the need for and the localization of radiation therapy after tumor resection. Stereotactic radiation therapy is targeted to the enhancing component of the tumor. The inclusion criteria for many chemotherapy protocols depend on the presence of residual enhancing tumor or the appearance or growth of such tumor at follow-up imaging. For these reasons, delineation of enhancing tissue is important for the evaluation of tumor status and for treatment planning.

Malignant gliomas almost always recur. The role of cytoreductive surgery in malignant gliomas is still controversial (29–30). At our institution, debulking surgery is performed in most cases of malignant gliomas. Although gross total resection is desirable, we do not withhold surgery in cases in which only partial removal of the gross tumor is possible. All patients undergo at least biopsy before further therapy is initiated, but, as in the cases included in this report, the surgeons always attempt to remove as much tumor as possible. A result of this approach is that a number of patients have residual enhancing tumor after cytoreductive surgery. Dewitte et al (29) reported a correlation between the amount of residual tumor and the likelihood of recurrence at 6 months. In some reports (20), the amount of residual tumor after extirpation of glioblastoma has been shown to have prognostic importance. Most malignant gliomas recur locally within 2 cm of the tumor margin (20, 22). Forsting et al (20) postulated that the local tumor recurrence in approximately 80% of their patients originated from macroscopic tumor rests, which were postoperatively seen as residual tumor. Twenty percent of their patients had a multicentric recurrence pattern, including components that were present away from the resection area. This was believed to reflect the migratory potential of malignant cells, with secondarily generalized neoplastic disease. Similar findings were reported in the studies of Hochberg and Pruitt (22), Donahue et al (31), and Sneed et al (32).

The measurement of tumor volume by means of image segmentation has been attempted in the past. A recent group (2) compared manual and semiautomatic methods for tumor volume measurement and found that semiautomated methods produced faster results with comparable inter- and intraoperator agreement.

Accurate and serially reproducible measurements of enhancing tumor volume have been a challenge in the field of imaging science in part because the usual pattern of tumor recurrence is nodular, irregular, discontinuous, and fuzzy. Vaidyanathan et al (3) reported an average intraobserver variation ranging from 5.8% to 8.9% for three semisupervised and unsupervised methods. The average interobserver variability ranged from 5.5% to 11.4% (3). In the study by Velthuizen et al (7), the average operator-dependent variation in tumor volume measurement ranged from 6% to 11%, with the manually traced volume used to represent truth. These authors suggested that minimally supervised or unsupervised methods might be preferable for tumor volume measurement because they have less operator dependence and improved reproducibility (6, 7).

The technique used in our study permitted rapid determination of reproducible tumor volumes, with limited operator interaction. The only source of variation for nonedited volumes was derived from the selection of initial seed voxels for the fuzzy-connected algorithm. By design, the position of the seed point was not critical. Provided that the seeds were placed somewhere in the volume of interest (VOI), this area was included in volume measurements. Seeding can change results only if one operator selects seed points that are outside the volume obtained by the second operator. Therefore, the two operators need not choose identical seed points, which is nearly impossible, but rather, only seed points which that are in the same included volume need to be selected. Likewise, in serial examinations, the same seed points need not be selected, rather, the seed points must be in the same volume of tissue as that on the prior image. This robustness property of fuzzy-connectedness segmentation to seed points has been mathematically proved in a prior paper (10). Nonetheless, variation in this seeding is likely to be responsible for most of the difference in interobserver and intraobserver variation for non-edited volumes, in which the former was slighter higher. The robustness property of fuzzy-connected delineation combined with MR imaging intensity standardization in step 1 (16, 17) is perhaps responsible for the low intra- and interobserver agreement and the repeat image variability with our method compared with those reported in the literature.

Note that our estimates of variation, reported here as coefficients of variation, include variability in measured volumes from all sources. Variation due to patient orientation in the machine was covered in repeat images studies in different head positions. In this study, the variability was caused almost entirely by variations in the selection of seed points and in the editing decisions. Variability due to the fuzzy-connectedness algorithm alone has been shown to be zero, provided that the seed points are within the same segmented region (10). Because this condition is often easy to achieve, application of the algorithm results in very low coefficients of variation.

Assessment of the accuracy of segmentation (33) is challenging in human studies, particularly with gliomas. No phantoms that approach the anatomic complexity of malignant gliomas are available. Thus, phantom studies are unlikely to reproduce the inherently fuzzy boundaries of real neoplasms. Tumors resected from animal models or humans also pose difficulties in the accurate quantification of the segmentation error. Determining the border of the tumor at surgery or histologic inspection may be just as difficult as it is with image segmentation. In fact, if histologic features are used as the criterion standard, one simply exchanges the segmentation problem on MR images for a segmentation problem on histologic images. These malignant gliomas do not have well-defined borders at histologic evaluation. Instead, they demonstrate a progressive decrease in the relative proportion of neoplastic versus non-neoplastic cells as one moves farther from the core of the lesion. The selection of a point that would be designated the tumor border would remain arbitrary. In these infiltrating tumors, the resected specimen almost never contains all of the tumor cells. Therefore, to use the resected volume as the criterion standard ensures underestimation of the true volume. Even a confirmation of similar volumes with a criterion standard, if such a standard existed, would not prove the accuracy of the segmentation because two objects can have identical volumes although their shapes may differ considerably. Therefore, to assess segmentation accuracy, we would need to estimate the following: 1) the part of the true volume that is missed with the segmentation algorithm (referred to as the false-negative volume fraction)m as well as 2) the part of the non-neoplastic tissue that is falsely included (referred to as the false-positive volume fraction). To estimate these entities (33), one would have to establish a point-to-point correspondence between the resected tumor and the image. For the reasons cited earlier, this sort of analysis is nearly impossible in human or animal studies.

The mean enhancing tumor volume measured on T1e coronal images was higher than that estimated from axial T1e images. This difference was likely due to the delay between the axial and coronal acquisitions. Several studies (34–39) of the time dependency of tumor enhancement with gadolinium-based contrast material have demonstrated peak enhancement at approximately 20–40 minutes. This result was confirmed in the five cases in which an additional set of gadolinium-enhanced T1e axial images was obtained after the initial T1e axial and coronal sets. In these cases, the enhancing tumor volume obtained on the second set of axial T1e images was greater than the initial T1e axial volume by approximately 49%. Enhancing tumor volume on the second set of T1e axial images was, in turn, higher than the enhancing volume (by approximately 10.3%) on T1e coronal images, which were acquired earlier in the imaging sequence. Our results are consistent with this well-established time-dependent pattern of gadolinium enhancement.

In cases in which intrinsically bright objects were close to the tumor (eg, enhancing vessels in the orbit, dura, or scalp), these were sometimes inadvertently included in the enhancing tumor volume segmented. This inclusion may have been due to the increased sensitivity of the subtracted images to even a minor degree of enhancement. These enhancing areas were perceived as enhancing tumor by the fuzzy-connectedness algorithm. They were manually excluded from the field of view by manipulating the size and shape of the box of interest prior to segmentation, or they were cut out by means of manual editing after segmentation, as described before. Editing requires knowledge of the appearance of recurrent tumors and must be conducted by neuroradiologists or experienced technologists. We demonstrated excellent reproducibility of the edited volumes. This resulted because editing involved deleting rather obvious areas of nontumor. In most cases, the true enhancing tumor volume was not changed. In some cases, the tumor volume generated on edited images was slightly higher. This difference was most likely occurred because the operator selected an inadequate number of seed points, especially at the edge of the enhancing tumor where the intensity of enhancement was low. We noted that the percentage coefficient of variation for the axial T1e images that were generated automatically (without editing) in this subgroup of cases (Table 2) was higher than that of the axial T1e images in the subgroup of patients that were not manual edited (Table 1). This difference may have been due to the smaller subset of images that underwent editing, increased variability in the placement of seed points by the operator, or the fact that the positioning of the seed points may have been more critical in this small subgroup of patients.

Changes in head positioning between the first and second FLAIR acquisitions in a patient subset did not produce significantly different volumes. Therefore, positioning should not be a problem in serial imaging and tumor quantification. This result, again, was perhaps due to the ability of the fuzzy-connected method to consistently handle the different degrees of partial volume effects that the tumor boundaries are subjected to in repeat imaging.

Although we did not implement this procedure in our system, segmenting the brain parenchyma in steps 2 and 3 before proceeding with the segmentation of enhancing tumor and edema is possible. We have used such an approach in the past (11) for delineating multiple sclerosis lesions in the brain. This approach would automatically exclude the extraneous objects, even before tumor segmentation starts. This exclusion can potentially further reduce operator interaction (and variability) in our system.

Conclusion

In conclusion, we have demonstrated that our method is reliable and consistent, with excellent intra- and interobserver agreement, repeat image reproducibility, and limited operator interaction. The analysis is rapid and easily learned. It may become part of the routine evaluation of patients with brain tumors in our hospital.