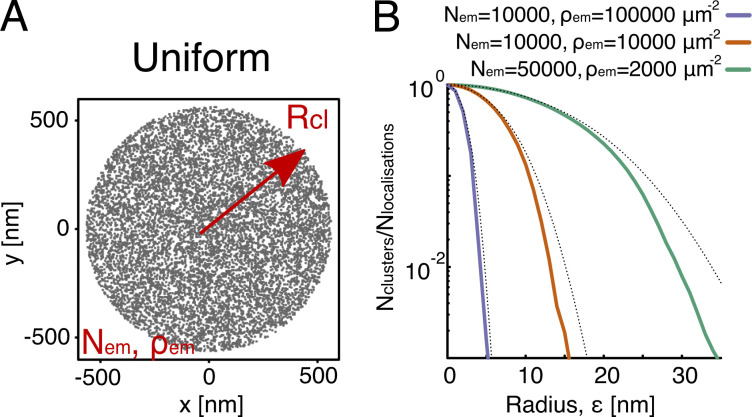
Figure S1.

The Poissonian functional form in the intra-cluster regime. (A) To test the Poissonian functional form (Eq. 1) of the intra-cluster regime of SuperStructure curves, we simulated localizations inside clusters as a uniform distribution of $N_{em}$ points distributed within a circle of radius $R_{cl}.$ The resulting average density is ${\rho }_{em}\mathrm{.}$ The number of points included in any circular subregion of radius $\epsilon$ is, on average, $n\left(\epsilon \right)=\pi {\rho }_{em}{\epsilon }^2,$ and is in fact itself Poisson distributed. (B) To check the theoretical prediction of Eq. 1, we have created simulated datasets for various ${\rho }_{em}$ and $N_{em}\mathrm{.}$ The theoretical predictions (dotted lines) with $m=2$ are in good agreement with the SuperStructure curves, indicating that indeed Eq. 1 correctly captures the behavior of uniformly distributed points forming one idealized cluster. However, note that for $m=2,$ there is already an overcounting of clusters at large values of $\epsilon$ due to the fact that DBSCAN merges indirectly related emitters in a single big cluster. This suggests not to extend the summation to higher values of $m\mathrm{.}$ From Eq. 1, the end of the intra-cluster regime can be approximated by the width of the Poisson function, i.e., ${\epsilon }^{*}\simeq 3{\kappa }_0$ (at 99% confidence level), where ${\kappa }_0=1/\sqrt{\pi {\rho }_{em}}$ is the decay length identified by Eq. 1. This is confirmed by observing that predicted ${\epsilon }^{*}$ for the curves are ${\epsilon }^{*}\left({\rho }_{em}=2\mathrm{,}000 \mu m^{-2}\right)\simeq 38 nm,$ ${\epsilon }^{*}\left({\rho }_{em}=10,000 \mu m^{-2}\right)\simeq 18 nm\mathrm{,}$ and ${\epsilon }^{*}\left({\rho }_{em}=100,000 \mu m^{-2}\right)\simeq 5.3 nm,$ which correspond to $N_{cl}/N_{em}\simeq {10}^{-3}$ (when most of the points have been merged in a single cluster).