Abstract
The aim of this research is to investigate the relationships between the counts of cases with Covid-19 and the deaths due to it in seven countries that are severely affected from this pandemic disease. First, the Pearson’s correlation is used to determine the relationships among these countries. Then, the factor analysis is applied to categorize these countries based on their relationships.
Keywords: Correlation, Factor analysis, Covid-19, Coronaviruses
Introduction
In the winter months of 2019–2020, another type of coronavirus, Covid-19, has been reported in Wuhan [1]. This virus has severe destructive effects on the respiratory system. From January to now (April 18, 2020), this epidemic has become epidemic all over the world and day by day the cases with Covid-19 and the deaths due to Covid-19 are extremely increasing in most of countries [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15]. There are many techniques analyze the natural phenomena including artificial intelligence, mathematical and statistical methods such as optimization, deep learning, time series analysis, machine learning, regression modeling, clustering and numerical analysis [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39]. Since Covid-19 has many impacts on environment, health, society and economy, the study of the rate of spread of this disease and the comparison of its rate in different countries is essential. There are some researches about the classification of Covid-19 datasets [40], [41], [42], [43]. These researches are based on time series analysis, principal component analysis and fuzzy clustering.
The aim of this research is to study the relationships between the counts of the cases with Covid-19 and the deaths due to it in seven countries that are severely affected from this pandemic disease. First, the coefficients of correlation are computed to determine the relationships between these countries. Then, the factor analysis is applied to categorize these countries using the counts of cases and deaths.
Material and method
This section is devoted to study the research’s dataset and to and to introduce the factor analysis.
Dataset
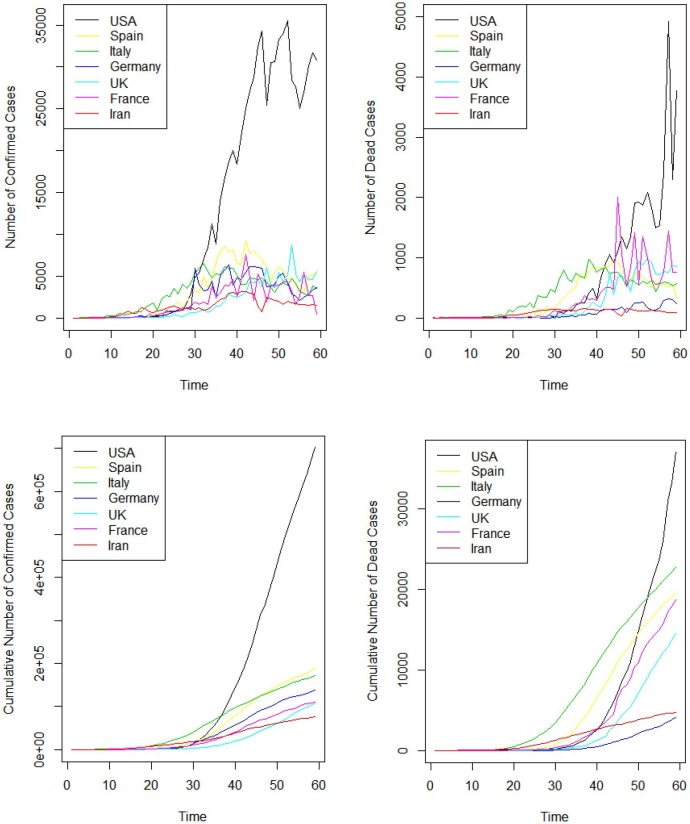
In this work, the counts of the cases with Covid-19 and the deaths due to it in United States America, United Kingdom, Spain, Italy, Iran, Germany, and France from February 22 to April 18 of 2020, are considered [43], [44]. Table 1 summarizes the descriptive statistics of dataset containing the mean and the standard deviation. It can be observed that Iran and United States America have the minimum and the maximum counts of the cases with Covid-19. In addition, Germany and United States America have the minimum and the maximum of the deaths due to Covid-19. The plots for the counts of the cases with Covid-19 and the deaths due to it are also demonstrated in Fig. 1 .
Table 1.
The mean and standard deviation for the counts of the cases with Covid-19 and the deaths due to this pandemic disease.
| Country | Mean ± Standard Deviation | |
|---|---|---|
| Cases | United States America | 11900.8 ± 13327.5 |
| Spain | 3187.6 ± 3016.8 | |
| Italy | 2922.6 ± 2056.1 | |
| Germany | 2329.2 ± 2245.2 | |
| France | 1851.5 ± 1876.0 | |
| United Kingdom | 1842.1 ± 2207.7 | |
| Iran | 1294.5 ± 921.5 | |
| Deaths | United States America | 628.0 ± 1013.4 |
| Italy | 385.5 ± 309.5 | |
| Spain | 330.1 ± 340.5 | |
| France | 316.6 ± 447.3 | |
| United Kingdom | 247.1 ± 342.0 | |
| Iran | 80.7 ± 55.6 | |
| Germany | 69.7 ± 94.9 | |
Fig. 1.
Counts of the cases (Left side of Top), counts of the deaths (Right side of Top), cumulative counts of the cases (Left side of Bottom), and cumulative counts of the deaths (Right side of Bottom).
The relationships between the rates of the spread of Covid-19 among these countries have been studied using Pearson’s coefficient of correlation. As it can be seen in Table 2 , all of the values are more than 0.5 and significant, and consequently there are strong positive relationships between the rates of spread of Covid-19 in all of countries.
Table 2.
Pearson’s coefficient of correlation between the rates of spread of Covid-19.
| United States America | Spain | Italy | Germany | United Kingdom | France | Iran | ||
|---|---|---|---|---|---|---|---|---|
| Patients | France | 1 | 0.586 | 0.850 | 0.766 | 0.851 | 0.856 | 0.673 |
| Germany | 0.586 | 1 | 0.654 | 0.514 | 0.562 | 0.550 | 0.942 | |
| Iran | 0.850 | 0.654 | 1 | 0.848 | 0.884 | 0.866 | 0.718 | |
| Italy | 0.766 | 0.514 | 0.848 | 1 | 0.842 | 0.879 | 0.567 | |
| Spain | 0.851 | 0.562 | 0.884 | 0.842 | 1 | 0.929 | 0.666 | |
| United Kingdom | 0.856 | 0.550 | 0.866 | 0.879 | 0.929 | 1 | 0.654 | |
| United States America | 0.673 | 0.942 | 0.718 | 0.567 | 0.666 | 0.654 | 1 | |
| Deaths | France | 1 | 0.802 | 0.621 | 0.677 | 0.815 | 0.804 | 0.716 |
| Germany | 0.802 | 1 | 0.565 | 0.629 | 0.764 | 0.927 | 0.885 | |
| Iran | 0.621 | 0.565 | 1 | 0.934 | 0.794 | 0.555 | 0.449 | |
| Italy | 0.677 | 0.629 | 0.934 | 1 | 0.892 | 0.626 | 0.508 | |
| Spain | 0.815 | 0.764 | 0.794 | 0.892 | 1 | 0.743 | 0.627 | |
| United Kingdom | 0.804 | 0.927 | 0.555 | 0.626 | 0.743 | 1 | 0.889 | |
| United States America | 0.716 | 0.885 | 0.449 | 0.508 | 0.627 | 0.889 | 1 | |
* p-value < 0.001.
Principles of factor analysis
Factor analysis (FA) as a popular multivariate statistical technique transforms some dependent features into some other features called factors such that the first factors of this transformation have the main information of the first dataset [45]. In other words, FA is used to convert a dataset with high dimensions to a dataset with lower dimensions, by considering minimum factors such that the dimension of the converted dataset is decreased. FA focuses on the correlations of variables such that the variables in a factor are highly correlated with each other and the variables in different factors are highly uncorrelated with each other. In applications, the number of the main factors in FA is usually considered as the number of the eigen-values of the correlation’s matrix with the values larger than one. To investigate the suitability of FA, the Kaiser-Meyer-Olkin (KMO) index is used. The KMO greater than 0.8 verifies the accuracy of FA.
Assume is a random vector. Denote
and
as the mean vector and covariance matrix of .
The equation of factor analysis with m factors () is presented by
such that
and
The matrix and the vectors and are called the factor loading matrix, the factors and errors, respectively.
This model can be rewritten by
such that is named as the loading of on the factor
In orthogonal factor analysis, we have
and
where
Consequently,
and
is determines the proportion of that can be explained by the factors , …,
The main aim of factor analysis is to find the values of the loadings. To compute the matrices and , different approaches such as principal component and maximum likelihood can be applied. Principal component approach uses eigen-values and eigen-vectors to decompose the matrix to find the matrix L. Maximum likelihood approach computes the likelihood and then optimize it to find the matrices and
When the loading values are estimated, we can consider loading plots. Loading plots can be used to
-
⁶
Study the correlations between variables
-
⁶
Categorize and Classify the variables
-
⁶
Detect the number of factors
In loading plot, the angle between two variables () determines the correlation () between them. = 90° verifies that two variables are uncorrelated (. The cases = 0° and = 180° refer to exact positive and negative linear relationship, respectively.
Results
This section reports the results of FA approach to classify the countries based on research’s variables. It should be noted that the number of the main factors in FA was considered as the number of the eigen-values of the correlation’s matrix with the values larger than one. Moreover, the KMO values were more than 0.8 that verify the accuracy of FA approach.
Counts of cases with Covid-19
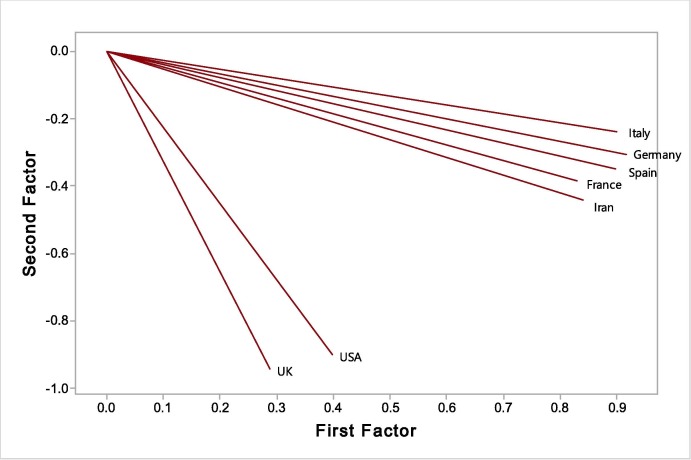
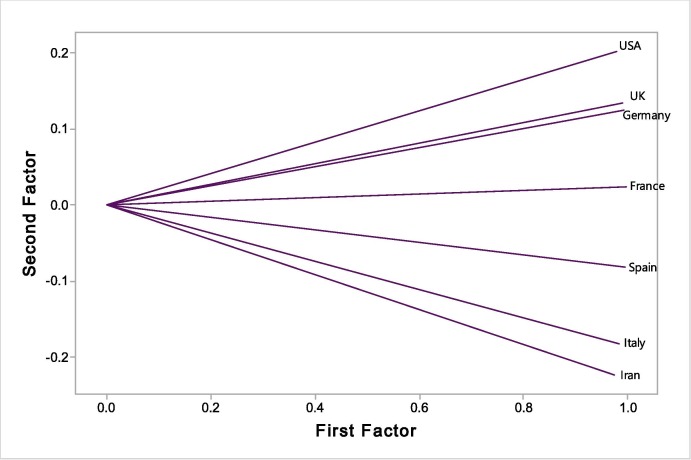
The results of FA technique to categorize the research countries, in basis of the counts of the cases with Covid-19, are provided in Fig. 2 . The outputs demonstrate the statistical differences between the relationships among the countries and we can categorize the countries into following classes:
Fig. 2.
FA technique to categorize the countries in basis of the counts of the cases with Covid-19.
First class: Iran, France, Spain, Germany, Italy.
Second class: United Kingdom, United States America.
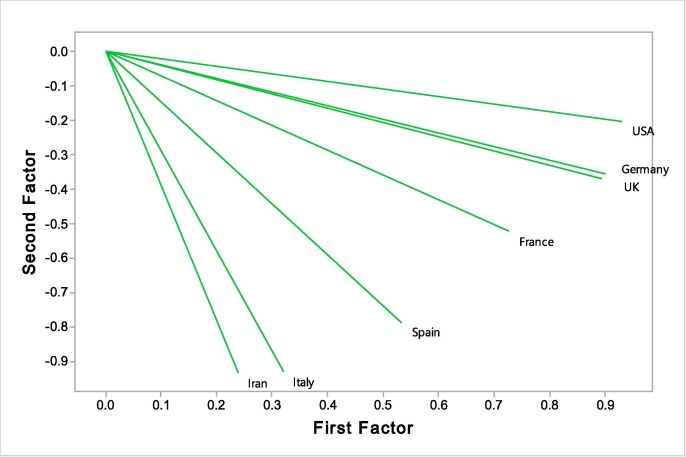
Counts of the deaths due to Covid-19
The results of FA technique to categorize the research countries, in basis of the counts of the deaths due to Covid-19, are provided in Fig. 3 . The outputs demonstrate the statistical differences between the relationships among the countries and we can categorize the countries into following classes:
Fig. 3.
FA technique to categorize the countries in basis of the counts of the deaths due to Covid-19.
First class: France, United Kingdom, Germany and United States America.
Second class: Iran, Italy and Spain.
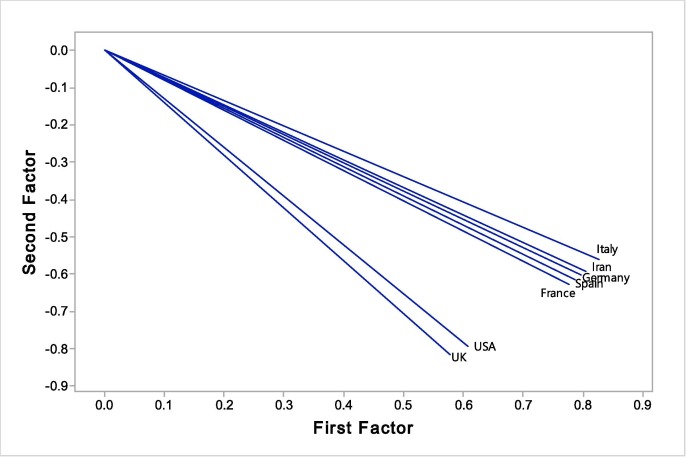
Cumulative counts of the cases with Covid-19
The results of FA technique to categorize the research countries, in basis of the cumulative counts of the cases with Covid-19, are provided in Fig. 4 . The outputs demonstrate the statistical differences between the relationships among the countries and we can categorize the countries into following classes:
Fig. 4.
FA technique to categorize the countries in basis of the cumulative counts of the cases with Covid-19.
First class: France, Spain, Germany, Iran and Italy.
Second class: United Kingdom and United States America.
Cumulative counts of the deaths due to Covid-19
The results of FA technique to categorize the research countries, in basis of the cumulative counts of the deaths due to Covid-19, are provided in Fig. 5 . The outputs demonstrate the statistical differences between the relationships among the countries and we can categorize the countries into following classes:
Fig. 5.
FA technique to categorize the countries in basis of the cumulative counts of the deaths due to Covid-19.
First class: France, United Kingdom, Germany and United States America.
Second class: Iran, Italy and Spain.
Conclusion
Since Covid-19 has many impacts on environment, health, society and economy, the study of the rate of spread of this disease and the comparison of its rate in different countries is essential. The aim of this research was to study the cases with Covid-19 and the deaths due to this pandemic disease in seven countries that are severely affected from this pandemic disease. The cases and the deaths in United States America, United Kingdom, Spain, Italy, Iran, Germany, and France from February 22 to April 18 of 2020, were considered. First, the coefficients of correlation were computed to determine the relationships among these countries. The outputs showed that there were strong positive relationships between the rates of spread in all of countries. Then, the factor analysis was applied to categorize the countries in basis of the counts and deaths. For the cases with Covid-19, United Kingdom and United States America were similarly distributed to each other and were differently distributed from other countries. Also, for the deaths, Iran, Italy and Spain were similarly distributed to each other and were differently distributed from other countries. For future works, the authors suggest classifying the Covid-19 datasets of more regions based on FA technique, or apply this technique to classify the regions for other epidemic or pandemic diseases.
CRediT authorship contribution statement
Mohammad Reza Mahmoudi: Conceptualization, Investigation, Data curation, Validation, Methodology, Software, Writing - original draft. Dumitru Baleanu: Conceptualization, Supervision, Visualization, Writing - review editing. Shahab S. Band: Validation, Visualization, Software, Writing - review editing. Amir Mosavi: Visualization, Writing - review editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Lu R., Zhao X., Li J., Niu P., Yang B., Wu H. Genomic characterisation and epidemiology of 2019 novel coronavirus: implications for virus origins and receptor binding. The Lancet. 2020;395(10224):565–574. doi: 10.1016/S0140-6736(20)30251-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Burke R.M., Midgley C.M., Dratch A. Active Monitoring of Persons Exposed to Patients with Confirmed COVID-19 — United States, January–February 2020. MMWR Morb Mortal Wkly Rep. 2020;69:245–246. doi: 10.15585/mmwr.mm6909e1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hunter D.J. Covid-19 and the stiff upper lip—the pandemic response in the united kingdom. N Engl J Med. 2020 doi: 10.1056/NEJMp2005755. [DOI] [PubMed] [Google Scholar]
- 4.Razai M.S., Doerholt K., Ladhani S., Oakeshott P. Coronavirus disease 2019 (covid-19): a guide for UK GPs. BMJ. 2020;6:368. doi: 10.1136/bmj.m800. [DOI] [PubMed] [Google Scholar]
- 5.Lillie P.J., Samson A., Li A., Adams K., Capstick R., Barlow G.D. Novel coronavirus disease (Covid-19): the first two patients in the UK with person to person transmission. J Infect. 2020 doi: 10.1016/j.jinf.2020.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Legido-Quigley H., Mateos-García J.T., Campos V.R., Gea-Sánchez M., Muntaner C., McKee M. The resilience of the Spanish health system against the COVID-19 pandemic. Lancet Public Health. 2020 doi: 10.1016/S2468-2667(20)30060-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lazzerini M., Putoto G. COVID-19 in Italy: momentous decisions and many uncertainties. Lancet Global Health. 2020 doi: 10.1016/S2214-109X(20)30110-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Onder G., Rezza G., Brusaferro S. Case-fatality rate and characteristics of patients dying in relation to COVID-19 in Italy. JAMA. 2020 doi: 10.1001/jama.2020.4683. [DOI] [PubMed] [Google Scholar]
- 9.Remuzzi A., Remuzzi G. COVID-19 and Italy: what next? Lancet. 2020 doi: 10.1016/S0140-6736(20)30627-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Takian A., Raoofi A., Kazempour-Ardebili S. COVID-19 battle during the toughest sanctions against Iran. Lancet (London, England) 2020;395(10229):1035. doi: 10.1016/S0140-6736(20)30668-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rothe C., Schunk M., Sothmann P., Bretzel G., Froeschl G., Wallrauch C. Transmission of 2019-nCoV infection from an asymptomatic contact in Germany. N Engl J Med. 2020;382(10):970–971. doi: 10.1056/NEJMc2001468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Amrane S., Tissot-Dupont H., Doudier B., Eldin C., Hocquart M., Mailhe M. A respiratory virus snapshot. Travel Med Infect Dis. 2020;2020 doi: 10.1016/j.tmaid.2020.101632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Stoecklin S.B., Rolland P., Silue Y., Mailles A., Campese C., Simondon A. First cases of coronavirus disease 2019 (COVID-19) in France: surveillance, investigations and control measures, January 2020. Eurosurveillance. 2020;25(6):2000094. doi: 10.2807/1560-7917.ES.2020.25.6.2000094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gautret P., Lagier J.C., Parola P., Meddeb L., Mailhe M., Doudier B. Hydroxychloroquine and azithromycin as a treatment of COVID-19: results of an open-label non-randomized clinical trial. Int J Antimicrob Agents. 2020;20 doi: 10.1016/j.ijantimicag.2020.105949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fanelli D., Piazza F. Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos, Solitons Fractals. 2020;134 doi: 10.1016/j.chaos.2020.109761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Haghbin H., Mahmoudi M.R., Shishebor Z. Large sample inference on the ratio of two independent binomial proportions. J Math Ext. 2011;5(1):87–95. [Google Scholar]
- 17.Mahmoudi M.R., Mahmoodi M. Inferrence on the ratio of correlations of two independent populations. J Math Ext. 2014;7(4):71–82. [Google Scholar]
- 18.Mahmoudi M.R., Mahmoodi M. Inferrence on the ratio of variances of two independent populations. J Math Ext. 2014;7(2):83–91. [Google Scholar]
- 19.Mahmoudi M.R., Nematollahi A.R., Soltani A.R. On the detection and estimation of the simple harmonizable processes. Iran J Sci Technol (Sciences) 2015;39(2):239–242. [Google Scholar]
- 20.Mahmoudi M.R., Mahmoudi M., Nahavandi E. Testing the difference between two independent regression models. Commun Stat Theory Methods. 2016;45(21):6284–6289. [Google Scholar]
- 21.Nematollahi A.R., Soltani A.R., Mahmoudi M.R. Periodically correlated modeling by means of the periodograms asymptotic distributions. Stat Pap. 2017;58(4):1267–1278. [Google Scholar]
- 22.Mahmoudi M.R., Maleki M. A new method to detect periodically correlated structure. Comput Stat. 2017;32(4):1569–1581. [Google Scholar]
- 23.Zarei A.R., Mahmoudi M.R. Evaluation of changes in RDIst index effected by different Potential Evapotranspiration calculation methods. Water Resour Manag. 2017;31(15):4981–4999. [Google Scholar]
- 24.Bahrami M., Amiri M.J., Mahmoudi M.R., Koochaki S. Modeling caffeine adsorption by multi-walled carbon nanotubes using multiple polynomial regression with interaction effects. J Water Health. 2017;15(4):526–535. doi: 10.2166/wh.2017.297. [DOI] [PubMed] [Google Scholar]
- 25.Mahmoudi M.R., Maleki M., Pak A. Testing the difference between two independent time series models. Iran J Sci Technol A (Sciences) 2017;41:665–669. [Google Scholar]
- 26.Mahmoudi M.R., Behboodian J., Maleki M. Inference on the ratio of means in two independent populations. J Stat Theory Appl. 2017;16(3):366–374. [Google Scholar]
- 27.Mahmoudi M.R., Heydari M.H., Avazzadeh Z. On the asymptotic distribution for the periodograms of almost periodically correlated (cyclostationary) processes. Digital Signal Process. 2018;81:186–197. [Google Scholar]
- 28.Mahmoudi M.R. On comparing two dependent linear and nonlinear regression models. J Test Eval. 2018;47(1):449–458. [Google Scholar]
- 29.Mahmoudi M.R., Maleki M., Pak A. Testing the equality of two independent regression models. Commun Stat Theory Methods. 2018;47(12):2919–2926. [Google Scholar]
- 30.Heydari M.H., Avazzadeh Z., Mahmoudi M.R. Chebyshev cardinal wavelets for nonlinear stochastic differential equations driven with variable-order fractional Brownian motion. Chaos, Solitons Fractals. 2019;124:105–124. [Google Scholar]
- 31.Ji-jun P., Mahmoudi M.R., Baleanu D., Maleki M. On comparing and classifying several independent linear and non-linear regression models with symmetric errors. Symmetry. 2019;11(6):820. [Google Scholar]
- 32.Mahmoudi M.R., Heydari M.H., Avazzadeh Z. Testing the difference between spectral densities of two independent periodically correlated (cyclostationary) time series models. Commun Stat Theory Methods. 2019;48(9):2320–2328. [Google Scholar]
- 33.Mahmoudi M.R., Heydari M.H., Roohi R. A new method to compare the spectral densities of two independent periodically correlated time series. Math Comput Simulat. 2019;160:103–110. [Google Scholar]
- 34.Mahmoudi M.R., Nasirzadeh R., Mohammadi M. On the ratio of two independent skewnesses. Commun Stat-Theor Methods. 2019;48(7):1721–1727. [Google Scholar]
- 35.Mahmoudi M.R., Heydari M.H., Pho K.H. Fuzzy clustering to classify several regression models with fractional Brownian motion errors. Alexandria Eng J. 2020;59(4):2811–2818. [Google Scholar]
- 36.Mahmoudi M.R., Baleanu D., Tuan B.A., Pho K.H. A novel method to detect almost cyclostationary structure. Alexandria Eng J. 2020;59(4):2339–2346. [Google Scholar]
- 37.Zhou R, Mahmoudi MR, Mohammed SNQ, Pho KH. Testing the equality of the spectral densities of several uncorrelated almost cyclostationary processes. Alexandria Eng J 2020 [Article in Press].
- 38.Mahmoudi M.R., Maleki M., Borodin K., Pho K.H., Baleanu D. On comparing and clustering the spectral densities of several almost cyclostationary processes. Alexandria Eng J. 2020;59(4):2555–2565. [Google Scholar]
- 39.Mahmoudi M.R., Heydari M.H., Avazzadeh Z., Pho K.H. Goodness of fit test for almost cyclostationary processes. Digital Signal Process. 2020;96 [Google Scholar]
- 40.Mahmoudi M.R., Baleanu D., Mansor Z., Tuan B.A., Pho K.H. Fuzzy clustering method to compare the spread rate of Covid-19 in the high risks countries. Chaos Solitons Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Maleki M., Mahmoudi M.R., Heydari M.H., Pho K.H. Modeling and forecasting the spread and death rate of coronavirus (COVID-19) in the world using time series models. Chaos Solitons Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Maleki M., Mahmoudi M.R., Wraith D., Pho K.H. Time series modelling to forecast the confirmed and recovered cases of COVID-19. Travel Med Infect Dis. 2020;101742 doi: 10.1016/j.tmaid.2020.101742. [DOI] [PubMed] [Google Scholar]
- 43.Mahmoudi M.R., Heydari M.H., Qasem S.N., Mosavi A., Band S.S. Principal component analysis to study the relations between the spread rates of COVID-19 in high risks countries. Alexandria Eng J. 2021;60(1):457–464. [Google Scholar]
- 44.Salehi M., Arashi M., Bekker A., Ferreira J., Chen D.G., Esmaeili F. A synergetic R-shiny portal for modeling and tracking of COVID-19 data. Front Public Health. 2021;8 doi: 10.3389/fpubh.2020.623624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Johnson R.A., Wichern D. John Wiley & Sons; Ltd: 2002. Multivariate Analysis. [Google Scholar]