Factor analysis approach to classify COVID-19 datasets in several regions

Abstract

The aim of this research is to investigate the relationships between the counts of cases with Covid-19 and the deaths due to it in seven countries that are severely affected from this pandemic disease. First, the Pearson’s correlation is used to determine the relationships among these countries. Then, the factor analysis is applied to categorize these countries based on their relationships.

Introduction

In the winter months of 2019–2020, another type of coronavirus, Covid-19, has been reported in Wuhan [1]. This virus has severe destructive effects on the respiratory system. From January to now (April 18, 2020), this epidemic has become epidemic all over the world and day by day the cases with Covid-19 and the deaths due to Covid-19 are extremely increasing in most of countries [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15]. There are many techniques analyze the natural phenomena including artificial intelligence, mathematical and statistical methods such as optimization, deep learning, time series analysis, machine learning, regression modeling, clustering and numerical analysis [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39]. Since Covid-19 has many impacts on environment, health, society and economy, the study of the rate of spread of this disease and the comparison of its rate in different countries is essential. There are some researches about the classification of Covid-19 datasets [40], [41], [42], [43]. These researches are based on time series analysis, principal component analysis and fuzzy clustering.

The aim of this research is to study the relationships between the counts of the cases with Covid-19 and the deaths due to it in seven countries that are severely affected from this pandemic disease. First, the coefficients of correlation are computed to determine the relationships between these countries. Then, the factor analysis is applied to categorize these countries using the counts of cases and deaths.

Material and method

This section is devoted to study the research’s dataset and to and to introduce the factor analysis.

Dataset

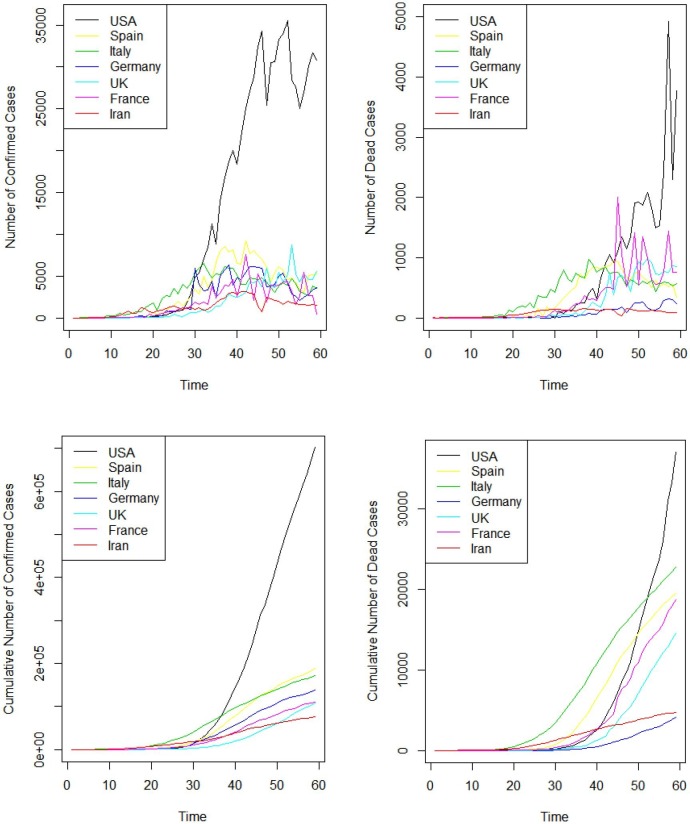
In this work, the counts of the cases with Covid-19 and the deaths due to it in United States America, United Kingdom, Spain, Italy, Iran, Germany, and France from February 22 to April 18 of 2020, are considered [43], [44]. Table 1 summarizes the descriptive statistics of dataset containing the mean and the standard deviation. It can be observed that Iran and United States America have the minimum and the maximum counts of the cases with Covid-19. In addition, Germany and United States America have the minimum and the maximum of the deaths due to Covid-19. The plots for the counts of the cases with Covid-19 and the deaths due to it are also demonstrated in Fig. 1 .

Table 1.

The mean and standard deviation for the counts of the cases with Covid-19 and the deaths due to this pandemic disease.

	Country	Mean ± Standard Deviation
Cases	United States America	11900.8 ± 13327.5
	Spain	3187.6 ± 3016.8
	Italy	2922.6 ± 2056.1
	Germany	2329.2 ± 2245.2
	France	1851.5 ± 1876.0
	United Kingdom	1842.1 ± 2207.7
	Iran	1294.5 ± 921.5
Deaths	United States America	628.0 ± 1013.4
	Italy	385.5 ± 309.5
	Spain	330.1 ± 340.5
	France	316.6 ± 447.3
	United Kingdom	247.1 ± 342.0
	Iran	80.7 ± 55.6
	Germany	69.7 ± 94.9

Fig. 1.

Counts of the cases (Left side of Top), counts of the deaths (Right side of Top), cumulative counts of the cases (Left side of Bottom), and cumulative counts of the deaths (Right side of Bottom).

The relationships between the rates of the spread of Covid-19 among these countries have been studied using Pearson’s coefficient of correlation. As it can be seen in Table 2 , all of the values are more than 0.5 and significant, and consequently there are strong positive relationships between the rates of spread of Covid-19 in all of countries.

Table 2.

Pearson’s coefficient of correlation between the rates of spread of Covid-19.

		United States America	Spain	Italy	Germany	United Kingdom	France	Iran
Patients	France	1	0.586	0.850	0.766	0.851	0.856	0.673
	Germany	0.586	1	0.654	0.514	0.562	0.550	0.942
	Iran	0.850	0.654	1	0.848	0.884	0.866	0.718
	Italy	0.766	0.514	0.848	1	0.842	0.879	0.567
	Spain	0.851	0.562	0.884	0.842	1	0.929	0.666
	United Kingdom	0.856	0.550	0.866	0.879	0.929	1	0.654
	United States America	0.673	0.942	0.718	0.567	0.666	0.654	1
Deaths	France	1	0.802	0.621	0.677	0.815	0.804	0.716
	Germany	0.802	1	0.565	0.629	0.764	0.927	0.885
	Iran	0.621	0.565	1	0.934	0.794	0.555	0.449
	Italy	0.677	0.629	0.934	1	0.892	0.626	0.508
	Spain	0.815	0.764	0.794	0.892	1	0.743	0.627
	United Kingdom	0.804	0.927	0.555	0.626	0.743	1	0.889
	United States America	0.716	0.885	0.449	0.508	0.627	0.889	1

* p-value < 0.001.

Principles of factor analysis

Factor analysis (FA) as a popular multivariate statistical technique transforms some dependent features into some other features called factors such that the first factors of this transformation have the main information of the first dataset [45]. In other words, FA is used to convert a dataset with high dimensions to a dataset with lower dimensions, by considering minimum factors such that the dimension of the converted dataset is decreased. FA focuses on the correlations of variables such that the variables in a factor are highly correlated with each other and the variables in different factors are highly uncorrelated with each other. In applications, the number of the main factors in FA is usually considered as the number of the eigen-values of the correlation’s matrix with the values larger than one. To investigate the suitability of FA, the Kaiser-Meyer-Olkin (KMO) index is used. The KMO greater than 0.8 verifies the accuracy of FA.

Assume $\mathit{X}={\left(X_1,\cdots ,X_p\right)}^T$ is a random vector. Denote

$$\mathit{\mu }=E\left(\mathit{X}\right)={\left({\mu }_1,\cdots ,{\mu }_p\right)}^T$$

and

$$\mathrm{\Sigma }=Var\left(\mathit{X}\right)=\left[\begin{array}{ccc}{\sigma }_{11}& \cdots & {\sigma }_{1p}\\ \cdots & \cdots & ...\\ {\sigma }_{p1}& \cdots & {\sigma }_{\mathit{pp}}\end{array}\right]$$

as the mean vector and covariance matrix of $\mathit{X}$ .

The equation of factor analysis with m factors ($m\le p$) is presented by

$$\mathit{X}-\mathit{\mu }=L\mathit{F}+\mathit{\epsilon },$$

such that

$$\mathrm{L}=\left[\begin{array}{ccc}{l}_{11}& \cdots & l_{1m}\\ \cdots & \cdots & ...\\ l_{p1}& \cdots & l_{\mathit{pm}}\end{array}\right],$$

$$\mathit{F}={\left(F_1,\cdots ,F_m\right)}^T,$$

and

$$\mathit{\epsilon }={\left({\epsilon }_1,\cdots ,{\epsilon }_p\right)}^T.$$

The matrix $\mathrm{L}$ and the vectors $\mathit{F}$ and $\mathrm{\Psi }$ are called the factor loading matrix, the factors and errors, respectively.

This model can be rewritten by

$$X_i-{\mu }_i=\sum _{j=1}^m{l}_{\mathit{ij}}{F}_j+{\epsilon }_i,i=1,\cdots .,p,$$

such that $l_{\mathit{ij}}$ is named as the loading of $X_i$ on the factor $F_j.$

In orthogonal factor analysis, we have

$$Cov\left(\mathit{X},\mathit{F}\right)=L,$$

and

$$\mathrm{\Sigma }=\mathrm{L}{\mathrm{L}}^T+\mathrm{\Psi },$$

where

$$\mathrm{\Psi }=Var\left(\mathit{\epsilon }\right).$$

Consequently,

$$Var\left(X_i\right)=\sum _{j=1}^m{l}_{\mathit{ij}}^2+{\mathrm{\Psi }}_i,$$

and

$$Cov\left(X_i,X_j\right)=\sum _{k=1}^m{l}_{\mathit{ik}}{l}_{\mathit{jk}}.$$

${\sum }_{j=1}^m{l}_{\mathit{ij}}^2$ is determines the proportion of $Var\left(X_i\right)$ that can be explained by the factors $F_1$, …, $F_m.$

The main aim of factor analysis is to find the values of the loadings. To compute the matrices $L$ and $\mathrm{\Psi }$, different approaches such as principal component and maximum likelihood can be applied. Principal component approach uses eigen-values and eigen-vectors to decompose the matrix $\mathrm{\Sigma }$ to find the matrix L. Maximum likelihood approach computes the likelihood and then optimize it to find the matrices $L$ and $\mathrm{\Psi }.$

When the loading values are estimated, we can consider loading plots. Loading plots can be used to

• ⁶Study the correlations between variables
• ⁶Categorize and Classify the variables
• ⁶Detect the number of factors

In loading plot, the angle between two variables ($\theta$) determines the correlation ($r$) between them. $\theta$ = 90° verifies that two variables are uncorrelated ($r=0)$. The cases $\theta$ = 0° and $\theta$ = 180° refer to exact positive and negative linear relationship, respectively.

Results

This section reports the results of FA approach to classify the countries based on research’s variables. It should be noted that the number of the main factors in FA was considered as the number of the eigen-values of the correlation’s matrix with the values larger than one. Moreover, the KMO values were more than 0.8 that verify the accuracy of FA approach.

Counts of cases with Covid-19

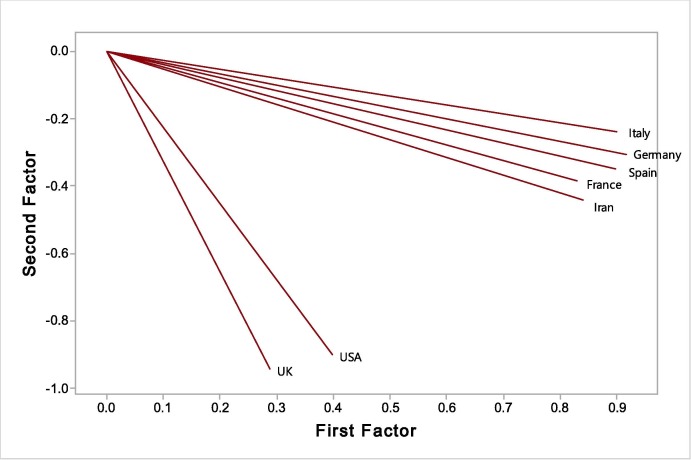
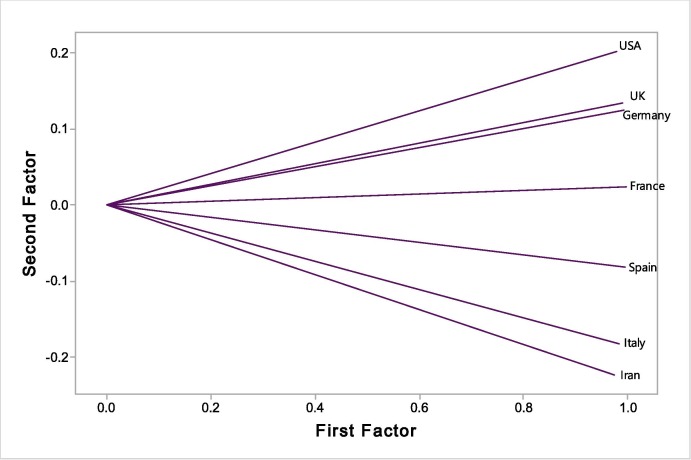
The results of FA technique to categorize the research countries, in basis of the counts of the cases with Covid-19, are provided in Fig. 2 . The outputs demonstrate the statistical differences between the relationships among the countries and we can categorize the countries into following classes:

Fig. 2.

FA technique to categorize the countries in basis of the counts of the cases with Covid-19.

First class: Iran, France, Spain, Germany, Italy.

Second class: United Kingdom, United States America.

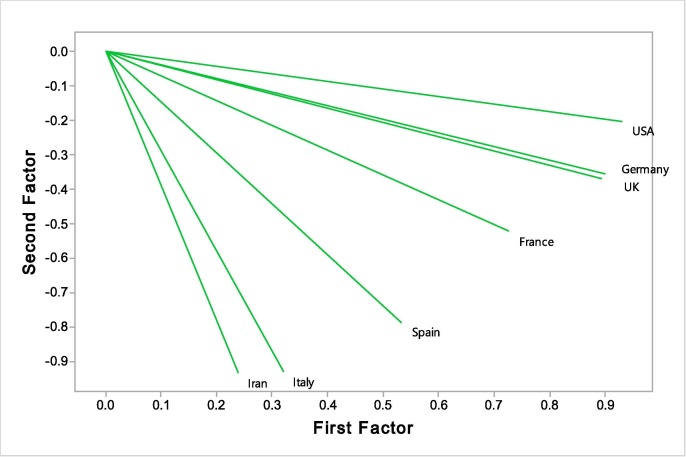
Counts of the deaths due to Covid-19

The results of FA technique to categorize the research countries, in basis of the counts of the deaths due to Covid-19, are provided in Fig. 3 . The outputs demonstrate the statistical differences between the relationships among the countries and we can categorize the countries into following classes:

Fig. 3.

FA technique to categorize the countries in basis of the counts of the deaths due to Covid-19.

First class: France, United Kingdom, Germany and United States America.

Second class: Iran, Italy and Spain.

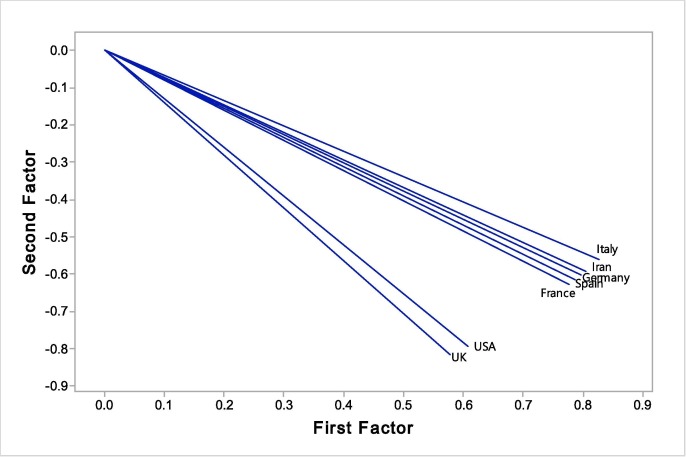
Cumulative counts of the cases with Covid-19

The results of FA technique to categorize the research countries, in basis of the cumulative counts of the cases with Covid-19, are provided in Fig. 4 . The outputs demonstrate the statistical differences between the relationships among the countries and we can categorize the countries into following classes:

Fig. 4.

FA technique to categorize the countries in basis of the cumulative counts of the cases with Covid-19.

First class: France, Spain, Germany, Iran and Italy.

Second class: United Kingdom and United States America.

Cumulative counts of the deaths due to Covid-19

The results of FA technique to categorize the research countries, in basis of the cumulative counts of the deaths due to Covid-19, are provided in Fig. 5 . The outputs demonstrate the statistical differences between the relationships among the countries and we can categorize the countries into following classes:

Fig. 5.

FA technique to categorize the countries in basis of the cumulative counts of the deaths due to Covid-19.

First class: France, United Kingdom, Germany and United States America.

Second class: Iran, Italy and Spain.

Conclusion

Since Covid-19 has many impacts on environment, health, society and economy, the study of the rate of spread of this disease and the comparison of its rate in different countries is essential. The aim of this research was to study the cases with Covid-19 and the deaths due to this pandemic disease in seven countries that are severely affected from this pandemic disease. The cases and the deaths in United States America, United Kingdom, Spain, Italy, Iran, Germany, and France from February 22 to April 18 of 2020, were considered. First, the coefficients of correlation were computed to determine the relationships among these countries. The outputs showed that there were strong positive relationships between the rates of spread in all of countries. Then, the factor analysis was applied to categorize the countries in basis of the counts and deaths. For the cases with Covid-19, United Kingdom and United States America were similarly distributed to each other and were differently distributed from other countries. Also, for the deaths, Iran, Italy and Spain were similarly distributed to each other and were differently distributed from other countries. For future works, the authors suggest classifying the Covid-19 datasets of more regions based on FA technique, or apply this technique to classify the regions for other epidemic or pandemic diseases.

CRediT authorship contribution statement

Mohammad Reza Mahmoudi: Conceptualization, Investigation, Data curation, Validation, Methodology, Software, Writing - original draft. Dumitru Baleanu: Conceptualization, Supervision, Visualization, Writing - review editing. Shahab S. Band: Validation, Visualization, Software, Writing - review editing. Amir Mosavi: Visualization, Writing - review editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.