Time resolved speckle contrast optical spectroscopy at quasi-null source-detector separation for non-invasive measurement of microvascular blood flow

Abstract

Time (or path length) resolved speckle contrast optical spectroscopy (TD-SCOS) at quasi-null (2.85 mm) source-detector separation was developed and demonstrated. The method was illustrated by in vivo studies on the forearm muscle of an adult subject. The results have shown that selecting longer photon path lengths results in higher hyperemic blood flow change and a faster return to baseline by a factor of two after arterial cuff occlusion when compared to SCOS without time resolution. This indicates higher sensitivity to the deeper muscle tissue. In the long run, this approach may allow the use of simpler and cheaper detector arrays compared to time resolved diffuse correlation spectroscopy that are based on readily available technologies. Hence, TD-SCOS may increase the performance and decrease cost of devices for continuous non-invasive, deep tissue blood flow monitoring.

1. Introduction

The continuous, real-time assessment of local, deep (>1 cm) microvascular blood flow is, in general, desirable for monitoring both healthy and pathological tissue function. However, no such accepted clinical modality exists that does not require complex imaging facilities, patient transport and does not rely on indirect, surrogate measurements.

Diffuse optical methods utilizing near-infrared (∼650-950 nm) light such as diffuse correlation spectroscopy (DCS) [1] have been emerging as potential candidates to fill this gap. DCS has been demonstrated for several promising applications and its use is spreading [2–4]. However, as all diffuse optical techniques, DCS suffers from significant limitations due to partial volume effects stemming from tissue heterogeneity [5]. For example, when measuring the adult human brain, the photons have to propagate through about a centimeter of overlying tissue whose blood flow values, and their changes should be separated from those of the cerebral cortex.

Time (or photon path length) resolved diffuse optical methods are currently the most promising approaches for achieving this goal by measuring the distribution of detected photons according to the time, i.e. path length, spent in the probed tissue volume [6,7]. By using this method, researchers have been able to demonstrate improved accuracy and precision [8], enhanced depth sensitivity and selectivity [9]. An promising recent approach to this method is the use of quasi-null or null source-detector separation [10–13]. This method allows the researchers to avoid the traditional use of increased distance between the source and the detection points to optimize the mean penetration depth. The quasi-null source-detector separation method requires the use of gated detection, where the “blinding” (or saturation) of photodetectors is avoided by turning the detectors ON/OFF (synchronously with the laser pulses) rapidly (with a transient time of hundreds of picoseconds) for a duration of few nanoseconds. Under this hardware gated modality, late – i.e. deep – photons can be gathered in larger abundance as compared to the traditional larger source-detector distance scheme [13]. Furthermore, the traditional approach leads to bulkier tissue probes whereas the quasi-null source-detector separation, by design, uses smaller probes.

It is more complex to translate this approach to DCS measurements, and, to that end, in vivo time domain DCS (TD-DCS) has emerged as a potential method to introduce path length resolution to blood flow measurements. In principle, TD-DCS can enhance the depth sensitivity and selectivity of DCS, thus, reducing the partial volume effects [14–16]. In a previous study, our group has demonstrated TD-DCS at a quasi-null (few millimeters) source-detector separation using fast-gated single-photon avalanche diodes (fgSPADs) [17].

While these results have been promising, TD-DCS suffers, as DCS, from the limited light available when detecting a single laser speckle. The small area of the diffused laser speckles requires photon detection from an equally small area. This has been studied in detail, and the use of parallel detection of multiple speckles was identified to be the current best approach to improve the signal-to-noise ratio (SNR) in DCS [18–20]. We note that SNR scales by the square root [19,20] of the number of detected speckles which makes the method unwieldly expensive and limits its portability, although experiments using up to thirty-two detectors in parallel have been proposed [21]. Time domain DCS is even more photon starved since only a small fraction of the detected photons come from the path lengths of interest. Furthermore, the high readout speed needed for every detector makes the electronics for each detection channel more complex and expensive.

On the other hand, speckle contrast optical spectroscopy (SCOS) uses a different data type which is essentially a weighed integral of the intensity auto-correlation function that DCS uses. As such, SCOS was shown to be more scalable by enabling the use of slower and/or cheaper detector arrays like megapixel cameras [22]. In fact, recently, SCOS and its tomographic analogue, speckle contrast optical tomography (SCOT), have been shown to be able to obtain high SNR data from the rodent [23,24] and adult human brain including the demonstration of a potential wearable, low-cost system [25]. Other groups have implemented SCOS/SCOT using different terminology with similar results extending its use to other applications [26–30].

In this work, we have carried out a proof-of-concept study introducing quasi-null separation time domain SCOS (TD-SCOS) as a path length resolved, deep tissue monitoring technique analogous to TD-DCS. We describe the instrumentation, demonstrate its feasibility by in vivo measurements and speculate about a future relatively simpler and low-cost TD-SCOS system.

2. Materials and methods

2.1. Theory: time domain speckle contrast optical spectroscopy

Photons traverse tissue undergoing multiple scattering. Each path of a single photon can be characterized by its length ($s$) or, equivalently, its time-of-flight $(t)$. If coherent light is used it is possible, by measuring the intensity or field statistics of one or multiple speckles in time and/or space (which are equivalent for an ergodic medium [31]), to derive information about the movement of the scatterers and, therefore, to quantify bulk blood flow since the motion of the red blood cells dominate the scatterer motion in tissues [1,2]. In traditional DCS, this is done by computing the normalized autocorrelation function $(g_2)$ of the intensity recorded by single-photon counting detectors. This quantity is related, under certain assumptions, to the normalized electric-field autocorrelation $(g_1)$ by the Siegert relation [32] as

$$g_2(\tau )=1+\beta |g_1(\tau ){|}^2$$ (1)

where $\tau ([s])$ is the correlation lag time and $\beta \equiv g_2(0)-1$ is a non-dimensional parameter (the so-called coherence factor) that increases with the SNR of the measured blood flow and that depends on the experimental conditions. For example, it decreases with the number of speckles detected at the same time by a single detector.

As mentioned above, in order to optimize the detection process, often each detector is coupled to a single speckle by using single mode fibers [33]. When a multimode mode fiber is used to couple multiple speckles to a single detector [34] a lower $\beta$ counterbalances a higher count rate, nullifying most of the gains in SNR. The SNR can be increased by using several detection channels in parallel, at the expense of cost and complexity of the instrumentation.

In SCOS and SCOT the statistical properties of the fluctuating speckle pattern are measured by the ratio of the variance $({\sigma }_I^2$) over the mean square ($I^2$) of the detected intensity of independent speckles. This is often computed for a set of integration times ($T$). This quantity is termed squared speckle contrast (${\kappa }^2$) and can be calculated in the temporal or spatial domain i.e., the statistics are evaluated either from multiple speckles measured simultaneously (spatial domain) or from a single speckle measured over time (temporal domain). For polarized light, its value varies between zero and one with higher values indicating slower fluctuations of the scatterers and it can be related to the normalized electric field autocorrelation function by [35,36]:

$${\kappa }^2(T)=\frac{{\sigma }_I^2}{⟨I{⟩}^2}=\frac{2\beta }{T}{\int }_0^T\left(1-\frac{\tau }{T}\right)|g_1(\tau ){|}^{2}d\tau$$ (2)

Typically, the integration time is in the order of several hundred micro-seconds which allows for the use of slower and generally less performant detectors with respect to the ones used in DCS. Even standard digital cameras are usable. This has allowed for the parallelization of detection (i.e., over different pixels), therefore improving the SNR. The use of two-dimensional arrays as also allowed researchers to simultaneously measure multiple source-detector separations for tomographic approaches.

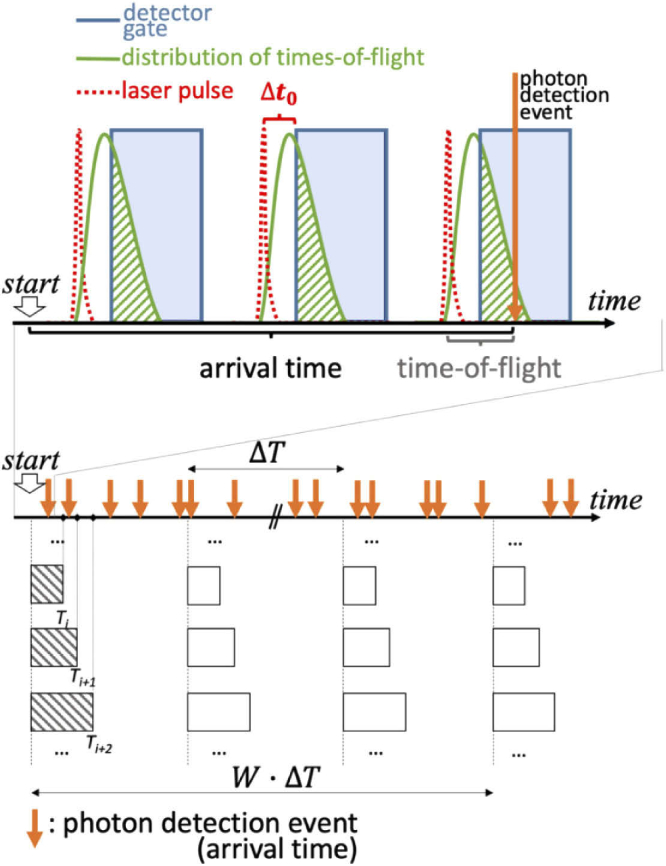
In order to explain our implementation of TD-DCS and TD-SCOS, we illustrate key temporal quantities in Fig. 1. In case of TD-DCS [14–16], the photon path length ($s=vt,[cm]$) in the tissue is resolved. For a homogeneous index of refraction, the path length is related to the speed of light in the tissue as $v=c/n$, where n is the refractive index of the medium and c is the speed of light in vacuum. The autocorrelation of the electric field for a single path can be modeled as [37]:

$$g_1^{(1)}(\tau ,s)=exp\left[-2{\mu }_s^{\prime }{\left(\frac{2\pi n}{\lambda }\right)}^{2}BFis\tau \right],$$ (3)

where ${\mu }_s^{\prime }$ ([cm^-1]) is the reduced scattering coefficient of the sample and $\lambda$ ([cm]) is the wavelength of the source in vacuum, while BFi ([cm²/s]) is the Brownian diffusion coefficient of the scatterers, termed blood flow index for biomedical tissues. If instead, there is a small set of path lengths, $[s_A,s_B]$ (or, equivalently, a time gate $[t_A,t_B]$), within which all photons are gathered, the gated electric field autocorrelation function can be written as [15,17,38]

$$g_1(\tau )={\int }_{S_A}^{S_B}R(s;\rho )g_1^{(1)}(\tau ,s)ds,$$ (4)

where the normalized distribution of photon path length $(R(s;\rho ))$ is the solution for the photon diffusion equation [39,40] that depends on the optical properties of the sample (absorption coefficient ${\mu }_a[c{m}^{-1}]$, ${\mu }_s^{\prime }$ and $n$), the source-detector separation $(\rho [cm])$, and the boundary conditions. We note that if there is no path length resolution, or if continuous wave illumination is utilized as in SCOS and DCS, then $s_A=0$ and $s_B=\mathrm{\infty }$ which reduces to the classical (i.e. CW) models for correlation transport [1,2,19,22].

Fig. 1.

A schematic representation of the arrival time and time-of-flight associated to a photon detection event during the gated detection process. Detection is possible only where time resolved probabilities of laser light injection (red dashed line) and consequent re-emission by the tissue at a certain distance (green continuous line), periodically for each laser pulse, are intersected (green dashed area) with the time gate in which the fgSPAD detector is ON (blue shaded area). The bins that are used to compute ${\kappa }^2$ are reported as rectangles of different durations $T_i$.

At this point, Eq. (2), (3) and (4) can be combined to obtain an expression for the time-gated speckle contrast that can be used to fit the measured square speckle contrast and to obtain BFi in vivo:

$${\kappa }^2(T)=\frac{2\beta }{T}{\int }_0^T\left(1-\frac{\tau }{T}\right){\left|{\int }_{S_A}^{S_B}R(s;\rho )exp\left[-2{\mu }_s^{\prime }{\left(\frac{2\pi n}{\lambda }\right)}^{2}BFis\tau \right]ds\right|}^{2}d\tau$$ (5)

The quantity ${\kappa }^2$ can be computed by binning the number of photons detected over a set of integration times ($T$). Bins are repeated periodically with a period $\mathrm{\Delta }T$, which is chosen as equal to or greater than the typical $g_2$ decorrelation time (${\tau }_c,$) to ensure independent counts. The standard deviation and the mean are then computed, for each T separately, among the number of binned counts that fall within a window of duration $W\cdot \mathrm{\Delta }T$, which gives the temporal period of the SCOS measurement.

2.2. Experimental set-up

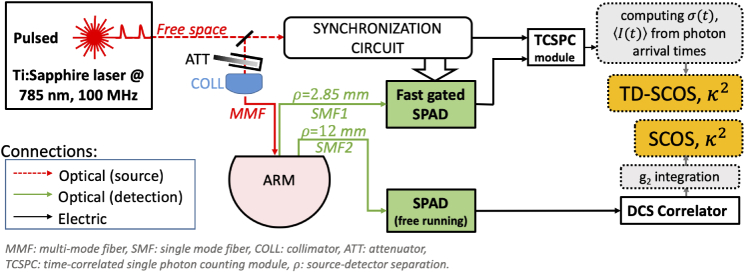
The TD-SCOS setup was developed on the same time gating strategy that was previously used in TD-DCS at a quasi-null separation [17]. Figure 2 shows a schematic diagram of the experimental setup. The system is described in detail in Ref. [15,41]. The laser source was a custom-made active mode locked titanium-sapphire laser (Ti:Sa) operated at a central wavelength of $\lambda$ = 785 nm and coupled to a 3 m long, 200 µm core diameter step index fiber (WF200, Ceramoptec, USA). The laser temporal coherence was evaluated, by using methods similar to Ref. [16] to be approximately 200 ps. This value is slightly lower than the pulse full-width at half-maximum (300 ps). To ensure tissue safety, the laser power on the tip of the injection fiber was limited to <30 mW, using a circular attenuator.

Fig. 2.

Schematics of the experimental setup. White and green blocks with continuous contour represent hardware components; grey blocks with dashed contour line refer to computational processes that are carried on a personal computer; in yellow blocks, datatypes of interest.

On the detector side, two single mode fibers (780HP, 4.4 µm core diameter, cutoff wavelength 730 nm, Nufern, USA) collected light from the sample. One was placed at 12 mm from the source and the other at a quasi-null source-detector separation of 2.85 mm. The latter was the smallest source-detector separation allowed by the physical dimension of the ferrules of the two fibers.

For the 12 mm separation, the single mode fiber was coupled to a free-running (i.e., not gated) SPAD detector (PDM, Micro Photon Devices, Italy). A hardware correlator (Correlator.com, USA) computed the autocorrelation of the generated signal every 2 s. This channel was used as a monitor and a standard SCOS analysis was carried out on the intensity autocorrelation curves. In other words, this channel implemented the equivalent of a continuous-wave DCS/SCOS experiment and was used as a monitor.

For the quasi-null (2.85 mm) source-detector separation, the single mode fiber was coupled to a fgSPAD which was developed in house [42]. The fgSPAD gate was open for 4 ns at each laser cycle with a $\mathrm{\Delta }{t}_0$ = 512 ps delay with respect to the laser pulse peak. Its output was connected to a time-correlated single-photon counting (TCSPC) module (PH300, Picoquant, Germany).

For each photon detected from the fgSPAD at quasi-null source-detector separation, the time-of-flight was computed as the difference between detection time and the peak of the previous laser pulse. Briefly, each detected photon had to have a time-of-flight greater or equal to the gating delay time, $\mathrm{\Delta }{t}_0$ = 512 ps, that was set for the detector, and smaller than $\mathrm{\Delta }{t}_0$ + 4 ns, which was the duration of the gate. For each detected photon, the arrival time was recorded by the TCSPC module.

2.3. Data analysis

The optical properties (${\mu }_a$ and ${\mu }_s^{\prime }$) were measured in a separate time resolved reflectance spectroscopy (TRS) experiment [9] which used the same source and a free-running detector at a 12 mm separation on the same location on the arm of the same subject. These properties have been used for computing the solution of the diffusion equation, $R(t=s/v)$, using a homogeneous, semi-infinite model with the extrapolated boundary conditions at both source-detector pairs of the TD-SCOS experiment [44]. Equation (4) was then evaluated numerically at 10 ps steps using the computed values.

For the TD-SCOS channel, ${\kappa }^2$ was computed over a set of exposure times ($T_j$ with $j$ = 1…$m$ of $m$ = 20 integration times: $T_j$ = 50, 100, 200 µs to 2 ms (spaced 200 µs), and 3 to 10 ms (spaced 1 ms). The computation of ${\kappa }^2(T)$ was carried out over a 5 s ($\mathrm{\Delta }T$=10 ms, $W$=5000) temporal window. The window was then shifted by one second (delay $d$ = 1 s) and another set of ${\kappa }^2(T)$ was obtained until the whole time span of the experiment was covered. The integral expression for the speckle contrast (Eq. (5)) was numerically solved for each integration time using the computed diffuse reflectance . The model was then fitted to the measured ${\kappa }^2(T)$ obtained for each data point and, in so doing, BFi and $\beta$ were determined as the best-fit parameters. This algorithm is an adaptation, to TD-SCOS, of the spatial window SCOS algorithm [19] and implements the Poisson noise correction as described in Ref. [22].

For the monitor SCOS channel, the ungated intensity autocorrelation function $g_2(\tau )$ was computed every two seconds by the hardware correlator. At this source-detector separation, ${\kappa }^2(T)$ were obtained by numerically estimating Eq. (2) with $g_2(\tau )$ as an input for the same set of $T_j$ used for TD-SCOS. ${\kappa }^2(T)$ and the estimated $\beta$ from the corresponding $g_2(\tau )$ curve were fitted to analytical model for standard SCOS [22] to obtain BFi.

The Nelder-Mead simplex method was used to fit measured ${\kappa }^2$ in both the SCOS and TD-SCOS detection channels using the “fminsearch” function in MATLAB (MathWorks, USA).

2.4. Protocol and human subject preparation

An adult subject (female, 26 years old) underwent a common arterial cuff occlusion protocol of the upper arm consisting in three minutes of baseline, three minutes of arterial occlusion and four minutes of recovery. The entire protocol lasted 600 s. While the subject sat comfortably on a chair with the elbow bent and the forearm resting on a tablecloth, arterial circulation was stopped by rapidly inflating the tourniquet of a manually operated sphygmomanometer placed on the arm at the height of the biceps to 180 mmHg. The inflated tourniquet pressure was well above subject´s systolic pressure. A 3 × 3 cm² soft black foam pad probe embedding the source and detector fibers was placed above the brachioradialis muscle of the same arm. The superficial tissue thickness in the region of the probe was estimated to be 13 mm using a skin caliper. The protocol was approved by the Ethical Committee of Politecnico di Milano and was conducted in agreement with the Declaration of Helsinki. The subject gave written consent before participation.

3. Results

First, the overall optical parameters are reported. The count rate was, on average, 396 ± 18 kcps for the quasi-null separation TD-SCOS channel (average $\beta$ = 0.26) and 242 ± 20 kcps for the 12 mm separation SCOS channel (average $\beta$ = 0.21). The results of the TRS experiment on the arm, carried out immediately before the beginning of the cuff occlusion protocol, were ${\mu }_s^{\prime }$ = 10.3 cm⁻¹ and ${\mu }_a$ = 0.14 cm⁻¹. We were able to obtain good SNR data by all modalities.

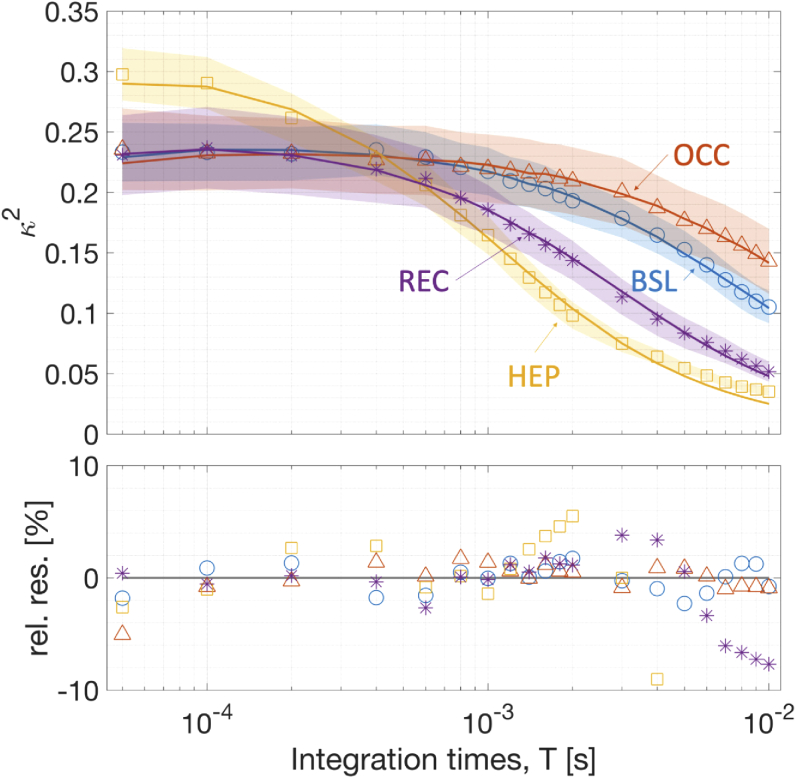
Figure 3 shows the computed time-gated speckle contrast from the quasi-null source-detector separation alongside the curves fitted by the physical model. Bottom panel shows the percent residuals between the fit and the data. The decay with respect to the integration time T is fitted well by the physical model. When compared to the baseline (first 100 s) the decay rates of ${\kappa }^2(T)$ were reduced during the occlusion and were increased during hyperemic peak (reperfusion) which is expected after releasing the cuff occlusion. In every case, the intensity autocorrelation decay time was smaller than 10 ms.

Fig. 3.

On top, representative speckle contrast curves measured by TD-SCOS at quasi-null separation are shown. Continuous lines represent the best fit according to the physical model. Four curves have been chosen at different times from the start of the protocol (in parenthesis) to represent baseline (40 s, BSL: blue ○), occlusion (209 s, OCC: orange △), hyperemic peak (392 s, HEP: yellow □) and recovery (603 s, REC: purple *) epochs. Shaded areas represent the standard deviation of ${\kappa }^2$ during the epoch. On the bottom, the percentage relative residuals (rel. res.; fitted minus measured ${\kappa }^2$) are reported.

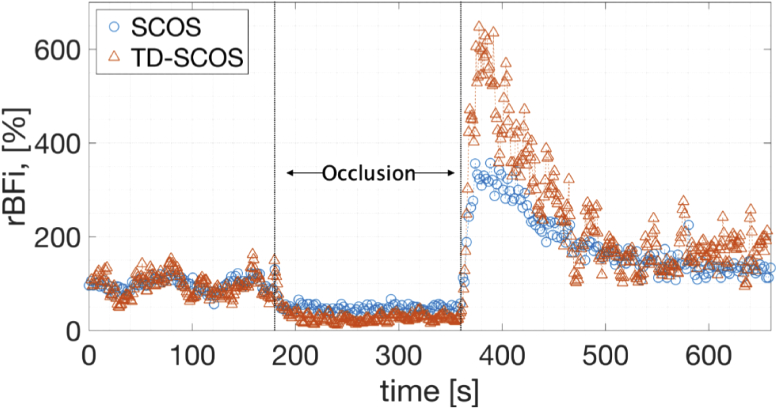
Figure 4 shows the time-series of the relative BFi (rBFi, [%]) i.e., the BFi normalized by division to the initial baseline period of 100 s (chosen to exclude any contamination from the period during which the cuff inflation was starting) and multiplied by hundred, for both the TD-SCOS at quasi-null separation and the CW-equivalent SCOS measurement at 12 mm separation. The measured rBFi varied as expected during the occlusion protocol for both curves.

Fig. 4.

Relative BFi (rBFI) measured with SCOS method (blue ○) and with TD-SCOS at quasi-null source-detector separation with temporal gating starting at Δt = 512 ps (orange △) before, during and after arterial cuff occlusion. The occlusion was performed from second 180 to second 360 by inflating a torniquet to 180 mmHg pressure.

Relative BFi dropped to an average of 10% of the baseline during the occlusion for both curves. Then, it increased up to 500% and 330% of the baseline for TD-SCOS and SCOS, respectively during the hyperemic peak (380 to 420 s). This marked a (160 ± 120)% higher value for the BFi measured by TD-SCOS at quasi-null separation. By modeling the return of the rBFi back to the baseline after the hyperemic peak, namely from roughly 380 to 500 s, as an exponential, the recovery rate was calculated as -1.5%/s and -0.7%/s for the TD-SCOS and SCOS, respectively. In other words, the measured blood flow index recovered back to the baseline after the release of the cuff about twice as fast in the gated quasi-null separation than in the 12 mm separation channel.

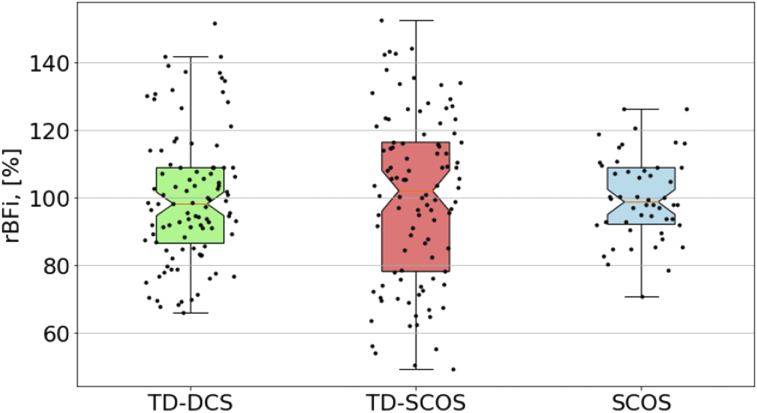
Despite the count rate being substantially (48%) higher, the assessed BFi from TD-SCOS was more prone to experimental noise than SCOS. In order to better characterize the possible causes of this excess noise, we have performed a TD-DCS analysis, as described in [15] at the quasi-null separation. We have computed, on the data from the baseline period (0-100 s), the coefficient of variation (CV) of the rBFi, defined as the standard deviation over the mean. Figure 5 shows the results which correspond to a CV of 0.20, 0.25 and 0.13 for TD-DCS, TD-SCOS and SCOS, respectively.

Fig. 5.

Boxplot (notch: median, colored area marks interquartile range) showing variability of rBFi estimated during the baseline (first 100 s) for the cuff occlusion experiment. Note that SCOS ($\rho$ = 12 mm) data is obtained for an integration time of 2 s, while TD-SCOS and TD-DCS ($\rho$ = 2.85 mm) are obtained by the 5 s sliding window averaging. For each plotted value of rBFi (black dots), spread along the x axis has been added for visualization purposes.

4. Discussion

We have built upon the growing literature on SCOS as a promising, compact, lower-cost method for deep tissue, in vivo measurement of microvascular blood flow and have demonstrated time (or path length) resolved TD-SCOS. An important feature of our work was the utilization of the quasi-null source-detector separation that is enabled by the use of a fast-gated detector. This, in turn, allows for us to envision a measurement where a simple digital or analogue circuit can be utilized to calculate the TD-SCOS datatype with embedded timing electronics.

We have shown quasi-null source-detector separation TD-SCOS to be comparable to quasi-null-separation TD-DCS [17] in SNR and in the estimation of in vivo changes during an arterial arm cuff-occlusion protocol. Since the main aim of this work was to have a proof-of-concept demonstration of the technique, and not to perform a systematic comparison, we have measured a single subject. However, we point out that TD-SCOS has a computationally simpler datatype than the intensity autocorrelation used in TD-DCS, and it imposes a lower data transfer rate burden to the detector and associated electronics. In fact, the computation of the speckle contrast is expected to be simpler and faster than computing the intensity autocorrelation as suggested by previous reports [23,25]. In particular, in future, we expect the integration of the whole computation field-programmable gate arrays that compute speckle contrast from tens of parallel detectors of a two dimensional array, e.g. a SPAD array, in real time [25]. Also, this would enable the use of multi-mode fibers, which may permit to compute the speckle contrast from spatial instead of temporal statistics, increasing significantly the acquisition rate and SNR [44,45].

As expected, because of the ability to select deeper reaching long photon path lengths for analysis we have observed a higher blood flow increase during the hyperemic peak after the cuff was released and a faster return to the baseline. In comparison to the standard measurement, these features are likely to be present since it is often assumed that the muscle tissue is more reactive than the surrounding tissue, in particular, the superficial adipose tissue [46,47].

The quasi-null separation also amplifies this finding: first, because of the higher depth sensitivity and selectivity, and, second, because of the smaller lateral dispersion of the sensitivity area [6,7,12,13,48,49]. In other words, the temporal gating of long time-of-flight photons in quasi-null separation TD-SCOS increases depth sensitivity and selectivity in a way that is similar to having longer source-detector separations in DCS and SCOS. This warrants further investigation with a quantitative analysis of the differences between these methods, for instance by utilizing spatially heterogenous phantoms proposed in other works [15,16,50].

During the cuff occlusion experiment, variations in the rBFi similar to what is reported in Ref. [47] for the larger source-detector separation (30 mm) has been shown demonstrating this point. It is difficult to do justice to the description of an equivalent continuous wave source-detector separation which mimics the chosen 4 ns temporal gate. This has been studied in the past for typical time-domain near-infrared spectroscopy for larger (10 to 15 mm) source-detector separations. These works have demonstrated that the gating approach allows a good contrast for inclusions at a 25 mm depth [48] while the null separation and the gating strategy suggest that inclusions at a 30 mm depth are detectable [7]. However, additional studies are needed for quantifying this aspect in TD-SCOS and TD-DCS.

In diffuse optics, for a limited and constant irradiation power, shorter source-detector separations imply that more photons can be detected at any time-of-flight gate with respect to the case of a larger separation. If a photon diffusion model [43] is used a 4 ns gate with $\mathrm{\Delta }{t}_0$ = 512 ps at 2.85 mm can collect approximately sixty-five times more light compared to an ungated detector at a 30 mm source-detector separation within the same temporal window. This is another supporting point for the benefits of the quasi-null separation TD-SCOS. A thorough comparison requires a proper calibration of the detectors and optics in terms of photon detection efficiency, which has not been carried out.

Fast-gating detectors have been first proposed for diffuse optics in reflectance geometry in order to mitigate the saturation effect at small source-detector separation and therefore increase the dynamic range of diffuse optical measurements [10,51]. Although in this manuscript we have carried out measurements with a single detector, in principle, very dense spatial sampling can be achieved with time-gated detector arrays, like time-gated cameras, which exist as research prototypes [52,53]. In this configuration, by setting the time delay of the temporal gate to reject the surge of small path length, short time of flight photons, all source-detector separation pairs can be utilized since their saturation is avoided The resulting increased freedom in designing the field of view geometry is particularly sought after and is beneficial for tomography [23,48].

To further reduce the cost and the complexity of a TD-SCOS setup, convenient, reliable, and portable laser sources that deliver pulsed, yet sufficiently coherent light are still to be identified. Other groups have reported results with promising technologies such as fiber amplified lasers [16].

Our pragmatic approach in this manuscript to provide a basic proof-of-concept measurement, we argue that there is a real potential to take advantage of this new approach for time-resolved, high SNR, practical technologies for measuring micro-vascular blood flow.

5. Conclusion

In DCS, high SNR is hard to achieve because every detector element collects light from one or few speckles [33,34]. This problem is exacerbated in TD-DCS since the need of precise timing of photon detection event is generally associated with lower detector efficiency and higher cost per detection channel. By using time-gated detectors (and, expectantly, gated detector arrays), and by using the more convenient datatypes and method of analysis such as in SCOS, these drawbacks can be mitigated by averaging the results of multiple adjacent detector elements.

Here we have presented TD-SCOS as a strategy to use single-photon events recorded by fast time-gated detectors that allows to conveniently use multiple detectors in parallel. This has been made possible by decreasing the required readout speed and by reducing the computational complexity, associated to a detector, to a minimum. Photon detection efficiency, in these cases, is generally lower than single SPADs that are optimized for DCS but are comparable with array detectors currently used in SCOS.

In conclusion, we have introduced quasi-null source-detector separation TD-SCOS and demonstrated its feasibility in vivo. We have argued that this approach paves the way for improved time resolved measurements of microvascular blood flow in deep (>1 cm) tissues.

Funding

Laserlab-Europe10.13039/100015668 (LASERLAB-EUROPE V (n. 871124)); Horizon 2020 Framework Programme10.13039/100010661 (n.688303 (LUCA project)); Centres de Recerca de Catalunya10.13039/100015439; Agència de Gestió d'Ajuts Universitaris i de Recerca10.13039/501100003030 (2017 SGR 1380); “Severo Ochoa” Programme for Centres of Excellence in R&D (SEV-2015-0522); “la Caixa” Foundation10.13039/100010434; Ministerio de Economía y Competitividad10.13039/501100003329 (DPI2015-64358-C2-1-R); Instituto de Salud Carlos III10.13039/501100004587 (DTS16/00087); Fundación Cellex10.13039/100008050.

Disclosures

The authors declare that there are no conflicts of interest related to this manuscript. Various authors are holders of relevant patents.