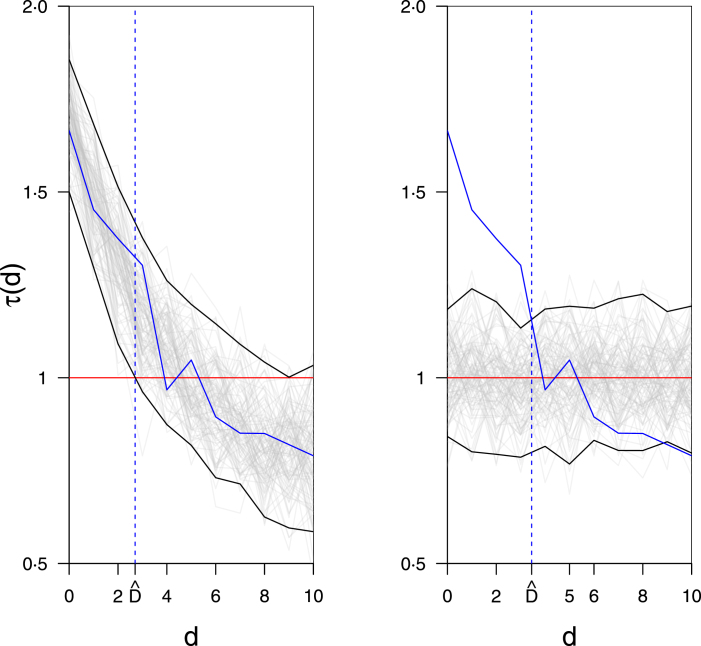
Fig. 2.

Previous naive methods: several authors (Section 3.2) choose one envelope type as ‘central’ (a) or ‘null’ (b), then simultaneously test the hypothesis of no clustering and estimate the clustering endpoint parameter $\hat{D}$ (Pollington et al., 2019a). The single red line $\tau =1$ represents no spatiotemporal clustering nor inhibition. Grey lines indicate (a) a collection of spatial bootstrap estimates ${\hat{\tau }}^{\ast }$ (denoted by ${}^{\ast }$, see Section 3.4.1) from a typical tau estimator characterised by negative exponential lines with Normal noise, or (b) simulations of the tau estimator on time-mark permuted data for null envelope construction, represented here as lines at $\tau =1$ with Normal noise; black lines mark out the envelope bounds constructed from pointwise confidence intervals. The solid blue line characterises an empirical tau point estimate $\hat{\tau }\left(d\right)$.

Instead, we split the method into the separate steps of graphical hypothesis testing (Fig. 4) and point estimation (e.g. Fig. 5) in Sections 3.3 & 3.4, respectively. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)